自復(fù)位部分填充鋼管混凝土橋墩力學(xué)性能研究
王占飛,李夢琦,楊 帆,于豐綸
(1.沈陽建筑大學(xué) 交通與測繪工程學(xué)院 沈陽市 110168; 2.中交綜合規(guī)劃設(shè)計院有限公司 北京市 100024)
0 引言
我國作為橋梁大國,同時也是世界上地震活動最活躍、地震災(zāi)害最大的國家之一,發(fā)展橋梁抗震和減隔震事業(yè)的重要性與必要性不言而喻。目前較為常用的延性抗震設(shè)計方法通過在選定部分形成塑性鉸,耗散地震能量[1]。但該類橋墩在震后會產(chǎn)生不可恢復(fù)的殘余位移,造成交通阻斷和巨大的經(jīng)濟(jì)損失。
近年來,具有自復(fù)位能力的新型橋梁結(jié)構(gòu)憑借損傷可控性、較小的殘余位移及穩(wěn)定的耗能機(jī)制等優(yōu)越的性能,在一眾抗震設(shè)計理念中脫穎而出[2]。搖擺自復(fù)位橋墩與基礎(chǔ)的連接界面進(jìn)行了弱化處理,在地震作用下,允許橋墩提離搖擺,降低了側(cè)向剛度,避免橋墩主體損傷;震后通過橋墩自重與無粘結(jié)預(yù)應(yīng)力鋼絞線實(shí)現(xiàn)復(fù)位,減小了震后的殘余位移。
部分填充鋼管混凝土橋墩由普通鋼橋墩發(fā)展而來,由于鋼管內(nèi)部填充混凝土的支撐作用,橋墩鋼管的局部失穩(wěn)現(xiàn)象得以抑制和延緩,承載力也得到了提高。而填充混凝土則在外部鋼管的約束作用下處于三向受壓的狀態(tài),該受力形式對于提高核心混凝土強(qiáng)度與承載力具有積極作用[3],韌性也可得到改善。此外,混凝土同時參與耗能,進(jìn)一步改善了自復(fù)位橋墩耗能機(jī)制與抗震性能。
目前,自復(fù)位技術(shù)較多應(yīng)用于混凝土墩與鋼桁架,而針對自復(fù)位部分填充鋼管混凝土橋墩的有限元分析和理論研究還有待完善。因此,對自復(fù)位部分填充鋼管混凝土類橋墩進(jìn)行有限元分析,研究設(shè)計參數(shù)對其力學(xué)性能的影響,并提出一種簡易的理論計算方法,為該類橋墩的工程應(yīng)用提供理論依據(jù)。
1 自復(fù)位部分填充鋼管混凝土橋墩
自復(fù)位部分填充鋼管混凝土橋墩高10m,半徑1.1m,由圓形鋼管、填充混凝土、無粘結(jié)后張預(yù)應(yīng)力鋼絞線和鋼隔板構(gòu)成 (如圖1(a)所示)。鋼管為承重組件,用于承受豎向荷載和抵抗橫向荷載;自復(fù)位功能由結(jié)構(gòu)自重與無粘結(jié)后張預(yù)應(yīng)力鋼絞線提供;鋼隔板用于錨固鋼絞線,并在鋼隔板以下填充C50混凝土,填充高度為4m,填充率為40%。核心混凝土作為承重構(gòu)件,同時參與結(jié)構(gòu)耗能。各結(jié)構(gòu)組件各司其職,性能劃分清晰。
為了探究橋墩壁厚t、預(yù)應(yīng)力比α和鋼絞線張拉度T對自復(fù)位部分填充鋼管混凝土橋墩力學(xué)性能的影響,探討了不同設(shè)計參數(shù)下12個部分填充鋼管混凝土橋墩,模型編號及具體參數(shù)如表1所示。預(yù)應(yīng)力比與鋼絞線張拉度的計算公式分別為:
(1)
(2)
式中:σcon、Acon分別為預(yù)應(yīng)力鋼絞線的張拉控制應(yīng)力與截面面積;σys、A0s為鋼管的屈服強(qiáng)度與截面面積;σc、Ac為填充混凝土的單軸抗壓強(qiáng)度與截面面積;σyp為預(yù)應(yīng)力鋼絞線的抗拉強(qiáng)度。
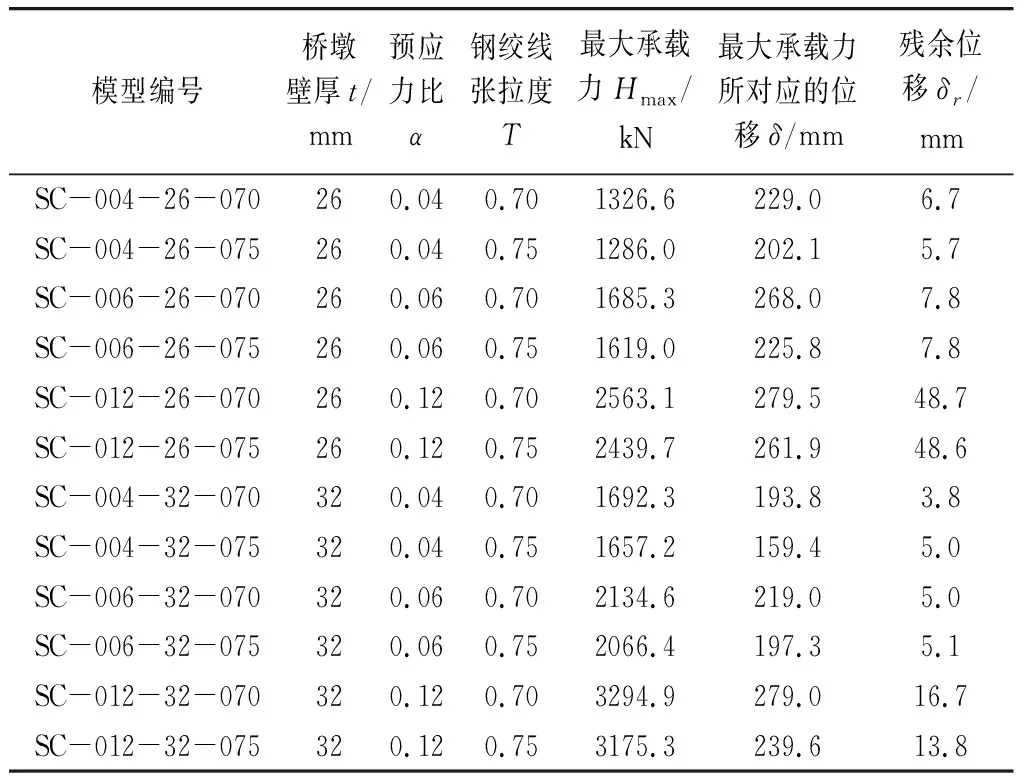
表1 有限元模型及分析結(jié)果
2 有限元分析
2.1 模型建立
采用混合單元的方式建立自復(fù)位部分填充鋼管混凝土橋墩有限元模型。模型如圖1(b)所示:橋墩上部采用梁單元T3D2,下部采用殼單元S4R,填充混凝土、承臺和錨塊采用實(shí)體單元C3D8R,鋼絞線采用桁架單元,對于重點(diǎn)關(guān)注部位進(jìn)行了網(wǎng)格加密處理。
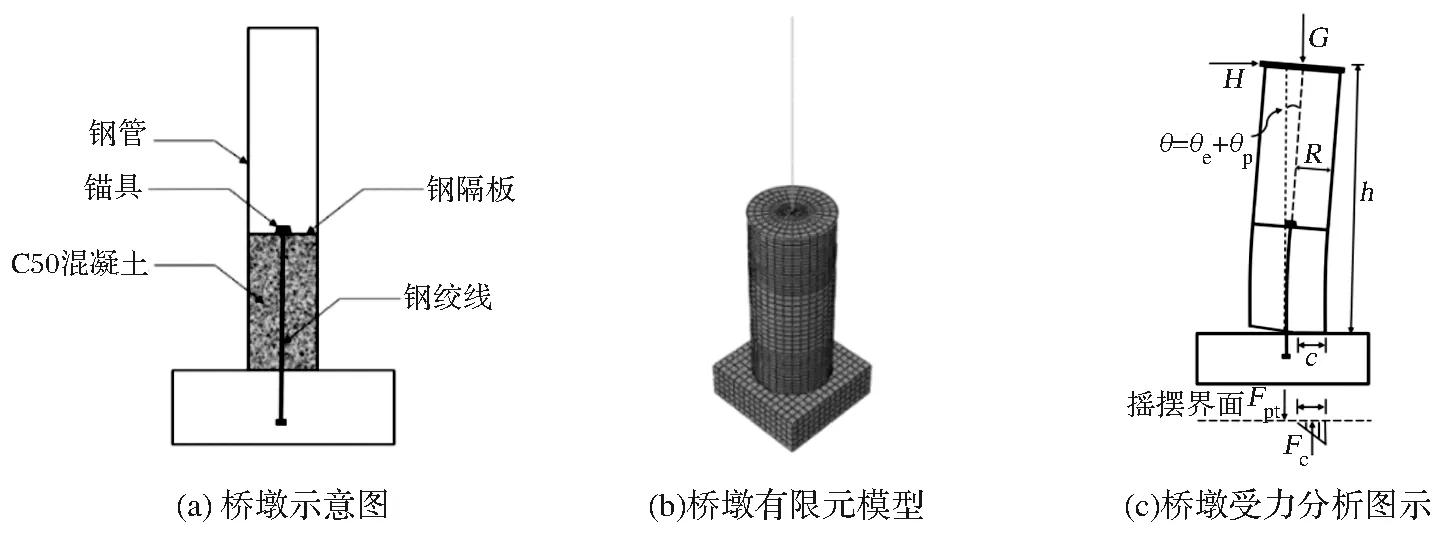
圖1 自復(fù)位部分填充鋼管混凝土橋墩結(jié)構(gòu)示意圖、有限元模型及受力分析圖示
鋼管和橫隔板采用Q345結(jié)構(gòu)鋼,預(yù)應(yīng)力鋼絞線采用1×7(七股)1860級高強(qiáng)鋼絲,內(nèi)填混凝土采用C50混凝土。鋼材本構(gòu)模型采用考慮包辛格效應(yīng)的隨動強(qiáng)化準(zhǔn)則,材料本構(gòu)選用二折線應(yīng)力-應(yīng)變本構(gòu)關(guān)系,混凝土本構(gòu)模型采用CDP模型。
在自復(fù)位橋墩墩頂施加恒定豎向荷載P,取值方式采用橋墩軸向屈服力的0.1倍,保持恒定的軸壓比不變。通過輸入幅值方式,在橫向施加水平往復(fù)荷載,加載位移以橋墩屈服位移為基準(zhǔn)進(jìn)行疊倍遞增[4],直至施加的位移達(dá)到墩高的1/25。
2.2 有限元分析結(jié)果
加載初期,在水平往復(fù)荷載作用下,橋墩的水平承載力迅速增加。當(dāng)橋墩和基礎(chǔ)產(chǎn)生開口間隙后,橋墩側(cè)向剛度降低,承載力增長變緩。水平荷載卸載至零時,橋墩在結(jié)構(gòu)自重和鋼絞線的共同作用下實(shí)現(xiàn)復(fù)位。當(dāng)水平荷載進(jìn)一步增加,由于橋墩根部鋼管出現(xiàn)局部變形,加載末期各模型的承載力均呈下降趨勢,如圖2。各模型的水平承載力-水平位移滯回曲線大致呈旗幟型,且卸載后的殘余位移較小,展現(xiàn)了結(jié)構(gòu)良好的耗能及復(fù)位能力。
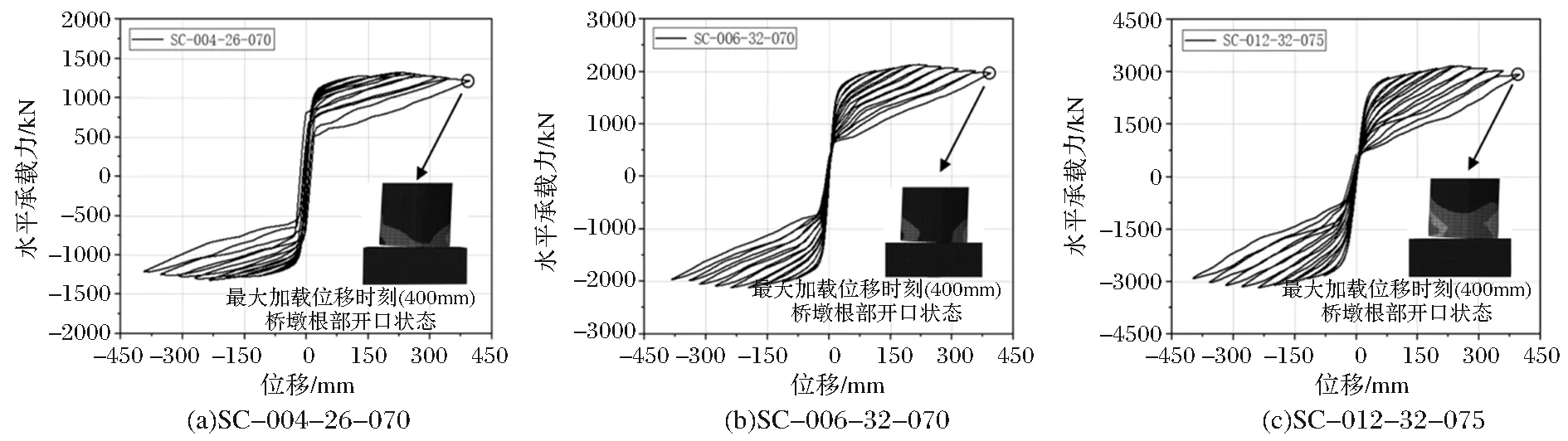
圖2 水平承載力-水平位移滯回曲線及開口狀態(tài)
由表1可知,壁厚為26mm的6個模型中,水平承載力最大為2563.1kN,最小為1286.0mm,對應(yīng)水平位移分別為279.5mm、202.1mm;壁厚為32mm的6個模型中,水平承載力最大為3294.9kN,最小為1657.2mm,對應(yīng)水平位移分別為279.0mm、159.4mm。隨著壁厚的增大,橋墩水平承載力提高,且滯回加載后的殘余位移降低;當(dāng)預(yù)應(yīng)力比由0.04增大至0.12,橋墩的水平承載力大大提高,墩底部位的應(yīng)力分布較為集中,如圖2(c),滯回后的橋墩損傷增大。在相同條件下,張拉度為0.7與0.75水平承載力-位移曲線大致重合,但加載后期張拉度為0.70的橋墩模型呈現(xiàn)出更優(yōu)的力學(xué)性能。
3 自復(fù)位部分填充鋼管混凝土橋墩力學(xué)性能理論分析
以自復(fù)位鋼橋墩力學(xué)性能理論推導(dǎo)為基礎(chǔ),考慮自復(fù)位部分填充鋼管混凝土橋墩與自復(fù)位鋼橋墩結(jié)構(gòu)上的差異。
(1)本橋墩,沿高度方向剛度有突變。
(2)本橋墩,預(yù)應(yīng)力鋼絞線施加的預(yù)應(yīng)力作用在鋼管和混凝土組合截面上。
為此針對這兩個方面進(jìn)行修正及理論分析。
3.1 沿橋墩高度剛度突變即高度參數(shù)Hp的考慮
以墩高方向為X軸,進(jìn)行橋墩位移分析。運(yùn)用懸臂梁原理進(jìn)行理論推導(dǎo),將結(jié)構(gòu)整體視為兩種不同剛度的組合體,具體簡化力學(xué)示意圖如圖3所示。
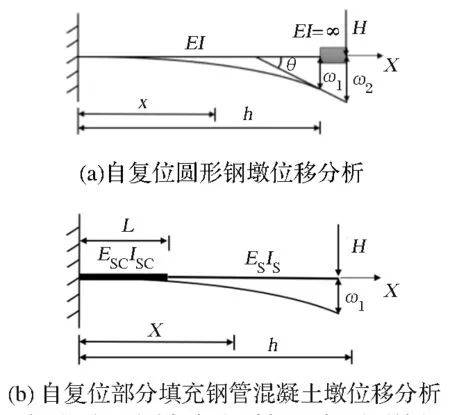
圖3 變剛度位移分析
(1)固定端處轉(zhuǎn)角θ0=0,撓度ω0=0,對于橋墩下部的鋼管混凝土部分(0≤x≤L):
(3)
其中:L為填充混凝土的高度,h為橋墩高度,H為水平荷載,Esc、Isc分別為鋼管混凝土的彈性模量與截面慣性矩,其計算方法依照《鋼管混凝土混合結(jié)構(gòu)技術(shù)規(guī)范》(GB 50936—2014)。根據(jù)簡化懸臂梁模型梁端的位移邊界條件,將微分方程一次、二次積分可分別計算得出填充混凝土頂部位置(x=L)處的轉(zhuǎn)角θL與位移ωL。
(2)當(dāng)處于空鋼管范圍內(nèi)時,轉(zhuǎn)角θ0=θL,撓度ω0=ωL,撓曲軸近似微分方程為:
(4)
其中:Es、As分別為外部鋼管的彈性模量與橫截面積。根據(jù)邊界位移條件,將上述微分方程二次積分可得墩頂位置處(x=h)的位移Δ,并進(jìn)一步由式(5)推導(dǎo)出高度參數(shù)Hp計算公式:
(5)
(6)
在墩底產(chǎn)生開口間隙前,自復(fù)位橋墩的力學(xué)響應(yīng)與普通基礎(chǔ)固結(jié)墩相似,則水平位移可通過式(6)進(jìn)行計算。墩底產(chǎn)生開口后,Φdec為開口曲率,自復(fù)位橋墩與普通基礎(chǔ)固結(jié)墩水平位移分別為:
(7)
其中:Φdec=G+F0/(EscAscR),由歐拉-伯努利梁理論得出。聯(lián)立上式,可得截面處最大法向應(yīng)變?yōu)椋?/p>
(8)
3.2 鋼絞線拉力Fpt與鋼-混凝土組合截面內(nèi)力平衡的考慮
在計算鋼絞線力時,假定重力荷載在鋼絞線預(yù)張拉后施加,同時考慮結(jié)構(gòu)總重力荷載和鋼絞線中力而導(dǎo)致的橋墩壓縮變形。鋼絞線中力和重力荷載共同導(dǎo)致的軸向應(yīng)變ε為:
(9)
其中:R為橋墩半徑;c為橋墩底部壓縮區(qū)長度;Lpt為鋼絞線長度;Ept、Apt為鋼絞線的彈性模量與橫截面積;G為橋墩重力。考慮軸向應(yīng)變導(dǎo)致的柱壓縮變形,可得到鋼絞線力Fpt更為精確的計算公式:
(10)
橋墩搖擺受力機(jī)制如圖1(c)所示,墩底壓力Fc可采用積分方法計算,式(12)檢驗截面受力平衡:
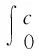
(11)
Fc=G+Fpt
(12)
理論計算時,先假設(shè)壓縮區(qū)長度初始值c,利用式(10)與式(11)計算鋼絞線力和墩底壓力,對c進(jìn)行迭代,直至滿足截面受力平衡。根據(jù)墩柱端截面彎矩平衡,橋墩水平承載力H按下式計算:
(13)
3.3 理論分析與數(shù)值分析對比
為了驗證自復(fù)位部分填充鋼管混凝土橋墩理論分析的準(zhǔn)確性,將模型SC-004-32-070、SC-006-32-070的數(shù)值分析水平承載力-水平位移骨架曲線與理論分析的數(shù)據(jù)進(jìn)行對比,如圖4所示。
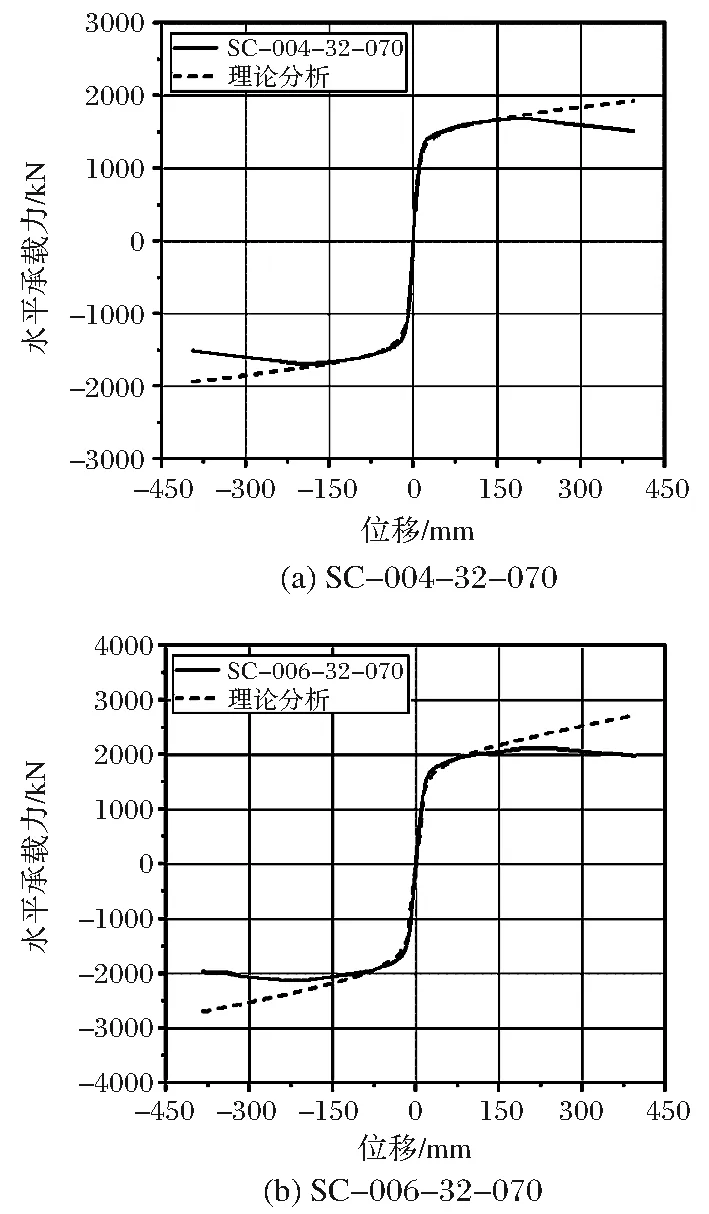
圖4 理論分析與數(shù)值分析擬合結(jié)果
由對比結(jié)果可知,理論分析在加載初期具有較好的預(yù)測精度,而中后期隨著荷載的增大,開口間隙出現(xiàn),由于各結(jié)構(gòu)組件存在摩擦、鋼管局部屈曲、鋼絞線斷裂等現(xiàn)象,理論分析的預(yù)測結(jié)果存在一定誤差。
4 結(jié)論
(1)橋墩鋼管壁厚和預(yù)應(yīng)力比主要影響橋墩的水平承載力,數(shù)值模擬結(jié)果顯示,鋼管壁厚在26~32mm范圍內(nèi),壁厚越大,橋墩的水平承載力越高,抗屈曲能力也隨之增強(qiáng)。預(yù)應(yīng)力比對結(jié)構(gòu)水平承載力起決定性的作用,在研究范圍0.04~0.12內(nèi),隨著預(yù)應(yīng)力比的增大,自復(fù)位橋墩的水平承載力增大,但另一方面,滯回后的橋墩損傷,即殘余位移也會隨之增大。
(2)預(yù)應(yīng)力鋼絞線張拉度對自復(fù)位橋墩的力學(xué)性能影響較小,但可以通過適當(dāng)?shù)亟档弯摻g線初始張拉應(yīng)力,提高鋼絞線冗余值,對于提高自復(fù)位橋墩的安全性具有積極意義。
(3)針對自復(fù)位部分填充鋼管混凝土橋墩所提出的理論計算方法,具有較好的預(yù)測精度,能夠指導(dǎo)工程實(shí)踐,具有一定的現(xiàn)實(shí)意義。

