基于C-Vine Copula熵多目標優化模型的水文氣象站網優化研究

徐鵬程，李 帆，張昌盛，仇建春

（1.揚州大學水利科學與工程學院，江蘇 揚州 225009；2.江蘇省水利建設工程有限公司，江蘇 揚州 225009）

0 引 言

準確完整的水文氣象數據對于水利工程項目設計、規劃和施工是至關重要的。水文氣象站網可以為水資源管理、水庫運行、洪水預報等提供必要和實時的基礎輸入信息。現代水文氣象站網應在滿足不同的用戶需求同時具備高效節約的特征。因此，水文氣象站網優化常常從多個目標函數的約束條件入手［1，2］綜合考慮站點的布設方式。

水文氣象站網的優化設計方法大致可以歸納為：①基于地統計學的方法［4，5］；②基于信息熵的評價方法［6-8］；③基于兩種及以上理論耦合的方法［9，10］。其中，信息熵方法在國內外水文站網優化中得到了廣泛應用，其基本原則是通過最大化站網信息總量，同時最小化信息冗余度從而獲得最優站點布置方案。Mishra 和Coulibaly［11］提出了用基于信息傳遞指數（Transfer Index，TI）的多元回歸模型有效量化了徑流站網的顯著性。Markus等［12］將信息傳遞指標法（Direct Transmission Index，DIT）和廣義最小二乘法（Generalized Least Square，GLS） 耦合并將站網信息量作為關鍵的懲罰函數對徑流站網進行了優化評估。Fuentes 等［13］提出了基于信息熵-效用（Entropy-Utility）標準對環境和空氣污染型樣本分析，并在非平穩性的假設下建立了基于信息熵框架下的貝葉斯最優子網絡和空間相關模型。Li等［14］采用了最大化信息量最小化冗余信息量的準則對水文徑流站網進行優化設計并考慮站網優化結果對序列離散化法的敏感性分析。

近年來，由于氣候變化和人類活動雙重影響，未來氣候變化情景下的水文氣象情勢存在很大的不確定性，另一方面降雨、洪水極端事件呈現出顯著的趨勢性和突變性［15-17］，為此進行站網優化時有必要關注未來氣候變化條件下水文氣象序列的趨勢特性［18］。同時由于離散化方法對于站網優化結果的影響較大［13，14］，為此Xu 等［19］采用阿基米德Copula 熵進行多維互信息的估計，盡管克服了互信息估計的不確定性，但是由于Archimedean Copula 函數［20-22］對于高維聯合分布的擬合誤差使得其對于高維冗余信息量的估計精度不夠。為此本文擬從兩個方面進行研究：①采用C-Vine Copula 函數擬合高維的聯合分布［］進而求得Copula 熵以提高對總相關量的估計精度；②從不同流域由于站網內部水文氣象序列的趨勢性出發，加強不同趨勢程度引發的序列非平穩特性對站網優化結果的敏感性分析。

1 基于C-Vine Copula 熵的站網優化基礎理論

1.1 C-Vine Copula函數

假定[X1，X2，…，Xd]是一個d個站點組成的站網，其聯合概率密度函數為p(x1，x2，…，xd)，變量X1，X2，…，和Xd對應的邊緣密度函數分別為pX1(x1)，pX2(x2)，…，pXd(xd)。多維聯合概率密度函數可以用如下公式求得：

式中：P（·）函數是多維累計聯合分布函數（Joint Cumulative Distribution Function，JCDF）；PXi是單變量Xi的邊緣分布函數；θ是Copula參數值。

由于阿基米德Copula 在高維聯合分布模擬的不足，本文通過將多元概率密度分解為一系列二元Copula，基于C-Vine Copula 函數解決上述問題［7］。按照變量間的相關性排序是確定Cvine Copula函數樹形結構的關鍵步驟。n維C-Vine Copula 的概率密度函數可以表達如下：

式中：fk(xk；θk) (k=1，2，…，n)表達了第k個變量的邊緣概率密度函數；ci，i+j|1：(i-1)為二維Copula密度函數。

為了說明C-Vine Copula函數的建立過程，同時由于篇幅的限制，本文以四維C-vine Copula 為例，圖1顯示了一個由4個變量和三棵樹組成的C-Vine結構。為了便于說明，數字1、2、3和4分別表示隨機變量x1，x2，x3和x4。這個圖示說明了建立C-vine copula 的過程。在第一棵樹中，變量x1起著關鍵作用（基于Kendall秩的分析［23，24］），處于樹一的結點，其余變量處于樹一的邊。同理樹二中變量x2起著關鍵作用，處于樹二的結點，以此類推。

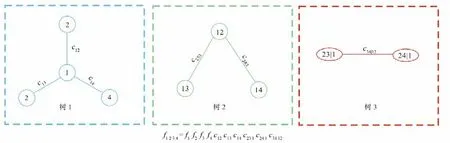
圖1 四維C-Vine Copula函數的樹形結構Fig.1 The tree strcture of four-dimensional C-vine Copula

1.2 C-Vine Copula熵為核心的站網優化模型

在獲得d個站點情形下的C-Vine Copula 函數，可以通過Copula 熵與總相關量（TC）之間互為相反數的數學關系，獲得所需站網優化過程中的兩個關鍵站網信息目標函數。

其中Copula熵可以表示為：

其中，c(u1，u2，…，ud) 是Copula 密度函數，主要可以采用兩種方法計算式（3）中描述的Copula 熵：①多重積分法；和②蒙特卡洛模擬法。由于多重積分法在維數較高時求解困難，本文采用了后一種方法計算Copula 熵。為此最終本文求得如下以Copula 熵為核心的兩個目標函數（最大化聯合信息量-最小化總相關量）：

其中，邊緣熵（H(Xi)）本文擬通過極大熵原理（POME）進行求解，而Copula 熵則是從C-Vine Copula 函數角度出發，首先估計C-Vine Copula參數，進而采用蒙特卡洛模擬獲得隨機數的思路估計C-Vine Copula 熵；接著按照公式（4）獲得兩個目標函數值；最終通過多目標優化求得帕累托最優解集的方法獲得最優站點組合。傳統的多維阿基米德Copula 函數只具備一個自由度的參數無法涵蓋高維情形下的所有可能的尾部依賴性，維數較高的阿基米德族Copula 函數更適合于擬合具有正相關的多變量相依性結構，為此本文擬從C-Vine Copula角度進行多站點間的相依性結構的擬合從而獲得準確的Copula熵值。

2 研究區域

作為中國最為典型的兩個代表性流域，在過去幾十年以來，其流域的水文氣象情勢和氣候變化、人類活動存在顯著的響應關系。本文為了對比不同趨勢程度對站網優化結果的影響，分別選取了黃河流域和淮河流域43個雨量站組成的初始站網（圖2）并都選用了1992-2018年的日降水量觀測序列作為研究對象，考慮到Copula 函數的獨立同分布假設并對降雨數據進行了前處理以消除零降雨值對序列自相關的影響。首先分析了全序列的優化結果；為了加強優化結果對趨勢性的敏感性分析，分別采用25年，20年，10年，5年和2年的滑動窗口法進行子序列的二次優化分析。

圖2 黃河和淮河流域雨量站分布Fig.2 Distribution of rainfall stations in the Yellow River and Huaihe River Basin

3 站網優化結果

3.1 基于全序列的站網優化結果

由于帕累托解集的不唯一性且考慮到站點組合數的眾多，為了提高優化效率，本文通過隨機生成10 000 個站點組合，從中選取滿足式（4）中兩個目標函數的帕累托解集，并采用統計學的方法統計帕累托解中的各站點出現累計頻率，最終站點優化結果見圖3。其中紅色圓圈的直徑大小代表了帕累托解中站點出現頻率的多少。由圖3可知，對于淮河流域而言，高頻率站點主要出現海拔較高的山丘區域低頻率站點主要存在于平原地區；而對于黃河流域而言，高頻率和低頻率的站點分布混合分布在流域內并沒有呈現顯著的海拔分布效應。

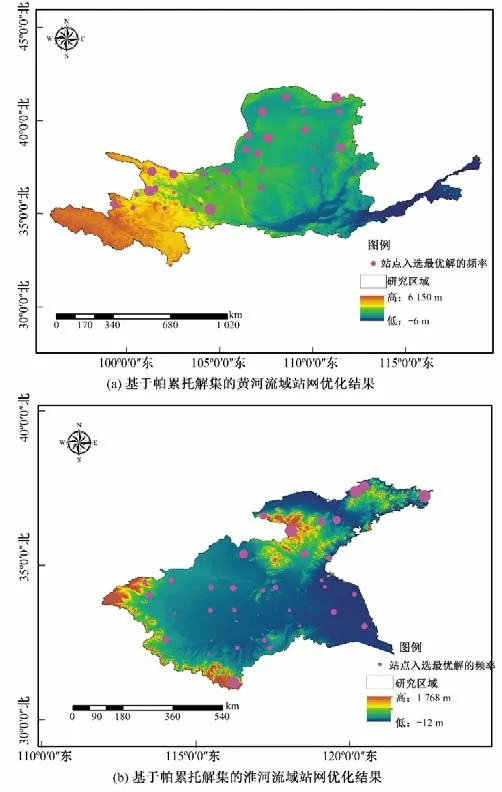
圖3 黃河和淮河流域全序列優化結果Fig.3 The optimization results based on whole sequence of Yellow River and Huaihe River Basins

3.2 總相關量估計精度分析

為了對比分析阿基米德Copula 函數和C-Vine Copula 函數估計總相關量時的差異性，本節分別計算了k站點組成（k=1，2，3，…，43）最優站點組合中的總相關量；并將離散化方法（直方圖法）計算得到總相關量作為參照樣本。具體結果見圖4，其中維度為10 代表10站點組成的最優站點組合所包含的冗余信息量（即總相關量）。由圖4可知，由于C-Vine Copula 函數在高維聯合擬合的優勢，其按照蒙特卡洛隨機模擬求得總相關量和直方圖法求得總相關量之間是比較接近的，而阿基米德Copula 函數由于在高維聯合分布擬合的不足，其總相關的估計值隨著維數越來越高越發的偏離直方圖法計算得到冗余信息量。這在一定程度上表明了采用C-Vine Copula 函數去估計總相關量這一思路是可行的且具有比阿基米德Copula 函數精度更優的優勢。

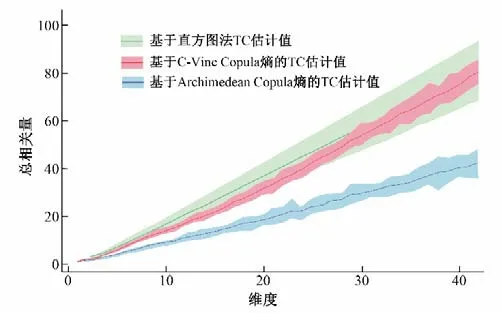
圖4 總相關量估計對比Fig.4 Comparison of total correlation estimation

3.3 站點優化結果對序列趨勢性的敏感性分析

由于兩個流域研究降雨序列的趨勢程度的不同（圖5），可以發現淮河流域43 個站點中有41 個站點都通過了5%顯著水平的Mann-Kendall（MK）檢驗，而黃河流域只有6個站點呈現顯著的上升趨勢性。為此有必要研究趨勢性程度的不同對站網優化結果的影響。

圖5 黃河與淮河流域序列趨勢分析結果（MK檢驗）Fig.5 Trend analysis results of the Yellow River and Huaihe River Basin Series （MK test）

為了量化站網優化結果對趨勢性的敏感性分析，本節基于不同窗寬（Sliding Windows，SW）條件下的降雨子序列進行站網的二次優化。由圖3中結果可知，站點入選帕累托解集呈現頻率差異性，后續的敏感性分析按照入選頻率對各站點進行了降序排序（秩次越小代表其越重要）。由圖6可以發現淮河流域在不同窗寬條件下的優化結果存在顯著的差異性，只有在站點S8，S31 和S43 有一定的相似性（圖6中黃河流域3 個站點所在行處于藍色系，其余站點所在行在藍色、黃色和紅色色系間不斷波動）。而黃河流域不同窗寬條件下站點的排序結果相似性較為顯著。

圖6 不同窗寬條件下黃河和淮河流域站點秩次圖Fig.6 Rank map of Yellow River and Huaihe River Basin station under different window width conditions

為了能夠直觀顯示站點排序結果的差異性，又對各窗寬條件下的子序列（秩次序列）進行了相關性分析；如窗寬等于5年時，有23 個子序列，兩兩之間配對可以產生C223=253 個相關系數，并對這些子序列相關系數的經驗分布形態進行了計算分析（見圖7）。圖7中橫向比較可以發現，各窗寬下淮河流域排序子序列的相關程度明顯弱于黃河流域的排序子序列。縱向比較可以發現，隨著窗寬的不斷減小，排序子序列的相關程度在不斷減弱。

圖7 不同窗寬條件下排序子序列的相關性分析Fig.7 Correlation analysis of rank subsequences with different window widths

總體來看，由于淮河流域的顯著趨勢性使得其站網的優化結果對于窗寬的敏感性較強而趨勢性程度較弱的黃河流域其站網優化結果對于窗寬的敏感性較弱；趨勢程度較大的淮河流域站網秩次的年際變化相比于趨勢程度小的黃河流域站網更加顯著。

4 分析與討論

基于信息熵的站網優化方法常常是水文氣象站網優化領域常用的方法，但是受限于離散化手段的高度敏感性，使得其計算過程有很大的不確定性［6，7］。前人研究表明動態化箱寬和固定箱寬的離散化方法進行了比較，發現對最佳站網方案的影響不容忽視［9］。受到其計算能力的限制，早期大多數研究使用擬合分布或核密度估計來估計信息熵值，但其計算精度，特別對于多變量的冗余信息量估計值效果不佳［9，10］。圖4中的直方圖法較寬的TC 估計置信區間很好地應證了這一點。本研究采用C-Vine Copula 函數較為精確地模擬多站點間高維相依性結構，一方面可以克服信息熵離散化方法引發的優化結果的不確定性問題，另一方面相比于傳統阿基米德Copula 函數提高了高維依賴性結構的模擬精度，從而實現對站網優化的兩個目標函數：信息總量和總相關量的精準估計。

此外，時間變異性和空間差異對水文氣象站網優化設計的影響得到了廣泛關注［14，16］。在水文氣象站網優化設計過程中，氣候變化、人類活動和水文過程的非平穩性不容忽視，尤其是對于高度異質性、局部性且受地理、地形和氣候因素強烈影響的降雨事件。不同的時間域范圍可能會對站網設計結果產生不同的影響，這意味著最佳的站網布設可能只適用于特定的觀測時段。盡管前人對于站網優化開展了大量工作，但是從水文氣象時間序列的非平穩性入手應對氣候變化背景下水文氣象站網優化的動態分析工作是有限的。本研究著重討論了中國兩個典型的流域（淮河流域和黃河流域）由于各自對于氣候變化響應程度的不同（黃河流域趨勢型非平穩性較弱，淮河流域較強）其最終站點優化秩次呈現不同的變化形態。因此，本研究表明在處理水文氣象站網優化時應非常謹慎，因為在其他條件相同情形下，基于固定的全序列剔除或者增加某些臺站會導致整個站網系統的水文氣象信息損失或信息冗余。根據本文的研究結果，站網的優化設計應當以使其更適應不斷變化的水文氣象條件可能更為可取。

5 結 論

（1）Archimedean Copula 函數由于僅僅適用于正相關的多變量相依性結構，特別是對于高維聯合分布的擬合精度無法準確刻畫潛在的高維相依性結構的尾部特征，最終使得其對于高維冗余信息量的估計精度明顯不夠。為此本研究擬從C-Vine Copula 函數出發開發基于C-Vine Copula 熵的多目標站網優化模型，一方面有效提高了阿基米德Copula熵總相關量的估計精度，另一方面有效實現了對于水文氣象站網過程中最大化站網信息總量和最小化信息冗余量的兩個目標函數的求解，基于兩個典型研究區域的計算結果可知，本文提出的C-Vine Copula熵具有較好的適用性和可行性。

（2）在水文氣象站網優化設計過程中，氣候變化、人類活動和水文過程的非平穩性不容忽視。一方面趨勢性引發的序列非平穩特征增加了未來氣候變化背景下水文氣象站網優化的不確定性，另一方面不同的時間域范圍可能會對站網設計結果產生不同的影響。基于淮河和黃河流域的計算結果可知：趨勢性較強的淮河流域隨著窗口期的不同，子序列的秩次年際變化明顯強于趨勢性較小的黃河流域。為此，在氣候變化的背景下進行水文氣象站網優化分析時，有必要考慮站點序列的趨勢性從而引發的非平穩特性對站網優化結果的影響。