水輪機調節系統的動態滑模控制

付文龍，張仕海，鄭 陽，盧啟鵬，徐 潘

（1.三峽大學電氣與新能源學院，湖北 宜昌 443002；2.武漢大學動力與機械學院，湖北 武漢 430072；3.三峽大學 梯級水電站運行與控制湖北省重點實驗室，湖北 宜昌 443002）

0 引 言

近年來，電力系統的能源結構發生了巨大的變化［1］。這主要是由于一些可再生能源的快速發展，如風電、光伏發電、水電等，在能源供應中的比例日益增加［2］。由于風能和光能的間歇性和波動性使得電網的安全穩定運行受到了更多的挑戰。水力發電機組作為電網中起調節作用的重要組成部分，為了使電網能夠安全穩定運行，所以有必要研究水力發電機組的控制策略［3］。水輪機調節系統是水力發電機組的控制系統，根據功率輸出設定值和轉速設定值控制水輪機的轉子轉速以達到對電網輸出功率的控制［4］。因此建立合適的水力發電機組模型和設計合適的控制策略至今仍是一個值得研究的問題。

在過去的幾十年里，相關學者對水輪機調節系統的建模和控制方法進行了大量的研究。例如，郭文成等［5］建立了帶調壓井的水電站調速系統的數學模型，并對其穩定性進行了分析。楊建東等［6］對兩種調節方式下的水電站調速系統建立了4個模型，并分析了簡化模型對穩定性的影響。楊威嘉等［7］通過對抽水蓄能機組的建模、協同優化和運行評估的研究，提高了抽水蓄能機組的調節性能。

隨著水輪機調節系統建模的發展，控制器的設計也得到了重大的改進。水電站的功率輸出主要是通過改變水輪機的轉速從而控制扭矩以達到對輸出功率的控制。目前主要通過PID控制器對水電機組的輸出功率進行控制。然而，水輪機具有非線性特性和不斷變化的負荷使得傳統的PID 控制面臨巨大挑戰。因此，為了提高水電機組的控制品質，近年來許多學者基于經典控制理論和現代控制理論開發了許多先進的控制方法，如模糊控制、預測控制和前饋控制［8］。許顏賀等［9］為了克服水泵水輪機’S’特性區域引起的空載啟動條件下的轉速振蕩，運用模型預測和模糊控制理論，研究了抽水蓄能機組在低水頭下空載啟動的最優控制。王斌等［10］研究了一種用于時滯水輪機調節系統的模糊廣義預測控制方法。陳帝伊等［11］研究了非線性水輪機調節系統的自適應輸出反饋容錯控制問題。雖然以上控制方法能夠對非線性水輪機調節系統進行控制，但是不能保證系統具有魯棒性。

滑模控制作為重要的魯棒控制策略和非線性控制方法，在水電機組的運行控制領域受到廣泛應用［12］。但是滑模控制的不連續性使得滑模控制在到達滑模面后，會在滑模面兩側出現高頻、小幅度的抖振，而且水輪機調節系統中存在的時滯開關和系統慣性也會引起高頻抖振，所以將滑模控制應用于水輪機調節系統的控制中也會存在抖振問題且一直沒有得到解決。為了解決上述問題并提高水輪機調節系統的控制品質，本文以水輪機調節系統的非線性模型為基礎，根據滑模控制理論，提出了動態滑模控制策略，設計了基于動態切換函數的動態滑模控制器；然后采用智能優化算法結合時間乘誤差平方積分準則（ITSE）對設計的控制器參數進行了尋優；最后通過對比實驗對設計的動態滑模控制器的有效性和控制性能進行了驗證。仿真結果表明設計的動態滑模控制器顯著的降低了系統中的抖振問題，并且能夠有效的控制水電機組運行在穩定狀態。

1 水輪機調節系統的非線性模型

具有超長引水隧洞的水輪機調節系統的結構框圖見圖1所示。由圖1可以看出水輪機調節系統主要由控制系統和被控系統組成。整個系統可以通過壓力管道、電液伺服系統、水輪機和發電機組的數學模型來構建［13］。建立了超長引水隧洞的水輪機調節系統［14］。

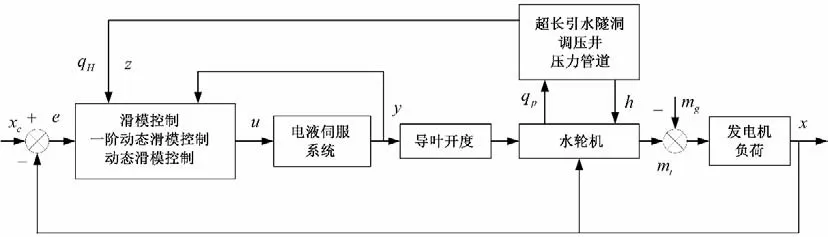
圖1 水輪機調節系統結構圖Fig.1 Structure diagram of hydraulic turbine governing system

超長引水隧洞的非線性動力學方程為［15］：

式中：TwH0為超長引水隧洞的水流慣性時間常數；z為調壓室水位變化；hH0為超長引水隧洞的水頭損失；H0為水輪機水頭；qH為超長引水隧洞的流量。

調壓室的動力學方程［16］：

式中：qP為壓力管道的流量；TF為調壓室的時間常數。

對于水輪機調節系統的動態性能和控制問題，假設水電站運行在額定工況，外部擾動為小擾動。具體而言，水輪機轉速、水頭和導葉開度的變化較小，而且水輪機的非線性特性較弱［17-19］，所以將水輪機模型進行線性化建模。水輪機的力矩和流量方程［15］如式（3）：

式中：eh，ex，ey表示水輪機的力矩傳遞系數；eqh，eqx，eqy表示水輪機的流量傳遞系數；mt為水輪機動力矩偏差相對值；x為水輪發電機組轉速偏差相對值；y為導葉開度偏差相對值。

同步發電機的一階方程如式（4）所示［20，21］：

式中：Ta為發電機組的慣性時間常數；mg為電網的負載擾動；eg為水輪發電機組的自我調整系數。

電液伺服機構作為水輪機的執行機構，用于放大控制信號，并提供足夠的功率來控制導葉機構動作［22］。電液伺服系統的動力學方程如式（5）所示：

式中：Ty為伺服系統的時間常數；u是控制器輸出。

基于上述數學模型可以建立水輪機調節系統的狀態空間方程組為：

對于n階非線性動力系統，為了便于控制器設計，水輪機調節系統的狀態空間方程組可以轉換為如下標準形式。

式中：X為系統的狀態向量；A（X）、B是n維向量場；u是有限控制輸出；Y是輸出向量。X、A（X）、B和h（X）分別如下式所示：

式（7）的主要目的是找到理想軌跡xd的控制律，使得水輪機調節系統的輸出跟蹤理想軌跡，從而使跟蹤誤差xd-x趨于零。

2 水輪機調節系統的動態滑模控制策略

2.1 基于動態切換函數的水輪機調節系統動態滑模控制

動態滑模控制方法的主要思想是在滑模控制器和受控對象之間插入積分器。水輪機調節系統的動態滑模控制框圖如圖2所示。由于經過了積分器對高頻抖振的過濾作用，實際受控對象的控制輸入u就變得連續，從而減少了系統的抖振問題。這種動態滑模控制策略能夠消除抖振并確保零穩態誤差。

圖2 水輪機調節系統的動態滑模控制框圖Fig.2 Block diagram of dynamic sliding mode control for hydraulic turbine governing system

選擇系統狀態變量的跟蹤誤差為：

基于動態切換函數的動態滑模控制的切換函數為：

其中：

為了迫使系統盡快到達滑模面，選擇指數趨近律如式（15）所示。

將式（13）兩邊同時對時間求導數為：

式中：

由于式（16）中不含有滑模控制律u，所以將式（6）中的第三項對時間求二階導數可以得到狀態變量x的三階導數為：

將式（17）～（19）代入式（16），求得動態滑模控制器的控制律u如式（20）：

式中：

采用李雅普諾夫穩定性進行系統穩定性檢驗，選擇李雅普諾夫函數為V=s2∕2［27，28］。李雅普諾夫函數的導數為：由式（31）可知新的切換函數σ是漸進穩定的。當t→∞時，σ→0，系統能夠在有效時間內到達滑模面σ=0。

2.2 水輪機調節系統的一階動態滑模控制

針對一階動態滑模控制，設計的切換函數與控制輸入的一階導數有關，新的切換函數為：

式中，c1＜0，c2＜0；c3＞0。

同理，采用指數趨近律設計一階動態滑模控制器，求得一階動態滑模控制律u為：

式中：

由李雅普諾夫穩定性可知，設計的一階動態滑模控制器能夠使系統保持穩定運行。

3 滑模控制器的參數優化

對于控制器的設計，參數的設置也是控制器設計中的一個重要因素，因此，有必要對控制器的參數進行優化。參數優化需要對系統建立目標函數和選擇適當的方法。傳統上，工程師手動調整參數的調節時間過長且很難達到最優，所以有必要選擇更為有效的方法。目前對參數優化的研究主要有智能優化算法和進化算法。進化算法由于其基于種群的搜索方法和并行特性，進化算法在工程中得到了廣泛的應用［29，30］。

本研究采用PSOGWO 混合優化算法對水輪機調節系統進行滑模控制器參數優化的流程圖如圖3所示。

圖3 基于PSOGWO算法的水輪機調節系統滑模控制參數優化流程圖Fig.3 Flow diagram for optimization of slide mode control parameters of hydraulic turbine governing system by PSOGWO algorithm

設計的3 種滑模控制器都需要對參數尋優，因此對每個控制器使用相同的目標函數對控制器參數進行尋優。根據ITSE性能指標設計的系統控制器可以抑制過度過程中較大的偏差和過度過程時間。因此將ITSE 作為3 種控制器參數尋優的目標函數，并通過PSOGWO 優化算法尋優，然后通過尋優的參數進行仿真實驗，以驗證3種滑模控制策略對系統控制的有效性。

性能指標函數如式（38）所示：

4 仿真驗證

在本節中，利用Matlab 軟件對水輪機調節系統進行了仿真，并將設計的動態滑模控制器應用于控制系統的軌跡追蹤。通過與常規滑模控制器的比較可以驗證設計的控制器的有效性。系統（7）的參數如表1所示。

表1 水輪機調節系統的參數Tab.1 Parameters of the hydraulic turbine governing system

為了驗證所設計的控制器的有效性和不喪失通用性的情況下，選擇正弦信號和階躍信號作為系統（7）中的輸入信號。采用上節分析的ITSE 指標作為目標函數，并用PSOGWO 優化算法對三種滑模控制器進行參數尋優。3種控制策略分別在正弦信號和階躍信號下的優化參數如表2、3和表4所示。

表2 動態滑模控制器的最優控制參數Tab.2 Optimal control parameters of dynamic sliding mode controller

表3 一階動態滑模控制器的最優控制參數Tab.3 Optimal control parameters of first-order dynamic sliding mode controller

表4 滑模控制器的最優控制參數Tab.4 Optimal control parameters of sliding mode controller

3種控制器在正弦信號和階躍信號下對系統輸出的軌跡追蹤曲線見圖4至圖6。從圖4至圖6可以看出3種滑模控制器對階躍信號和正弦信號都可以很快追蹤，沒有出現明顯的超調和振蕩。設計的一階動態滑模控制器和動態滑模控制器在水輪機調節系統的定點穩定中具有較短的過渡時間和相對穩定的暫態過程。由圖4至圖6的正弦信號的軌跡追蹤曲線可以得出，利用設計的動態滑模控制器可以使系統穩定在選擇的周期軌道上；而且設計的動態滑模控制器對水輪機調節系統在周期軌道跟蹤下具有良好的動態響應。顯然，水輪機調節系統的給定信號無論是階躍信號還是正弦周期信號，所提出的動態滑模控制器都具有較好的跟蹤能力和魯棒性。

圖4 不同給定信號下滑模控制的軌跡追蹤曲線Fig.4 Trajectory tracking curves for sliding mode control with different given signals

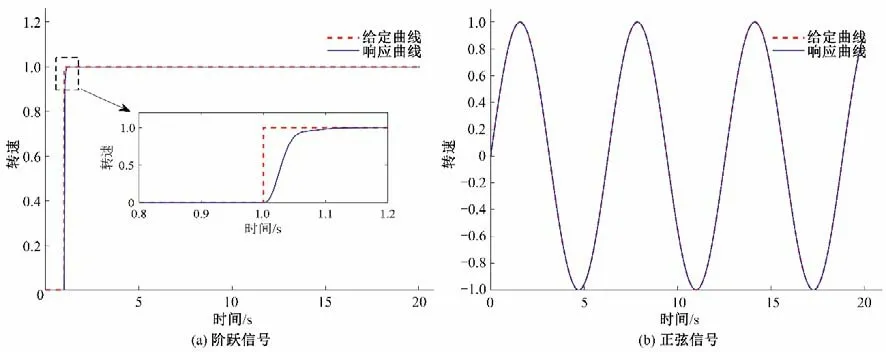
圖5 不同給定信號下一階動態滑模控制的軌跡追蹤曲線Fig.5 Trajectory tracking curves for first-order dynamic sliding mode control with different given signals

圖6 不同給定信號下動態滑模控制的軌跡追蹤曲線Fig.6 Trajectory tracking curves for dynamic sliding mode control with different given signals

為了便于分析和比較3 種控制策略對系統的控制性能，進行了3 種控制器的對比實驗。利用提出的動態滑模控制器，水輪機調節系統可以穩定到任意的固定點。假設固定點選擇為xd=1（t），采用3種控制器來調整水輪機調節系統的響應。

從圖7（a）可以看出，3種控制器都能在較短時間穩定，但是常規滑模控制器和一階動態滑模控制器在固定點周圍發生抖動，且抖動較為顯著。由圖8（a）可以看出，轉速誤差信號在穩定后，常規滑模控制和一階動態滑模控制有很強的抖動并且誤差變化較為顯著。從圖7（b）可以看出3 種控制器對正弦信號的軌跡追蹤效果都很好，但是從圖8（b）可以得出動態滑模控制器對水輪機調節系統的控制性能較好。因此，設計的動態滑模控制器能夠對水輪機調節系統進行有效的控制，而且系統具有更好的動態響應。圖9顯示了3 種控制器在不同參考信號下的控制器輸出曲線。由圖9可以看到，常規滑模控制器和一階動態滑模控制器出現了較為嚴重的抖振，但是動態滑模控制器的輸出很平滑，沒有出現抖振現象。上述分析表明動態滑模控制器不僅解決了常規滑模控制器設計時出現的抖振現象，而且對水輪機調節系統的控制效果十分優秀。

圖7 3種控制器在不同參考信號下的軌跡追蹤曲線Fig.7 Trajectory tracking curves of three controllers under different reference signals

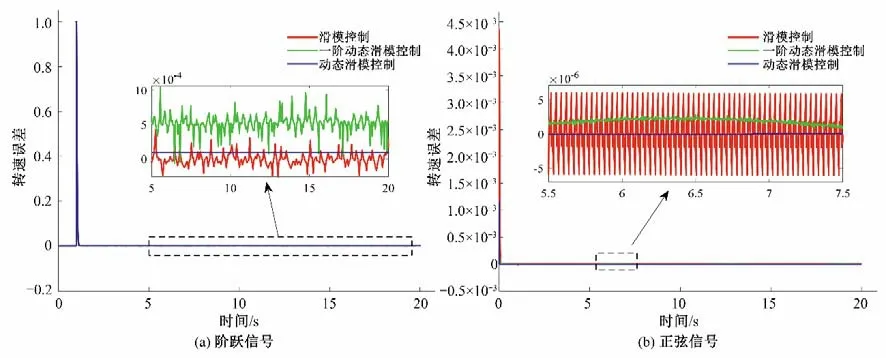
圖8 3種控制器在不同參考信號下的轉速誤差曲線Fig.8 Speed error curves of three controllers under different reference signals

圖9 3種控制器在不同參考信號下的控制器輸出曲線Fig.9 Controller output curves of three controllers under different reference signals

5 結 論

本文設計了動態滑模控制器，用于水輪機調節系統的精確跟蹤控制。在水輪機調節系統建模中，首先采用四階微分方程來描述水輪機調節系統的非線性特性，然后使用動態滑模控制策略來建立控制律u和水輪機轉速x之間的關系。基于仿真模型，將所提出的動態滑模控制器在不同參考信號下進行了比較。實驗結果表明，所提出的動態滑模控制器不僅可以在不同給定信號下以較短的時間跟蹤參考信號，而且提高了非線性水輪機調節系統的控制性能。此外，仿真結果也驗證了動態滑模控制器相對于傳統滑模控制器的優越性，并證實了動態滑模控制器可以有效降低滑模控制面臨的抖振效應。