不同插值方法對典型固體潮水位插值結果比較

韓孔艷 崔博聞 孫小入 費伯秀

1 北京市地震局，北京市蘇州街28號，100080

地震前兆觀測數據多是等間隔采樣的，觀測過程中如果受停電、儀器故障等影響會導致數據缺失。但對前兆數據進行統計分析時，往往要求數據序列必須是一個連續完整的數據集，不能包含缺失值。地下流體水位觀測是地震前兆臺網重要觀測手段之一,在前兆異常提取、地震預測研究、震情跟蹤中發揮著重要作用。由于觀測井條件和受干擾因素等不同，各種頻率信息疊加使水位數據形態各異[1-2]。因此，研究不同缺值情況下典型水位的最佳插值法極為必要。

1 插值方法及水位數據

1.1 插值方法及評價標準

本文選用5種常用的數據插值方法：最鄰近插值法、線性插值法、三次多項式插值法、三次樣條插值法和ARMA模型預測插值法。其中，ARMA模型預測插值法使用缺失值前360個數據的一階差分作為建立ARMA模型的基礎，通過確定模型階數、估計模型參數和殘差分析判定最佳的ARMA模型，利用模型預測數據作為插值結果[3-4]。本文利用插值與觀測值的均方根誤差RMSE的大小、變化情況來評估5種插值法對3種典型固體潮水位數據的插值效果。

1.2 水位數據篩選

水位變化分為宏觀動態和微觀動態，對淺部承壓含水層來說，宏觀動態變化較明顯；隨著含水層埋深越來越深，微觀動態增強[1-2]。本文根據水位變化特征，篩選出具有固體潮效應的9口觀測井的3類典型水位數據，觀測井信息見表1，3類典型水位數據變化特征如下。

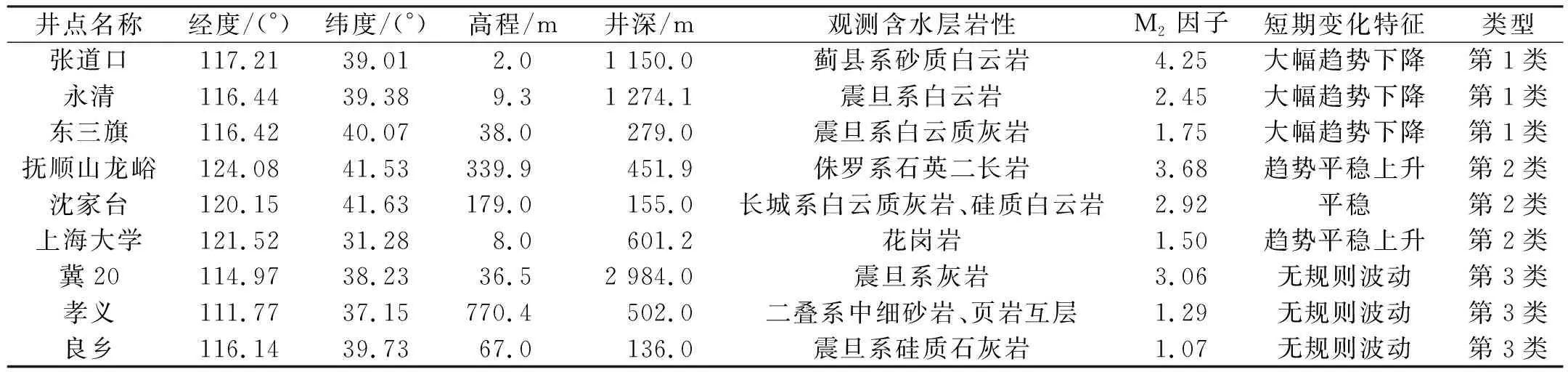
表1 9口固體潮觀測井的詳細信息Tab.1 The detailed information of nine solid tide observation wells

第1類數據趨勢變化較大，固體潮被壓制。該類觀測井普遍受地下水開采和降雨徑流補給影響，如張道口井、永清井和東三旗井。3口井水位最大月變幅分別為5.25 m、8.06 m和2.71 m，最大日變幅分別為0.44 m、0.40 m和0.25 m，表現為快速大幅上升或下降，有清晰固體潮，但被壓制在趨勢變化之下。

第2類數據趨勢變化平穩，固體潮明顯。該類觀測井受開采和降雨影響小，如撫順山龍峪井、沈家臺井、上海大學井。3口井水位最大月變幅分別為0.56 m、0.25 m和0.29 m, 最大日變幅分別為0.26 m、0.23 m和0.11 m，固體潮波動與趨勢、日變幅差距不大，潮汐波動明顯。

第3類數據起伏波動，固體潮清晰。該類觀測井易受淺層開采和降雨直接補給影響，如冀20井、孝義井和良鄉井。3口井水位月變幅分別為0.45 m、0.47 m和0.93 m，日變幅分別為0.19 m、0.22 m和0.22 m，既有固體潮波動，月變和日變也存在較大起伏。

2 不同插值結果對比分析

2.1 插值方案

選取上述9口觀測井2016年相近時段水位整點值序列180組，每個類型60組，每組不小于480個數。人為設計缺失1/4 d、1 d、2 d和3 d的情況，用前述5種插值法對缺失序列進行插值，分別計算每種插值的RMSE。另選3類、12組數據進行回溯性檢驗。

2.2 不同插值結果的對比分析

從3類數據的RMSE變化曲線(圖1)和優勢插值法占比情況(表2)可知，在連續缺失1/4 d的情況下，三次多項式插值法的RMSE值小且波動小，3類數據的優勢占比分別為96.67%、63.33%和88.33%，表明該方法對少量數據缺失的插值優勢比較突出。線性插值法對第1類數據缺1 d、2 d和3 d的情況插值優勢較大，最優占比最大達71.67%(表2)，且對第3類數據的插值優勢與ARMA模型預測插值法基本相當，兩者最優占比之和為91.66%，是缺失較多的第3類數據較優的2種插值方法。ARMA模型預測插值法的RMSE波動最小(圖1)，特別是對第2類數據，其插值最優比都在80%以上(表2)，是不同缺值情況下該類數據的最優插值方法。隨著缺失值的增加，各插值法的誤差有增大的趨勢，但ARMA模型預測插值法的變化幅度相對較小，其優勢一直很明顯。

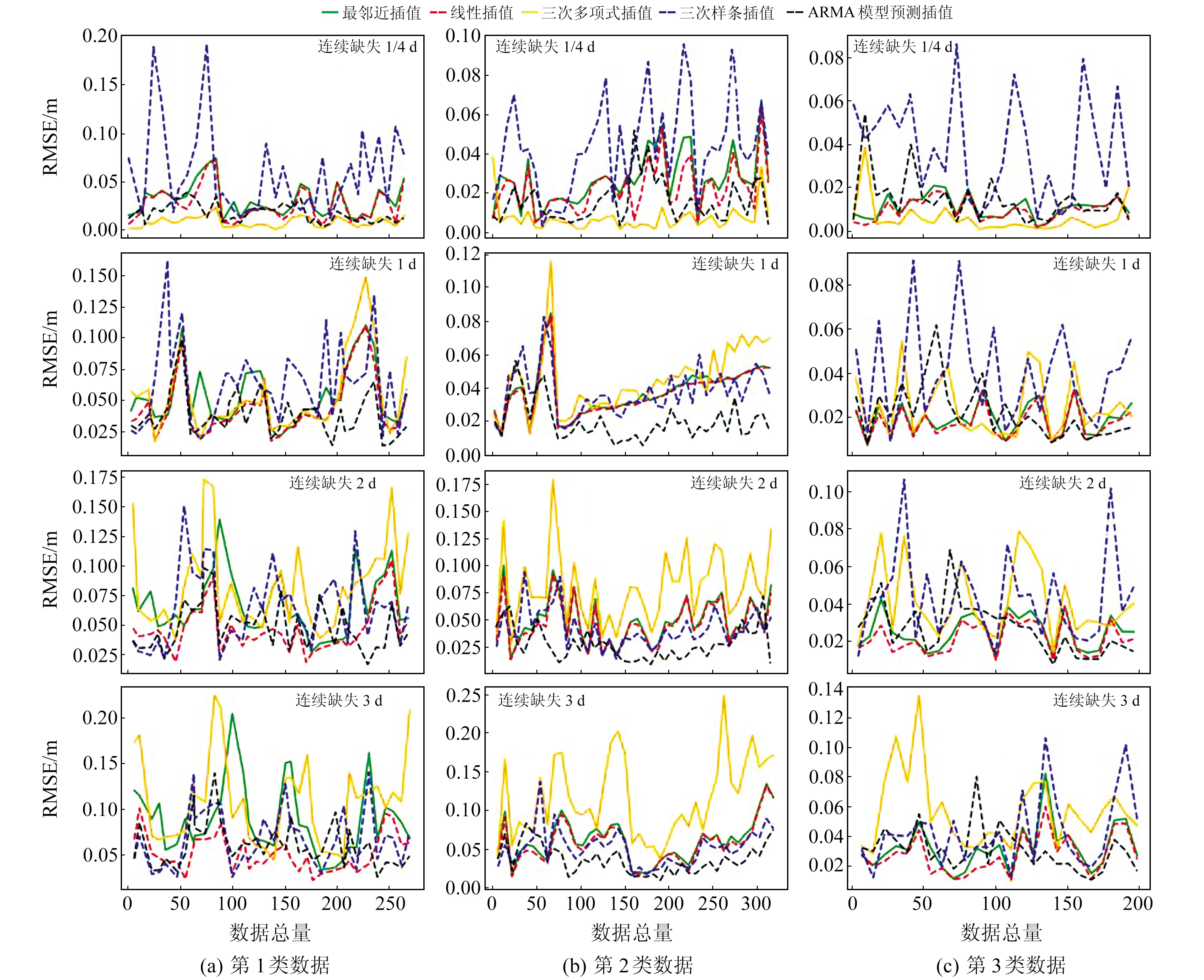
圖1 3類水位數據的RMSEFig.1 RMSE of three types of groundwater level data

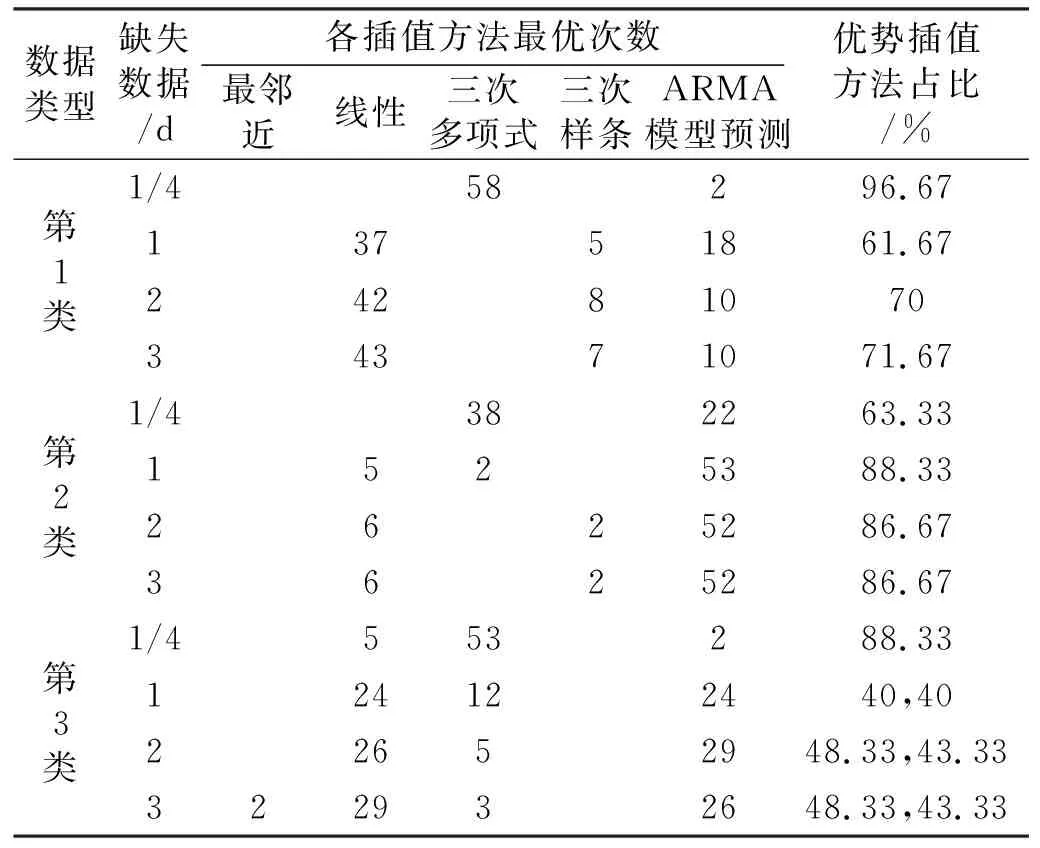
表2 最佳插值結果占比情況Tab.2 The proportion of the best interpolation results

最鄰近插值法與線性插值法的RMSE很相似(圖1)，但后者的優勢更突顯。三次樣條插值法的RMSE波動較大(圖1)，除對部分第1類數據外，其他插值RMSE都較大，但該方法對數據缺失量不敏感，不會隨缺失值增多而明顯增大。

2.3 回溯性檢驗

選取3類觀測井同一時段的12組數據，假設整點值缺1/4 d、1 d、2 d和3 d，計算5種插值法的RMSE，比較插值與觀測值曲線，檢驗上述結論是否正確。

對第1類水位數據(圖2(a)、表3)，當數據缺失1/4 d時，三次多項式插值法的RMSE為0.001 5 m，其插值結果更優。當數據缺失1 d、2 d和3 d時，線性插值法的RMSE分別為0.023 7 m、0.048 9 m和0.065 8 m，小于其他插值法結果。

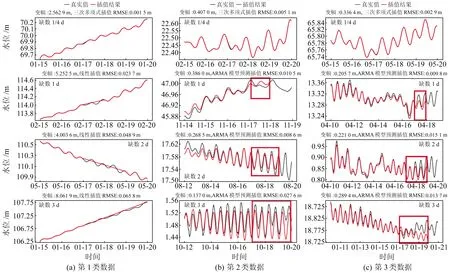
圖2 插值與觀測值對比Fig.2 Comparison of interpolation results and observed values

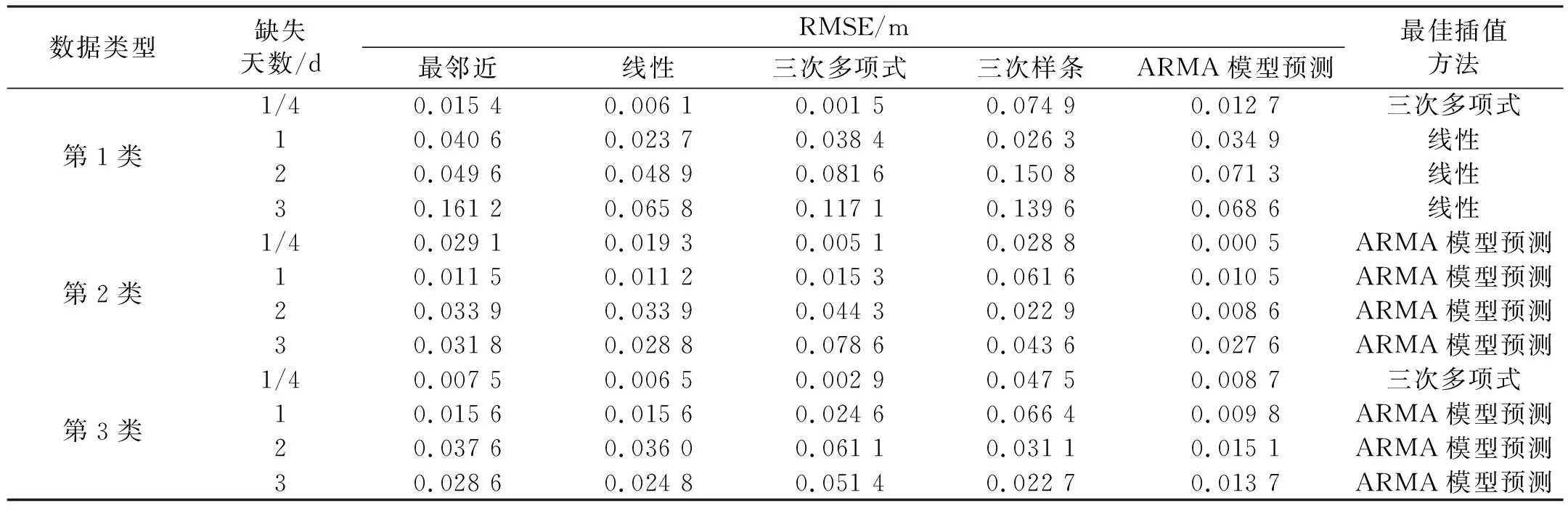
表3 3類水位數據的插值結果比較Tab.3 Comparison of interpolation results of three types of groundwater level

對第2類水位數據(圖2(b)、表3)，當數據缺失1/4 d和1 d時,ARMA模型預測插值法的RMSE分別為0.000 5 m和0.010 5 m，與三次多項式插值法RMSE的0.005 1 m和0.015 3 m相差不大；當數據缺失2 d時，ARMA模型預測插值法的RMSE遠小于其他插值法，插值優勢突顯；當數據缺失3 d時，ARMA模型預測插值法雖能還原潮汐波動周期，但很難還原波動幅度，與線性插值法的優勢相當。

對第3類觀測數據(圖2(c)、表3)，當數據缺失1/4 d時，線性、ARMA模型預測和三次多項式插值法的RMSE分別為0.006 5 m、0.008 7 m和0.002 9 m，三次多項式插值法更有優勢；當數據缺失1 d、2 d和3 d時，線性插值法與ARMA模型預測插值法的RMSE相近，但ARMA模型預測插值法的RMSE波動更小，插值結果更有優勢。

3 結 語

本文選取9口有固體潮效應的觀測井的180組水位數據，在不同缺值情況下進行5種插值方法的對比研究，得出以下結論：

1)三次多項式插值法對數據缺失1/4 d的插值RMSE小，且波動較小，其優勢占比分別為96.67%(第1類數據)、63.33%(第2類數據)和88.33%(第3類數據)，表明該插值法普遍適用于少量數據缺失的情況；

2)對趨勢變化大、固體潮效應被壓制的數據(第1類數據)，當數據缺失1 d、2 d和3 d時，線性插值法能延續數據趨勢變化，是最佳插值方法；

3)對固體潮顯著、趨勢變化平穩的水位數據(第2類數據)，當數據缺失1 d、2 d和3 d時，ARMA模型預測插值法能還原規則潮汐波動和單一趨勢的變化，插值最優比都在80%以上；

4)對固體潮汐明顯，又兼有起伏波動的水位數據(第3類數據)，線性插值法和ARMA模型預測插值法的優勢相當，線性插值法能還原趨勢變化，ARMA模型預測插值法能還原周期的潮汐波動。