地震數據采集器線性度不確定度評定及分析

鄭淑梅

1 中國地震局第一監測中心，天津市耐火路7號，300180

線性度是地震數據采集器的關鍵性能指標之一，可反映地震數據采集器輸出信號是否失真。評價線性度的常用方法有最小二乘法[1-3]和端基直線法[4]，地震數據采集器線性度計算多采用最小二乘法。

為評估最小二乘法和端基直線法對地震數據采集器線性度測量不確定度的影響，本文從理論上給出2種方法評價線性度的區別，通過實例展示不確定度的計算過程。最后通過對比多種型號的地震數采測量結果，分析2種方法的差別及不同輸入點個數和位置對線性度不確定度的影響。

1 最小二乘法和端基直線法的線性度理論

對于線性系統，輸入量x和輸出量y之間的關系為：

f(x)=kx+b

(1)

式中，k為直線斜率，b為直線截距。

用xi、yi(i=1,2,…,n)分別表示輸入值和測量值，則在信號點xi上測量值yi與線性回歸值f(xi)的殘差可表示為：

Δyi=yi-(kxi+b)

(2)

根據線性度定義，最大殘差可反映線性度大小。線性度公式為：

(3)

圖1為最小二乘法和端基直線法擬合示意圖。可以看出，二者計算線性度的區別在于k和b的估計值不同導致殘差Δy不同，殘差的正負和大小可表征測量值在擬合直線兩側的分散程度。按照最小二乘法原理，當殘差平方和最小時，k和b估計值最佳；端基直線法中，k和b只與首尾點有關。

圖1 線性擬合示意圖Fig.1 Schematic diagram of linear fitting

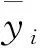
(4)

最小二乘法

(5)

(6)

2 測量不確定度模型

考慮到被測數據采集器的重復性和分辨力存在重復，合成不確定度時將二者中的最小值舍去。

根據不確定度理論公式[5]與文獻[1,4]可得，線性度L的合成標準不確定度為：

(7)

其有效自由度veff=m-3。

3 測量數據處理及分析

3.1 測量數據獲取及處理

采用標準源法，利用5730A輸出標準直流電壓信號作為地震數據采集器的輸入。選用EDAS-27HR型號地震數據采集器，測量范圍設為(-10 V, 10 V)，采樣率設為100 Hz，其A/D位數為28 bits，分辨率為0.149 μV/count。根據地震監測專業設備入網測試規程[6]選擇測試點，從-10～10 V每隔1 V選取1個點，首尾選取-9.5 V和9.5 V，共21個測試點。每個測試點測量2 min，截取20 s的數據計算其平均值，并將平均值折合到對應的輸入端作為最終的測量結果，由5730A標準儀器引入的不確定度分量u(Ei)采用B類評定，Ei的允許誤差極限由儀器說明書獲得。如參照5730A技術指標，測量2 V直流電壓時的擴展不確定度為5 ppm×Vout+0.7 μV，k=2，則其區間半寬為：

5.35×10-6V

在日常測量中，一般取2 000(20 s)個點的平均值作為測量結果，測量結果的實驗方差由式(4)獲得。最終的不確定度分量以及靈敏系數見表1。

對于最小二乘法，由式(2)和式(3)可得線性度估計值L=4.74×10-6，j=1。將表1中靈敏系數代入式(7)，計算得到最小二乘法線性度的合成標準不確定度為7.8×10-7V。

對于端基直線法，由式(2)和式(3)可得線性度估計值L=9.1×10-7，j=12。將表1中靈敏系數代入式(7)，計算得到端基直線法線性度的合成標準不確定度為6.5×10-7V，有效自由度均為veff=21-3=18。

表1 不確定度分量及靈敏系數Tab.1 Uncertainty components and sensitivity coefficients

3.2 測量數據分析

3.2.1 不同方法對計算結果的影響

分別采用最小二乘法和端基直線法對不同分辨力(數據位數)、不同型號的地震數據采集器的線性度結果進行不確定度評定，結果見表2。

從表2可以看出，最小二乘法與端基直線法線性度不確定度評定結果在同一數量級，與分辨力無關。因此，對于目前常用的地震數據采集器而言，無論采用最小二乘法還是端基直線法計算的線性度，其結果的離散度均很小。端基直線法線性度不確定度的評定結果較最小二乘法穩定，這主要與不確定度計算公式有關。

表2 最小二乘法與端基直線法線性度的標準不確定度Tab.2 Standard uncertainty of linearity of the least squares method and the terminal-based straight line method

3.2.2 數據點數和位置對計算結果的影響

為研究數據點數和位置對不確定度評定結果的影響，分別對19點、17點、15點、13點、11點、9點和7點數據在不同位置組合下線性度的不確定度進行評定。為不失一般性，仍然采用對稱的選點原則。如圖2所示，以19點數據為例，即在原21點數據的基礎上從大到小依次去掉對稱的一組數據，因此有9個位置組合。同理，17點、15點、13點、11點、9點和7點分別有8個、7個、6個、5個、4個和3個位置組合。2種方法在不同數據點及不同位置組合下的不確定度評定結果見圖3。

圖2 不同數據點數的位置組合示意圖Fig.2 Schematic diagram of the location combination of different data points

圖3 不同數據點數和位置對不確定度的影響Fig.3 The influence of different data points and locations on uncertainty

從圖3可以看出，最小二乘法線性度不確定度隨數據點數的增加而增加，其主要原因是不確定度計算公式為求和過程，數據點數越多其不確定度值越大。相對于最小二乘法，端基直線法線性度不確定度評定結果受數據點數影響較小，雖然不確定度的理論公式相同，但從靈敏系數可以看出，實際有效點數為3個值累加，因此其受數據點數的影響較小。

對于最小二乘法線性度不確定度而言，數據點數越多，對數據位置越不敏感；選取的數據越靠兩側，不確定度越小，說明靠邊的數據對不確定度的影響較大。端基直線法線性度不確定度均在末位位置組合處發生突變，這是因為除末位位置組合外，其他位置組合的最大殘差均在1 V點處出現，因此不確定度未發生任何變化，而末位位置組合已剔除1 V點，最大殘差點發生變化，因此出現不確定度不同程度的突變。

4 結 語

本文對地震數據采集器線性度不確定度進行評定，分析目前常用的最小二乘法和端基直線法線性度不確定度的差別。多種型號的地震數據采集器線性度不確定度評定結果表明，2種方法線性度不確定度評定結果在同一數量級，可以滿足地震數據采集器線性度不確定度評定的要求，但最小二乘法線性度不確定度受測試點數的影響較大，端基直線法線性度受測試點數的影響較小。