基于改進蟻群算法的農村運輸路徑規劃

黃二強，代永強，劉 歡

（甘肅農業大學信息科學技術學院，蘭州 730000）

0 引 言

隨著國家對環境保護的重視，農業得到了飛速發展，農產品的產量也有了全面提升，需要良好的交通運輸路徑來激活農村經濟。 因為國內地形地貌復雜多樣，各地的農村之間相距較遠、且農產品種類和產量也不相同，所以就需要規劃運輸路徑的軟件，來幫助規劃路徑，車輛運輸路線規劃已經變得越來越重要。 相對于常規的路徑規劃算法，首先，本文中的算法彌補了在運輸的整個環節中花費在農村收購點等待農產品的時間，因為地理原因，收購商到達農村收購點后，因為不同地區的果園或農田距生活區較遠，有的地勢陡峭、有的地質松散、比較危險，農民也會在不同的時間去采摘農產品，造成收購商額外花費的時間不同。 而常規的路徑規劃算法中只注重車輛調度花費的時間。 其次，本文中改進的蟻群算法融合退火算法后，提高了蟻群算法跳出局部最優的能力和收斂速度。 再次，通過融合蜜獾算法，在計算2 個收購點之間的距離時，本文考慮到農村地形影響因素，引入蜜獾算法在挖掘階段的心形模型來計算兩點間的距離，此模型更適合計算農村收購點之間的距離，其距離與實際路程更接近。 而常規算法是計算連點間直線距離，在計算山區中2 個農村之間的距離時，計算的直線距離與實際路程比本文中的要差。 本文選擇甘肅省若干個村鎮進行路徑規劃，利用改進的蟻群算法幫助收購商尋找一條最佳的運輸路徑。 運輸路徑規劃問題可歸于TSP［1］（traveling salesman problem）問題，在解決TSP 問題上，可用精確算法［2］或啟發式搜索算法［3］，如分層遞進的改進聚類蟻群算法［4］或者人工智能算法，如模擬退火算法［5］、蟻群算法［6］、禁忌搜索算法［7］、雞群算法［8］、粒子群算法［9］、蜂群算法［10］、麻雀搜索算法［11］以及遺傳算法［12］等。 在本文中用改進的蟻群算法來規劃車輛運輸路徑。 基于原始蟻群算法中跳出局部最優的能力低［13］、收斂速度慢［14］、優化效率低［15］的問題，改進的算法中，首先增加螞蟻體重突變的因素，可以提高蟻群的多樣性，從而提高蟻群算法跳出局部最優的能力。 在螞蟻體重突變的過程中，通過結合退火算法的概率計算方法來得到當前運動螞蟻的體重；其次，增加目標地點的時間權重參數，可通過設置目標點的時間權重值更快、更準確地找出下一個地點，提高了蟻群算法的收斂速度。 實驗結果表明，改進的蟻群算法有更好的尋優能力。

1 蟻群算法

蟻群算法是Dorigo 等學者［16］在二十世紀九十年代提出的一種新型的模擬進化算法［17］。 通過研究發現螞蟻之間傳遞信息是通過一種稱為信息素的物質，當螞蟻在尋找食物時通過這種物質進行信息交互的。 螞蟻在覓食的過程中會在經過的路徑上留下信息素，并且螞蟻也能夠感受到信息素，螞蟻會通過判斷信息素來指導自己運動的方向：若無信息素則按照隨機性前進，若有信息素、則根據信息素的強度來確定自己的運動方向。 螞蟻會選擇信息素、濃度高的方向運動。 由于大量螞蟻組成的蟻群集體行為表現出一種信息正反饋現象，在某一路徑上走過的螞蟻越多，則后來者選擇該路徑的概率就越大。蟻群算法相對于其他的一些算法很有優勢，文獻［18］中利用Matlab 對蟻群算法和遺傳算法對TSP的求解進行了研究對比，研究發現，在若干個城市里，無論兩地之間距離多遠，蟻群算法比遺傳算法更優。 在文獻［19］ 中設計了一種包含改進PRM（probabilistic road map）算法和蟻群算法的一種融合算法，可以一次規劃出多個目標點的路徑，但是所規劃出來的路徑具有隨機性。 文獻［20］中將蟻群算法和粒子群算法對比，蟻群算法的可靠性和精確度高、適應性強。在該算法中，將m只螞蟻隨機性地放在了n個城市里，全部的路徑（i，j） 上信息素的初始值△τij（0）＝常數（C），之后螞蟻k（1，…，m）在t時刻就按照其轉移概率來選擇出下一個節點。

2 模擬退火算法

模擬退火算法（Simulated Annealing，SA）最早的思想是由N. Metropolis 等學者［21］于1953年提出［21］。 1983年，Kirkpatrick［22］成功地將退火思想引入到組合優化［23］領域。 這是基于Monte－Carlo［24］迭代求解策略的一種隨機尋優算法［25］。 王光等學者［26］提出的算法進行可靠性模型參數求解，具有解的全局性好、收斂速度快等優點。 其出發點是基于物理中固體物質的退火過程與一般組合優化問題之間的相似性。 本質思想為以概率接受新狀態：在溫度為T時，設當前狀態為i，新狀態為j，若Ej ＜Ei，則接受j為當前狀態；否則，若概率大于［0，1） 區間的隨機數，則仍接受狀態j為當前狀態；若不成立，則保留狀態i為當前狀態。p ＝：在高溫下，可接受與當前狀態能量差較大的新狀態；在低溫下，只接受與當前狀態能量差較小的新狀態。 該式中的K為玻爾茲曼常量，是熱力學的一個基本常量，數值為1.380 649×10－23J／K。

3 蜜獾算法

蜜獾算法（Honey Bavdger Algorithm，HBA）是2022年提出的一種元啟發式優化算法。 該算法的靈感來源于蜜獾的覓食行為，蜜獾會通過挖掘階段和采蜜階段尋找食物，還會根據氣味強弱接近獵物捕食。 該算法具有開發能力強、收斂速度快等特點，但探索能力有所不足。 研究發現，蜜獾算法的挖掘階段的心形模型類似于農村收購點之間的路線形狀，故而將蜜獾算法融合到農村收購點路徑優化算法中。

4 改進的蟻群算法

針對蟻群算法收斂速度慢的問題，先提出對原始蟻群算法［27］的信息素優化方法，其次討論了改進的蟻群算法的原理。

4.1 信息素的優化

首先，在改進的蟻群算法中對參數信息素重要程度α和信息素啟發式因子β進行多次實驗得到的最優值并將其參數值都設置為最優值2。 其次，根據蟻群生物學［28］了解到蟻群中由工蟻、兵蟻、雄蟻、蟻后等組成，其中在工蟻或兵蟻或雄蟻中的螞蟻的個體大小和體重并不一樣，而其中更重的螞蟻對信息素時的釋放量比更輕的螞蟻釋放得更多，由此引入螞蟻的體重突變因素不僅增加了蟻群的多樣性，而且間接地影響了螞蟻釋放信息素的量；在原始蟻群算法中，信息素的釋放量是一個常量，而在改進的蟻群算法中將其信息素改為可變的量。當一只螞蟻從i點到j點，若從i點到j點的路徑不是最優路徑時，由于越來越多的螞蟻的移動將由信息素來進行導向，那么從（i，j） 路徑上走過的螞蟻就越來越多，導致蟻群算法跳出局部最優的能力越差。 根據下文函數（8）可以看出，可以通過蒙特卡洛準則中的概率公式得到螞蟻體重突變概率F，進而可以得到該螞蟻的體重，因為下一個農村點的時間權重值越大，則該地點需要等待的時間越長，而兩地時間權重值的差值越大，則函數（8）得到的概率值F就越小，再通過下文函數（5）可以看出，F越小、則螞蟻體重突變的概率越小，進而該螞蟻釋放的信息素就越少，反之則釋放的信息素越多，最終提高了蟻群算法跳出局部最優的能力，加快了算法的收斂速度。

4.2 算法介紹

將m只螞蟻隨機性地放在了n個城市里，路徑（i，j） 上信息素的初始值τij（0）＝0，螞蟻k（1…48）在t時刻按照其轉移概率來選擇出下一個節點。 通過多次實驗測試得出，信息素重要性α的值和啟發式因子β的值分別設置為2和2，將螞蟻的體重突變作為影響啟發式因子的因素，螞蟻的體重越大，且當前路徑的距離越短，啟發信息越大，則選擇此路徑的可能性越大；實驗測試得出，改進蟻群算法的收斂速度更快、得到的解更優。 由此推得的公式為：

其中，Lij表示通過蜜獾算法的挖掘模式計算得到農村山區路段（i，g，j）的距離，s表示螞蟻通過體重突變后的體重。 函數（2） 中考慮到山區地形因素，引入了車輛體重因素對道路順暢度的影響：車體越重的、主要考慮路線長短的因素，次要考慮時間長短的因素。

各個路徑所含的信息素更新公式為：

其中，1－ ρ表示信息素殘留因子，ρ∈（0，1）。

其中，△τij表示在本次所有螞蟻運動到目的地時，路徑（i，j） 上螞蟻的信息素總量； 在初始時刻△τij（0）＝0，指的是第k只螞蟻在此次循環時留在路徑（i，j） 上的信息素總量。 此處需用到如下公式：

首先，從函數（5）中可以看出在信息素釋放量的影響因素中添加了車輛重量因素，其車重超出標準越多、且路程越長時，路段（i，j） 上釋放的信息素就越少，選中該路段的概率就越小，反之則概率越大。 其次，是通過蜜獾算法中挖掘階段的心形模型計算兩點之間的路程，通過該模型得到的路程更符合實際情況：

在實際情況中考察得知，農村收購點之間需要翻過山丘或者大山，其路程是弧形的、與蜜獾算法的挖掘階段的心形模型類似，在螞蟻搜尋的初始階段按照蜜獾算法中的挖掘階段的模型找到一個隨機產生的坐標（xg，yg，），可以通過該模型計算2 個農村收購點（i，j） 之間的實際距離為（i，g，j），算法如下：

其中，xg為模型在經度上的弧度；yg為模型在緯度上的弧度；α、r0、r1、r2為（0，1）的隨機數。

在此基礎上，又推得數學模型公式具體如下：

5 模型構建及求解

5.1 選取48 個農村點

在甘肅省內選擇48 個農村種植區的經緯度作為坐標，通過改進的蟻群算法進行路徑規劃。 選取的農村種植區的坐標見表1。

表1 農村坐標表Tab. 1 Rural coordinates

5.2 問題分析

商貿企業在經營過程中以效益為首，需要開源節流，而運輸過程中消耗的時間和資源是商貿企業支出的重要的一部分，通過對商貿企業運輸車輛的路徑規劃可以讓商貿企業減少開支。 商貿企業在采購農產品時，首先，為了減少不必要的車程開銷，假設運輸車輛從一個農村點出發、從所有農村點只經過一次。 直至到達最后一個農村點的前提下，規劃出路程最短的最優路徑，類似旅行商問題。 本文利用改進的蟻群算法求解運輸路線的最優路徑。 其次，以收購農產品為例，計算所需天數。 不妨假設從平涼.焦莊村出發，經過所有農村點、直到最后一個農村點，花費的時間包括運輸車輛在路上的時間和在農村點等待收購所花費的時間；根據前面求解出的最佳運輸路徑，計算出所需的天數，并且對運輸過程做具體的安排。

5.3 求解實例與仿真

改進的蟻群算法給參數設定的值可以應用到農產品運輸路徑規劃中，首先在時間權重T ＝1 時對運輸路線進行規劃，其次時間權重T的值分別按3種方案對運輸路線進行規劃。 通過實驗得到各地點在3 種時間權重情況下的運輸路徑規劃結果。

5.3.1 算法對比

首先，繪制出48 個農村點的坐標，如圖1 所示。其次，當時間權重值T ＝1 時，求出原始蟻群算法和改進的蟻群算法在200 次測試中每一次得到的最優路徑長度，如圖2 所示。 最后，通過對表2 中的2 種算法在最優解、平均解和耗時三方面做對比，可以看出改進的蟻群算法收斂速度更快、跳出局部最優的能力更強、得到的解更優，并繪制出改進的蟻群算法求解得到的最優路徑圖，并進行2 種不同的展示，如圖3、圖4 所示。

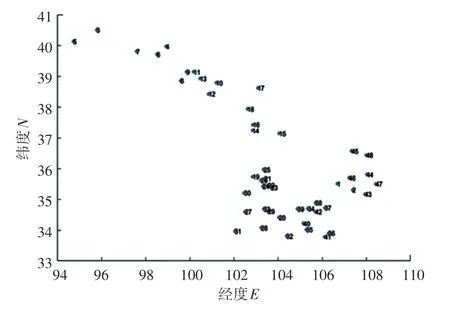
圖1 48 個地點分布圖Fig. 1 Distribution of 48 sites

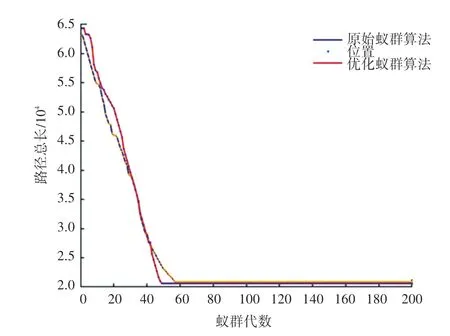
圖2 各地時間權值T ＝1 時的路徑曲線圖Fig. 2 Path curve when time weight T ＝1

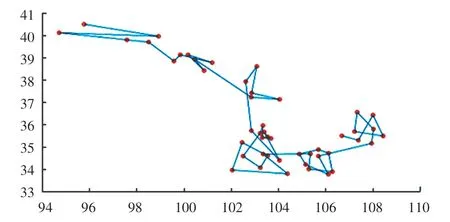
圖3 無經緯度的最優路徑Fig. 3 Optimal path without longitude and latitude

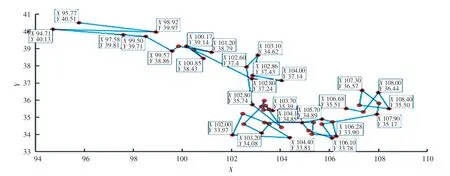
圖4 有經緯度的最優路徑Fig. 4 Optimal path with longitude and latitude

表2 算法比較Tab. 2 Comparison of algorithms

5.3.2 設置時間權重表

從往年的收購花費時間的記錄中可以預估兩地之間從出發到完成農產品收購需要花費的天數、即時間權重，在3 種不同的天氣給48 個農村點設置時間權重值T；T ＝1 指的是運輸車輛到達農村時、可以立即開始收購農產品，值為1.5、表示需要等待0.5天才可以收購農產品，其余值依此類推。

5.3.3 求最優路徑

在改進的蟻群算法中，根據表3～表5 三個方案的時間權重值分別求出對應的最優路線。 經過200 次測試，得到運輸車輛的3 種最優路徑，如圖5～圖7 所示。3 種策略得到的曲線如圖8 所示。 根據圖8，可以看出3 條路線的收斂速度、及最優路徑的路徑總長。 車輛央最優路徑上花費的時間的結果曲線如圖9 所示。 根據圖9，可以看出每輛車經過全程所花費的時間。

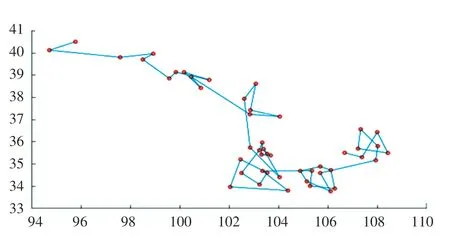
圖5 根據表2 得到的最優路徑Fig. 5 The optimal path obtained according to Table2

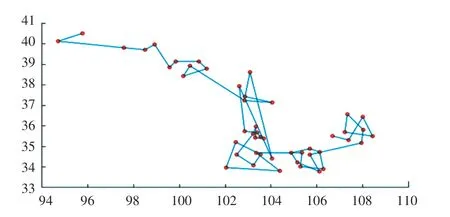
圖6 根據表3 得到的最優路徑Fig. 6 The optimal path obtained according to Table3

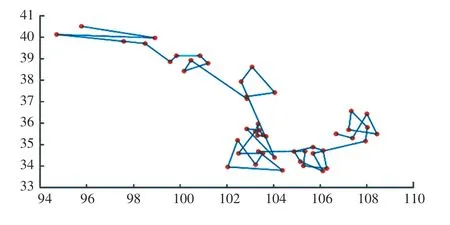
圖7 根據表4 得到的最優路徑Fig. 7 The optimal path obtained according to Table4

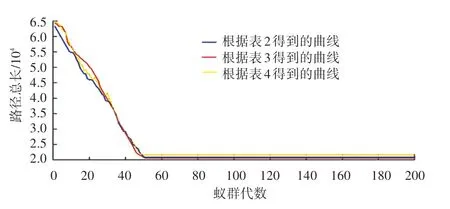
圖8 3 種策略得到的曲線Fig. 8 Curves obtained by three strategies

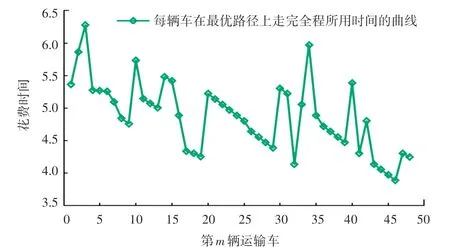
圖9 車輛在最優路徑上花費時間的曲線Fig. 9 Curve of time spent by vehicles on the optimal path

表3 方案一的各地的時間權重值Tab. 3 Time weight value of each region in scheme I

表4 方案二的各地的時間權重值Tab. 4 Time weight values of different regions in scheme II

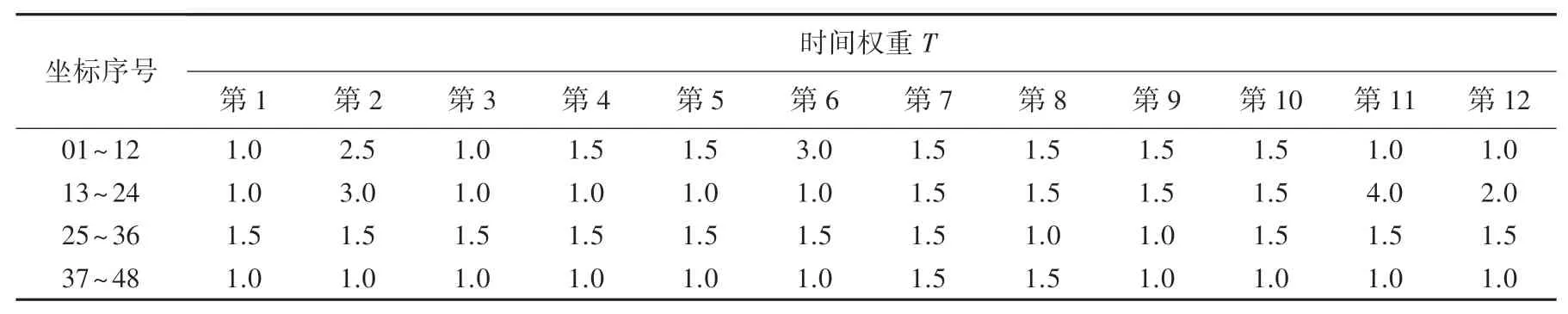
表5 方案三的各地的時間權重值Tab. 5 Time weight values of different regions in scheme III

5.3.4 規劃路徑的建議

從圖5～圖8 看出，可以通過設置時間權重來規劃出路徑方案，該方案可以在花費最少的時間、農產品價格最低、成熟度最好時，到達各農村收購和運輸農產品，通過這種方法可以消耗最少的資源來得到最大的收益。 從圖8 中可以看出紅色曲線的運輸規劃路徑在地理順序和路程總長兩方面是最優的運輸路徑。 經過這48 個農村的最佳運輸路路徑為：2—1—3—4—5—6—7—10—8—9—11—15—13—14—12—16—18—17—21—20—19—22—23—26—25—27—28—30—29—33—36—30—31—32—34—35—39—37—47—42—44—38—45—48—46—43—41—40。 花費總時間：3.888 9 天，實際上就是需4 天。

行程安排：要完成這些村鎮的農產品的收購工作，總共需要4 天。 如果企業安排收購任務的時間比較寬裕，可以在符合時間范圍內的規劃路徑中將天氣等因素考慮其中，如此就可以更完美地規劃運輸路徑了。

6 結束語

本文提出了一種改進的蟻群算法，并將其應用到農村運輸路徑的優化求解。 首先，在基本蟻群算法中引入了模擬退火算法的隨機概率作為螞蟻體重突變的策略的參數和時間權重參數，使算法更快地跳出局部最優；采用螞蟻體重突變策略增強了種群的多樣性，提高了全局搜索能力和算法的收斂速度。 其次，根據農村運輸的環境建立模型，并建立目標函數。 最后，通過Matlab 進行仿真實驗，結果表明優化蟻群算法能夠更快速地找出最優路徑以及在運輸過程中花費的時間，有效提高了運輸路徑規劃的效率。 運輸路徑規劃受環境的影響較大，本文開展的研究未考慮天氣、高山等環境因素的影響，在以后的研究工作中將增加其他影響運輸路徑規劃因素進行系統研究。