基于SVR 數據中心空調系統瞬態熱參數預測

黃金森，朱 兵，張一鳴，殷佳輝，苗益川

（貴州大學電氣工程學院，貴陽 550025）

0 引 言

截至2021年，中國數據中心機架總規模超過520 萬，在用服務器規模達到1 900 萬臺，預計未來國內數據中心裝機容量將繼續保持快速增長［1］。龐大的裝機容量使得數據中心行業用電量飛速增長，預計到2025年國內數據中心用電量將達到3 950億千瓦時，占全社會用電量的5.8%［2］。 Ni 等學者［3］調查了100 個數據中心能耗情況，暖通空調系統能耗占總能耗平均值為38%，其中，在調查的能耗最低占比為21%，最高占比為61%，可見數據中心空調系統節能潛力巨大。 僅通過改造機房結構進行氣流組織優化的傳統措施已不能滿節能需求，在此基礎上開發動態優化冷源供應控制系統是目前行業的迫切需要，而建立動態優化供冷控制系統首要任務是實現數據中心氣流組織熱參數的快速預測。 Athavale 等學者［4］評估了人工神經網絡（ANN）、高斯過程回歸（GPR）和支持向量回歸（SVR）3 種機器學習方法對數據中心穩態工況下機架入口溫度分布的預測性能，研究表明三種方法所得到的穩態模型具有相當的準確性，對于冷卻故障情況下的瞬態預測，核函數的選擇決定了SVR 和GPR 所開發模型的外推能力。 本文使用帶線性核函數的支持向量回歸機對空調故障情況下熱參數進行預測。

1 實驗數據分析

空調系統冷凍水泵故障是數據中心日常運行中常見的故障情況之一，在實驗室RL［5］中進行空調冷凍水泵故障實驗和風機故障實驗。 實驗過程中，在每個模擬機箱的入口設置了9 個測溫點，10 塊高架地板每塊上方設置一個測溫點，空調回風口設置6個測溫點，空調出風口設置4 個測溫點，每個測溫點布置1 個熱電偶測溫，取每個位置所有熱電偶的平均值，實驗溫度測量的不確定度約為0.5～1 K。

1.1 冷凍水泵失效實驗

冷凍水泵失效實驗研究了冷凍水泵失效后6 min內高架地板入口，空調回風口、空調進風口、每個模擬機箱入口的溫度變化，實驗中為了避免實驗設備損壞，在R1、R2、R3 負荷均為20%的條件下進行實驗，在服務器及空調穩定運行過程中關閉，冷凍水回水閥，從關閉時開始約60 s 冷凍水回水閥完全關閉冷凍水泵停止運行時間總計6 min。 在此期間，測量了空調回風溫度、空調出風溫度、高架地板入口溫度等參數。 機房及靜壓箱內的空氣循環如圖1 所示。

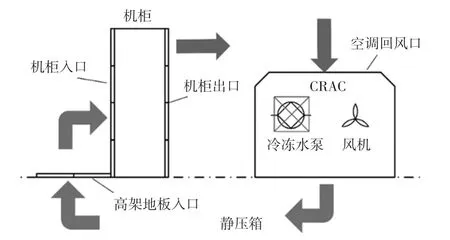
圖1 機房及靜壓箱內的空氣循環示意圖Fig. 1 Schematic diagram of air circulation in the equipment room and plenum

在冷凍水泵失效的6 min 內空調回風溫度、空調出風溫度、高架地板入口溫度與模擬機箱R1C4的入口溫度變化情況如圖2 所示。 冷凍水泵停止運行意味著從機房進入空調的熱風無法被循環水冷卻，只能與滯留在換熱器內的冷凍水進行熱交換，由于此時冷凍水處于靜止狀態，換熱系數較低，因此空調的時間常數比正常運行情況下更長、約為70 s。由于風機正常運行，所以機房內流場未發生較大變化，空調的出風溫度逐漸上升，最終接近于空調回風溫度。 高架地板的出風溫度曲線與空調出風溫度曲線出現交叉，在40 s 左右空調出風溫度超過高架地板出風溫度，空調出風溫度上升速度高于高架地板出風口的溫度，這是因為靜壓箱內混凝土底板、側墻等建筑材料比熱容比空氣大，在靜壓箱內空氣溫度迅速升高時起到了冷卻作用。 模擬機箱R1C4 進風溫度變化趨勢與空調回風溫度變化趨勢大致相同，在0 ～50 s 區間內溫度變化較小，這是因為冷源失效的初始時刻靜壓箱內儲備了一定量的冷空氣，因此仍可以維持一定時間的制冷效果；50 s 后基本呈線性增長趨勢，此時由于靜壓箱內儲備的冷空氣逐漸耗盡，在服務器的加熱作用下，機房內空氣循環的平均溫度逐漸升高。

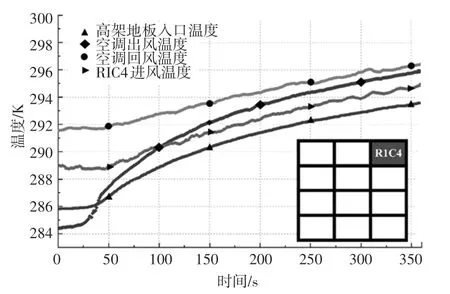
圖2 水泵失效期間機房部分位置溫度變化圖Fig. 2 Temperature variation of some parts of the equipment room during water pump failure

1.2 空調風機失效實驗

空調系統冷風扇故障同樣是數據中心日常運行中常見的故障情況之一，為了避免實驗設備損壞，風機失效實驗在R1、R2、R3 負荷均在30%的條件下進行，在服務器及空調穩定運行過程中關閉空調風機停止運行時間總計6 min。 在此期間沒有新風進入機房，模擬機箱入口循環吸入自身排氣。 實驗測量了R3C4、R2C4、R1C4、R1C3 共4 個模擬機箱的入口溫度變化，4 個模擬機箱的入口溫度變化情況相差不大。 圖3 展示了在空調風機失效的6 min 內模擬機箱R3C4 和R1C4 的入口溫度變化情況。 在風機失效后的360 s 內，模擬機箱R1C4 與R3C4 的變化趨勢大致相同： 在風機失效后的0 ～180 s 區間內，機柜入口溫度約上升了12 K；在180～360 s 區間內，機柜入口溫度約上升了5 K。 溫度變化呈現出先快后慢的趨勢，這是由于風機失效后，空調出風流量逐漸減小，靜壓箱與機房之間的壓差逐漸消失，冷風無法穿過高架地板進入機房。 此時由于冷卻不足，模擬機箱不斷循環吸入自身排氣，使得機柜內部溫度不斷升高，入口溫度迅速上升。 與此同時，機柜入口空氣流速降低導致邊界層厚度增加，湍流程度降低，從而使空氣對流換熱系數降低，隨著溫度的上升空氣與服務器之間的溫差降低，溫度上升速度減小。

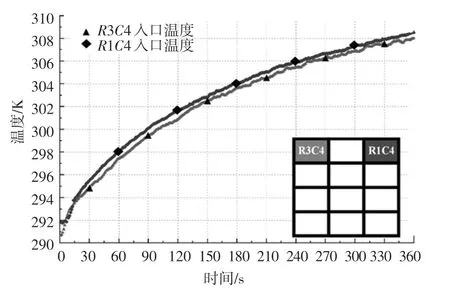
圖3 風機失效期間R3C4 及R1C4 入口溫度變化圖Fig. 3 Temperature variation of R3C4 and R1C4 inlet during fan failure

2 時間序列預測簡介

時間序列預測原理是根據某個變量的歷史變化情況對該變量在未來某段時間或某個時刻的變化情況做出預測。 時間序列預測不局限于對未來值的預測，還包括異常檢測時間序列分類等領域。 時間序列也叫時間數列、歷史復數或動態數列，是在某一時間區間內按順序記錄下的相同指標的數據集合，具有可比性。 常見的時間序列預測模型有時間分解、自回歸（AR）模型、移動平均（MA）模型、自回歸滑動平均（ARMA） 模型、 差分自回歸移動平均（ARIMA） 模型、帶輸入差分自回歸平均移動（ARIMAX）模型等，然而由于AR、MA、ARMA 模型特性，三者只適合對平穩時間序列進行線性擬合，當處理的時間序列呈現上升或下降的趨勢時預測效果不盡人意。 因此ARIMA 模型應運而生，該模型通過對不平穩的時間序列進行差分或對數化運算，將其轉化為平穩時間序列后對其進行自回歸滑動平均分析［6］。 ARIMAX 則是在ARIMA 的基礎上實現了基于輸入變量時間序列預測。

隨著計算機技術的飛速發展推動了機器學習和深度學習等建模方法的迅速崛起，相較于傳統時間序列預測模型，機器學習模型非線性擬合能力更強，可以對超大維度及變化復雜的時間序列數據進行處理。 支持向量回歸機在處理小樣本數據時相較于其他算法更有優勢，且空調冷凍水泵停機后溫度變化接近線性，因此與文獻［4］使用的非線性核函數支持向量機不同，本文使用基于線性核函數的支持向量回歸機對空調系統失效時機房內溫度變化情況進行預測，實驗樣本數量為360 組，是空調失效360 s 內關鍵位置的溫度變化情況，每秒記錄一次。 在空調失效的360 s 內，前180 s 的數據用于模型訓練，后180 s 的數據進行外推預測。 時間步長設置為15 s，單時間步預測，即使用某點前15 個數據對其進行預測，對實驗數據進行滑窗處理，將訓練集輸入整理為15 個數據為一組，時間序列的實現過程見圖4。

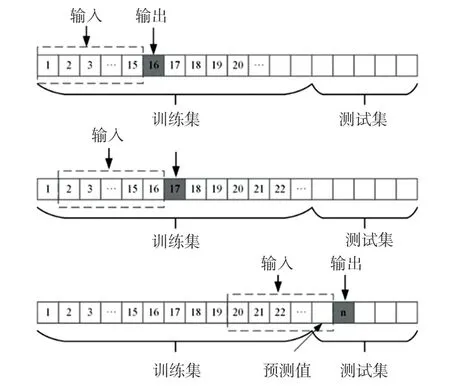
圖4 時間序列外推預測示意圖Fig. 4 Schematic diagram of time series extrapolation prediction

3 基于SVR 的時間序列預測

3.1 冷凍水泵失效參數預測

如前文所述，前180 s 的數據用于訓練模型，后180 s 的數據用于測試外推精度，檢驗支持向量回歸模型對時間序列的預測精度。使用帶線性核函數的支持向量回歸機對空調回風溫度及R1C4 模擬機箱入口溫度進行預測。

3.1.1 空調回風溫度預測

冷凍水泵停機后，空調回風溫度實驗值與預測值對比結果如圖5 所示。 預測值與觀測值在360 個觀測點的誤差分布如圖6 所示。

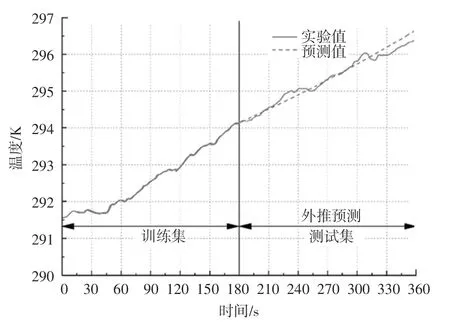
圖5 空調回風溫度時間序列預測結果Fig. 5 Time series prediction results of air conditioner return air temperature

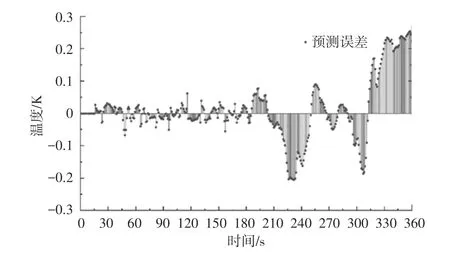
圖6 空調回風溫度時間序列預測誤差Fig. 6 Time series prediction error of air conditioner return air temperature

從圖5 和圖6 中可以明顯看到，在16～180 s 的區間內（由于時間序列的滑動窗口長度（時間步長）為15，因此前15 s 的數據不作為參考），時間序列訓練集吻合效果較好，最大絕對誤差小于0.1 K。 在180～360 s 區間內，預測結果可以準確反映溫度變化的總體趨勢，但線性模型無法反映實際測量結果的輕微波動，空調回風溫度預測模型評價指標見表1。

表1 空調回風溫度預測評價指標Tab. 1 Evaluation index of air conditioner return air temperature prediction

從評價指標看，外推預測的最大絕對預測誤差為0.255 K，均方根誤差為0.062 7 K，均遠小于空調回風溫度的測量不確定度1 K。 模型訓練時間約為1 s，可以認為線性核函數支持向量機在180～360 s 外推區間內實現了對空調回風溫度的快速準確預測。

3.1.2 R1C4 模擬機箱入口溫度預測

冷凍水泵停機后模擬機箱R1C4 入口溫度實驗值與預測值對比結果如圖7 所示。 預測值與觀測值在360 個觀測點的誤差分布如圖8 所示。

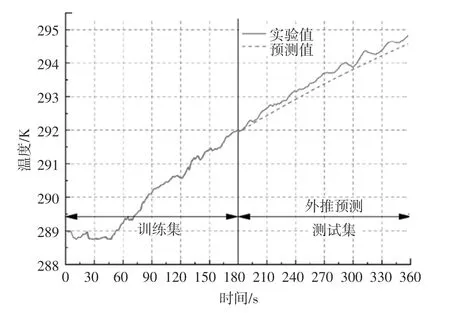
圖7 模擬機箱R1C4 入口溫度時間序列預測結果Fig. 7 Time series prediction results of inlet temperature of simulated chassis R1C4

圖8 模擬機箱R1C4 入口溫度時間序列預測誤差Fig. 8 Prediction error of inlet temperature time series of simulated chassis R1C4

從圖7 和圖8 中可以明顯看到，在前180 s 訓練集內支持向量回歸機預測值與觀測值總體擬合良好，誤差隨著曲線的波動小范圍內變化。 在180 ～360 s 區間內，預測值均小于實驗值，外推預測誤差隨曲線波動變化，平均誤差逐漸增大。 從變化趨勢看，在360 s 之后的預測值精度將難以保證，模擬機箱R1C4 入口溫度預測模型評價指標見表2。

表2 模擬機箱R1C4 入口溫度預測評價指標Tab. 2 Evaluation indexes of inlet temperature prediction of simulated chassis R1C4

從評價指標來看測試集的各項誤差均大于訓練集，測試集均方根誤差為0.218 K，最大誤差為0.382 K，均小于實驗測量的不確定度，且模型訓練時間小于1 s，因此可認為實現了較為準確的快速溫度預測。 測試集相關性相較于訓練集明顯下降，這主要是實驗值曲線波動較大造成的。 在氣流組織變化較快的位置，預測模型準確性會有所降低。

根據本文中空調回風溫度預測模型、模擬機箱R1C4 入口溫度預測模型的評價指標對比文獻［4］中研究成果，可以發現與非線性核函數支持向量機相比，線性核函數支持向量機更適用于冷凍水泵失效時的熱參數預測，因為在冷凍水泵失效后的短期內機柜入口溫度變化趨勢及空調回風溫度變化趨勢接近線性。

3.2 風機失效參數預測

冷凍水泵停機后空調回風溫度實驗值與預測值對比結果如圖9 所示。 預測值與觀測值在360 個觀測點的誤差分布如圖10 所示。

圖9 模擬機箱R3C4 入口溫度時間序列預測誤差Fig. 9 Prediction error of temperature time series at the entrance of the simulated chassis R3C4

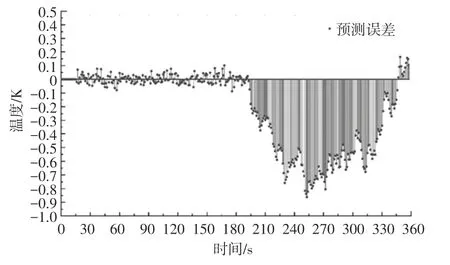
圖10 模擬機箱R3C4 入口溫度時間序列預測誤差Fig. 10 Prediction error of temperature time series at the entrance of the simulated chassis R3C4

從圖9 和圖10 中可以明顯看到，在前180 s 訓練集內支持向量回歸機預測值與觀測值總體擬合良好，誤差隨著曲線的波動小范圍內變化。 在180 ～310 s 外推預測區間實驗值并非嚴格線性變化，并且實驗數據有一定的噪聲，造成預測誤差較大。 預測值在180 ～345 s 內預測值均低估了實驗值，隨著實際溫度上升速度下降，預測值與實驗值出現相交，可以看出在360 s 之后預測值將不斷增長，預測結果將不再可信，模擬機箱R1C4 入口溫度預測模型評價指標見表3。

表3 模擬機箱R3C4 入口溫度預測評價指標Tab. 3 Evaluation indexes of inlet temperature prediction of simulated chassis R3C4

從評價指標來看，測試集的誤差遠大于訓練集，最大誤差達到0.862 K，均方根誤差為0.496 K，且測試集的相關性不高，R2約為0.85。 此外，由于模型的懲罰因子較大，訓練時間約為6 s。 這是因為當風機失效后，機柜入口溫度變化趨勢與冷凍水泵失效后不同，溫度上升速度先快后慢，機柜入口溫度變化趨勢呈非線性，因此線性核函數支持向量機的預測結果不夠理想。

4 結束語

根據Erden［5］在RL 實驗室進行的空調系統故障實驗分別建立了空調冷凍水泵失效時的空調回風溫度預測模型與模擬機箱R1C4 入口溫度預測模型及風機失效情況下模擬機箱R3C4 入口溫度預測模型。 3 個模型均基于線性核函數支持向量回歸機，冷凍水泵失效時的空調回風溫度預測模型和R1C4入口溫度預測模型，在180 ～360 s 區間內均實現了較為準確的快速外推預測，均方根誤差分別為0.063 K、0.218 K，但風機失效時的R3C4 入口溫度預測模型表現不夠理想，外推預測均方根誤差為0.049 6 K，但最大預測誤差達到0.862 K，其原因是風機失效后的機柜入口溫度上升速度逐漸減小，變化趨勢呈非線性特征，如果有關于溫度變化趨勢的先驗知識，通過選擇一個線性增長的核函數來提高基于SVR 的模型的外推能力。 研究表明了相較于非線性核函數支持向量機，線性核函數支持向量機更適合進行冷凍水泵失效時的熱參數預測。