公交停靠站多線路換乘協同調度

趙新標，劉心雨，夏曉梅，項俊平，趙 靖

（1 上海理工大學管理學院，上海 200093； 2 連云港杰瑞電子有限公司，江蘇 連云港 222006）

0 引 言

隨著城市交通的不斷發展，出行需求和公交方式逐漸多樣化，使得公交網絡呈現多模式層級化結構。 然而，在多線路公交運行過程中，當在同一站點的不同線路之間相互換乘的需求都較大時，常規調度策略難以同時滿足該站點所有線路的乘客換乘需求，從而導致乘客換乘候車時間長，公交服務水平低，最終造成公交分擔率下降的現象。 因此，高效合理的多線路協調調度策略是提高公交服務水平的必要條件。

公交多線路協同調度問題一直是交通領域的一個研究熱點，國內外許多學者都進行了深入的探討與研究。 國外學者對此研究相對較早，2012年Ibarra－Rojas 等學者［1］提出了一個重要的觀點，研究認為2 輛公交車行程到達換乘點時間的差值在給定時間窗口內，則即可認為這2 個行程是同步的。 自此以后，關于最大化多線路換乘同步次數的研究多是基于此觀點，并在此基礎上不斷創新。 2016年，Wu 等學者［2］認為對現有發車時刻表進行較大的修改，不僅破壞乘客習慣的出行計劃，還導致后續調度任務的大量重新計算。 因此，提出一種多目標方法，允許決策者考慮在每個特定的時刻表同步水平上可以接受的與現有線路發車時間的偏差。 2022年，Renzo 等學者［3］用Virtual Savant 新型軟計算方法，將機器學習和優化相結合，解決了最大化公交同步次數的問題。 研究還將節點不僅僅考慮為固定的公交車站，而是整個換乘區。 2023年，Ansarilari 等學者［4］將公交容量約束納入換乘時間優化模型，獲得更現實的解決方案。 國內學者同樣對此展開了深入研究，在2003年鄒迎等學者［5］已經分析了單線調度模式存在的弊端，提出多線路運營組織與調度的基本設想，并深入探討了區域調度應用的可行性及具體實施框架。 隨后，2007年石琴［6］及2014年黃義［7］等以最大化不同公交線路車輛在換乘站點的總相遇次數為目標，從而實現線路間乘客的同步換乘。 直至2016年，楊信豐等學者［8］同樣提出在公交調度過程中很難做到有換乘關系的車輛同時到達換乘站點，而乘客在一個允許的時間區間內實現換乘與實際更相符。 2018年，洪豆［9］對公交共線路段上的運力資源配置問題展開了研究，提出考慮共線路段的公交調度模型更具實用價值。 2020年，高姝敏［10］著重考慮了車輛容量限制，并對因容量限制而未能上車的乘客進行分析，分情況討論滯站乘客類型及其額外候車時間。 2020年，趙靖等學者［11］將需求響應型公交行車調度運用至社區公交中，提出一種新的響應型社區公交，統籌考慮需求起訖點、需求等級、動態需求，有效減少了乘客的等待時間以及步行距離。 2022年，韓印等學者［12］將快速公交車輛調度與沿線交叉口信號配時進行了協同優化，并基于客流時空分布不均衡的特征，綜合考慮了全程車、大站快車、區間車等多種調度模式。 2023年，趙靖等學者［13］利用車牌識別數據，根據不同流向，提取了不受信號延誤影響的車輛路段行程時間分布，并在此基礎上，建立了考慮行程時間波動的干線信號協調控制魯棒優化模型，有效提高了綠波帶寬。

目前，在最大化公交多線路同步次數方面具有較為豐碩的成果，但若是僅關注公交多線路同步次數，確實可以提高乘客換乘效率，縮短乘客換乘時間，卻也忽略了無需換乘的乘客的出行需求，公交多線路同步次數的增加，并不意味著乘客平均行程時間會減少。 此外，面對多線路互相換乘的需求較大的情況，現有學者所提出的多線路同步方法，即促使兩輛公交車到達換乘點時間的差值在給定時間窗口內，是無法滿足多線路乘客相互換乘的需求的。 原因在于一旦2 條線路的公交車離開換乘站點存在先后順序，就僅有先到站的公交車輛上的乘客可以換乘成功，而后到站的公交車輛上的乘客則需等待換乘目標線路的下一輛車輛。 因此，基于上述問題，本研究以乘客平均行程時間最小為目標，考慮發車間隔與駐站時間的限制，對車輛的發車間隔以及在換乘站點的駐站時間進行優化，延長先到站車輛在換乘站點的駐站時間，促使先到站車輛可在換乘站點等待有換乘關系車輛，使得兩輛非同時到達換乘站點的公交車依然可以同時離開站點，實現多線路乘客相互換乘。

1 模型建立

1.1 模型構建

本研究旨在對公交的發車間隔以及在換乘站點的駐站時間進行優化，提高換乘效率，縮短乘客出行時間，因此以乘客平均行程時間最小為優化目標，包括候車時間和車內時間，如式（1）所示：

其中，T1表示無需換乘的乘客候車時間，當乘客均勻到達時，候車時間為候車乘客數與車頭時距的一半的乘積，如式（2）所示：

其中，T2表示需要換乘的乘客的候車時間，主要包括2 個部分，即第一次候車時間以及換乘候車時間，在第一次候車時，乘客為均勻到達，因此計算方式與無需換乘的乘客一致。 而在換乘候車時，乘客同時到達換乘站點，計算方式為換乘乘客數與車頭時距的乘積，如式（3）所示：

式（1）中，T（b）表示車內時間，計算方式為車輛從站點k －1 至站點k時，在車乘客數與站點k －1至站點k之間的車輛行程時間的乘積，如式（4）所示：

P表示研究時段內公交車運送乘客總數，即所有上車的乘客數，如式（5）所示：

式（1）～式（5）中，i為公交線路編號；j為公交班次編號；k為公交站點編號；K（tr）為換乘站點編號；β1，k為站點k無需換乘乘客占所有乘客的比例；β2，k為站點k需要換乘乘客占所有乘客的比例；bi，j，k為線路i班次j在站點k的上車乘客數；Hi，j，k為線路i在站點k班次j －1 與班次j的車頭時距；為線路i在換乘站點K（tr）班次j與最近的上一班換乘線路i′班次j′的車頭時距；Zi，j，k為線路i班次j到達站點k時的車廂總人數；Ti，j，k為線路i班次j到達站點k的時間，當k ＝0 時，Ti，j，0＝0。

目標函數計算的關鍵是確定公交運行過程中車輛和乘客狀態，即每個班次車輛到達各站點的時刻及駐站時間，其中駐站時間與站點上下車乘客數量相關。

1.1.1 公交車輛狀態的確認

對于非換乘站的車頭時距，即為同一線路中前一個班次j －1 與當前班次j到達站點的時間差，如式（6）所示：

而換乘站的車頭時距為線路i班次j與目標換乘線路i′班次j′的時間差，如式（7）所示：

其中，Ti，j，k為線路i班次j到達站點k的時間。

公交到達每個站點的時刻都可由其到達前一個站點的時刻遞推得到，即公交到達上一站的時間與在上一站的駐站時間以及在站點間的行程時間的加和，如式（8）所示：

其中，si，j，k－1為線路i班次j在站點k －1 的駐站時間；di，k為線路i中站點k與上一站k －1 的站間距單位為m；v為設計車速單位為m／s。 這里，公交站間行程時間由站間距離與設計車速的比值得到。

當k ＝1 時，公交車在站點1 的離站時刻由各線路第一班公交車的發車時刻與發車間隔的累加和組成，如式（9）所示：

其中，Fi，1為線路i第1 個班次的發車時間；hi，j為線路i班次j與班次j －1 的發車間隔。

公交在站點的駐站時間與上下車乘客數量有關，可由式（10）計算：

其中，bi，j，k為線路i班次j在站點k的上客數，單位為per；dpb為乘客平均上車時長，單位為s；ai，j，k為線路i班次j在站點k的下客數，單位為per；dpa為乘客平均下車時長，單位為s；ψ為車輛進站減速和出站加速所花費的時間，單位為s；αi，j為0－1變量；為線路i班次j在換乘站K（tr）與目標換乘線路i′班次j′的時間差，單位為s。

研究中，在換乘站時，對公交駐站時間進行控制，使得其可在站點等待目標換乘車輛到站。

1.1.2 乘客狀態的確定

公交車到達站點k時的車廂總人數為第1 站至第k －1 站所有站點上車人數與下車人數之差的累加和，如式（11）所示：

其中，bi，j，k為線路i班次j在站點k的上客數，單位為per；ai，j，k為線路i班次j在站點k的下客數，單位為per。

研究假設乘客到達率已知，且乘客是均勻到達的，對于從k站上車的乘客數量可由式（12）計算：

按先到先服務原則，將上車乘客的最晚到達時刻設為車輛到站時刻。 對于下車的乘客數量可由式（13）計算，即線路i班次j中從第1 站至第k －1 站所有到達站點k的乘客數：

式（12）～（13）中，λi，kk′為線路i從站點k至站點k′的乘客到達率；Hi，j，k為線路i在站點k班次j－1 與班次j的車頭時距。

1.2 約束條件

研究中考慮到車上其他乘客的出行時間，因此先到站車輛在換乘站等待目標線路車輛的時間不可超過3 min，如式（14）所示：

此外，由于公交運營成本和運營車輛數的限制，公交發車間隔也應受到最小間隔與最大間隔約束，如式（15）所示：

其中，hi，min為線路i的最小發車間隔；hi，max為線路i的最大發車間隔。

2 求解算法

2.1 優化思想

考慮到多線路不同發車間隔組合下，可滿足式（14）的班次j也不同，若單純地采用遺傳算法等經典啟發式算法進行運算，則在運算過程中極易生成不可行解，使得運算效率較低。 本研究從約束條件出發，設計分步優化算法，首先生成可行解集，再依據發車間隔組合的不同，將解集分成多個子集，運用鄰域搜索法對每個子集進行搜索，最后篩選出最優解。

算法的主要內容為，首先，在不同的發車間隔組合下，生成各自線路中滿足式（14）約束的班次j集合J（h1，h2）i，一個發車間隔組合下的所有可行解即構成一個子集；其次，采用實數編碼的方式，針對所有的發車間隔組合，從其對應的子集J（h1，h2）i中各自隨機選取一個可行解；隨后，以此可行解作為鄰域搜索的初始位置，并基于輪盤賭策略對相應的子集進行搜索；重復多次，直至滿足最大迭代要求，并篩選出最優解。

本研究所提出的算法具有以下特色：

（1）基于約束確定可行解集，避免生成初始解時，出現不可行解，提高初始解集的質量；

（2）在發車間隔組合不變的條件下，進行鄰域搜索操作，避免在搜索過程中對可行解結構進行重復判斷，提高搜索效率。

2.2 算法詳細過程

算法主要流程圖如圖1 所示。

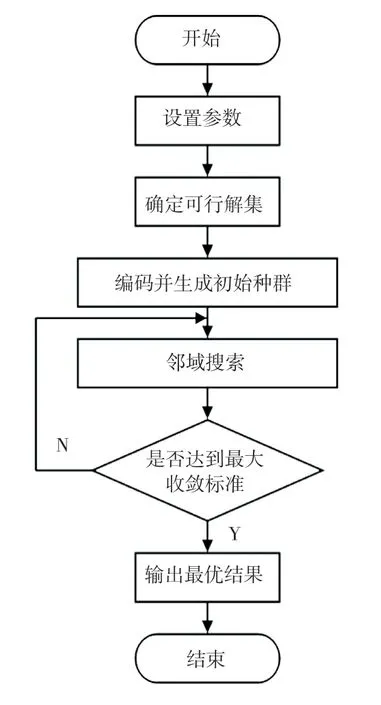
圖1 算法流程圖Fig. 1 Flowchart of the algorithm

Step 1設置參數。 設置種群數量、最大迭代次數、收斂標準等參數。

Step 2確定可行解集。 2 條不同的公交線路各取一個發車間隔(1，hi，max－ hi，min) ），組 成 發 車 間 隔 組 合，將輸入至模型中，計算2條線路中滿足式（14）約束的班次j，并加入各自的可行解集中，重復選擇多個發車間隔，生成各自對應的可行解集。

Step 3編碼并生成初始種群。 采用實數編碼的方式，且染色體由發車間隔與可控制班次組成，如圖2 所示。 改變發車間隔組合M次，每次均隨機生成一個初始可行解。

圖2 編碼方式Fig. 2 Encoding

Step 4鄰域搜索。 取目標函數值的倒數為適應度評價函數，保留每個子集中適應度函數值最高的解，并作為鄰域搜索時的初始位置，計算其鄰域所有解的適應度值與當前位置適應度值的差值，基于輪盤賭策略確定下一次迭代搜索方向。

Step 5重復以上操作，重復更新所有子集，直至滿足最大迭代要求或收斂標準。

3 案例分析

下文通過一個案例，將本文所提出的公交車輛駐站時間協同控制策略與無控制策略進行對比，驗證模型效益。 考慮2 條公交線路，線路1 單向設置13 個站點，線路2 單向設置15 個站點，2 條線路的換乘站點分別為線路1 的第5 站以及線路2 的第7站，如圖3 所示。 站點間距分別見表1、表2，研究時段取1 h，各站點乘客均勻到達，乘客OD 分布見表3、表4，其他參數設置見表5。

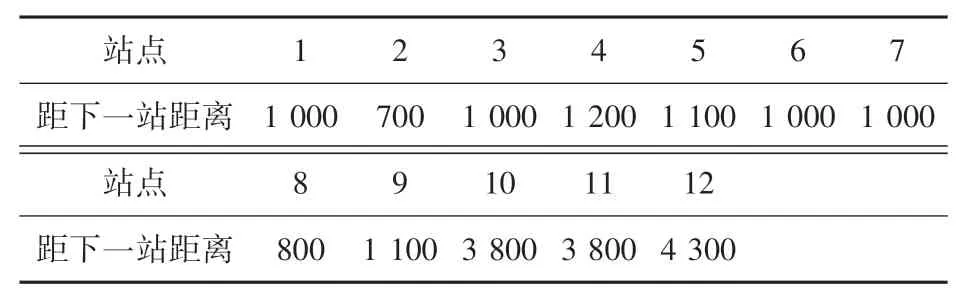
表1 線路1 站點間距Tab. 1 Distance between stations of line 1

表2 線路2 站點間距Tab. 2 Distance between stations of line 2

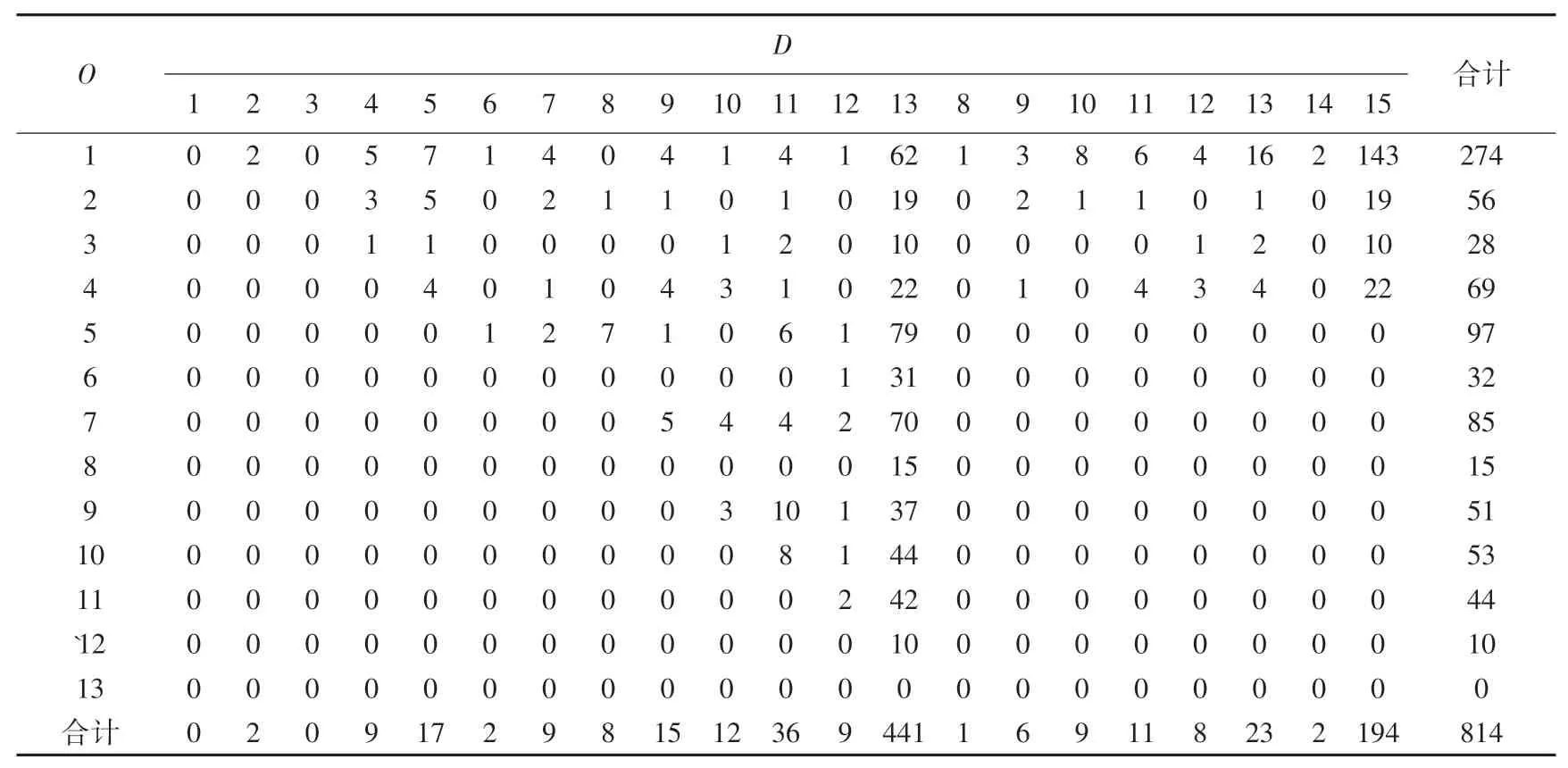
表3 線路1 乘客OD 分布矩陣Tab. 3 OD distribution of line 1

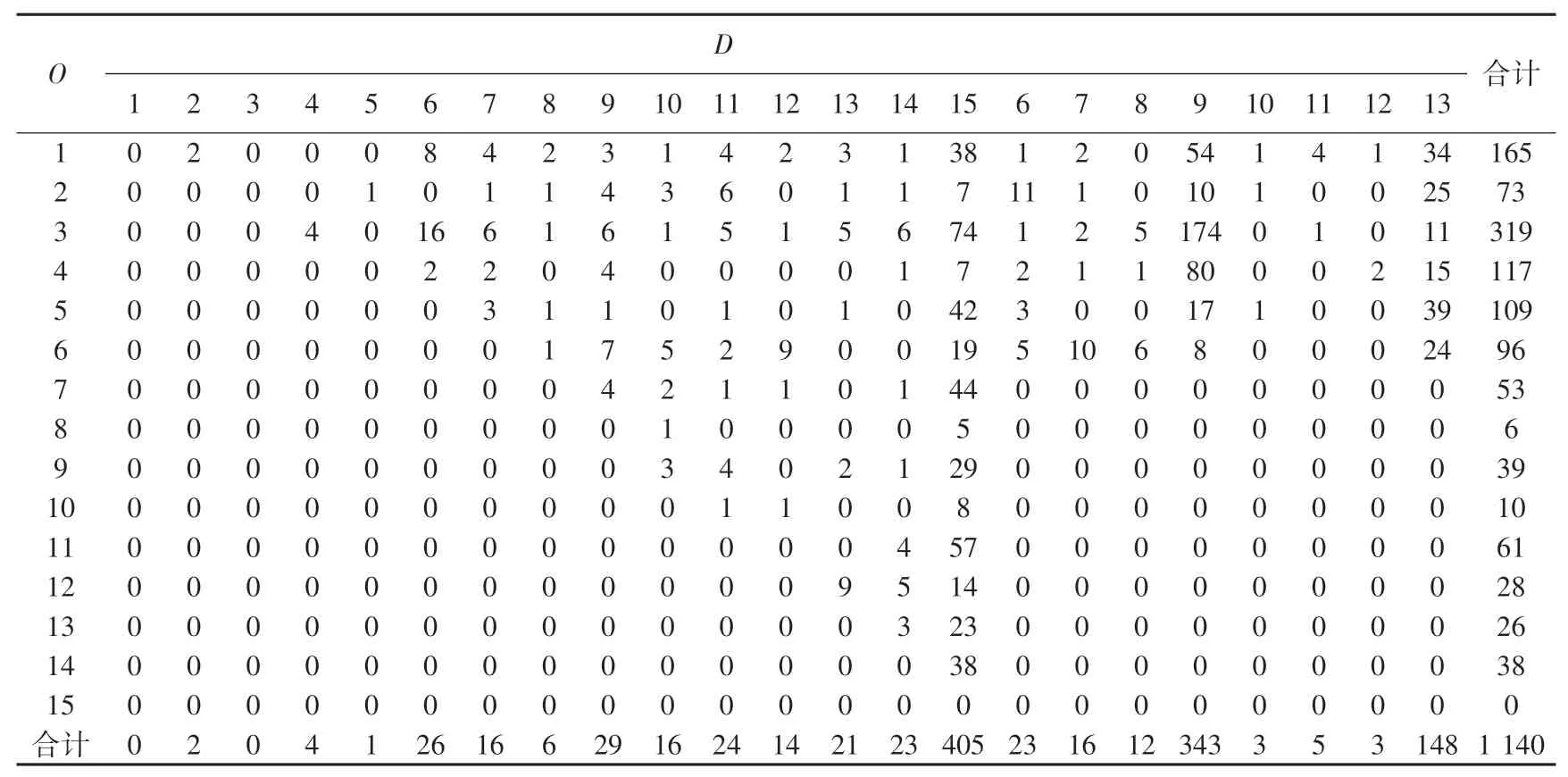
表4 線路2 乘客OD 分布矩陣Tab. 4 OD distribution of line 2

表5 參數設置表Tab. 5 Parameter setting table

圖3 公交站點位置圖Fig. 3 Bus stop location

運用本研究所提出的算法對模型進行計算，由于線路1 發車間隔為5～15 min，線路2 的發車間隔為8 ～15 min，故所有的發車間隔組合為88 種。 在Intel Core i3－12100 CPU （2.4 GHz）配置的個人計算機中，算法可以在2 min 內收斂，調度策略如圖4所示，計算結果見表6，最終平均乘客行程時間為21.26 min，在同發車間隔組合下，比常規調度策略減少乘客平均行程時間12.96%；在不同發車間隔組合下，比常規調度最優發車間隔減少乘客平均行程時間11.23%。

表6 結果對比表Tab. 6 Results comparison table

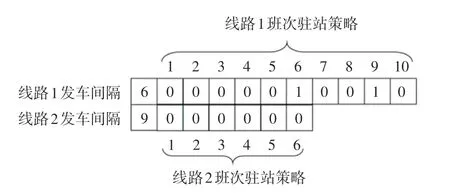
圖4 發車間隔及駐站時間控制策略Fig. 4 Control strategy for departure interval and dwell time

4 結束語

本文建立了多線路公交協調調度模型，并設計了一種優化算法，對公交車輛在換乘站點的駐站時間進行控制。 在多線路公交協調調度優化模型中，在已知乘客OD的條件下，對發車間隔以及車輛在換乘站點的駐站時間進行優化。 最終通過算例驗證了模型與優化算法的有效性。 通過分析，可以得出以下結論：

（1）本文所提出的多線路公交協調調度策略較常規策略可以減少乘客平均行程時間，提高公交服務水平。

（2）通過對發車間隔以及公交車輛在換乘站點的駐站時間進行優化，可以使得多線路乘客實現相互換乘，提高公交換乘效率。