基于模型預測電流控制的伺服電機系統轉矩脈動抑制研究

賴媛媛

(新鄉學院機電工程學院，河南新鄉 453000)

0 前言

永磁電機是伺服控制系統的核心部分，其性能好壞將直接決定整個系統的性能。在永磁電機中，由于實際的氣隙磁場分布非正弦，會導致反電動勢波形中也存在相應的諧波分量，從而引起額外的轉矩脈動，進而導致振動、噪聲，降低系統的控制精度。因此有必要采取一定的措施對其進行抑制。

國內外學者針對永磁電機轉矩脈動抑制方面的研究工作主要從電機本體和控制角度兩方面進行展開。在電機本體方面，主要通過降低齒槽轉矩、提高反電動勢波形正弦度來實現；而在控制方面則有改進控制算法、諧波注入等。

降低電機的齒槽轉矩主要是通過改變電機的設計參數以改變氣隙磁導分布或改變永磁體剩磁密度的空間分布，從而達到抑制齒槽轉矩的目的。具體有輔助槽、不等齒寬、不等槽寬、斜槽、優化槽口寬度[1-3]等。一般而言，雖然采用定子輔助槽能減小齒槽轉矩，但是由于齒部開槽，在一定程度上會降低電機的過載能力；不等槽寬和齒寬會引起額外的不平衡磁拉力；定子斜槽會大大增加工藝復雜度。此外，在優化反電動勢波形的正弦度方面，常用的方法包括磁極偏移、優化極弧系數、分段錯極、永磁體削角[4-7]等。其中，采用磁極偏移的方法雖然能夠有效減小齒槽轉矩，但是同時也會導致電機的不平衡磁拉力；永磁體削角的方法則會增加工藝復雜度，增加加工成本。

在控制方面，為了降低電機的轉矩脈動，通常采用改進控制算法或者諧波注入等。文獻[8]提出一種考慮定位力矩補償功能的模型預測轉矩控制方法，認為所提控制方法不但能實現定位力矩補償和轉矩脈動抑制，還具有較好的動態性能。文獻[9]則提出了一種模型預測直接轉矩控制方法，認為該方法與傳統直接轉矩控制相比，可以有效地抑制轉矩脈動，同時降低逆變器開關頻率，減小開關損耗。文獻[10-11]研究了永磁同步電機的模型預測電流控制，并對相應的預測進行了誤差分析及抑制。文獻[12]提出了一種基于特定次諧波注入法的諧波抑制方法，即在SPWM正弦信號中注入相應5次、7次諧波補償電壓，進而達到降低輸出電流特定次諧波含量的目的。

本文作者首先建立了適用于任意相永磁電機反電動勢諧波產生的脈動轉矩通用解析模型；然后，基于此模型，從控制的角度出發，提出采用電流諧波注入以補償反電動勢諧波引起的轉矩脈動控制策略，分析所需注入的電流諧波特性的一般表達式，并通過模型預測電流控制方法對電流進行控制。為驗證所提出方法的有效性，以一臺三相12槽10極表貼式永磁同步電機為例，通過MATLAB/Simulink設計了考慮反電動勢諧波的電機仿真模型，搭建了基于諧波注入的電機控制系統。此外，為進一步驗證所提方法的正確性，也進行了相應的試驗驗證。

1 12槽10極電機

1.1 電機結構

以一臺經典的12槽10極表貼式永磁電機為研究對象，電機的橫截面如圖1所示，同時其相應的關鍵設計參數列于表1。由圖1可見，在這種表貼式結構中，由于永磁體安放在氣隙中，使得交直軸磁路磁阻幾乎相等，因此，交直軸電感也幾乎相等，該類電機通常采用“id=0”的控制策略。

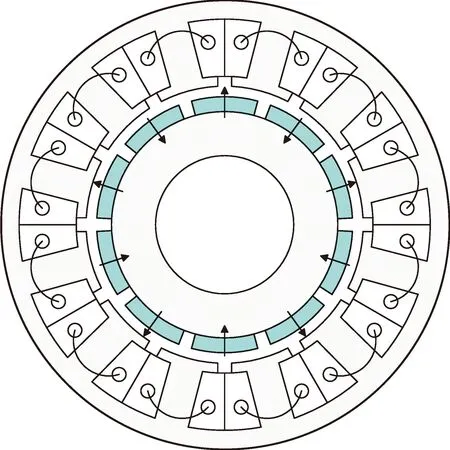
圖1 傳統12槽10極表面式永磁電機

表1 關鍵設計參數Tab.1 Key design parameters

1.2 反電動勢

一般而言，對于任意具有m相的永磁電機而言，其空載反電動勢的表達式為

(1)

式中：Ev為v次諧波幅值；ω為電角速度；t為時間；γv為相位，m為相數。

因此，通過有限元仿真計算得到圖1所示的3相12槽10極永磁電機的空載反電動勢仿真波形為圖2(a)所示，相應的諧波分析如圖2(b)所示。可以看到：該電機反電動勢波形中，除了基波之外，還有較大幅值的3次和5次諧波。其中3次諧波不產生轉矩脈動，而5次諧波則會引起轉矩脈動，因此，為提高系統的控制精度，有必要將其進行抑制。接下來將會詳細進行闡述。

圖2 反電動勢(a)及其諧波分析(b)

1.3 轉矩脈動產生機制

首先推導了適用于任意相電機反電動勢諧波引起的轉矩脈動的解析表達式；然后，基于此模型，分析所需注入的每相電流諧波特性。

通常，對于任意一臺m相永磁電機而言，其永磁轉矩可表示為

φμ],且|μ±v|=mk,k=0,1,2,…

(2)

因此，根據公式(2)，便很容易得到基波電流與v次反電動勢諧波作用產生的脈動轉矩，即公式(3)：

且|1±v|=mk,k=0,1,2,…

(3)

因此，如果采用注入μ次諧波電流以補償v次反電動勢諧波作用產生的脈動轉矩(忽略反電動勢高次諧波與μ次諧波電流之間的相互作用)，則有：

且|μ±1|=mk,k=0,1,2,…

(4)

此外，所注入的諧波電流也必須同時滿足以下條件：

(5)

因此，所需注入的諧波電流特性可由公式(5)求得，包括相應的幅值、諧波次數和相位。

2 數學模型

2.1 dq坐標系中的數學模型

在dq坐標系中，永磁電機的電流和磁鏈方程可分別由公式(6)和(7)進行表示：

(6)

(7)

式中：id、iq、ud、uq、Ld、Lq、ψd和ψq分別為直軸電流、交軸電流、直軸電壓、交軸電壓、直軸電感、交軸電感、直軸磁鏈和交軸磁鏈；Rs為定子電阻；ψpm為永磁磁鏈。

而電機的轉矩模型則可表示為

(8)

2.2 預測模型

首先，需要根據公式(9)對電機的數學模型進行離散化[11]，通常采用的方法是用一階差商代替一階導數，即：

(9)

式中：tk+1-tk為時間步長，可用h表示；k和k+1分別為第k次和第k+1次采樣。

將上式代入到式(6)—式(8)中，可分別得到：

(10)

(11)

(12)

3 基于諧波注入的控制系統仿真研究

3.1 控制系統原理

圖3為基于諧波注入的永磁電機模型預測電流控制原理框圖，包括電機模塊、電流預測模型、諧波電流注入模塊、模型預測控制器以及逆變器等模塊。以12槽10極永磁電機為例，電機的關鍵參數已在表1中給出。

圖3 控制系統原理Fig.3 Principle of control system

此外，根據圖2分析可知，該電機中5次諧波的幅值和相位分別是3.234.1V和161°，因此，再由式(5)可計算得到所需注入的諧波電流特性滿足以下公式：

(13)

3.2 仿真結果

圖4為基于MATLAB/Simulink仿真計算得到的注入諧波電流前、后的轉矩波形對比。可以看到：在注入諧波之前，系統的轉矩在5～7 N·m之間波動；而注入諧波之后，轉矩在5.5～6.8 N·m之間波動。顯然，注入諧波之后轉矩脈動被大大抑制，這與前面理論分析相符。

圖4 注入諧波前(a)、注入諧波后(b)轉矩波形對比Fig.4 Compare of torque waveforms before injecting harmonics (a)and after injecting harmonics(b)

圖5對比了注入諧波前、后系統轉速的波形。可以看到：與轉矩波形類似，當采用諧波注入時，轉速波形脈動也得到了明顯改善。

圖5 注入諧波前(a)、注入諧波后(b)轉速波形對比Fig.5 Compare of speed waveforms before injecting harmonics(a)and after injecting harmonics(b)

因此，總體而言，所提出的基于諧波注入的方法不僅可以改善系統的控制精度，同時也可以降低振動噪聲。

4 諧波注入控制系統試驗驗證

試驗是檢驗理論分析的重要方法[13-14]。為了進一步驗證上述所分析得到的控制方法的正確性，對一臺12槽10極三相表貼式永磁電機進行了相應的試驗研究。試驗的控制器采用dSPACE控制面板，它可以直接編譯Simulink 環境下的仿真模型，從而形成dSPACE試驗平臺可以辨識的代碼，最終建立起可在線調整各項參數的試驗系統，實現電機性能和控制方法試驗。試驗平臺如圖6所示。

圖6 試驗平臺Fig.6 Experimental platform

利用示波器，保存試驗過程中的電流和轉矩數據，如圖7所示。可以看到：注入諧波之后的電流波形發生了一定的畸變，使得其幅值有一定的增加，但是轉矩脈動確實也有一定程度的降低，這也與前面的分析相吻合。可見，所提出的方法有效。

圖7 電流(a)和轉矩(b)試驗測試波形Fig.7 Tested waveforms of current(a) and torque(b)

5 結束語

提出一種基于諧波注入的永磁電機模型預測電流控制方法。首先，建立了適用于任意相永磁電機反電動勢諧波產生的脈動轉矩通用解析模型；然后，基于此模型，從控制的角度出發，提出采用電流諧波注入以補償反電動勢諧波引起的轉矩脈動控制策略，分析所需注入的電流諧波特性的一般表達式，并通過模型預測電流控制方法對電流進行控制。為驗證所提出方法的有效性，以一臺三相12槽10極表貼式永磁同步電機為例，通過MATLAB/Simulink設計了考慮反電動勢諧波的電機仿真模型，搭建了基于諧波注入的電機控制系統。此外，為進一步驗證所提出的方法正確性，也進行相應的試驗驗證。研究結果表明：諧波注入前、后電機的轉矩脈動峰峰值從2 N·m降低到1.3 N·m。