振動臺正弦振動虛擬仿真技術研究

饒玉文，牛金皓

（1.南京晨光集團有限責任公司，南京 210000； 2.南京晨光集團有限責任公司，南京 210000）

引言

振動臺作為模擬振動環境，檢驗產品可靠性、動強度的一種有效手段，已經被廣泛應用于設計的驗證試驗中[1]。然而振動臺在實際應用中受到試驗設備和測點數量的限制不能全面獲得試驗件各個部分的響應特性[2]，因此在有些情況下不能僅僅以振動臺試驗結果作為結構、產品設計的唯一依據。虛擬振動仿真技術利用計算機技術的優勢彌補了振動試驗存在的缺陷，通過虛擬仿真不僅可以預示振動響應，還可以對產品試驗不便測試的部位進行模擬測試[3]，指導試驗開展和結構與方案設計。

電動振動臺主要由活動系統（驅動線圈和工作臺）、磁路系統、彈性支撐系統、導向系統及冷卻裝置等組成，其中導向機構限制振動臺的橫向運動，彈性支撐系統產生恢復力和支撐力[4]，活動系統是指在帶有工作臺面的骨架上繞制激勵線圈，并用環氧樹脂將兩者固封在一起的組合件，通常稱為動圈，動圈是活動系統的關鍵部件，是振動臺的核心部分[5]。振動試驗仿真最關鍵的技術是建立正確的系統分析模型[6]，因此可以獲取準確的動圈模型后，施加對應真實狀態下的邊界條件和激振力便可模擬振動臺的虛擬振動仿真。

本文以8 t電動振動臺為對象，通過模態試驗對動圈實物模型進行修正，利用ANSYS軟件進行兩次頻響計算，最終求出正弦振動條件下臺面兩點平均控制的響應。

1 振動臺結構模型建立

1.1 動圈結構建模

動圈是主要由骨架、線圈、工作臺面和臺面螺釘等部分組成，其中骨架部分含側板和8片環形立板，結構示意圖如圖1所示。其中螺釘為不銹鋼材料，骨架為鋁合金材料，線圈部分比較復雜，本文振動臺為水冷式振動臺，驅動線圈由鎂鋁合金薄環、水管、銅制線圈以及環氧樹脂組合而成，建模時將線圈視為實體結構。

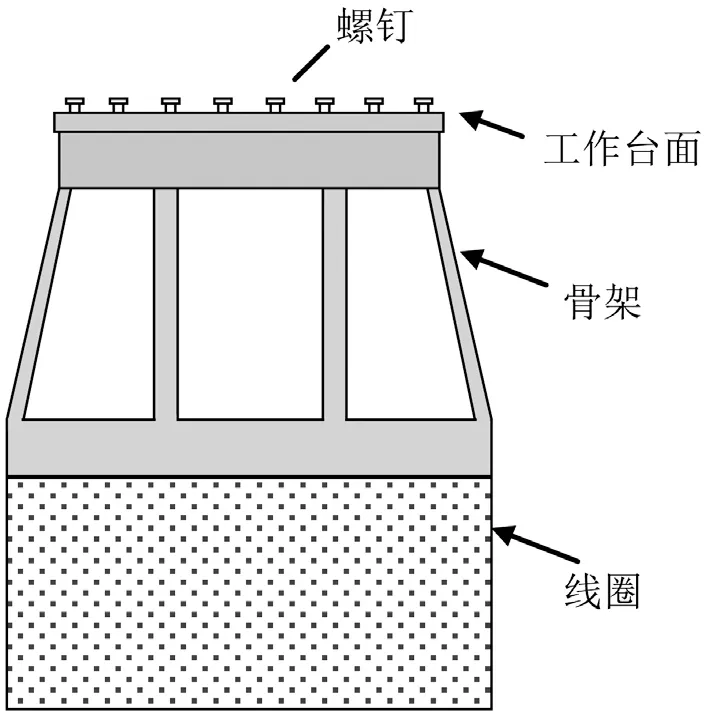
圖1 動圈結構示意圖

1.2 動圈模型修正

有限元是基于材料屬性（楊氏模量、泊松比、質量密度等）和要模擬系統的物理尺寸進行求解的[7]。為建立更加準確的數學模型，需要對模型進行修正處理，動圈模型修正的主要原則是修正各部分結構的彈性模量、密度和質量，同時保證數值計算的固有頻率和振型與模態試驗的結果一致。模態試驗數據是仿真模型修改的主要依據，修正結果的優劣將直接影響仿真的精度，其中動圈骨架和臺面螺釘均可在材料參數手冊中參數值附近進行查找調整，驅動線圈組成較為復雜，只能通過不斷調整參數以達到與試驗數據相近的結果。

1.2.1 動圈模態試驗

自由模態反映的是試件固有的振動特性，最能反映結構的自身特點[8]。采用橡皮繩懸掛動圈模擬自由邊界，以反映動圈的真實固有特性。根據動圈結構特點共布置88個三向測點，分別分布在動圈臺面、骨架和線圈上，試驗狀態與模態測點布置如圖2所示，使用多參考點移動傳感器法進行力錘敲擊模態試驗。

圖2 模態試驗

1.2.2 模型修正

根據模型修正原則和模態試驗結果，不斷調整材料參數，適當修正模型邊緣結構，最終動圈各個部分材料參數值確定如下：骨架密度為2 800 kg/m3，彈性模量為69 GPa；線圈密度3 000 kg/m3，彈性模量72.3 GPa。動圈重量為52.37 kg，實際重量為50.8 kg，誤差為2.9 %。模態頻率與振型結果如表1所示。

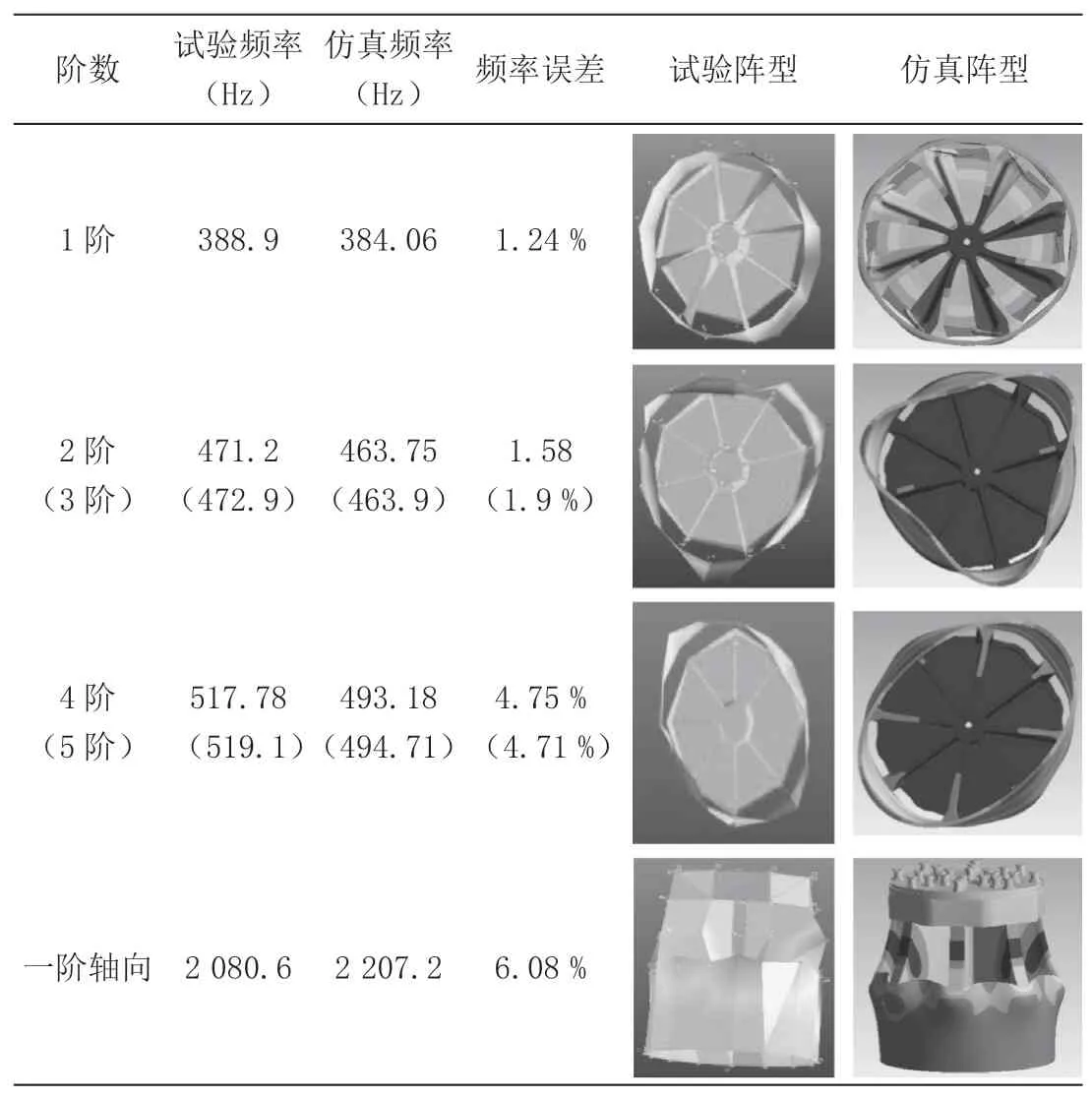
表1 試驗與計算模態結果對比

根據模態結果與振型圖可以看出，動圈一階模態388.9 Hz，表現為肋板扭轉。二階與三階、四階與五階均為對稱模態，表現為線圈的呼吸擴張運動，前五階誤差均在5 %以內。其中一階軸向共振頻率影響動圈軸向伸縮運動并決定了振動臺臺工作頻率的上限范圍[9]，模態試驗得到軸向一階頻率為2 080.6 Hz，修正后動圈的一階軸向頻率為2 207.2 Hz，誤差為6.08 %，修正得到的動圈模型能夠反映動圈的基本特征。

2 正弦振動仿真分析

2.1 激勵施加分析

電動振動臺的基本工作原理與擴音器原理類似，是基于載流導體在磁場中受到電磁力作用而運動。振動臺臺體中的勵磁線圈產生恒定磁場，信號發生器產生交變信號，經過功率放大器后，輸入到動圈，電磁力會在驅動線圈的繞組下產生，使得臺面產生向上和向下的往復運動，電磁力 F = BIL[10]。其中 B 為恒定磁場中的磁感應強度（Wb/m2），L 為動圈繞線的有效長度（m），I 為動圈中的電流（A）。

臺面在激振力F的作用下振動，振動幅值取決于電流I，對于給定的振動臺，電流與電壓成正比，因此可用力F來代替驅動電壓進行激勵，線性假設條件下，控制點響應A（f）、驅動線圈中的驅動力幅值F（f）、頻響函數值H（f）存在以下關系：

以兩點平均控制為例，需進行兩次頻響計算，先施加一定的激振力譜F1（f），獲取臺面控制點1和控制點2的響應B1（f）和B2（f），這兩點的平均響應為：

此時由式（1）求出頻響函數值H（f）=B（f）/F1（f），若實際振動給出的正弦振動條件為則新的激振力譜為：

2.2 正弦掃頻仿真

振動臺動圈通過工作臺面的U型懸掛彈簧懸掛在振動臺剛性臺體上，懸掛彈簧均勻分布在工作臺面下方的四周邊緣，構成彈性支撐系統提供恢復力和支撐力，限制動圈旋轉和擺動的作用，在ANSYS中約束彈簧連接部位節點，僅保留軸向自由度，動圈中央剛性軸限制動圈不必要的橫向運動，在ANSYS中采用彈簧單元約束剛性軸底部，僅保留垂向平動自由度。以動圈臺面兩點平均控制為例，進行2 g狀態下的正弦掃描振動，響應計算范圍為（5～2 000）Hz，模態計算范圍為（0～3 000）Hz。

在動圈驅動線圈表面任意施加600 N的激振力，進行第一次頻響計算，計算得到臺面控制點1與控制點2的加速度響應，如圖3（a）所示，整體趨勢與圖3（b）電動振動臺典型恒流幅頻特性曲線一致，第一個諧振頻率是由振動臺的懸掛支承系統諧振而引起的，稱為懸掛系統自振頻率，第二個諧振峰是由于振動臺動圈諧振引起的，為動圈第一軸向共振頻率。

圖3 幅頻特性

根據得到的臺面兩點加速度響應的平均值和公式（3），可求出最終施加在驅動線圈上的激振力譜。經過力譜輸入仿真計算，便可得到動圈臺面兩點加速度平均響應結果。

2.3 正弦掃頻試驗

圖4為8 t振動臺正弦掃頻試驗，點1和點2為振動控制點，點3、4為振動監測點，對臺面進行頻率范圍（5～2 000）Hz的2 g加速度正弦掃頻振動，控制方式為兩點平均控制，試驗粘貼測點位置與有限元模型測點位置盡量保持一致，將兩點平均控制響應譜的試驗結果與仿真結果進行對比，見圖5，在（5～2 000）內的試驗與仿真的加速度響應結果較為吻合，仿真的加速度值在2 g上下浮動，變化較小，可以看出仿真的精度較高。在1 700 Hz之前兩者結果十分接近，1 700 Hz之后，試驗結果出現一定波動性。

圖4 掃頻試驗

圖5 兩點平均控制響應譜結果對比

從圖6和圖7中可以看出，臺面監測點3與監測點4的仿真結果曲線都較為平穩，而監測點的實驗結果均在1 200 Hz后出現波動，這主要是因為振動臺實際結構復雜，存在運動部件在高頻段自身會發生彈性變形及局部振型等因素，虛擬仿真則有效避免了不均勻性的影響。

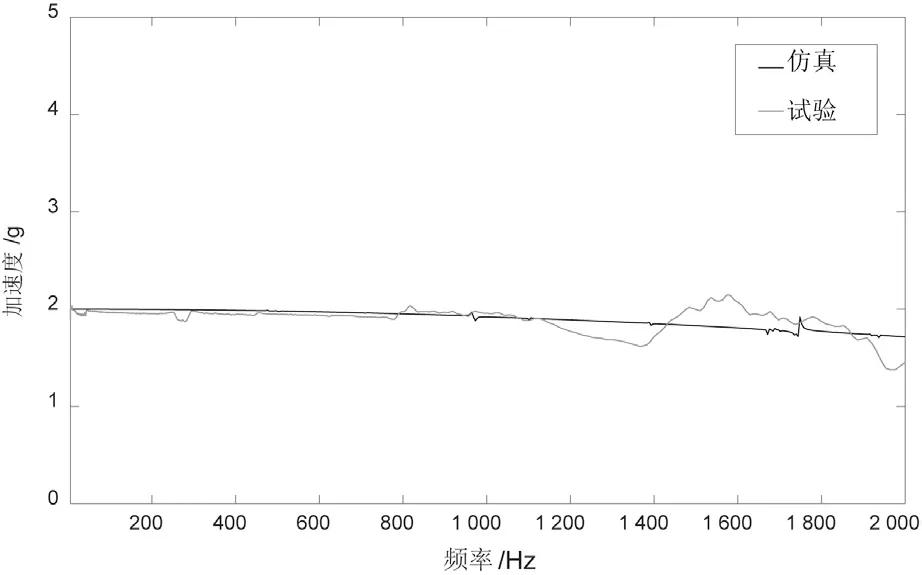
圖7 監測點4加速度響應

4 結論

本文根據動圈實際結構與模型試驗數據對動圈進行模型修正，修正各部分結構參數后使得模型有限元得到的前五階固有頻率與模態試驗結果一致，誤差在5 %以內，一階軸向固有頻率的仿真與試驗結果較為接近，同時保證了質量和振型的一致性，建立了能夠反映8 t電動振動臺動圈特性的動圈有限元模型，根據動圈實際安裝狀態施加相應的邊界條件，基于振動臺工作原理，進行頻響計算反推出2 g加速度正弦振動條件下施加在驅動線圈上的激振力譜，以該激振力譜為條件進行正弦掃頻虛擬仿真，與實際掃頻試驗結果進行了對比，臺面兩個控制點得到的平均加速度響應值的仿真與試驗結果較為吻合，虛擬仿真掃頻能夠較好的模擬出正弦振動試驗結果。由于振動臺結構本身的非線性等因素，正弦掃頻試驗部分監測點在高頻段會出現局部的波動，而仿真在線性假設條件下避免了這些因素，仿真結果均很平穩，精度較高，但兩者結果的整體趨勢仍然一致，正弦振動虛擬仿真可以對掃頻振動進行較好的預測。