合成射流對層流狀態下圓柱輻射噪聲的影響*

宋健 任峰 胡海豹 陳效鵬

(西北工業大學航海學院,西安 710072)

主動流動控制是降低流動噪聲的新型途徑,近年來吸引了研究者的廣泛關注.利用二維格林函數,推導得到了忽略四極子影響的聲比擬方程的二維時域解.在此基礎之上,基于格子Boltzmann 方法為核心的流場求解器以及聲比擬方程為核心的聲場求解器,在低雷諾數(Re=100)下,開展了合成射流頻率和相位差對圓柱繞流近壁流場和聲輻射遠場影響的數值模擬研究.結果表明,在利用合成射流減小圓柱阻力時,出現了兩種頻率鎖定狀態,且遠場輻射噪聲會發生明顯變化.提高射流頻率或減小相位差會增強射流的自噪聲,導致遠場輻射聲壓進一步增大,并使得指向性由偶極子類型轉變為單極子類型.在各個控制參數組合下,遠場的總輻射噪聲增加,與未施加控制時相比聲功率增加了4 到18 dB,同時,阻力方向的噪聲始終增強.本研究可為探索低輻射噪聲的合成射流控制策略提供參考數據.

1 引言

鈍體繞流是生活中常見的流動形式之一,流體從鈍體表面分離、失穩產生非定常的渦脫落,并向外輻射噪聲[1].鈍體繞流輻射噪聲是典型的流-固-聲耦合問題,廣泛存在于工程應用之中,如飛機起落架,潛艇圍殼以及高速列車等方面.Inoue 和Hatakeyama[1]將圓柱繞流發聲機理解釋為: 當尾渦從圓柱表面脫落時,會誘導產生沿表面外法線方向的壓力脈沖,并以偶極子類型向外輻射噪聲.鐘思陽和黃迅[2]以平板前緣和后緣為例,解釋了結構表面脈動壓力輻射噪聲的機理.上述研究表明尾渦脫落對圓柱輻射噪聲具有重要影響.因此可以通過控制尾渦脫落來改變圓柱的流體動力,從而調制輻射噪聲.

主動流動控制通過對流場施加小擾動來調制流動結構,在增升[3]、減阻[4]和抑振[5]等方面取得了顯著效果.王成磊等研究了前吸后吹控制對渦激振動圓柱[5]、合成射流控制對渦激振動圓柱[6,7]以及合成射流控制對固定圓柱[8]流場的影響.通過數值模擬證明了對固定圓柱施加開環合成射流控制后,存在頻率鎖定的情況,并結合線性穩定性分析,確定了發生頻率鎖定的控制參數的理論變化范圍[8].除此以外,利用深度強化學習還能實現更為復雜的控制目標[4,9,10].主動流動控制對流場的影響已經成為近些年來研究的熱點,而主動流動控制對聲場的影響也吸引了流致噪聲領域研究者的不斷關注[11-21].Du 和Sun[11]利用閉環旋轉控制,從渦和聲兩個角度出發,得到了展向渦量與升力系數及聲壓之間的線性關系,實現了最大10 dB 的降噪效果.黃迅等[12]在圓柱表面設置等離子射流裝置,在雷諾數為2.1×105條件下將遠場范圍的噪聲降低了3 dB.Ma 等[13,14]研究了強迫振動控制對圓柱噪聲輻射的影響,將控制頻率對聲壓的影響規律分為三種情況,并給出了相應的經驗公式.Guo[15]認為流固耦合是非線性的過程,但聲傳播是線性的,基于聲場的線性疊加原理,提出了一種利用相位相消實現低噪聲輻射的射流控制方法.

在圓柱上施加合成射流控制時,射流孔處周期性的瞬時質量變化相當于在流場中引入了單極子聲源[16],同時由于射流孔處的動量也在周期性變化,還會在圓柱表面產生偶極子聲源.Inoue 等[16]利用強度較小的吹/吸控制進行研究,施加控制之后圓柱流場幾乎不發生變化,也避免了頻率鎖定情況的出現.結合數值模擬的結果并從聲源線性疊加的角度出發,解釋了吹/吸控制產生的單極子和圓柱表面流體動力脈動產生的偶極子之間相互作用對聲場的影響機理.但在減阻過程中,合成射流控制不僅會引入額外的噪聲,還會對圓柱尾渦脫落產生影響,造成圓柱表面流體動力的變化,導致流體動力產生的偶極子發生改變,并最終改變遠場的輻射噪聲.因此,需要進一步研究不同頻率和相位差的合成射流控制對圓柱繞流聲場的影響.

數值模擬是研究流噪聲的有效途徑.根據是否需要求解聲比擬方程,可以將流噪聲數值模擬方法分為直接方法和混合方法[22].直接方法是通過求解可壓縮流動控制方程組獲得流場中的壓力.混合方法則是將流場與聲場解耦,將流場計算結果作為輸入求解聲場.三維情況下,聲波以脈沖形式向空間中傳播,通過直接方法與混合方法求解得到的聲場符合良好.但在研究二維問題時,除了聲源發出的聲壓脈沖之外還包含尾波[23],需要將之前時刻的影響全部疊加起來,在三維條件下推導的聲比擬方程的解不再適用.Guo[23]通過更換格林函數,獲得了Ffowcs Williams/Hawkings 方程的二維頻域解.類似地,Inoue 和Hatakeyama[1]得到了考慮偶極子作用的Curle 方程的時域解,但考慮單極子聲源的聲比擬方程的二維時域解未見報道.

因此,本文首先推導了計及單極子和偶極子作用的聲比擬方程的二維時域解.隨后基于格子Boltzmann 方法和浸沒邊界方法獲得的流體動力信息,利用混合方法求解聲場.本文主要研究了合成射流控制的頻率和相位差對圓柱流體動力和輻射噪聲的影響,厘清了合成射流控制對聲場的影響規律和作用機理,以期為探索低輻射噪聲控制策略提供參考數據.

2 物理模型

本文針對外部流場為均勻流場,雷諾數Re=100 的二維固定圓柱繞流問題進行研究,此時圓柱下游會形成非定常、周期性脫落的尾渦.為了施加合成射流控制,將一對大小相同的射流孔關于水平軸線對稱地排布在下游分離點附近位置.射流孔分別周期性地向流場中施加擾動,調制壁面附近流場結構,并改變近遠場的聲輻射特性.

如圖1 為合成射流裝置的示意圖,流體沿x軸正方向流動,其中U0為外部流場速度,D0為圓柱直徑,參數的選取與研究合成射流對流場影響的設置[6]保持一致.射流孔大小為d=πD0/72.射流孔中心位置與圓心連線與x軸的夾角為±γj,選定為γj=70°,即分離點附近,施加的開環控制律為

圖1 基于合成射流的圓柱主動控制示意圖Fig.1.Schematic of the active control of a circular cylinder using synthetic jets.

其中usj為射流的瞬時速度,上標u 和l 分別代表上下射流孔,ujet為射流速度大小.fsj為射流頻率,?為相位,并定義相位差為Δ?=?u—?l.

由于圓柱輻射噪聲以升力偶極子占主導,因此射流方向與外流方向相同,避免直接干擾升力變化.射流強度與射流速度有關,可用動量系數Cμ表示,其定義為

發生頻率鎖定時,渦脫落頻率始終保持在射流頻率的整數倍或整數分之一倍,如1/2 倍或1/3倍.此時流場結構比較簡單,特征頻率較少,且能夠實現鈍體平均升力增大、平均阻力減小以及流動分離受抑制等.因此本文在頻率鎖定情況下研究射流控制對圓柱繞流輻射噪聲的影響.考慮到射流速度過小將難以發生頻率鎖定[7],因此將射流速度設置為ujet=2U0,此時Cμ=0.239.

采取不施加控制時的渦脫落頻率fn對計算得到的頻率f進行無量綱

以x方向為升力方向,y方向為阻力方向,升力系數CL、阻力系數CD以及斯特勞哈爾數St由如下公式計算,

其中FL和FD分別為圓柱的升力和阻力;ρ0為流體密度,取為1.

本文選取的控制參數組合如表1.

表1 主動控制的參數范圍Table 1.Parameter range of the synthetic jet based active control.

3 數值方法

3.1 流場計算方法

本文基于格子Boltzmann 方法求解流場,并利用浸沒邊界方法計算流體和固體間的相互作用.通過D2 Q9 格式對He-Luo 模型[24]進行離散,并采用多松弛時間格式[25]提高計算的穩定性.以MRT 形式的方程作為控制方程:

其中g為分布函數;x為格點位置;δt為格子時間;e為離散速度.對于D2Q9 模型,下標i∈ [0,8].轉換矩陣M為

Λg為松弛系數矩陣,Λg=diag(s0,s1,···,s8)[25],其中s7,s8與黏性相關.為采用Guo 和Zheng[26]提出外力源項,可表示為

其中F=[Fx,Fy]為使用浸沒邊界方法計算得到的圓柱表面Lagrange 點對流體格點的作用力.宏觀速度u和壓強p求解為

m為矩空間的分布函數,取格子聲速cs為3—1/2c,c為格子速度,則矩空間的平衡態分布函數meq可表示為

浸沒邊界方法是將固體對流體的作用表示為體積力代入流場進行計算.通過沿圓柱表面排布一系列Lagrange 點來表示曲面邊界,無需生成貼體網格,保持了流體網格的正交性,提高了計算效率.浸沒邊界方法的核心在于通過修正速度來使得流體網格和對應位置Lagrange 點的無滑移和無穿透條件得以滿足.利用修正速度可以獲得圓柱表面Lagrange 點受到的流體作用力和以外力源項模型(7)施加的流體格點受到的體積力.本文利用四點形式的狄拉克函數[27]在流體網格與對應Lagrange點之間進行插值獲得修正速度,采用多重直接力法[28]對浸沒邊界力進行求解.

流場數值模擬的設置如下圖2,計算域大小為60D0×20D0,圓柱放置在距離左端入口20D0,距離上壁面10D0的位置.流體以速度U0從左向右勻速流過,入口設置為速度入口,出口設置為壓力出口,均通過非平衡態外推格式實現[29],上下壁面為半步長反彈格式[30]實現的自由滑移邊界條件.

圖2 計算域示意圖Fig.2.Schematic of the computational domain.

3.2 聲場計算方法

二維計算時需要疊加之前時刻的影響,Inoue等[1]采用格林函數(7)獲得了Curle 方程的二維時域解,格林函數的具體形式為

其中H為Heaviside 函數

其中cs為聲速;z,y分別表示接收點和聲源的位置.t'為時間積分變量,表達式為t'=τ'+τ,其中τ為延遲時間,采用τ=t— |z—y|/cs計算,τ'用來表示之前時刻的作用.令r為接收點到聲源的距離,表示為r=z—y,對于緊致聲源來說滿足r ≈ z.

考慮到射流控制具有單極子聲源的性質,本文主要參考Inoue 和Hatakeyama[1]的研究推導聲比擬方程的二維時域解.根據Goldstein 給出的積分形式[31]的聲波方程:

其中ρ0為流體密度;soild 為壁面,fi為壁面受到的各個方向的外力;un為垂直于壁面的法向速度;l為壁面的單位長度.Tij為四極子聲源,在低馬赫數條件下可以忽略.交換積分和微分次序,可得

T代表足夠長的時間范圍內,聲源區對接收點聲壓仍有影響,因此用無窮遠的時間代替,并利用Heaviside 函數性質可將(13)式化簡為

將空間導數轉化為時間導數,并用τ=t— |r|cs以及t'=τ'+τ整理待積分項分母.舍去τ′2項[1],得到了聲比擬方程的二維時域解,

3.3 數值模擬方法驗證

時空分辨率由馬赫數Ma確定,設置為Ma=U0/cs=0.1.T0=D0/U0表示計算中的特征時間.Lagrange點數量隨Euler 網格分辨率線性變化,使得相鄰Lagrange 點之間的距離接近Euler 網格尺寸.網格無關性檢驗的結果如表2.從表2 中可以看出在D0=64Δx的中等空間分辨率的網格下,繼續加密網格,升力系數CL和斯特勞哈爾數St的變化較小.因此,本文選取該空間分辨率的網格對流場進行求解.流場求解在格子單位體系下進行,空間步長為δx,時間步長為δt.實際的空間步長和時間步長可以通過特征長度D0和特征時間T0進行換算.計算問題與實際問題的一致性則是通過相似準則來保證,而本文需要滿足雷諾數Re和馬赫數Ma相同.首先通過馬赫數Ma確定速度U0,通過網格無關性驗證獲得特征長度并計算特征時間,最后通過雷諾數Re=(ρ0U0D0)/μ計算得到黏性.

表2 網格無關性檢驗Table 2.Validation of the mesh resolution and verification at Re=100.

流場計算完成之后提取出固體表面速度和流體動力信息,求解方程(8)得到接收點聲壓.聲場求解同樣在格子單位下進行,時間步長與流場求解的時間步長保持一致,而聲場計算只用到單個接受點的時間信息,因此計算結果的準確性與空間分辨率無關.將圓柱圓心放置在計算域中心,并作為坐標原點(0,0),采用混合方法在140D0×140D0范圍計算得到不施加控制時的圓柱聲輻射場如圖3,此時升力偶極子占主導.

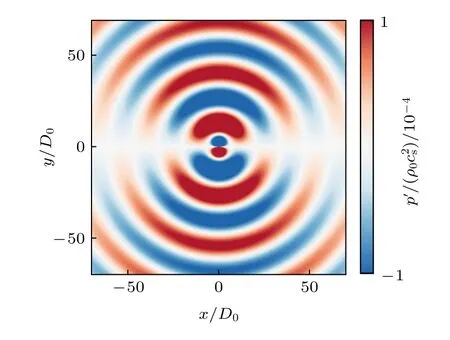
圖3 利用流-聲混合方法求解得到的瞬時聲輻射場Fig.3.Instantaneous pressure field computed via the hybrid flow-acoustics solver.

在此基礎之上,進一步地驗證推導得到的解的準確性.對圓柱施加射流頻率為2 的同相位合成射流控制,分別利用LBM 進行直接模擬、二維Curle方程時域解[1]以及本文使用的(8)式進行混合模擬,其中直接模擬的松弛時間及吸收層設置參考文獻[34].(70D0,0)處的聲壓瞬時變化曲線如圖4.三種方法計算得到的聲壓頻率基本相同,由于沒有考慮單極子的作用,求解Curle 方程二維時域解的結果與直接模擬的結果相比有顯著差別,而修改后的二維時域解(8)式與直接模擬結果的一致性良好.

圖4 測點(70D0,0)位置瞬時聲壓對比圖Fig.4.Comparisons of temporally varying sound pressure at monitor point (70D0,0).

4 結果與討論

4.1 射流控制對圓柱近壁流場的影響

圓柱輻射噪聲與流體動力變化相關,而合成射流控制通過向圓柱分離點附近注入擾動能夠有效改變流場結構,因此在研究合成射流對遠場輻射噪聲的影響之前首先研究其對圓柱繞流近壁流場的影響.

在本文所考慮的工況下,不施加控制時,尾渦以固定頻率fn脫落,且渦脫落頻率fn與雷諾數存在對應關系[35].施加控制后,應當存在兩個主要頻率即射流頻率fsj和尾渦脫落頻率fn,同時由于非線性的影響,還會產生和頻fsj+fn、差頻fsj—fn以及各種諧頻,此時流場處于調制階段.流場進一步發展,可能導致頻率鎖定狀態,此時擾動被放大,在一定射流頻率變化范圍內,尾渦脫落被射流“捕獲”,表現為尾渦以射流頻率周期性地脫落,此時流場中只存在射流頻率及其諧頻.若未發生頻率鎖定,流場始終處于調制階段,升力脈動曲線按照放大-縮小-放大的趨勢變化,尾渦不以明顯的周期脫落.根據控制頻率和渦脫落頻率的倍數關系,可以將頻率鎖定參數變化范圍分為三個基本區域[8]: 當渦脫落頻率與控制頻率接近,為基本鎖頻(primary lock-on);當渦脫落頻率為控制頻率的整數分之一倍時,為次調和鎖頻(subharmonic lock-on);當渦脫落頻率為控制頻率的整數倍時,為上調和鎖頻(superharmonic lock-on).根據頻率鎖定時渦脫落頻率與射流頻率的倍數關系,如1/2 倍或1/3 倍,可將次調和鎖頻進一步分為第二鎖頻(secondary lock-on)和第三鎖頻(tertiary lock-on).在本文選取的控制參數中,僅出現了基本鎖頻和第二鎖頻,如圖5,紅色正方形標記點為發生頻率鎖定的參數組合,黑色叉號標記點為沒有發生頻率鎖定的參數組合.因此本文主要在這兩種情況下討論合成射流控制對輻射噪聲的影響.從圖5 中可以發現,基本鎖頻區包含的參數組合更多,說明基本鎖頻是一種更常見的受控狀態.

圖5 不同控制參數下發生頻率鎖定的情況Fig.5.Lock-on events under a range of control parameters.

頻率鎖定發生時,剪切層在射流擾動的非線性作用下,以射流的頻率脫落.圖6 對應升力由正到負時刻的流場渦量云圖,其中虛線是渦邊界,由λci=0.2[36]渦判據計算得到.圖6(a)為未施加控制的狀態,圖6(b)和圖6(d)為發生頻率鎖定的狀態,圖6(c)為未發生頻率鎖定的狀態.其中,由于圖6(b)的控制頻率為=1,因此渦脫落頻率沒有發生變化,流場云圖與圖6(a)沒有顯著差別,而圖6(d)的控制頻率為=2.1,計算域內的渦對數量增加,表明渦脫落頻率增加.同時圖6(c)為未發生頻率鎖定狀態,圖6(c)的尾渦向上偏移,不再保持空間對稱分布狀態.

圖6 典型控制參數下流場云圖 (a) 未施加控制時;(b) =1,Δ?=π;(c) =2,Δ?=π;(d) =2.1,Δ?=0.5πFig.6.Instantaneous vorticity contours: (a) Unforced case;(b) =1,Δ?=π;(c) =2,Δ?=π;(d) =2.1,Δ?=0.5π.

圖7 為CL-CD相圖,從圖中可以發現,未施加控制時,相圖為“8”字形曲線,這是由于阻力脈動頻率為升力的1/2.發生頻率鎖定時,圖中僅包含一條清晰閉合的曲線.而未發生頻率鎖定時,CL-CD曲線隨時間變化,包含多種頻率,因此CL-CD相圖明顯失序.

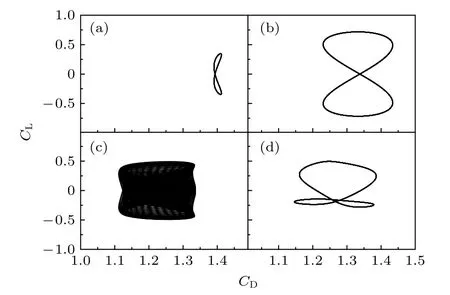
圖7 CL-CD 相圖 (a)未施加控制時;(b) =1,Δ?=π;(c) =2,Δ?=π;(d) =2.1,Δ?=0.5πFig.7.Phase diagrams of CL-CD: (a) Unforced case;(b) =1,Δ?=π;(c) =2,Δ?=π;(d) =2.1,Δ?=0.5π.

進一步地,提取出圓柱表面流體動力變化,如圖8.其中第三列為利用快速傅里葉變換(FFT)對包含30 個周期以上的流體動力信息進行統計的結果.未施加控制時,如圖8(a),升力隨尾渦脫落而周期性地變化,在頻譜中也表現為以渦脫落頻率為主.而施加控制后,阻力脈動增加.如圖8(b),施加=1,Δ?=π 條件下,升力和阻力的脈動頻率沒有發生變化,但脈動幅值顯著增加.而在圖8(d)中=2.1,Δ?=0.5π,由于頻率鎖定的發生,升力脈動頻率偏離了自然渦脫落頻率,出現了1/2 倍射流頻率的分量,同時其升力脈動減小,阻力脈動增加.而如圖8(c),未發生頻率鎖定時,由于存在f*=0.97 和=2 兩個沒有倍數關系的頻率,瞬時升阻力曲線沒有明顯的周期.

發生頻率鎖定時流場中的頻率存在倍數關系,所以CL-CD相圖是一條清晰閉合的曲線,但其對稱性會隨控制參數發生改變.圖8(b)是上下射流的相位差為Δ?=π,每一時刻射流的總動量注入為0,圓柱的升阻力變化均來自于尾渦脫落,因此CL-CD相圖保持了良好的對稱性,與此形成對比的是圖8(d)中相位差為Δ?=0.5π,射流注入的動量額外增加了圓柱表面流體動力的變化,導致CL-CD相圖不再保持對稱.

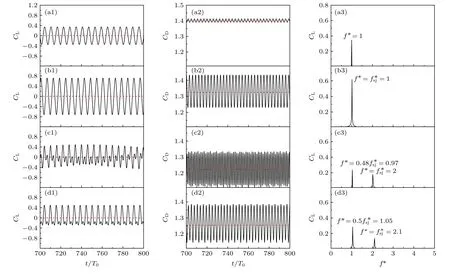
圖8 不同控制參數下流體動力參數的時頻域特性 (a) 未施加控制時;(b) =1,Δ?=π;(c) =2,Δ?=π;(d) f=2.1,Δ?=0.5πFig.8.Time history and frequency spectra of the cylinder’s force coefficients: (a) Unforced case;(b) =1,Δ?=π;(c) =2,Δ?=π;(d) =2.1,Δ?=0.5π.

射流控制的減阻效果如圖9,結果表明,射流控制可以減小圓柱的平均阻力.頻率相同時,在基本鎖頻區,平均阻力隨相位差增加而增加,在第二鎖頻區,平均阻力隨相位差增加而減小.大多數情況下,第二鎖頻區的平均阻力小于基本鎖頻區.

圖9 不同控制參數下圓柱的平均阻力系數Fig.9.Time-averaged drag coefficients under a range of control parameters.

4.2 相位差對聲輻射遠場的影響

接收點聲壓由各階聲源輻射出的聲波線性疊加得到,因此聲波的強度,頻率和相位至關重要.在本文所研究的低馬赫數條件下,可以忽略四極子的影響,遠場聲輻射由單極子和偶極子共同決定.單極子聲源和偶極子聲源指向性的區別在于,不考慮Doppler 效應的情況下,單極子聲源向四周均勻輻射聲波,而偶極子聲輻射則與聲源和接收點的相對位置有關,具有cosθ型的指向性.對于層流條件下的圓柱繞流問題來說,遠場聲輻射與流體動力脈動有關,聲場以升力偶極子占主導.而施加射流控制之后,除了射流引起的圓柱表面流體動力改變外,射流本身也引入了額外的單極子噪聲[16],因此需要進一步研究聲場的變化.

首先關注施加不同相位差Δ?對圓柱繞流輻射噪聲的影響.以圓柱圓心作為坐標原點(0,0),在r'=75D0為半徑的圓上沿周向均勻布置了512 個接收點,利用混合方法計算聲壓.利用超過30 個周期的p'統計其均方根值來表示接收點處聲壓的大小.考慮到Doppler 效應,在低馬赫數條件下計算時,接收點的位置修正為:r=r'(1+Macosθ)[1],其中以x軸為θ=0°.圖10—圖13 中的結果表明,在本文選擇的控制參數范圍內,無論施加何種控制,流向的聲壓均被增強;大部分方向的聲壓都大于未施加控制時;聲輻射的指向性與單子聲源類似.出現此結果的原因主要包括: 首先從圖8 中可以發現,施加控制后,平均阻力雖然下降,但阻力脈動始終大于未施加控制時,所以水平方向的聲壓始終是增加的;其次,由于射流控制本身具有單極子聲源的特性,同樣會增加接收點的聲壓.因此會出現施加控制之后,輻射噪聲增強,指向性趨于單極子類型的情況.

圖10 中施加=0.9,Δ?=0.5π 控制時,聲指向性不再保持未施加控制時的對稱的特點,這一現象也與Inoue 等[16]直接模擬結果相同.Inoue 等[16]的研究認為,這是單極子與偶極子聲源存在相位差導致.從(8)式中可以發現,圓柱表面升阻力脈動產生了向各自方向上輻射的偶極子聲源,圓柱表面射流引起的流量變化產生了向四周均勻輻射的單極子聲源,兩種聲源線性疊加后形成聲場.由于相同大小的射流孔上下對稱排布,可以用射流瞬時速度和ua來表示流量變化.瞬時流體動力和射流速度和的變化曲線如圖11,發生頻率鎖定時,升力脈動峰值與ua的峰值同相位.需要說明的是此現象只在=0.9,Δ?=0.5π 的工況下出現,而非施加合成射流控制并發生頻率鎖定時的普遍現象.從圖11 可以發現,當尾渦從圓柱上方脫落時,升力為正,并向升力的正方向輻射負脈沖,負方向輻射正脈沖,此時ua為正,向外輻射正脈沖,導致升力負方向聲壓脈沖被增強;當尾渦從圓柱下方脫落時,升力負方向的聲壓脈沖同樣被增強.同時在Δ?=0.5π 條件下,ua引起的單極子聲源較強,因此疊加之后會在升力方向上表現顯著的非對稱性.

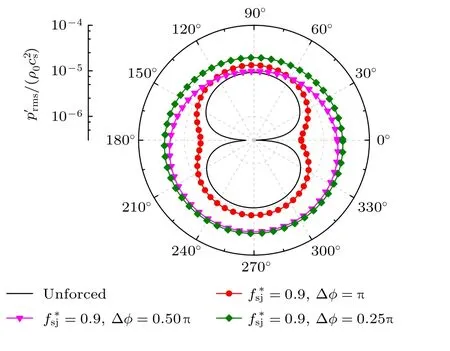
圖10 =0.9 時,不同相位差Δ? 在r'=75D0 范圍聲輻射指向性Fig.10.Directivity of the pressure p'rms measured at r'=75D0 with different Δ? when =0.9.

圖11 =0.9,Δ?=0.5π 時 (a) 圓柱升阻力與上下射流瞬時速度和隨時間變化曲線;(b),(c) 對應時刻聲源相互作用示意圖Fig.11.(a) Instantaneous lift coefficient,drag coefficient and ua,and (b),(c) Interaction between monopole and dipole when=0.9,Δ?=0.5π.

結合圖12 和圖13 可以發現,各個方向上最小聲壓大部分落在Δ?=π 的曲線上,聲壓隨著Δ?接近π 而減小.說明相同射流頻率下,相位相反的射流噪聲輻射水平最低.同時隨著Δ?從π 到0,聲輻射指向性逐漸由偶極子類型變為單極子類型.出現以上情況的原因在于施加射流控制后,聲輻射遠場由升力偶極子占主導變為射流單極子占主導,但Δ?=π 時,上下射流產生的單極子相位相反并互相抵消,此時射流單極子噪聲源也被消除.

圖12 =1.1 時,不同相位差Δ? 在r'=75D0 范圍聲輻射指向性Fig.12.Directivity of the pressure p'rms measured at r'=75D0 with different Δ? when f=1.1.

圖13 =2.1 時,不同相位差Δ? 在r'=75D0 范圍聲輻射指向性Fig.13.Directivity of the pressure p'rms measured at r'=75D0 for different Δ? when =2.1.

從流場來看,在基本鎖頻區,增大相位差Δ?時減阻效果減弱,在第二鎖頻區,增大相位差Δ?時減阻效果增強;從聲場來看,射流頻率相同時,使得相位差Δ?至π 能獲得最小的輻射聲壓.

4.3 射流頻率對聲輻射遠場的影響

射流頻率主要影響頻率鎖定的區域,當射流頻率在自然渦脫落頻率附近時,頻率鎖定發生在基本鎖頻區.當渦脫落頻率為射流頻率的1/2 倍時,頻率鎖定發生在第二鎖頻區.處在不同鎖頻區的流體動力隨控制參數變化規律不同.

當頻率鎖定發生在相同鎖頻區域且相位差一定時,增加射流頻率對聲輻射指向性的影響不大,如圖10 和圖13.當頻率鎖定發生在不同區域時,如圖12 和圖13,處于第二鎖頻區的工況向各個方向的輻射聲壓均大于基本鎖頻區的工況.

進一步的,固定相位差為Δ?=0.5π,改變控制頻率,如圖14.處于第二鎖頻區域的工況,在各個方向的輻射聲壓均大于處于基本鎖頻區的工況,且隨著頻率增加,聲輻射指向性趨于單極子類型.這是由于遠場輻射聲壓由升阻力脈動和射流速度脈動共同決定.在(8)式中,獲得單極子聲源需要求射流法向速度對時間的一階導數,因此,增加射流頻率一定會提升單極子聲源的輻射強度.同時在圖8 中,隨著控制頻率增加,頻率鎖定區域發生變化,導致升力脈動減小,阻力脈動變化不大,因此升力偶極子減弱.王成磊等[8]使用不同強度的射流獲得了更全面的發生頻率鎖定的參數組合,本文流體動力脈動的變化規律與其結論基本一致.綜合單極子聲源和偶極子聲源的變化來看可以發現: 隨著射流頻率增加,遠場聲輻射趨于單極子聲源的指向性,同時還會造成輻射噪聲增加.

圖14 Δ?=0.5π 時,不同射流頻率 在r'=75D0 范圍聲輻射指向性Fig.14.Directivity of the pressure p'rms measured at r'=75D0 with different when Δ?=0.5π.

最后通過聲功率級來評估合成射流對圓柱聲輻射遠場的影響大小,聲功率的表達式[37]為

其中聲強Ia通過進行計算;θ為以圓柱圓心為極點;x軸正方向為極軸的極坐標系下接收點的極角.以未施加控制時圓柱輻射噪聲的聲功率Wref a 為參考值,可以獲得聲功率級:

聲功率級隨控制參數變化如圖15 所示.施加控制之后,聲功率級均大于零,表明施加控制之后遠場輻射噪聲水平提高.射流頻率相同時,聲功率級隨相位差接近π 而減小,相同相位差下,聲功率級隨控制頻率增加而增加.在本文選取的控制參數變化范圍內,最大的聲功率級約為18 dB,最小的聲功率級約為4 dB.聲功率級與射流瞬時速度和的幅值隨控制參數的變化趨勢一致,表明施加控制之后,遠場輻射的噪聲水平主要受射流產生的單極子噪聲影響.

圖15 不同控制參數下圓柱輻射噪聲的聲功率級Fig.15.Acoustic power level measured at r'=75D0 under a range of control parameters.

5 結論

本文開展了合成射流對圓柱繞流近壁流場及聲輻射遠場的影響研究,主要獲得了以下結論:

1) 采用本文在忽略四極子條件下推導得到的適用于緊致聲源的聲比擬方程二維時域解,可以快速準確地求解包含周期性速度流入流出的固體邊界輻射噪聲問題.

2) 合成射流控制會對圓柱繞流輻射噪聲的指向性產生顯著影響,增加射流頻率或調控相位差遠離π,均能使輻射聲場的指向性由偶極子類型轉變為單極子類型.

3) 使用合成射流控制對圓柱實現減阻時,會在大部分方向上增強噪聲輻射.以未施加控制時的圓柱輻射噪聲作為參考,遠場輻射噪聲的聲功率級在4 到18 dB 范圍內變化.同時在阻力方向上,無論控制參數如何變化,聲壓始終增加.

4) 高頻射流的輻射噪聲更強,且更難出現頻率鎖定.在相同射流頻率下,增大相位差Δ?至π 能獲得最小的輻射聲壓.

因此,為了在減小流動阻力的同時不顯著增加輻射噪聲,可使射流頻率設置在基本鎖頻區,并將相位差設置為π.