基于信息熵與迭代因子的復雜網絡節點重要性評價方法

汪亭亭 梁宗文 張若曦

(西南石油大計算機科學學院,成都 610500)

在復雜網絡的研究中,如何有效地衡量節點的重要性一直都是學者們關心的問題.在節點重要性研究領域,基于拓撲學信息來判斷節點重要性的方法被大量提出,如K-shell 方法.K-shell 是一種尋找可能具有重要影響力節點的有效方法,在大量的研究工作中被廣泛引用.但是,K-shell 過多地強調了中心節點的影響力,卻忽視了處于網絡外圍節點作用力的影響.為了更好地衡量網絡中各個節點對傳播的促進作用,本文提出了一種基于迭代因子和節點信息熵的改進方法來評估各個層次節點的傳播能力.為評價本文方法的性能,本文采用SIR 模型進行仿真實驗來對各節點的傳播效率進行評估,并在實驗中將本文算法和其他算法進行了對比.實驗結果表明,本文所提方法具有更好的性能,并且適合解決大規模復雜網絡中的節點重要性評價問題.

1 引言

在網絡科學領域中,研究節點重要性的排序算法一直都是學者們追隨的熱點話題,其目的是為了通過對節點的重要性排序尋找出對傳播起關鍵性作用的節點.在病毒網絡中通過對重要節點的及時控制可以抑制病毒大面積的擴散[1],在社交網絡中,商家可以把新產品投放到重要客戶中,通過重要客戶的宣傳實現投資效益最大化[2].由此可以看出研究網絡中的重要節點不僅有重要的理論意義,更有重要的現實意義.

目前已經提出了各種方法來對節點的重要性進行排序.在網絡結構拓撲基礎上發展起來的經典算法有度中心性(DC)[3]、介數中心性(BC)[4]、接近中心性[5]和h指數[6]等,這些都是基于網絡拓撲結構的經典算法[7].另外,pagerank[8]和leaderank[9]是基于隨機游走的兩個代表性方法.Kitsak 等[10]提出了K-shell 方法,該方法的算法實現非常簡單,有研究顯示該算法對識別影響力節點具有顯著的度量作用[11].但是K-shell(ks)索引對網絡拓撲全局信息要求較高且在單調性(排名列表中擁有相同排名節點的比例)上表現不佳[12],即在同一個Kshell(ks)值中的所有節點都擁有相同的排名,這樣不利于唯一地區分節點的排名.之后研究者們在K-shell 基礎上提出了很多改進的方法.Basaras 等[13]提出了基于混合度和K-shell 的算法,該方法提出了μ冪社區指數(μ-power community index,μ-PCI).它是K-shell 和中心度的混合,該算法以完全局部化的計算方式達到了適用于任何類型的網絡.Wang 等[14]利用k-shell 的迭代信息來區分具有相同ks 值的節點,并同時考慮了節點度來綜合量化節點的重要性,具有很好的準確性.網絡中少量的節點具有大量的邊,這些節點也被稱為“富節點”,它們會出現傾向于彼此之間相互連接的現象,這種現象一般被稱為富人俱樂部現象[15].如果通過排序方法選出來的重要節點作為種子節點,種子節點之間具有高度連接,就會受富人俱樂部現象的影響,造成大量的活躍節點在傳播時出現交叉現象,傳播僅在小范圍內擴散.而這些以K-shell 為基礎的排序方法,往往無法避免網絡中富人俱樂部現象帶來的影響.

有研究學者已經提出很多方法來規避富人俱樂部現象的帶來的影響,使得基于拓撲排序的方法變得更可靠.針對富人俱樂部現象問題,Wang 等[16]提出一種改進的K-shell 方法(improved K-shell method,IKS),該方法通過迭代篩選出K-shell 各層中信息熵最高的節點,從而有效地避免富人俱樂部現象,實驗表明其對網絡中前K 個節點的傳播影響力衡量更準確.但在同一shell 內有大量信息熵相等的節點時,該算法會隨機選取其中之一并把其余節點投入到下次迭代當中,這就造成了本來排名靠前的節點因無限迭代而靠后.在Zareie 等[17]所提出的算法中考慮了節點及其鄰域集的公共層次,將迭代因子(iteration,IT)應用于網絡分層中,使得網絡中節點更具有差異性,從而提出一種基于鄰域相關系數的關鍵節點識別算法.

受Zareie 等[17]所提算法的啟發,本文沿用迭代因子(iteration,IT)對網絡進行分層;在改進的K-shell 方法(improved K-shell method,IKS)[18]的基礎之上,利用迭代因子來對網絡的結構進行分層,然后再分別計算每層中節點的信息熵,提出了基于迭代因子和信息熵相結合的方法(簡稱IE+)來衡量網絡中的節點重要性,該方法對在迭代過程中因隨機選擇造成節點排序靠后的問題有所改進,同時在具有富人俱樂部現象的網絡中進行節點重要性排序時也具有較好的表現.本文在八種常見網絡數據中使用SIR 模型[18,19]來模擬病毒傳播的過程,將所提出的算法與常見算法進行比較,實驗結果表明,本文所提方法具有更好的性能,并且適合解決大規模復雜網絡中的節點重要性評價問題.

本文的其余部分安排如下.第2 節簡要敘述了現有的一些經典算法.第3 節中將詳細闡述本文的算法思想.數據集將在第4 節中介紹.第5 節將簡要介紹評價指標.實驗設置、結果和討論在第6 節中提及.最后,在第7 節中給出結論.

2 相關工作

一個無向未加權網絡通常表示為G=(V,E),其中V和E分別表示節點和邊的集合.它也可以定義為一個鄰接矩陣A=(aij)n×n,如果節點vi和vj有一條邊相連接,則aij=1,否則aij=0.

大部分算法都是基于拓撲結構,關注節點的中心性.此前學者們提出了許多中心性度量方法,這些方法從不同的角度衡量了節點的重要性.在這里,簡要回顧幾個中心性指標的定義.

在度中心性算法中,DC 算法[3]主要考慮了節點度中心性,并得出節點鄰居數量越大傳播能力越強;接近中心性(CC)[5]算法則更關注節點和整個網絡之間的關系,認為節點與網絡中所有節點之間距離的平均值越小,節點越重要;學者們還提出了相對新穎的方法,例如基于重力的方法論上,取兩個節點的ks 值作為質量,兩個節點之間的最短路徑作為距離[20,21],兩個節點之間的相互作用關系隨著他們的距離而減小,模仿重力公式將兩個節點間的ks 值的乘積與兩節點間的最短距離的比值作為衡量節點傳播能力的度量,從而實現對節點重要性的排序.

Kitsak 等[10]提出了K-shell 方法,該方法認為節點的影響力是由它的位置決定的,而最有影響力的節點應該是網絡的核心.K-shell 分解是一個迭代過程,第一步是刪除所有度數為1 的節點,直到網絡中沒有度數為1 的節點,被移除節點ks=1.第二步是從網絡中移除所有度數為2 的節點,直到網絡中沒有度數為2 的節點,被移除節點ks=2.迭代繼續,直到所有節點都從網絡中刪除.圖1 列出了一個包含26 個節點和32 條邊的網絡圖.通過K-shell分解得到每個節點的ks 值.K-shell 算法認為ks值越大,傳播影響越大.這意味著在圖1 所示網絡中,節點1,2,3,4,5 的影響力最大,而ks=1的節點傳播影響力最小.在K-shell 的分解過程中,對度很大但位于網絡邊緣節點的影響力衡量不夠準確,例如圖1 中的節點21.研究人員基于K-shell提出了大量的擴展方法,如鄰域核心中心性(Cnc)、擴展鄰域核心中心性方法(Cnc+)[22]等算法認為,一個節點的影響不僅取決于它的自己的ks 值,也依賴于其鄰居節點的ks 值.

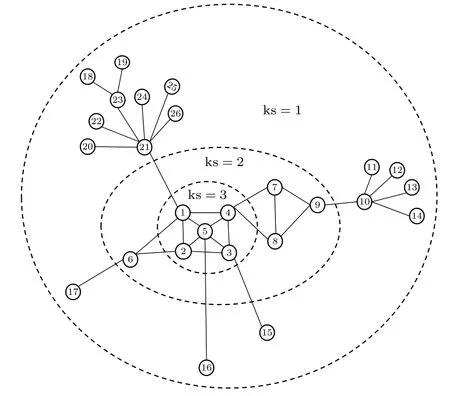
圖1 一個簡單示例圖Fig.1.A sample graph.

最近,一些混合的度量方法被陸續提出.這些方法充分利用節點的拓撲信息,利用混合的衡量指標從不同的角度來對節點的重要性進行評價.Bha 等[23]提出提高的混合排序方法,該方法結合了兩個中心性—擴展的鄰居中心性(Cnc+)和h指數中心性,該方法在排序準確性上具有很好的性能.阮逸潤等[24]提出了基于結構洞引力模型的改進算法,綜合考慮節點h指數、節點核數以及節點的結構洞位置.

除此之外,在動態網絡中,網絡拓撲隨著時間的推移而不斷變化,導致動態網絡中關鍵節點的識別變成一項艱巨的任務.研究者們通過不同時間段的網絡快照信息對節點進行排名[25-30],Qu 等[31]提出時態網絡中的時態信息收集(TIG)過程,將TIG過程作為節點的重要性度量,可用于節點重要性排名.胡鋼等[32]依托復雜網絡的層間時序關聯耦合關系、層內連接關系和層間逼近關系構建時序網絡超鄰接矩陣,提出了基于時序網絡層間同構率動態演化的超鄰接矩陣建模的重要節點辨識方法.

無論是靜態網絡還是動態網絡,它們都遵循冪律網絡中的一個重要性質就是少數幾個節點連接數量較多,而連接數量較多的節點更愿意去連接比它連接數量更多或同等多的節點,這時就造成了富人俱樂部現象的出現.為了避免富人俱樂部現象對排序結果帶來的影響,Liu 等[27]提出了一種基于每個節點的局部索引秩(local index rank,LIR)的算法,可以對具有富人俱樂部現象的網絡中的節點實現快速排序;Namtirtha 等[28]提出了一種混合指標的度量方法,考慮了節點的度、節點間的聯合影響率和節點間的最短距離,從網絡中心到網絡邊緣來對節點進行排序;改進的K-shell 算法[16]采用K-shell 分層與節點信息熵相結合的方法來迭代地選取重要節點,考慮了不同shell 層中網絡節點的重要性,但該算法會在具有相同信息熵的節點中隨機選擇一個并把其余節點投入到下次迭代當中,這就造成了本來排名靠前的節點因無限迭代而靠后.受IKS 算法的啟發,本文提出了一種基于迭代因子和信息熵的算法來識別從網絡外圍到核心的每個網絡級別的重要節點,將此方法簡稱為IE+.

3 算法介紹

3.1 迭代因子

在IKS 方法中,網絡使用K-shell 進行分層.從圖1 可以看出,雖然節點7,8 和9 在同一個K-shell中,但是節點7,8 較節點9 更接近網絡的核心,當網絡中的節點被移除時,節點9 在節點7,8 之前被移除.與被感染的節點9 相比,被感染的節點7,8 可以達到更好的傳播效果.鑒于K-shell 對節點重要性度量不夠完善,本文提出迭代因子(iteration,IT)對節點進行分層,使得網絡層次結構更加清晰.

以圖1 為例,設置迭代因子的初始值IT=1,然后將度數最小的節點從網絡中移除.這些被移除的節點屬于圖結構的第一層,然后在本次迭代中被刪除節點的迭代因子IT=1.在下一階段,IT 值增加1,并再次從圖中刪除度最小節點,并將在本次迭代中被刪除節點的IT=2.這個過程會一直迭代,直到圖中沒有剩余節點.在每次迭代中,IT 的值都會加1 并分配給在此階段中被刪除的節點.從圖1可以看出,節點7,8,9 不再處于同一結構層級,但節點7 和8 更靠近網絡中心,因此比節點9 具有較大的IT 值.同理,對位于網絡中心的節點(如節點1,2,3,4,5)的網絡層次劃分更細,節點5 被認為是網絡的核心,節點1,2,3 和4 被認為是次要核心.

3.2 信息熵

在IKS 算法中,信息熵被定義為

其中j∈Γ(i) 是節點vi的鄰居節點的集合,其中:

從(1)式和(2)式可以看出,節點信息熵的計算主要依賴于節點的本地鄰居信息.節點17,18和19 都在網絡的外圍,如果僅依靠鄰居的度信息來計算節點的信息熵,那么這三個節點的信息熵和ks 值均相同.但節點17 的鄰居節點比其他兩個節點的鄰居節點更接近網絡的中心,因而僅依靠鄰居節點的度信息顯然是不夠的.因此,本文結合節點在網絡中的位置,基于ks 提出一種計算節點信息熵的新方法:

其中 (i) 是節點vi的鄰居集合;Ij的定義如(2)式所示;ksj表示節點j的ks 值.以節點17 為例計算其信息熵:

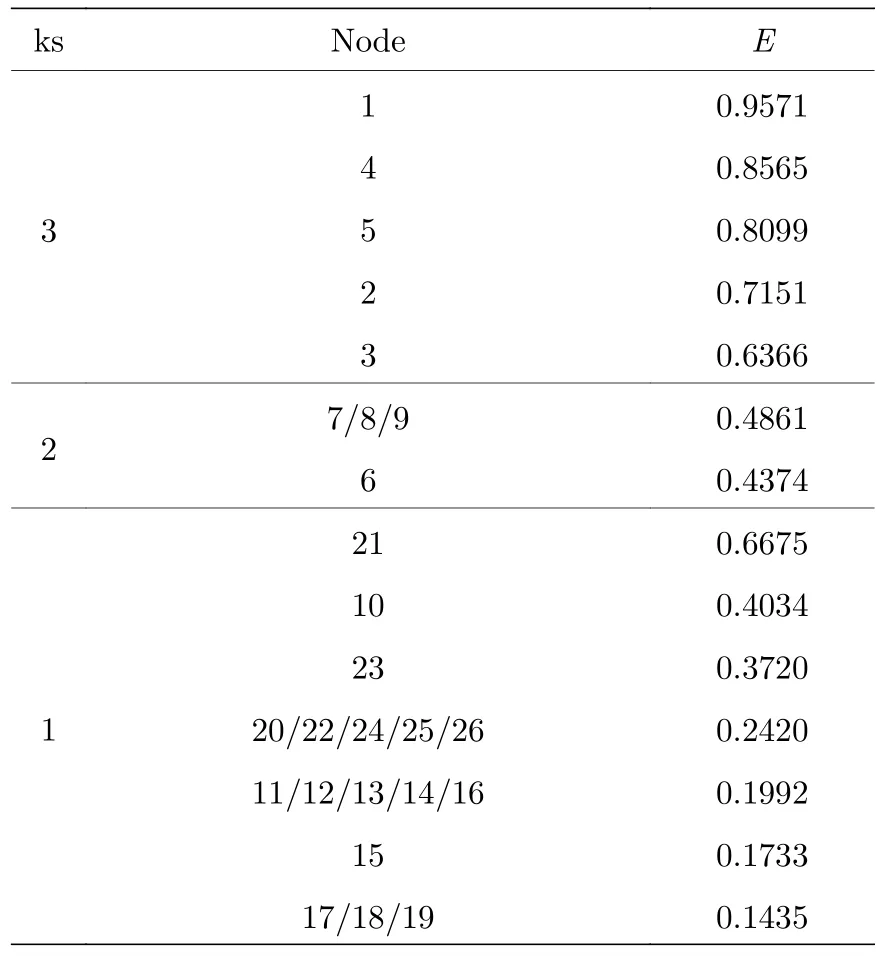
表1 節點在每個shell 中的信息熵Table 1.Information entropy of each node.

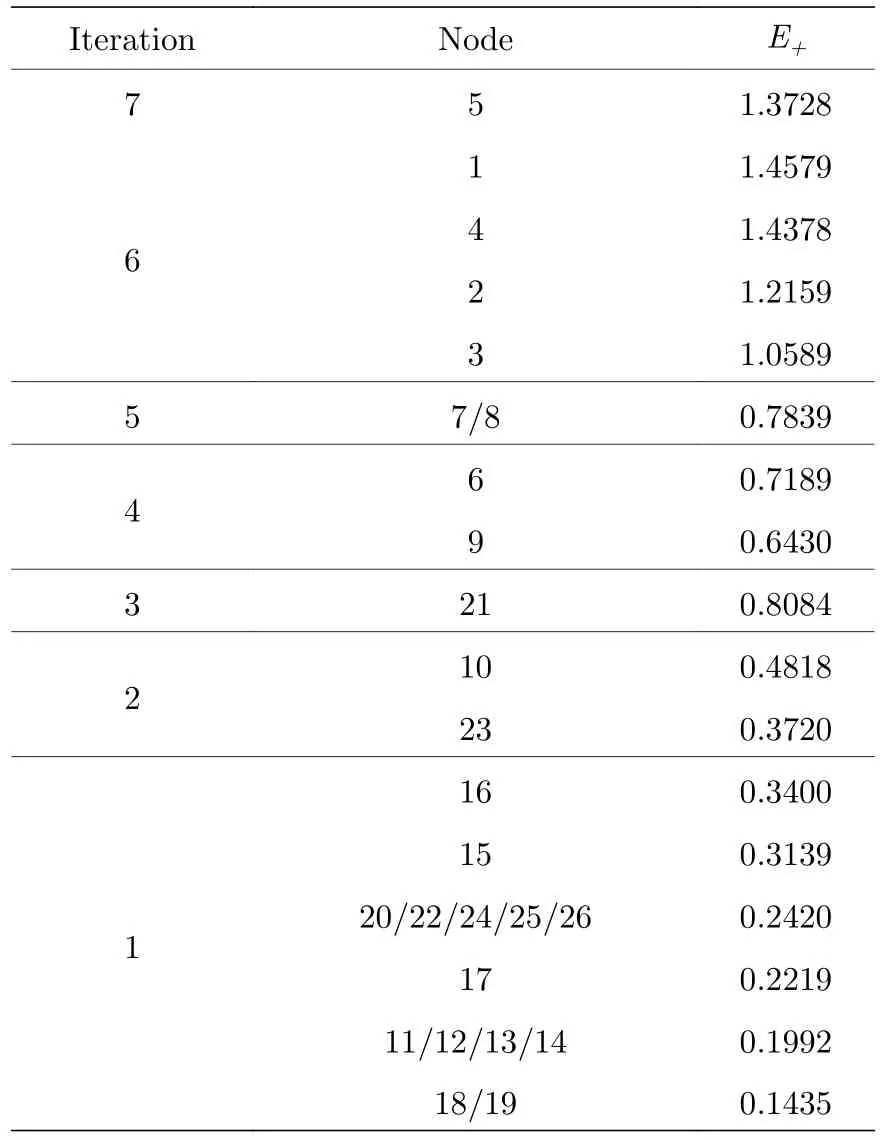
表2 節點在每個迭代層中的信息熵Table 2.Information entropy of each node.

3.3 算法步驟

本文基于迭代因子(IT),通過ks 值對節點信息熵的計算進行改進,提出了迭代因子和信息熵相結合的算法(簡稱IE+)來對節點的重要性程度進行度量,該算法的步驟如下:

1) 使用K-shell 算法計算網絡中所有節點的ks 值,然后令IT=1;

2) 將當前網絡中度最小的節點的迭代因子記為IT,并根據(4)式來計算這些節點的信息熵 ei+;

3) 從網絡中刪除這些度最小的節點;

4) 若網絡中的節點個數為0,記錄IT(max)=前迭代因子IT,跳轉步驟5;否則,IT 加1,跳轉步驟2;

5) 選擇當前迭代因子IT 對應節點集合中信息熵最大的節點,按序放入節點重要性排序集合中.如果有多個節點信息熵值相等時,按照節點的序號從大到小將所有信息熵相等的節點全部放入重要性排序集合中;

當今，大部分高中學生在學習數學內容時都喜歡用單一的思維去審視和理解課本，而且都采用的是比較陳舊的方法來解答習題，在解題思維上顯得比較呆板，缺乏變通.而習題又是教師對學生傳達自己解題步驟和核心技巧的載體，所以提高學生的解題能力至關重要.

6) 如果IT=0,則跳轉步驟7,否則IT 減1,跳轉步驟5;

7) 如果網絡中所有節點都已經被放入重要性節點排序集合中,則結束算法;否則,令前迭代因子IT=IT(max),跳轉到步驟5.

算法偽代碼如下所示:

計算出每個節點的ks 值和迭代因子IT 后,將迭代因子相同的節點按照信息熵值降序排列,如表2 所列.然后對節點進行排序,在最大迭代因子中選擇最大信息熵的節點,顯而易見應該選擇節點5,然后在下一個迭代因子中選擇節點1.在下一層中節點7 和8 具有相同的改進的信息熵值.按節點序號從大到小順序放入,直到最小的迭代因子層次結構中選擇信息熵最大的節點.此時,第一次迭代結束,下一次迭代繼續從迭代因子最高中選擇節點,直到所有節點都被選中.

在表3 中,使用了不同的方法對圖1 中的網絡進行排序.因為每種方法對節點重要性的識別原理不同,可以看出每種方法的排序結果略有不同.與IKS 算法相比,在迭代次數相同的情況下,本文算法識別出的重要節點在網絡中的分布更廣,這表明本文算法能更有效地避免在迭代次數相同時出現的富人俱樂部現象.

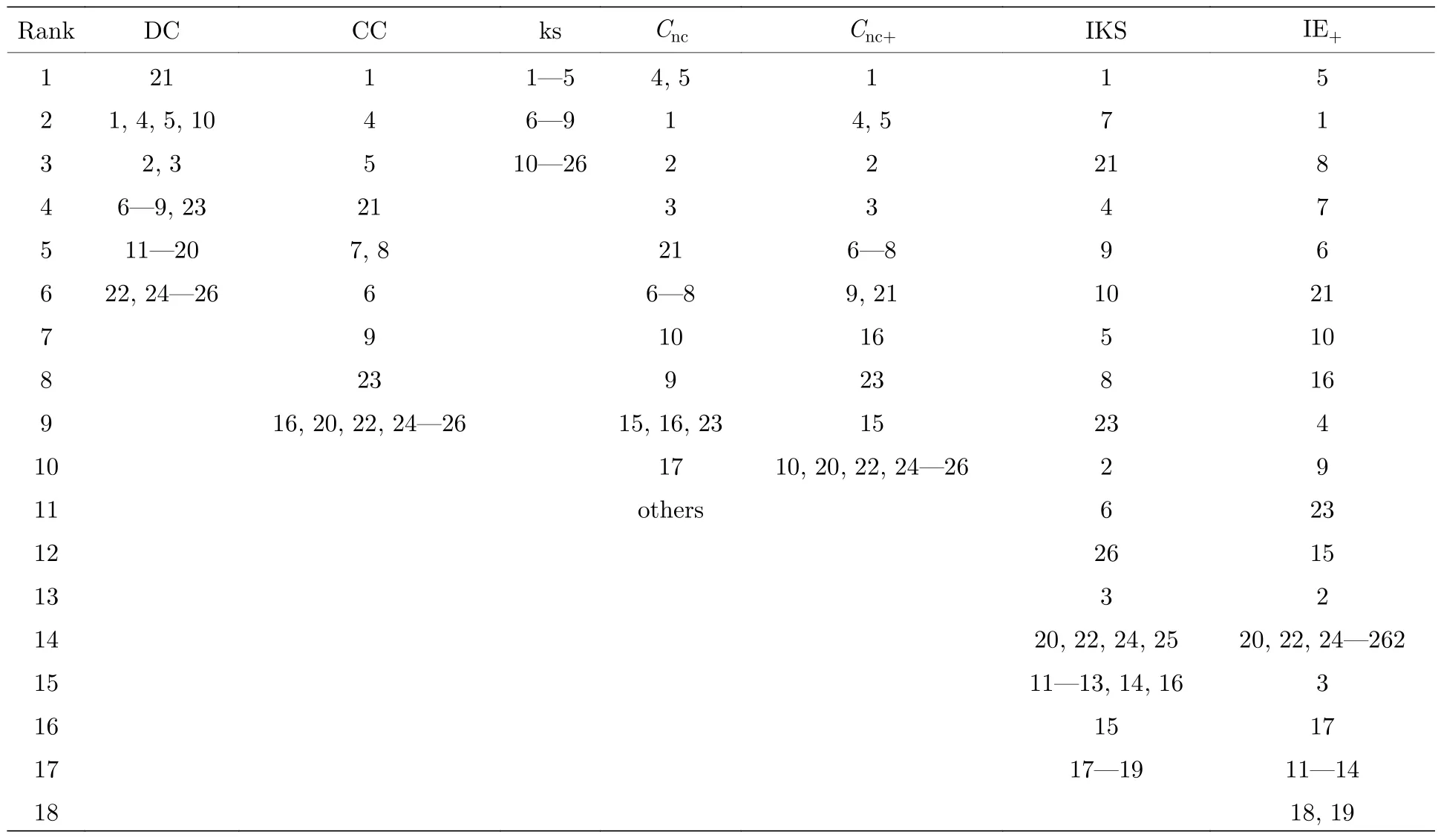
表3 由不同方法得出的排名: DC,CC,ks,Cnc,Cnc+,IKS,IE+Table 3.The ranking lists determined by different methonds: DC,CC,ks,Cnc,Cnc+,IKS,IE+.

4 數據集

選擇了八種不同類型的網絡,其詳細信息見表4.1) NS 是一個由從事網絡科學工作的科學家組成的合作網絡[33].2) EEC 描述了一家大型歐洲研究機構成員之間的電子郵件交換[34].3) PB 是美國政治博客的網絡[35].4) Facebook 描述了該網站的社交圈[36].5) WV 是一個維基百科網絡,描述了投票記錄[37].6) Sport 是從體育網絡收集的有關Facebook 頁面上的體育運動的信息(2017 年1 月)[38].7) Sex 是一個二分網絡,其中節點是女性和男性.當男性寫帖子表明與女性發生性接觸時,他們之間的聯系就會建立起來[39].8) CondMat 是一個協作網絡,涵蓋了凝聚態類別中作者論文之間的科學合作關系[40].

5 評價指標

5.1 SIR

在本文中,使用SIR 模型[18,19]來驗證算法的表現能力.通過模擬SIR 模型的傳播過程,可以得到每個節點的傳播能力.在SIR 模型中,每個節點可以具有三種狀態,即易感狀態、感染狀態和恢復狀態.一開始,網絡中的所有節點都處于易感狀態,除了原始的受感染節點.在每個時間段中,每個被感染的節點都會以β的概率感染那些處于易感狀態的鄰居節點.同時,受感染節點將以λ的概率進入恢復狀態并不會再次感染,當網絡中沒有受感染節點時,此傳播過程結束.在選擇傳播值β時,它可以略大于網絡流行閾值βth=〈k〉/〈k2〉,其中k是平均度,k2是二階平均度[41].不同網絡中的βth和βc值如表4 所列.當網絡達到穩定狀態時,記錄恢復的節點總數,可以用來衡量節點的傳播能力,對每個節點重復該過程來衡量它的傳播效率.為了獲得更準確的實驗數據,SIR 模型傳播過程的模擬次數由網絡規模決定,在N＜104的小型網絡中模擬次數為1000 次,在N≥ 104大型網絡中模擬次數為100 次.

表4 八個常見網絡的基本拓撲特征,N 和|E|是節點和邊的數量,〈d〉 和〈k〉 是平均距離和平均度,c 是聚類系數,βth 和βc 是流行閾值和傳播值Table 4.The basic topological features of the eight real neworks,N and |E|,|E| are the number of nodes and edges,〈d〉and〈k〉 are the average distance and the average degree,c is the clustering coefficient,βth and βc are the epidemic threshold and the spread value.

5.2 相關系數

為了驗證本文算法的性能,使用Kendall Tau[42]系數τ來衡量不同算法得到的節點重要性排名表與SIR 模型模擬的排名表之間的相關性,τ定義為

其中Nc和Nd分別是經過計算后相關性一致和不一致的數量.考慮具有N個節點的兩個相關序列X和Y,X=(x1,x2,···,xn)和Y=(y1,y2,···,yn).任何一對二元組(xi,yi)和(xj,yj)(x≠y),當xi＞xj和yi＞yj或xi＜xj和yi＜yj這兩個元素被認為是一致的,如果xi＞xj和yi＜yj或xi＜xj和yi＞yj它們是不一致的,如果xi=xj或yi=yj時不計入Nc和Nd.系數必須在—1 ≤τ≤ 1 的范圍內,τ值越大,算法的排序結果越接近準確值.

5.3 單調關系

一個好的節點重要性排序算法應該是每個節點都被分配唯一的排名索引,如果在同一排名索引上出現多個節點,那么這樣的算法被認為是存在缺陷的.為了定量測量不同指標的分辨率,使用了排名列表的單調性指標M(R)[22]:

其中Nr是具有相同索引值r的節點數.如果M(R)=1,表示該算法是完全單調的,并且每個節點被歸類為不同的索引值,如果M(R)=0,則所有節點處于同一等級.單調性指標反映排序算法是否能很好地將節點區分開來.

5.4 平均最短路徑長度

計算每對傳播者之間的平均最短路徑長度[43],這是一個基本指標.如果每個節點感染其他節點的概率相同,則初始感染節點越分散,傳播范圍越廣.本文選擇初始節點S作為度量,其定義為

其中|S|和S 分別表示選擇的種子節點的數量和選擇的初始節點集合;duv是從節點u到節點v的最短路徑的長度.

6 實 驗

6.1 相關系數

在表5 中顯示了所提出的方法以及其他索引方法與SIR 模型模擬得出的排名R之間的Kendallτ秩相關系數,在表中加粗字體對應最優值.從表5可以看出經典DC 網絡算法的性能并不太理想,在Sex 網絡中,雖然IE+算法表現不是最佳,但與最優值對應的算法Cnc+相比相差不大,盡管本文提出的IE+算法并不是在所有網絡中都表現最好,但在大多數網絡中比其他算法更具有表現力.

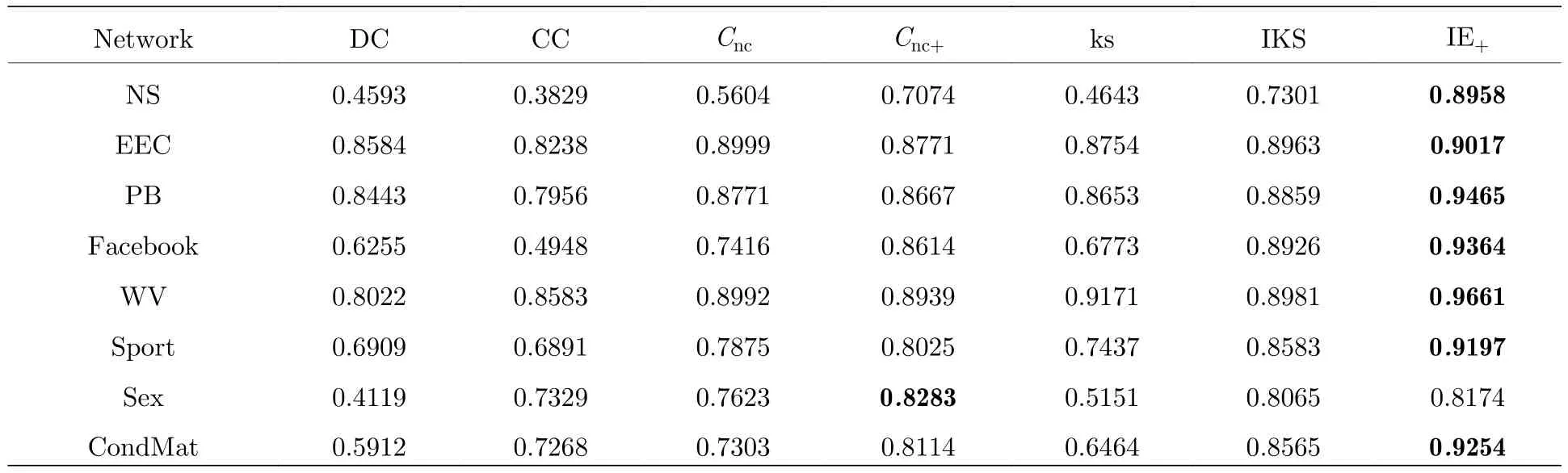
表5 SIR 模型中節點影響指數R 與五個中心性指數之間的Kendall TauTable 5.The Kendall Tau between the node influence index R of SIR model and five centrality indices.

6.2 單調關系

本文對各算法單調性進行了度量.算法的單調性越高說明該方法在確定唯一排名的能力越強,在表中加粗字體對應最優值.從表6 可以看出,在大多數網絡中,本文提出的IE+算法與IKS 方法相比單調性較強.雖然在一些網絡(如NS,EEC 等網絡)單調性上表現不是最佳的,但在較大網絡上本文算法單調性要比其它算法單調性要高.

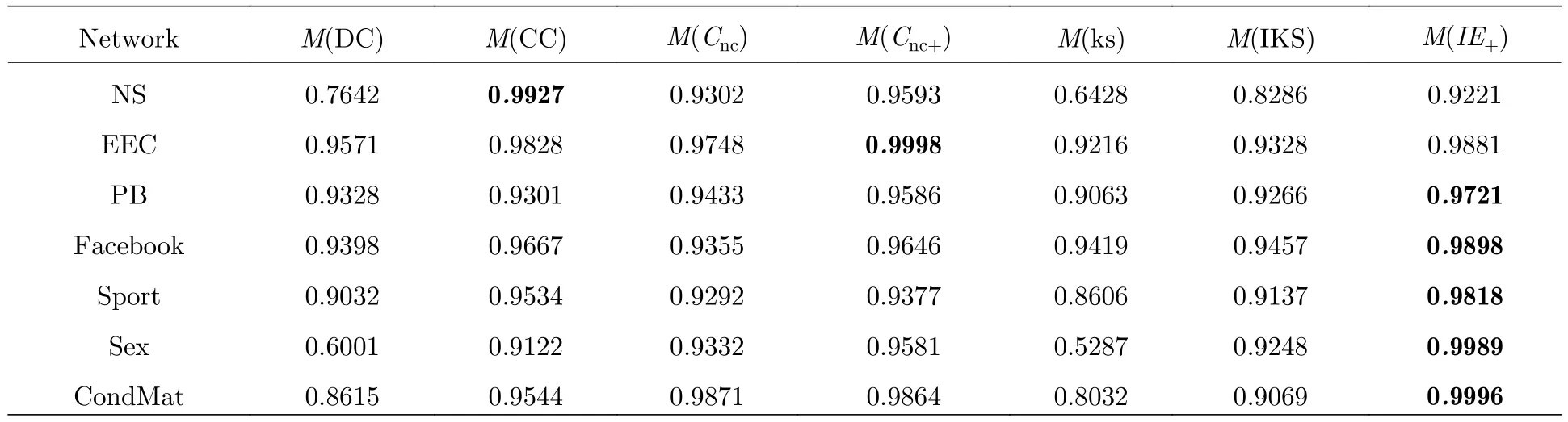
表6 不同排序方法的單調性 MTable 6.The monotonicity M of different ranking methods.

6.3 平均最短路徑長度

為避免富人俱樂部現象帶來的影響,將排序得到的重要節點作為初始感染節點,在傳播中當節點的感染概率相等時,為得到更廣的傳播范圍則需要更多的初始感染節點分散在網絡中.本文進一步測試了不同算法下不同比例的初始感染節點之間的平均最短距離.如圖2 所示,通過不同算法排序得出的節點集合,選取了前2%—20%的重要節點,發現,除了EEC 網絡,隨著初始感染節點的比例不斷擴大,重要節點之間的平均距離也在相應擴大.這更進一步說明了本文提出的IE+算法在避免富人俱樂部現象方面具有較為優秀的表現.

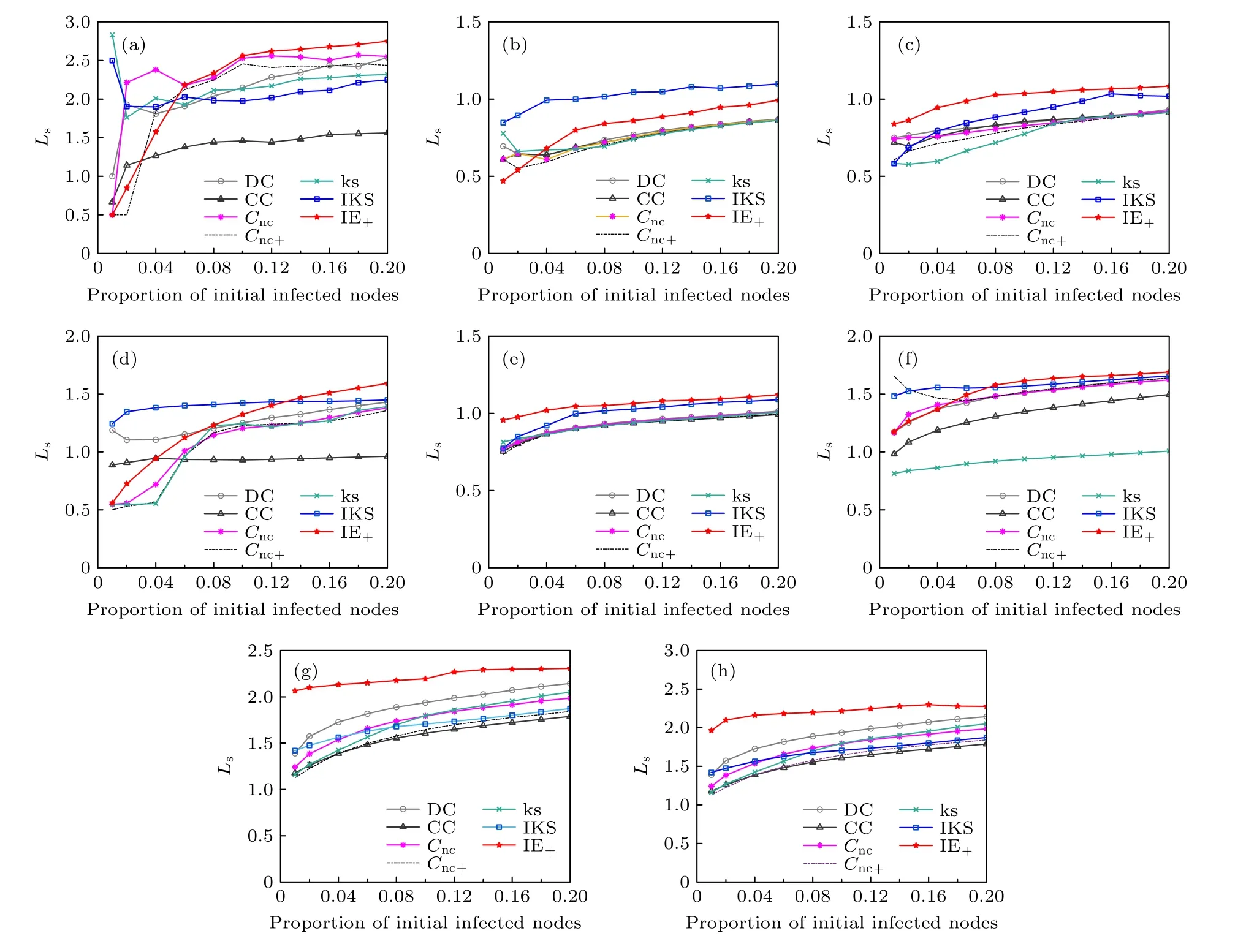
圖2 不同方法下不同比例源擴散器的平均最短路徑長度Ls (a) NS;(b) EEC;(c) PB;(d) Facebook;(e) WV;(f) Sport;(g)Sex;(h) CondMatFig.2.Average shortest path length Ls under different proportion of source spreaders by different methods: (a) NS;(b) EEC;(c) PB;(d) Facebook;(e) WV;(f) Sport;(g) Sex;(h) CondMat.

6.4 重要節點性能

對節點進行排序的最終目的是為了挖掘出對傳播過程起關鍵作用的節點,換句話說,如果通過排序算法得到的重要節點對傳播過程起不到很好的作用,那么這樣的排序算法是不可靠的.本小節中從不同角度來評判IE+算法識別的重要節點的在網絡傳播中的表現情況.因在此部分討論的是前k個重要節點在網絡中的傳播規模,本文引入一些個經典的影響力最大化算法(CI[44],CELF++[45],IRIE[46])作為比較算法.

在圖3 中,選擇網絡中排名靠前的2%—20%個節點,計算在感染值為βc=2βth,λ=1,t=20 時感染的節點總數(不包括初始感染節點)與網絡節點總數的百分比.我們驚訝地發現在大多數網絡中,在CC,Cnc+,ks,IKS 算法下,隨著種子節點數的增加,感染的節點總數反而在減少,這種現象是因為隨著種子節點越來越緊密地聚集在一起,它們開始重疊,無法再有效地傳播.而在NS,Facebook,Sex 和CondMat 網絡中,IE+算法隨著初始感染節點總數的增加相應的感染節點總數也在增加,在其余網絡中雖然IE+算法隨著初始感染節點的增加而略有下降,但下降趨勢相對緩慢.除EEC的其余網絡中,IE+算法優于經典的影響力最大化算法(CI,CELF++,IRIE),或與其表現出相同的優勢.

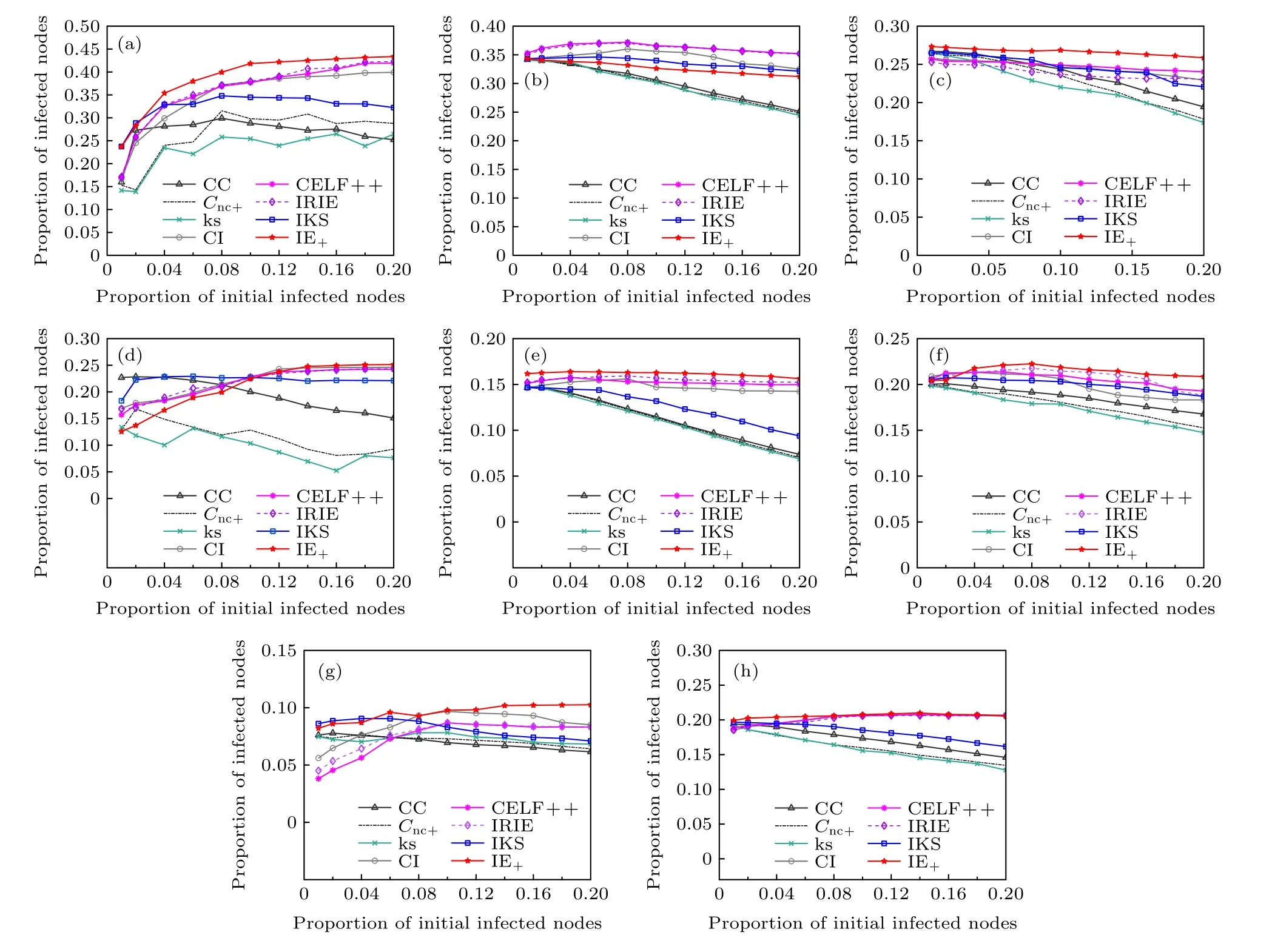
圖3 比較在相同時間內感染節點總數的百分比 (a) NS;(b) EEC;(c) PB;(d) Facebook;(e) WV;(f) Sport;(g) Sex;(h) CondMatFig.3.Compare the percentage of the total number of infected nodes over the same time period: (a) NS;(b) EEC;(c) PB;(d) Facebook;(e) WV;(f) Sport;(g) Sex;(h) CondMat.

在六個網絡中,通過各排序算法計算后,選擇排在前 10%的節點作為初始感染節點.在上述相同的感染概率和恢復率下,記錄不同傳播時間感染節點數與總節點數的百分比.從圖4 可以看出,隨著時間的增加,感染節點的數量先增加后趨于穩定,該現象是因為隨著傳播時間達到一定的時長時,網絡處于穩定狀態.在NS,Facebook,WV,Sport和CondMat 網絡中,本文提出的IE+算法具有最廣泛的傳播范圍.

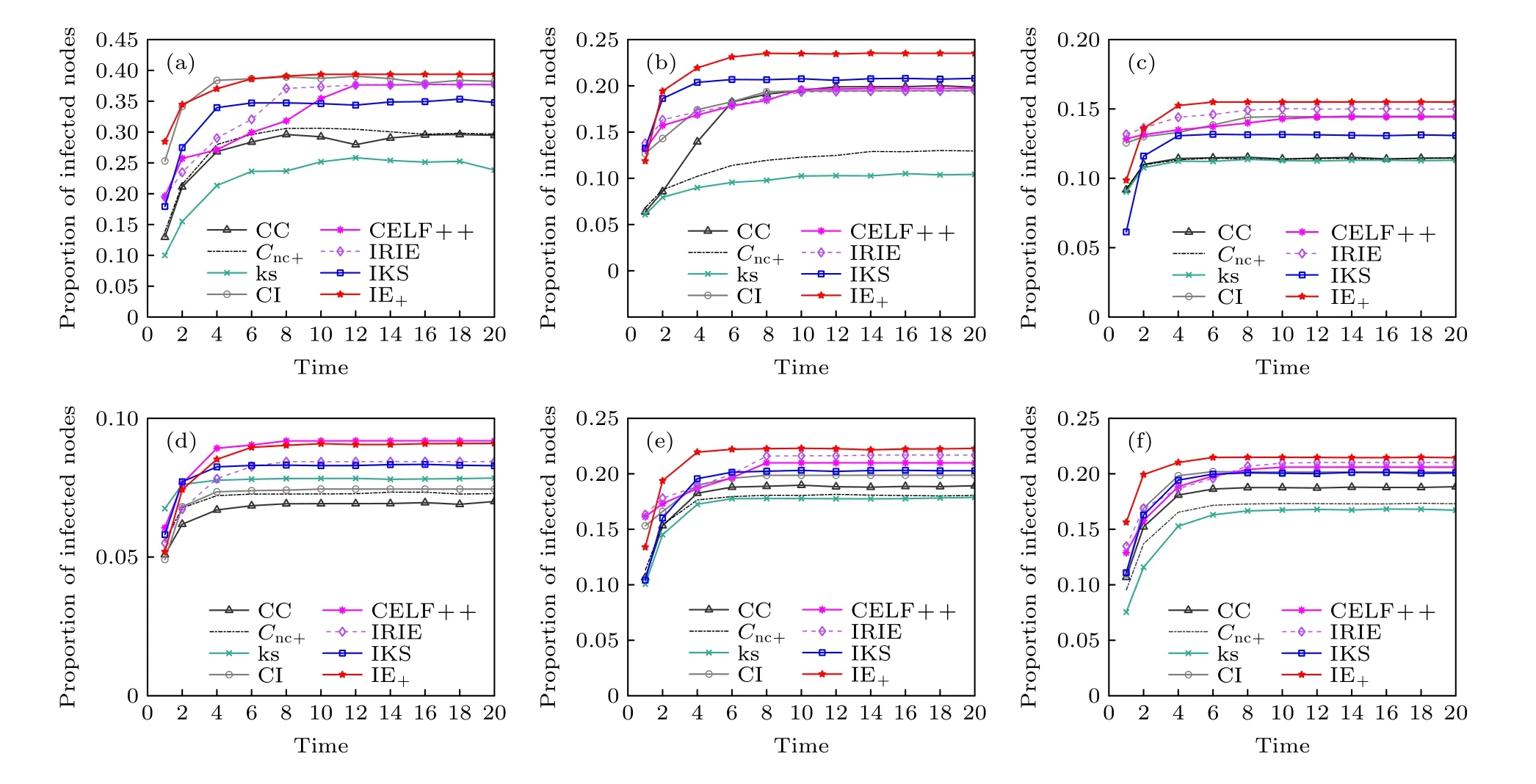
圖4 比較不同傳播時間 t 中前 10% 種子節點感染節點的百分比 (a) NS;(b) Facebook;(c) WV;(d) Sex;(f) Sport;(f) CondMatFig.4.Compare the percentage of nodes infected by the top 10% of seed nodes in different propagation time t: (a) NS;(b) Facebook;(c) WV;(d) Sex;(f) Sport;(f) CondMat.

6.5 時間復雜度

在時間復雜度方面,由于需要節點的ks 值來計算節點的信息熵,所以本文所提出的IE+算法的時間復雜度主要體現在迭代因子IT 和ks 值的計算上.計算節點迭代因子IT 和節點的ks 值的時間復雜度都是O(n),即本文算法的時間復雜度是O(n),IKS,Cnc,Cnc+,DC,ks 的時間復雜度都是O(n),CC 的時間復雜度為O(mn).因此,就時間復雜度而言,我們的算法并不比其他算法具有更高的時間復雜度.在相同的時間復雜度下,IE+算法在幾個考察指標上都具有良好的表現.

7 結論

在復雜網絡分析中,對節點的影響力進行識別和排序是一個基礎性工作.本文的研究目的是將信息熵與迭代因子相結合,提出一種新的節點影響力評價指標,通過排序算法得到的重要節點即使在受到富人俱樂部現象的影響下也依然具有很好的傳播效果,基于該指標,利用迭代因子和改進的信息熵,提出了衡量節點重要性方法IE+.通過在Kendall Tau 相關系數、單調性、平均最短距離以及節點性能上的對比實驗,表明本文提出的算法能有效對節點的重要性進行評估,并能很好地規避富俱樂部現象,對復雜網絡中的重要節點識別工作具有較強的借鑒意義.