云計算環(huán)境下的QR碼雙重加密復(fù)合數(shù)字水印算法

馬 婷，李 佳

(中國民用航空飛行學(xué)院 計算機學(xué)院，四川 廣漢 618307)

0 引言

在大數(shù)據(jù)以及網(wǎng)絡(luò)等技術(shù)取得了迅猛發(fā)展的背景下，應(yīng)運而生的云計算環(huán)境可以滿足對大數(shù)據(jù)的存儲及運算效力。云計算技術(shù)讓人們走進了信息共享時代，帶來便利的同時也產(chǎn)生了一定的弊端，大量的信息與此同時被轉(zhuǎn)載、盜用，因此上傳到云端數(shù)據(jù)的安全性就顯得格外重要。對于共享信息來說，要能夠?qū)ζ浒鏅?quán)提供有力保護，有效避免共享信息被盜用，信息隱藏領(lǐng)域的數(shù)字水印技術(shù)恰好在對上傳到云環(huán)境的數(shù)字產(chǎn)品版權(quán)保護方面是最好的選擇。

文獻[1-4]對聯(lián)合水印算法提出了不同思路的優(yōu)化。饒俊慧等[1]以聯(lián)合離散余弦變換(Discrete Cosine Transform，DCT)和奇異值分解(Singular Value Decomposition，SVD)(DCT-SVD)嵌入半脆弱水印的方法能更好地感知水印，得到了較好的穩(wěn)健性。王玉瑩等[2]以離散小波變換(Discrete Wavelet Transform，DWT)和DCT(DWT-DCT)為理論基礎(chǔ)，對一種復(fù)合水印算法做出了改進，改進后的算法在對常規(guī)攻擊問題的解決過程中，能夠取得極為出色的抵抗效果，從水印的安全性角度展開分析，算法能夠完成對水印信息的2次加密處理，使其具有極高的安全性。黃根嶺等[3]采用兩變換聯(lián)合對DWT-DCT-SVD三重聯(lián)合的水印方法進行了調(diào)整，使水印具有了更高的魯棒性。白浩印[4]和展虎等[5]對一種新的水印技術(shù)進行了研究并以非下采樣輪廓波變換(Non-subsampled Contourlet Transform，NSCT)為基礎(chǔ)，分別提出了DWT-Schur盲檢測和DCT-DWT-SVD四變換聯(lián)合，文獻[4]的盲檢測對水印的隱蔽性做了很好的處理，文獻[5]表明當受到濾波以及泊松噪音等攻擊時，該算法能夠展現(xiàn)出極強的抗攻擊穩(wěn)定性。文獻[6-7]借助二聯(lián)合變換來完成對水印的處理，并選用ZUC以及Arnold充當加密方法，使水印具有了更高的安全性。毛新光[8]在對水印算法的研究過程中，對快速響應(yīng) (Quick Response，QR) 碼進行了引入，以此來充當加密方法，從而為QR碼提供保護，使其穩(wěn)定性得到了提升。陳星娥等[9]在對SVD水印算法的研究過程中，對QR碼進行了引入，能夠清晰地提取QR碼。欒煒等[10]以DWT-SVD為理論基礎(chǔ)，在其雙重水印算法中引入了QR碼。吳強等[11]以DWT-FRFT為理論依據(jù)，在其雙重水印算法中引入了QR碼，在對水印圖像的提取過程中，部分圖像存在失真問題。張汝汝[12]以DWT-DCT-SVD為理論依據(jù)，在其三重水印算法中引入了QR碼，同時完成了對加密算法的優(yōu)化，并表示QR碼在安全領(lǐng)域中發(fā)揮著重要作用。文獻[13-15]對彩色圖像水印算法進行了研究，引入了QR碼，使算法具有了更高的穩(wěn)定性，證明QR碼具有極為廣泛的應(yīng)用范圍。

QR 碼被廣泛運用在各個領(lǐng)域中，人們可借助掃碼來快速對相關(guān)信息進行獲取，各類數(shù)據(jù)信息均可被存儲在QR碼中，同時具有極為強大的糾錯能力[7]，因此，在QR碼中引入水印技術(shù)之后，能夠使算法的穩(wěn)定性以及信息的嵌入量得到顯著提升。文獻[16-17]提出了NSCT，與輪廓波變換相比，NSCT不僅繼承了其相關(guān)優(yōu)點，同時在其他方面具有獨特優(yōu)勢。對于圖像分析來說，其使小波變換存在的缺點得到了有效彌補，不僅能夠使多尺度分析得到實現(xiàn)，同時還存在著平移不變性以及多方向異性等優(yōu)勢。在對SVD的使用過程中，可完成對圖像特征的解析，以SVD存在的相關(guān)特點為依據(jù)，其在水印算法中發(fā)揮著重要作用，不僅能夠使其魯棒性得到提升，還能夠提升其抵抗幾何攻擊的能力。

以上述分析為依據(jù)，針對云環(huán)境下數(shù)據(jù)安全性考慮，以應(yīng)用性較強的QR碼為理論基礎(chǔ)，提出了NSCT-DWT-SVD雙重加密復(fù)合數(shù)字水印算法，該算法可在多幅圖像的分析過程中發(fā)揮重要作用。對其展開仿真分析，以分析結(jié)果為依據(jù)，該算法可借助雙重加密使其安全性得到提升，同時還具有極高的透明性。不同于其他算法，該算法能夠大幅度提升魯棒性，為云計算應(yīng)用的數(shù)據(jù)安全、穩(wěn)固發(fā)展提供了可靠的保障手段。

1 基本理論

1.1 小波變換

小波變換是一種在時頻域能量較集中的變換分析方法，在傅里葉變換基礎(chǔ)上，發(fā)展了視頻局部化思想，并擁有一個根據(jù)頻率變換隨之變化的窗口，對信號頻域分析起到了較好的作用。小波變換的作用對象為數(shù)字信號，能夠?qū)ζ浞直媛室约八幍膮^(qū)域展開多尺度分析，假如f(x)∈L2(R)，則：

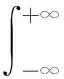
(1)

圖像離散小波函數(shù)為：

φj,k(x)=2jφ(2-jx-k)，

(2)

式中，j,k∈Z，尺度j與平移因子k是離散的。二維離散小波能夠被廣泛應(yīng)用在水印領(lǐng)域之中，以?f(x)離散小波變換為研究對象，可對其進行如下定義：

(3)

式中，離散小波的變換系數(shù)f(x)>=WTf(j,k)。

借助小波分析完成了對512 pixel×512 pixel Lena圖像的處理之后，對所獲取的系數(shù)進行了展示，如圖1所示，其由低頻以及高頻系數(shù)構(gòu)成，由于低頻聚集絕大部分的能量，可將水印嵌入到該部分之中，從而可確保圖像具有較高的穩(wěn)定性，細節(jié)信息被包含在高頻部分之中，對水印的嵌入具有較低的穩(wěn)定性，以小波變換為研究對象。

(a)近似值系數(shù)A1

(b)水平細節(jié)系數(shù)H1

(c)垂直細節(jié)系數(shù)V1

(d)對角細節(jié)系數(shù)D1圖1 對Lena圖像進行小波分解后的系數(shù)Fig.1 Coefficient of Lena image after wavelet decomposition

1.2 SVD

以SVD的理論基礎(chǔ)為特征解析，可在任意矩陣中完成對其擴充，假如通過矩陣A來對某個數(shù)字圖像進行表示，其屬于m×n型矩陣，對于SVD來說，其酉矩陣分別為U以及V，可將其視為正交矩陣，奇異值矩陣由S來表示，可將其視為半正定對角陣，則：

(4)

式中，S=diag(S1,S2,…,St),S1≥S2≥S3≥…≥St≥0，t為S的秩。

SVD在水印算法和機器學(xué)習等領(lǐng)域應(yīng)用也較多，主要是因為它具有較好的特征，部分特征如下：

① 轉(zhuǎn)置：無論是矩陣A，還是其轉(zhuǎn)置矩陣AT，存在完全相同的奇異值；

② 穩(wěn)定性：借助奇異值矩陣來完成對奇異值的調(diào)整，使其穩(wěn)定性得到提升；

③ 圖像的部分特征及內(nèi)部特征包含在奇異值中。

1.3 NSCT

在圖像分析領(lǐng)域中，與輪廓波以及DWT等變換相比，NSCT更具優(yōu)勢，不僅能夠使多尺度分析得到實現(xiàn)，同時還存在著高冗余性等優(yōu)點，在對水印信息的嵌入過程中，能夠?qū)Ω嗟男畔⑦M行保存，降低信息丟失的概率，防止子帶信息出現(xiàn)重疊的頻譜。以NSCT為研究對象，其主要包含兩大部分，框架圖如圖2(a)所示，首先是非采樣塔式濾波器組(Nonsubsampled Pyramid Filter Bank,NSPFB)，在完成了對低頻帶通部分的分解之后，該部分無需通過采樣便可完成對其的卷積處理，以非下采樣雙通道濾波器為處理對象，完成對其插值處理，具有以下精確重構(gòu)條件：

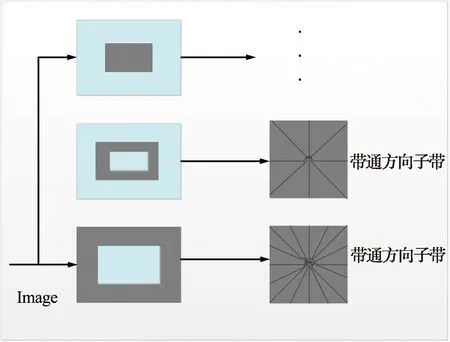
(a)NSCT

(b)Lena圖進行2層NSCT圖2 NSCT和Lena圖進行2層NSCTFig.2 NSCT and Lena diagram of two layers NSCT

H0(w)G0(w)+H1(w)G1(w)=1。

(5)

其次，為非采樣方向濾波器組(Non-subsampled Directional Filter Bank,NSDFB)，該部分能夠?qū)D像展開多尺度分析，并移除低頻帶通部分，只對高頻帶通展開方向分析。在以上2部分的共同作用下，使NSCT具有多尺度分析性、多方向性以及平移不變性等優(yōu)勢。

以Lena圖像為處理對象，完成對其的NSCT處理，如圖2(b)所示。可以看出，與原始圖像相比，所獲取的帶通子帶圖像與其具有相同的尺寸[8]。

1.4 QR碼

QR碼是目前使用廣泛，通過掃碼可以獲得大量數(shù)據(jù)信息的載體，數(shù)據(jù)信息包含數(shù)字、漢字等不同數(shù)據(jù)類型。二維碼屬于矩陣式二維條碼，以二進制進行存檔，其中黑用二進制“1”表示，白用二進制“0”表示，QR碼的主要部分包括功能區(qū)和編碼區(qū)，如圖3所示。

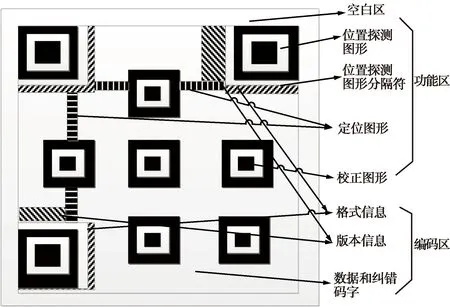
圖3 QR碼結(jié)構(gòu)Fig.3 QR code structure

原始水印包含的信息為“飛行學(xué)院”，如圖4(a)所示，借助QR碼來完成對圖4(a)水印信息編碼，生成QR碼水印，如圖4(b)所示。

(a)原水印

(b)QR碼水印圖4 原水印圖像和QR碼的水印圖像Fig.4 Original watermark image and QR code watermark image

2 QR碼雙重加密復(fù)合數(shù)字水印算法

本文算法原理如圖5所示。

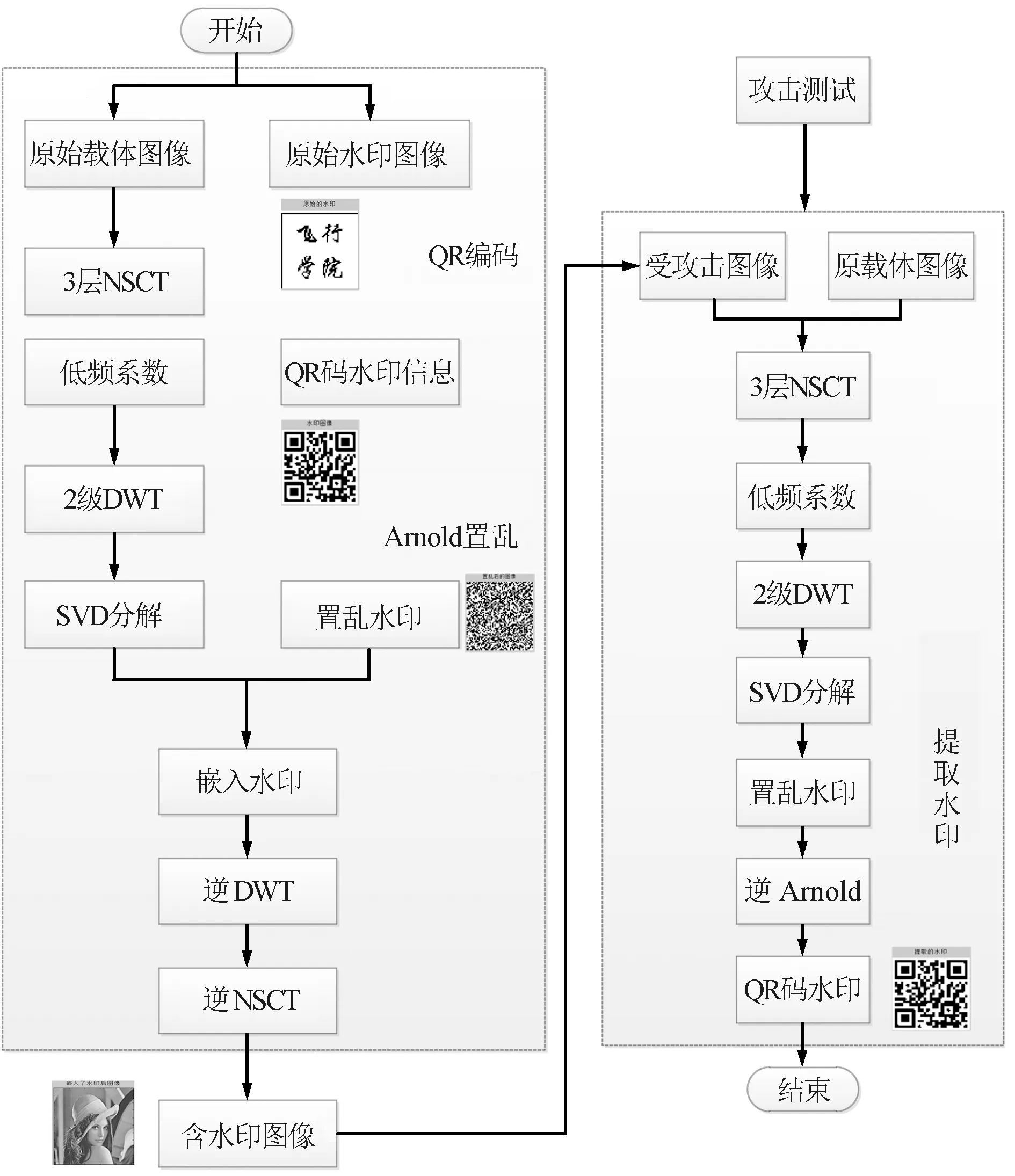
圖5 算法原理Fig.5 Watermark embedding process

對于一個優(yōu)秀的水印算法，在載體圖像中完成對水印信息的嵌入時，需實現(xiàn)對圖像加入版權(quán)信息失真問題的有效控制，在滿足算法隱蔽性的前提下，確保版權(quán)加入后的信息能夠?qū)Ω黝惞暨M行抵抗，并具有極為出色的魯棒性，保障對“云”端環(huán)境下圖像安全保護。NSCT在該算法中發(fā)揮著重要作用，可借助其高冗余性實現(xiàn)對大量信息的嵌入，完成對低頻部分的分解之后，出錯的邊緣輪廓信息便會被集中在該部分之中，即便其發(fā)生變化，依然不會因處理而對信息有較大的影響。

2.1 水印嵌入過程

首先，對“飛行學(xué)院”的水印信息通過編碼轉(zhuǎn)換成QR編碼的水印信息，為了確保水印的安全性，再將QR碼的水印信息進行Arnold變換置亂再次進行加密。原始載體Lena圖像首先進行3層NSCT，選擇儲存信息更多的低頻部分進行DWT，然后對圖像抵抗力較強的低頻圖像進行SVD，對奇異值加權(quán)疊加與SVD的酉矩陣重構(gòu)低頻圖像，連同高頻各部分執(zhí)行小波逆變換，與各系數(shù)進行逆NSCT，將水印信息嵌入到載體圖像中。

與原圖像相比，變換后的圖像與其大小相同，借助對低頻的處理，使嵌入的信息量增多，在嵌入強度滿足相關(guān)標準的前提下，水印加權(quán)重構(gòu)低頻，統(tǒng)一完成對各個系數(shù)的小波反變換處理，同時對其展開逆NSCT，對水印圖像進行獲取。此多重算法強化了抵抗幾何攻擊的能力，具體實現(xiàn)步驟如下：

① 對水印信息進行讀取，包含的內(nèi)容為“飛行學(xué)院”，然后完成對其的QR編碼，從而實現(xiàn)對QR水印圖像的獲取，使信息具有較高的安全性，借助Arnold變換來完成對水印信息的置亂以及加密處理；

② 對載體圖像進行3層NSCT，變換后選擇儲存信息更多的低頻部分進行2級DWT；

③ 借助小波分解后的低頻展開SVD處理如下:A=USVT，處理后獲得奇異值區(qū)間，即S=[λ1λ2…λt]；

④ 對嵌入強度進行確定，在完成了對水印信息的分解處理后，需在奇異值矩陣上完成對其的分解處理，從而可得S′=S+αW；

⑥ 完成了對低頻部分的重構(gòu)后，通過對其的逆DWT來完成對系數(shù)的重構(gòu)，然后通過逆NSCT來對水印圖像進行獲取。

2.2 水印提取過程

水印嵌入流程的逆過程可用來對水印進行提取，具體步驟如下：

① 對原載體圖像和已嵌入水印的圖像分別進行3層NSCT，獲取低頻子帶矩陣進行2級小波變換；

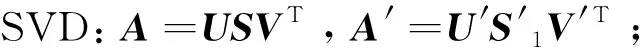
③ 完成對奇異值矩陣以及水印奇異值的獲取后，將二者做差處理；

⑤ 完成對水印圖像的獲取后，對其進行解密處理。

3 仿真實驗

本文在水印透明性和魯棒性2方面對算法進行評估，水印隱蔽性及視覺效果通過峰值信噪比 (Peak Signal to Noise Ratio，PSNR)作為衡量標準，計算如式(6)所示，水印的魯棒性通過用相似度 (Normalized Cross-correlation，NC)作為評判標準，計算如式(7)所示。

(6)

(7)

式中，A代表原始載體圖像，通過嵌入算法進行水印嵌入；B代表圖像；a代表原始水印圖像，通過提取算法提取水印；b代表水印。對于隱蔽性以及PSNR值來說，二者存在正比關(guān)系，算法的不可見性會隨其值的不斷增大而變好。NC的取值為0～1，其與魯棒性存在著正比關(guān)系，當其趨近于1時，則表示該算法具有良好的穩(wěn)定性。

3.1 水印透明性測試

實驗所選用的原始載體圖像由Lena，Baboon，Barbara，Peppers以及Gameraman等圖像組成，其分辨率均為512 pixel×512 pixel，水印圖像由實用性較強的QR碼水印圖像充當，其是由64×64“飛行學(xué)院”信息編碼而成，選用‘pkva’和‘maxflat’作為基函數(shù)來完成NSCT，原始載體以及嵌入水印后等圖像如圖6所示。

(a)Lena嵌入水印前、后的圖像

(b)Baboon 嵌入水印前、后的圖像

(c)Gameraman 嵌入水印前、后的圖像

(d)Barbara 嵌入水印前、后的圖像

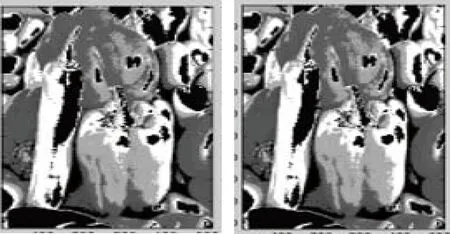
(e)Peppers 嵌入水印前、后的圖像圖6 嵌入水印前、后的圖像Fig.6 Watermark image before embedding and embedded watermark image

經(jīng)實驗得到峰值計算結(jié)果，載體Lena圖像的PSNR值為32.631 4 dB，載體Barbara圖像的PSNR值為33.852 5 dB，載體Gameraman圖像的PSNR值為33.826 5 dB，載體Peppers圖像的PSNR值為33.831 4 dB，載體Baboon圖像的PSNR值為33.735 2 dB，PSNR值均大于20 dB。在不同的圖像中進行算法實驗，可以看出，5幅原始載體圖像與嵌入水印后的圖像在視覺上看不出任何差異，證明本文算法滿足水印隱蔽性測試需求，達到了較好的視覺效果。

3.2 水印安全及魯棒性測試

原水印和提取的水印圖像如圖7所示。

(a)原水印圖像

(b)QR碼水印

(c)置亂的水印圖像

(d)提取的水印圖像圖7 原水印和提取的水印圖像Fig.7 Original watermark and extracted watermark image

實驗將“飛行學(xué)院”組成的原水印圖像經(jīng)QR碼提取得到QR碼水印圖像，同時為了對安全性起到更深層的防護，將QR碼水印圖像再次進行Arnold置亂加密，得到置亂的水印圖像，將置亂的水印圖像通過提取算法提取水印圖像得到提取的水印圖像。由圖7(d)和圖7(b)可以看出，2幅圖幾乎一樣，說明算法魯棒性較好，5幅圖像通過式(7)計算的NC值如表1所示，均為1.000 0。

表1 未攻擊的性能指標Tab.1 Unattacked performance metrics

以本算法為研究對象，為了完成對其魯棒性的測試，本文對其展開了一系列抗攻擊測試，在完成了對Lena含水印圖像的攻擊之后，對相應(yīng)的水印圖像進行提取，如圖8所示。由圖8可以看出，可對較清晰的水印圖像進行提取，即能夠輕易實現(xiàn)對圖像信息的識別。

(a)椒鹽噪聲

(b)高斯噪聲

(c)剪切

(d)JPEG壓縮

(e)旋轉(zhuǎn)

(f)高斯濾波

(g)中值濾波

(h)椒鹽濾波圖8 含水印圖像受椒鹽噪聲、高斯噪聲、剪切、JPEG壓縮及旋轉(zhuǎn)和高斯濾波攻擊后的圖像Fig.8 Images after watermarked images attacked by salt and pepper noise, Gaussian noise, cut, JPEG compression and rotation, and Gaussian filtering

算法對5幅含水印圖像均進行相同的攻擊，計算得到的NC值如表2所示。

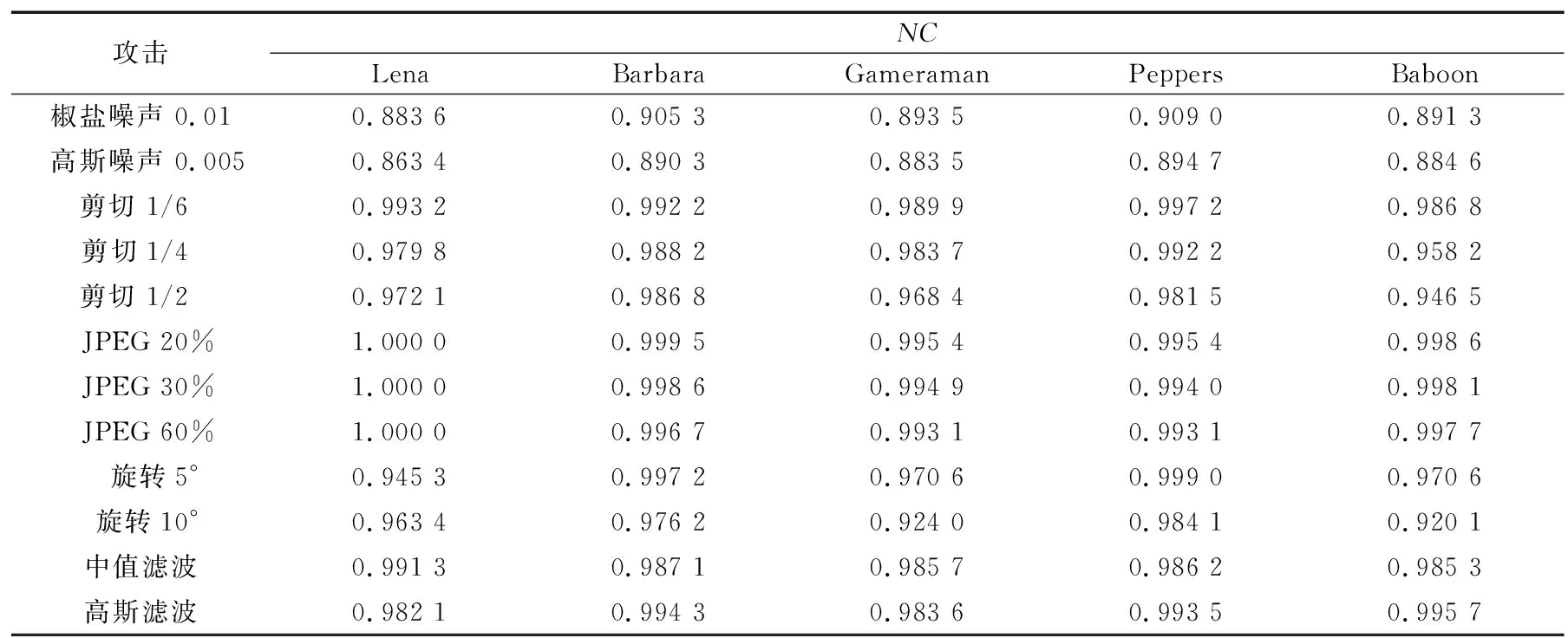
表2 本文算法魯棒性測試Tab.2 Algorithm robustness test

可以看出，本文算法抵抗攻擊的能力較強，尤其對剪切、壓縮、旋轉(zhuǎn)和濾波攻擊，都表現(xiàn)出了較好的魯棒性，NC值都在0.94以上。

3.3 算法比較

與其他算法相比，本文算法有諸多優(yōu)勢。與文獻[10,18]所提出的相關(guān)算法相比，文獻[10]對DWT-SVD以及QR進行了綜合運用，文獻[18]則實現(xiàn)了對SVD，NSCT以及DCT等的有效融合，本文所研究的水印圖像中含有QR編碼，由其來充當水印信息，然后通過Arnold完成對水印的置亂，從而使算法具有較高的透明性以及安全性，實現(xiàn)了對SVD，NSCT以及DCT等的有效融合，在對各類攻擊的抵抗方面，具有更高的穩(wěn)定性。具體的測試比較如表3所示。

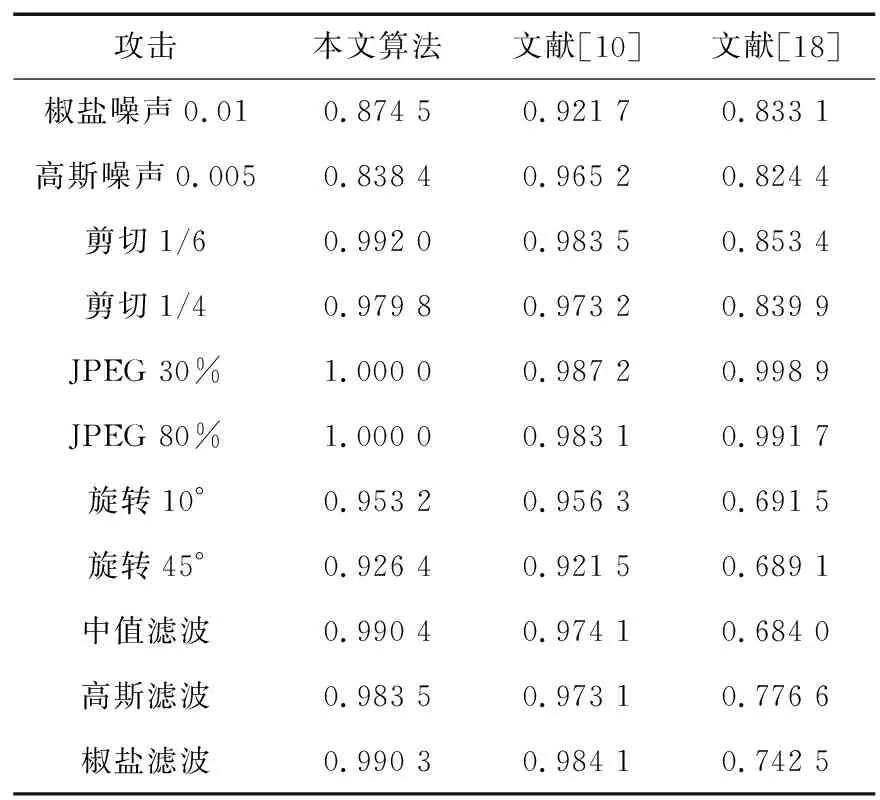
表3 本文算法與文獻[10，18]算法攻擊測試比較Tab.3 Comparison of proposed algorithm and Literature[10，18] algorithm attack test

4 結(jié)束語

“云”端環(huán)境下，為避免數(shù)字圖像信息共享遭受侵權(quán)行為，以水印信息為研究對象，為了使其安全性得到提升，完成對Arnold置亂以及QR碼的有效結(jié)合，以雙重加密為理論依據(jù)，提出了相應(yīng)的水印算法，該算法對SVD，NSCT以及DWT等進行了綜合運用，在復(fù)合數(shù)字水印算法中引入了雙重加密算法，以“云”端普遍使用的QR碼為理論基礎(chǔ)，提出一種NSCT-DWT-SVD雙重加密復(fù)合數(shù)字水印算法，聯(lián)合變換為該算法的核心內(nèi)容，能夠?qū)Υ罅啃畔⑦M行嵌入，具有極強的穩(wěn)定性，可將算法運用在多圖像之中，并展開相關(guān)測試，不僅能夠成功完成透明性測試，同時在對各類攻擊的抵抗方面，其穩(wěn)定性得到了大幅度提升。不同于文獻[10,18]，本文算法在面對濾波、剪切、旋轉(zhuǎn)以及壓縮等攻擊時均表現(xiàn)出較強勁的魯棒性，在“云”端環(huán)境下有較好的應(yīng)用保護價值。