洪水波周期性對(duì)堤防穩(wěn)定性影響的數(shù)值模擬

楊 菁

(南昌市城市防洪事務(wù)中心，江西 南昌 330000)

1 研究方法

1.1 靈敏度分析

本文應(yīng)用靈敏度分析方法確定對(duì)堤防狀態(tài)影響最大的洪水波參數(shù)。分析可分為三個(gè)階段，分別計(jì)算靈敏度比、靈敏度評(píng)分和總相對(duì)靈敏度。

靈敏度比ηSR可以描述為模型輸出的百分比變化除以輸入變量的單位變化，如式(1)：

(1)

式中：f(xL,G)為利用給定輸入?yún)?shù)xL,G的變化值后得到的輸出變量值；f(xm)為利用給定參數(shù)的參考值xm后得到的模型輸出參考值。

對(duì)于每一個(gè)考慮的參數(shù)，本文計(jì)算了四個(gè)靈敏度比。可以分為兩類：局部和全局。對(duì)于局部類別，輸入?yún)?shù)值xL在隨機(jī)集的一個(gè)小區(qū)間內(nèi)變化。在全局靈敏度比中，給定參數(shù)xG的輸入值在隨機(jī)集的整個(gè)范圍內(nèi)變化(如圖1)。

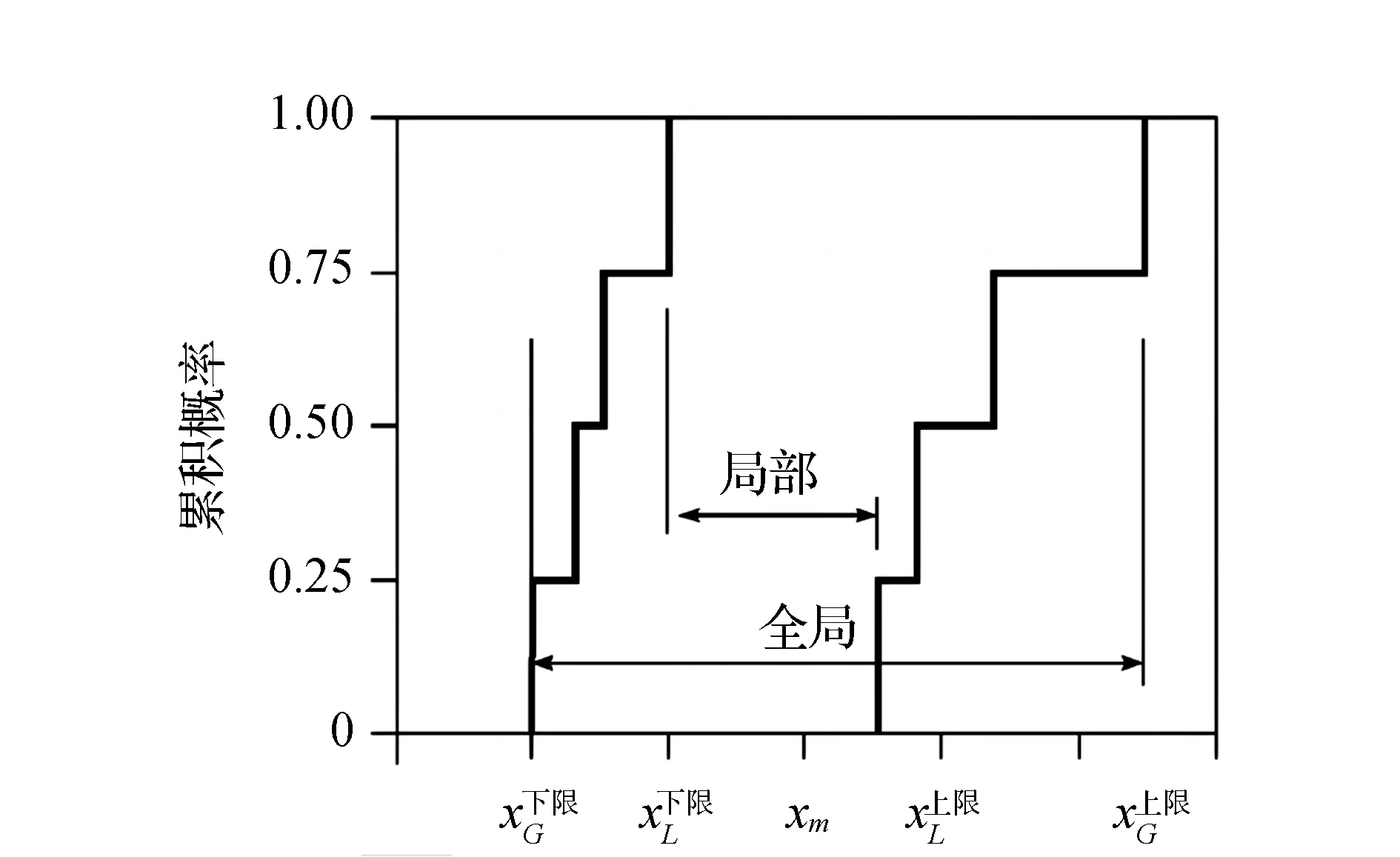
圖1 局部和全局范圍區(qū)間的靈敏度比圖示

靈敏度評(píng)分ηSS是評(píng)估給定模型不確定性的一種方法，可以通過對(duì)輸入?yún)?shù)中的靈敏度比值進(jìn)行歸一化和加權(quán)來獲得。如式(2)：

(2)

歸一化過程使靈敏度評(píng)分獨(dú)立于給定參數(shù)的輸入值單位。靈敏度評(píng)分ηSS,i(i=1,2,…,N)是針對(duì)考慮的所有N個(gè)基本參數(shù)計(jì)算的。

每個(gè)輸入變量的總相對(duì)靈敏度α(xi)計(jì)算為每個(gè)輸入?yún)?shù)ηSS,i在位移、力、孔隙壓力或安全系數(shù)等相應(yīng)結(jié)果上所有靈敏度評(píng)分(局部和全局范圍)的總和。可以寫為公式(3)：

(3)

一旦確定閾值，總相對(duì)靈敏度可用于確定哪些參數(shù)對(duì)安全系數(shù)有顯著影響。通常認(rèn)為5%～10%的閾值是合適的。

1.2 洪水波周期性建模

利用二維顯式有限差分軟件FLAC[1-7]對(duì)洪水路堤狀態(tài)的影響進(jìn)行了數(shù)值模擬。該軟件允許執(zhí)行機(jī)械—流體和流—熱耦合過程用于堤防穩(wěn)定性建模。

(1)地質(zhì)模型描述。本文對(duì)建造的實(shí)驗(yàn)路堤進(jìn)行數(shù)值計(jì)算。與實(shí)驗(yàn)路堤橫截面一致的假定數(shù)值模型幾何結(jié)構(gòu)如圖2所示。假設(shè)模型的材料參數(shù)如表1所示。

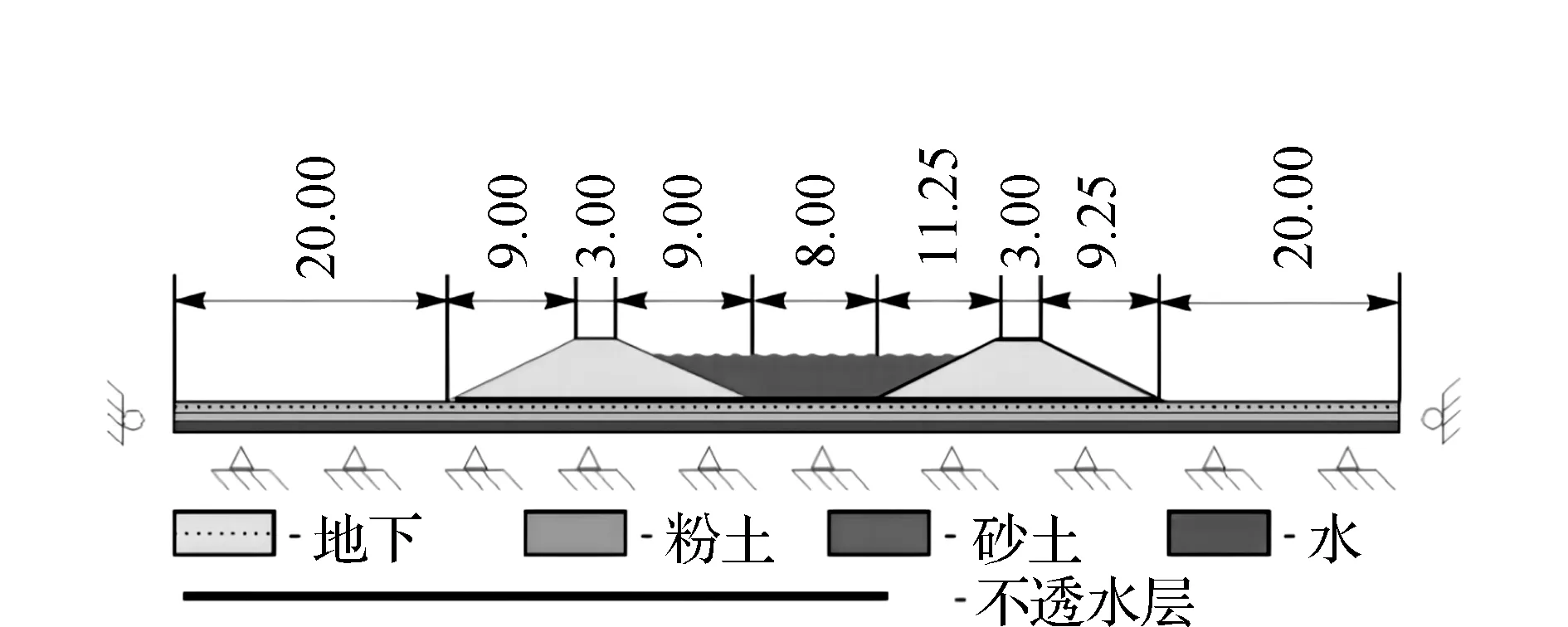
圖2 用于數(shù)值計(jì)算的地質(zhì)模型幾何結(jié)構(gòu)(單位：m)

表1 材料參數(shù)

(2)洪水過程靈敏度分析說明。在靈敏度分析中，研究了兩種類型的洪水過程：?jiǎn)未魏樗ê碗p次連續(xù)洪水波。兩個(gè)參數(shù)區(qū)間是獨(dú)立確定的。第一組是通過對(duì)研究流域歷史洪水的分析確定的。第二組是在已有經(jīng)驗(yàn)和文獻(xiàn)研究[8-9]的基礎(chǔ)上對(duì)水位變化速率和水位高度應(yīng)用了某些限制值。

(3)數(shù)值計(jì)算。對(duì)于上述洪水過程的靈敏度分析，需要21個(gè)確定性模型。在每個(gè)模型中，采用每個(gè)參數(shù)局部和全部范圍區(qū)間的下限或上限。其余4個(gè)參數(shù)的值用參考值固定。數(shù)值模擬的結(jié)果為假定數(shù)值模型中每個(gè)計(jì)算節(jié)點(diǎn)上的孔隙壓力分布和垂直位移。對(duì)所有21個(gè)洪水過程開發(fā)情景的值進(jìn)行處理，以確定5個(gè)基本參數(shù)中哪一個(gè)最重要，對(duì)輸出變化影響最大。

2 洪水波參數(shù)靈敏度分析結(jié)果

對(duì)堤壩上單次洪水波和雙連續(xù)洪水波進(jìn)行了洪水波參數(shù)靈敏度分析。圖3～圖9顯示了所有計(jì)算節(jié)點(diǎn)的分析結(jié)果，表明了基本洪水波參數(shù)對(duì)路堤內(nèi)孔隙壓力分布和垂直位移的影響。這些曲線圖對(duì)應(yīng)于上述靈敏度評(píng)分值(見式(2))，還給出了與總相對(duì)靈敏度(見式(3))相對(duì)應(yīng)的孔隙壓力分布和垂直位移的靈敏度分析結(jié)果。在曲線圖中，靈敏度評(píng)分和總相對(duì)靈敏度值小于10%。

2.1 單次洪水波后的靈敏度結(jié)果

對(duì)21種情景進(jìn)行了不同持續(xù)時(shí)間的洪水過程數(shù)值模擬。洪水波模型的持續(xù)時(shí)間從9～14 d不等。使用孔隙壓力和垂直位移分布的靈敏度評(píng)分以及總相對(duì)靈敏度進(jìn)行靈敏度分析，結(jié)果分別如圖3～圖5所示。

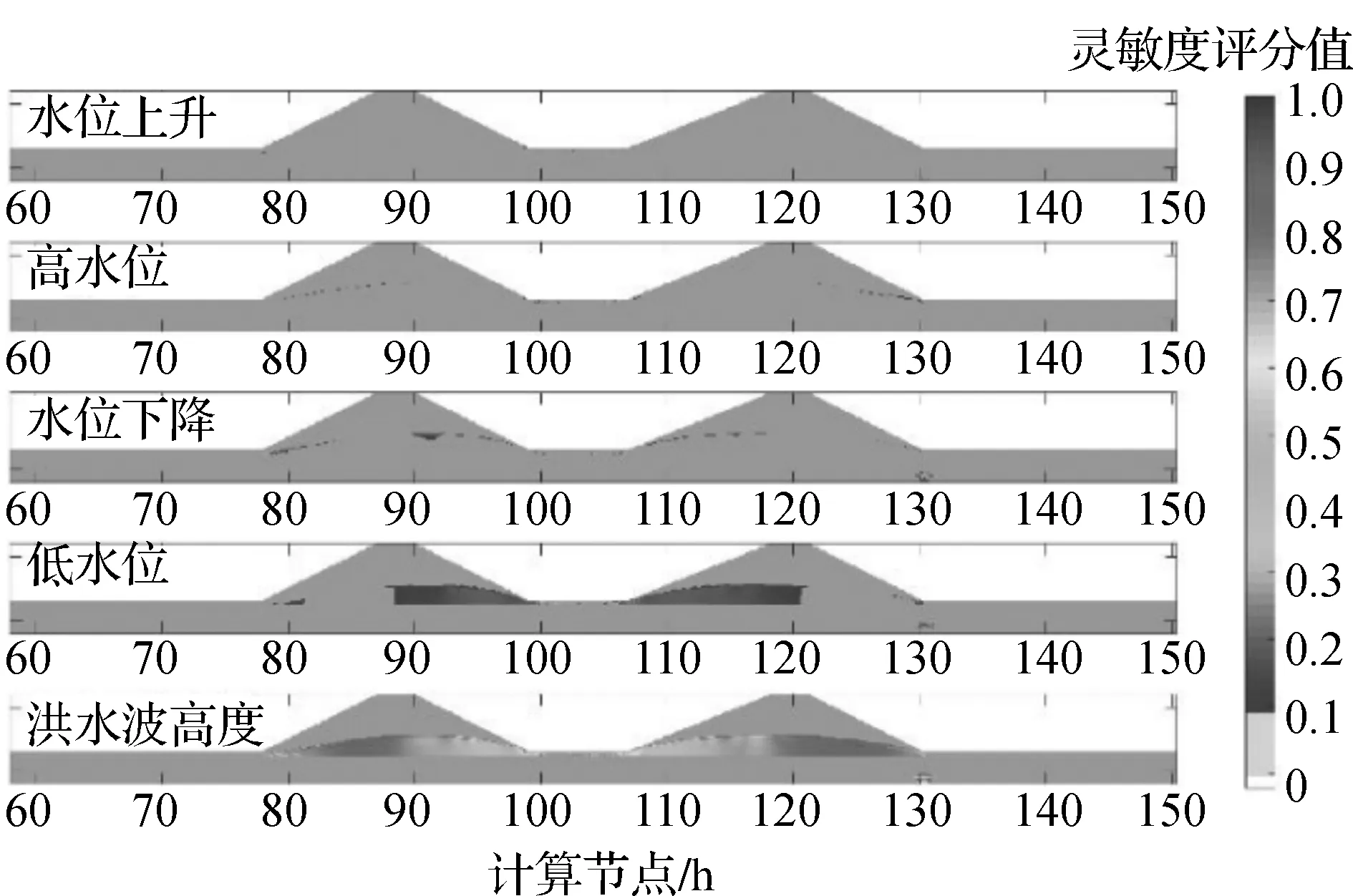
圖3 單次洪水波參數(shù)對(duì)孔隙壓力分布的靈敏度評(píng)分值

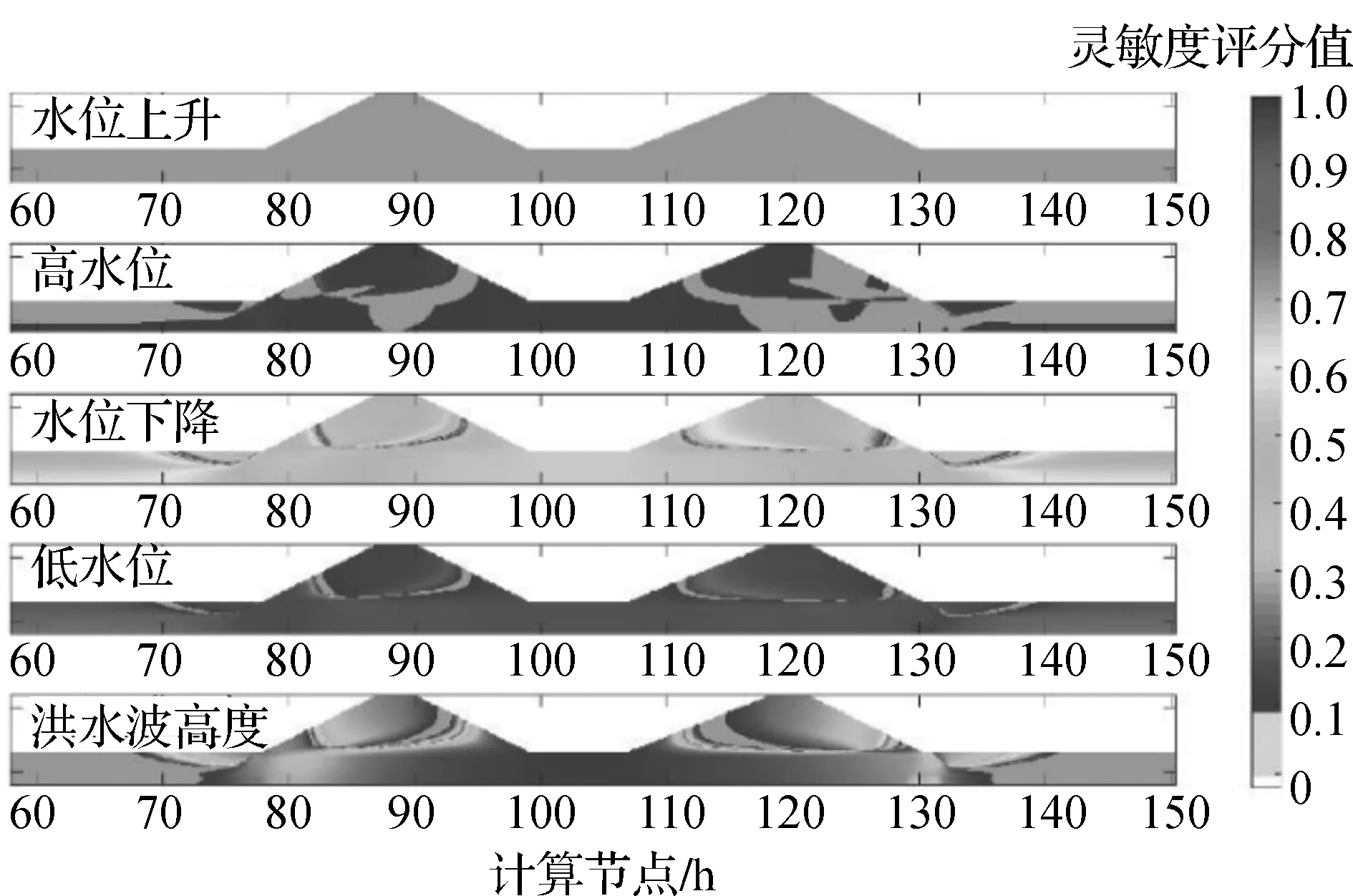
圖4 單次洪水波參數(shù)對(duì)垂直位移分布的靈敏度評(píng)分值

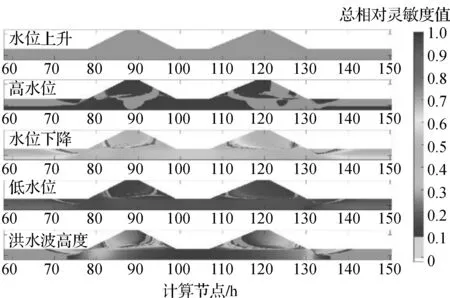
圖5 單次洪水波參數(shù)的總相對(duì)靈敏度值

對(duì)孔隙壓力場(chǎng)和垂直位移建模以獲得靈敏度評(píng)分值分布，可以觀察到水位上升速率對(duì)其沒有影響。這也反映總相對(duì)靈敏度值實(shí)際上<5%。孔隙壓力模擬結(jié)果的靈敏度評(píng)分表明，影響最顯著的洪水波參數(shù)是連續(xù)洪水波后的水位和時(shí)間間隔。但在一些路堤區(qū)域，水位下降速率和持續(xù)時(shí)間也是顯著值。對(duì)堤防垂直位移進(jìn)行了相同計(jì)算，結(jié)果表明，可以觀察到水位下降速率和持續(xù)時(shí)間影響的區(qū)域。圖5顯示，當(dāng)接受10%的閾值時(shí)，堤防穩(wěn)定性分析中有四個(gè)最重要的參數(shù)，即高水位持續(xù)時(shí)間、高水位下降速率、連續(xù)洪水波之間的時(shí)間間隔和水位。

2.2 雙連續(xù)洪水波后的靈敏度結(jié)果

將洪水波參數(shù)靈敏度分析的研究擴(kuò)展到雙洪水波的情況。這種分析能夠估計(jì)低水位持續(xù)時(shí)間參數(shù)對(duì)路堤內(nèi)孔隙壓力和垂直位移值分布的實(shí)際影響。與單次洪水過程的情況一樣，不同的洪水波模擬持續(xù)時(shí)間適用于所有21種情景。在這種情況下，洪水過程的最短情景時(shí)間為18 d，而最長(zhǎng)情景時(shí)間為28 d。圖6～圖8分別給出了使用孔隙壓力和垂直分布的靈敏度評(píng)分以及雙洪水波周期的總相對(duì)靈敏度分析結(jié)果。

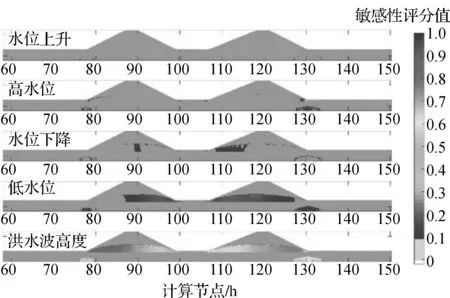
圖6 雙連續(xù)洪水波參數(shù)對(duì)孔隙壓力分布的敏感性評(píng)分值

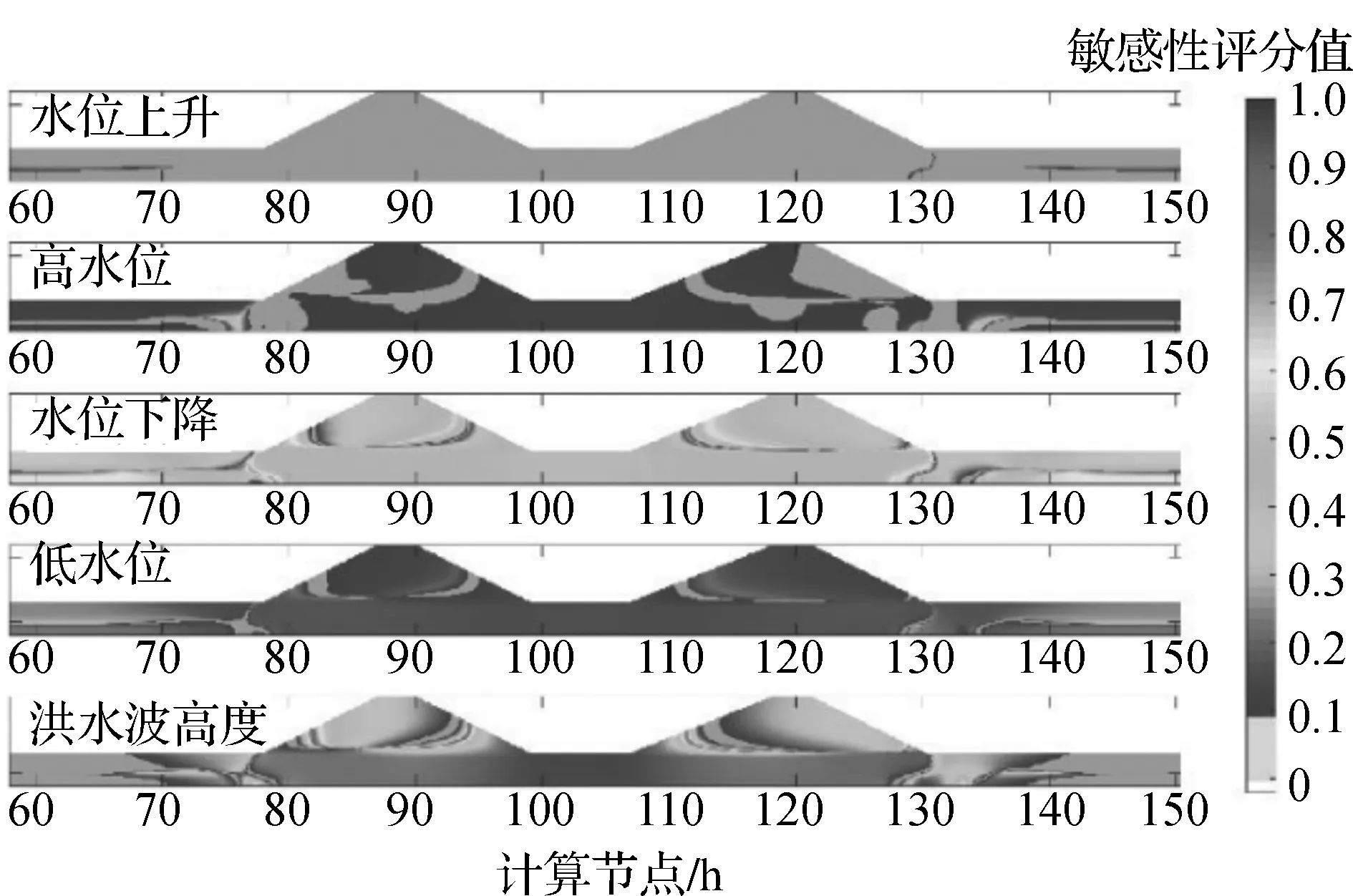
圖7 雙連續(xù)洪水波參數(shù)對(duì)垂直位移分布的敏感性評(píng)分值

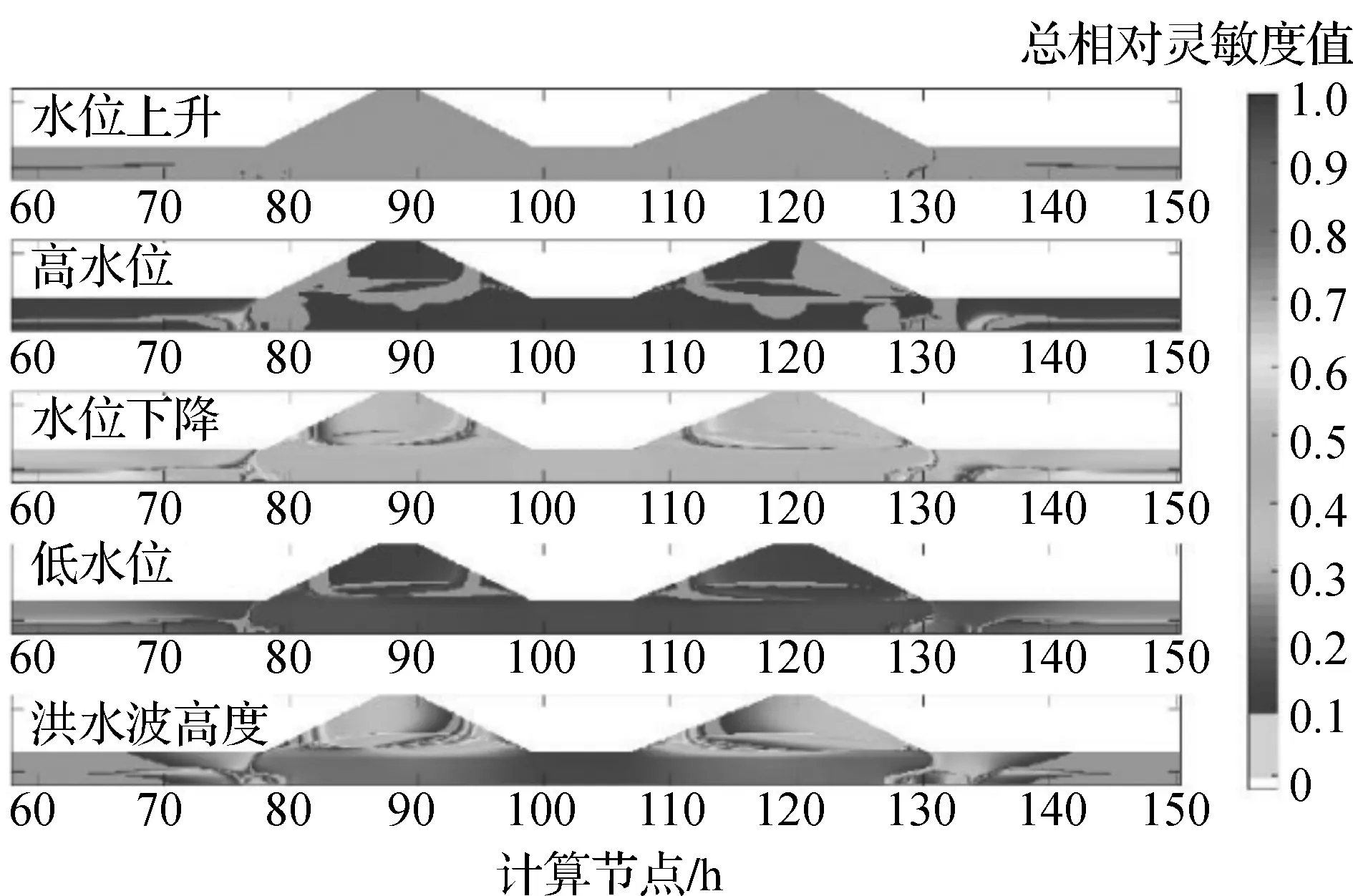
圖8 雙連續(xù)洪水波參數(shù)的總相對(duì)靈敏度值

靈敏度分析在雙連續(xù)洪水波模型中的應(yīng)用結(jié)果也表明，水位上升速率對(duì)堤防狀態(tài)影響不顯著。其值是固定的，不應(yīng)包括在洪水波情景的確定中。雙連續(xù)洪水波影響的靈敏度分析表明，水位下降速率和高水位持續(xù)時(shí)間對(duì)孔隙壓力結(jié)果的影響大于單次洪水波的計(jì)算結(jié)果。這是第一次洪水波造成的現(xiàn)有飽和度的結(jié)果。圖9顯示了單次洪水波和雙連續(xù)洪水波計(jì)算的總相對(duì)靈敏度值之間的差異。

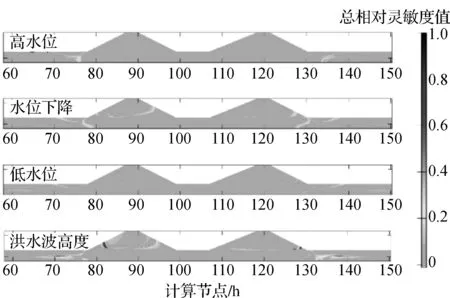
圖9 單次洪水波和雙連續(xù)洪水波總相對(duì)靈敏度值的差異

差值圖表明，四個(gè)參數(shù)對(duì)剩余飽和度都很敏感。兩種情景下差異的位置通常在路堤的同一部分。在所有四個(gè)重要的洪水過程參數(shù)中，水位曲線圖達(dá)到最高值。相對(duì)于其他參數(shù)來說，在路堤的最大面積上計(jì)算出的單次洪水波和雙連續(xù)洪水波的水位總相對(duì)靈敏度值差異也很明顯。

3 結(jié) 論

(1)靈敏度分析方法對(duì)于檢測(cè)對(duì)垂直位移和孔隙壓力分布影響最大的路堤位置非常實(shí)用。

(2)對(duì)單次洪水波情景和雙連續(xù)洪水波進(jìn)行靈敏度分析，得出了關(guān)于洪水波參數(shù)重要性的相同結(jié)論。兩種類型的情景(單次洪水波、雙連續(xù)洪水波)都表明水位上升速率對(duì)堤防狀態(tài)影響不顯著。確定了對(duì)堤防狀態(tài)影響最大的洪水波四個(gè)重要參數(shù)為高水位持續(xù)時(shí)間、高水位下降速率、連續(xù)洪水波之間的時(shí)間間隔和水位。

(3)靈敏度分析檢測(cè)了總相對(duì)敏感度值的最大差異，得出兩種情景下差異的位置通常在路堤的同一部分，即為路堤內(nèi)最易受到連續(xù)洪水波影響的區(qū)域。