大跨度體育館風效應的大渦模擬及風洞試驗的對比研究

郅倫海, 程 磊, 孟 磊, 劉毛方

(1.合肥工業大學 土木與水利工程學院,安徽 合肥 230009; 2.安徽省金田建筑設計咨詢有限責任公司,安徽 合肥 231600)

因為大跨度屋蓋結構的自重輕、阻尼小、柔度大,自振周期與風速的卓越周期接近[1],通常位于大氣邊界層中風速變化大、湍流度高的近地區域,主要受到氣流的分離和再附流作用[2],所以大跨度屋蓋結構對風荷載極其敏感。大跨度屋蓋結構的風荷載特性不僅與結構造型有關,還與所處的建筑環境有關。周邊群體建筑分布愈加密集,大跨度屋蓋結構受到的遮擋效應和狹縫效應會愈加顯著[3]。現場實測和風洞試驗數據顯示,在大跨度屋蓋迎風前端,氣流分離現象嚴重,脈動風壓極值會達到平均風壓的3.5倍以上[4],其影響十分嚴重。因此有必要開展群體布局下大跨度屋蓋結構平均風壓及脈動風壓的研究。

本文以合肥某大跨度體育館為工程背景,利用計算流體動力學軟件Fluent,采用大渦模擬(large eddy simulation,LES)湍流模型,基于隨機湍流生成法得到入口脈動風速,對體育館主副兩館進行風荷載模擬,計算并分析主館表面的平均風壓系數及脈動風壓系數分布特性,并將計算結果與風洞動態測壓試驗進行對比。結果表明數值模擬較好地反映了群體布局下主館表面風壓分布特性,得到的風壓系數與風洞試驗數據有較好的吻合。本文方法和研究結果對于確定群體布局下,復雜體型的大跨屋蓋結構屋面的風荷載具有一定的工程意義和科學價值。

1 工程概況

該大跨體育館由主館和副館組成,如圖1所示。副館南北方向跨度為52.0 m,東西方向跨度為103.5 m,屋蓋側立面由四邊形與三角形構成,屋面由傾斜的四邊形屋面板拼接而成,相鄰屋面板空隙處由三角形屋面板封閉,屋面最高點標高為29.0 m,最低點標高為23.5 m;主館南北方向跨度為130.5 m,東西方向跨度為103.5 m,屋蓋構造與副館相同,屋面標高為35.0 m。主館與副館之間水平最短距離為10.0 m。體育館東面無遮擋,北面、西面、南面存在較多高低層建筑,其中最高建筑高達75.0 m。合肥市50 a重現期基本風速為 27.1 m/s,按 C類地貌考慮。

圖1 建筑效果圖

2 大渦模擬數值風洞計算

2.1 控制方程

大渦模擬采用空間過濾方法,分離湍流流場中的大尺度渦和小尺度渦;對大尺度渦,采用直接模擬直接計算;對小尺度渦,采用亞格子模型來模擬其對流場的影響。過濾后的連續性方程和Navier-Stokes方程式如下:

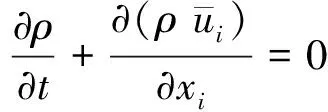
(1)

(2)

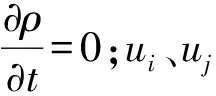
2.2 計算模型及網格劃分

數值風洞計算幾何建模時按1∶1實際尺寸建模,考慮周圍900 m內建筑群,建立體育館群體模型,幾何模型如圖2所示。文獻[5]表明,當計算域阻塞率小于3%時,可以忽略計算域邊界對建筑表面風壓分布的影響,阻塞率ω計算公式為:

圖2 體育館群體模型

ω=(A0/A1)×100%

(3)

其中:A0為建筑物最大的迎風面積;A1為計算域界面的面積。

基于以上要求,并考慮數值模擬準確性和模擬計算成本,經多次試算后,確定計算域尺寸為x×y×z=2 000 m×3 500 m×300 m,經過計算,最大阻塞率為0.6%,滿足要求。為提高計算效率,將整個計算域分成2個部分:一部分為外圍區域,其形狀規整;另一部分為核心區域,包含體育館模型及周邊建筑,如圖3所示(單位為m)。模擬不同風向角來風工況時,將外圍區域旋轉相應角度,即可建立該工況下數值模型。針對不同風向角工況,分別進行網格劃分。

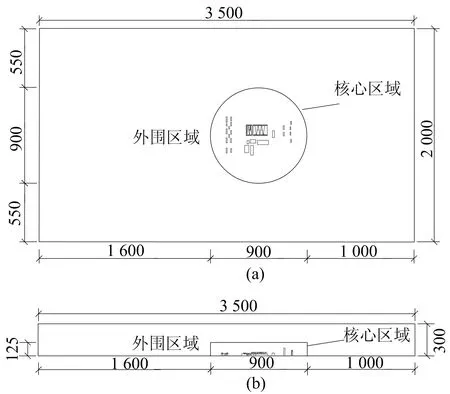
圖3 計算域示意圖

由于該大跨度體育館造型復雜,特別是屋面凸起部分存在尖角,難以在計算域中生成高質量六面體結構化網格。為正確模擬大氣邊界層的風場特性,獲得氣流撞擊復雜造型屋蓋后的流動現象;劃分高質量網格,提高計算效率;故在Fluent Meshing中,采用多面體網格對整個計算域進行網格劃分。在網格劃分前,先在建模軟件Space Claim中將核心區域與外圍區域的交界面、交界線共享拓撲,使2個計算域的交界面、交界線在網格劃分時共節點,提高數據傳遞效率和計算收斂性,交界面在Fluent中自動識別為internal。外圍區域形狀規整,采用較大尺度網格進行劃分,面網格尺寸為1～20 m;核心區域形狀復雜,采用較小尺度網格進行劃分,裙房面網格為1～5 m,各風向下,體育館表面網格最小尺寸為0.05 m,最大尺寸為0.30 m。總體網格數量為6×106左右。在體育館表面生成3層貼體棱柱體網格,第1層壁面網格高度取0.001 m,網格尺寸增長率為1.2,最大網格歪斜度為0.75。文獻[6]證明了高雷諾數瑞流下LES壁面函數對近壁面處理的正確性。本文體育館近壁面y+值為3.5～95.0，在對數率區域內,使用壁面函數對近壁面進行處理,使近壁面滿足LES湍流模型的要求,保證模擬結果的準確性。

2.3 邊界條件

入口邊界采用速度入口(velocity-inlet)。根據文獻[7],大氣邊界層內風速隨高度變化規律采用指數律風剖面來描述,即

vz=v0(z/z0)α

(4)

其中:vz為任意高度z處的平均風速;v0為標準高度處的平均風速;z為建筑物計算位置離地面的高度;z0為標準高度,取10 m;α為地面粗糙度指數,在C類地貌條件下,取值為0.22。

通過湍動能k和湍流耗散率ε來確定入口處湍流邊界條件,由等效邊界層假設[1]給出表達式,即

k(z)=1.2[I(z)vz]2

(5)

(6)

其中:Cμ為模型常數,取值為0.09;K為卡門常數,取值為0.4;I、Lu分別為湍流強度和湍流積分尺度。參考文獻[8],I、Lu的計算公式分別為:

(7)

Lu=100(z/30)0.5

(8)

其中:zb=5 m;zB=350 m。

入口湍流通過Spectral Synthesizer[9-10]方法生成,由于計算域出口距離建筑物足夠遠,可認為出口處尾流已充分發展,出口邊界采用自由出流邊界(outflow),流場變量散度為0;計算域的頂面和側面采用對稱邊界(symmetry),在Fluent中對稱邊界即無壁面剪應力的自由滑移壁面;地面和建筑物表面采用壁面條件(wall),為無滑移光滑壁面。

2.4 求解參數設置

在數值求解中,認為空氣是不可壓縮流體。采用WMLES亞格子模型對N-S方程進行求解,計算離散方程組采用分離式解法中的SIMPLEC算法來求解。為保證數值離散精度,動量方程中的對流項采用數值耗散低的二階中心差分格式,時間項采用二階隱式格式。為加快數值模擬計算收斂,在進行非定常大渦模擬計算前,先采用RANS模型進行定常計算,并把計算結果瞬態化處理,作為LES的初始流場。LES計算的時間步長取0.05 s,相當于20 Hz的采樣頻率,能正確反映實際脈動風壓特性,共進行10 000步的LES非定常計算。

3 數值模擬結果分析

大跨度體育館為封閉結構,結構表面某i點的風壓系數計算公式為:

(9)

結構表面點i處的平均風壓系數的計算公式為:

(10)

同時由(9)式、(10)式可得,結構表面點i的脈動風壓系數均方根為:

(11)

其中:Cpi(t)為試驗模型上第i個測壓孔所在位置的風壓系數;pi(t)為該位置上測得的表面風壓值;p0、p∞分別為參考點處測得的平均總壓和平均靜壓,參考點高度取45 m處;tm為某一時刻;N為時域點數。

模擬時將正北方向定義為0°風向,逆時針旋轉,每隔15°為一個試驗工況,共24個試驗工況，如圖4所示。限于篇幅,本文僅給出0°風向角工況下數值模擬結果。

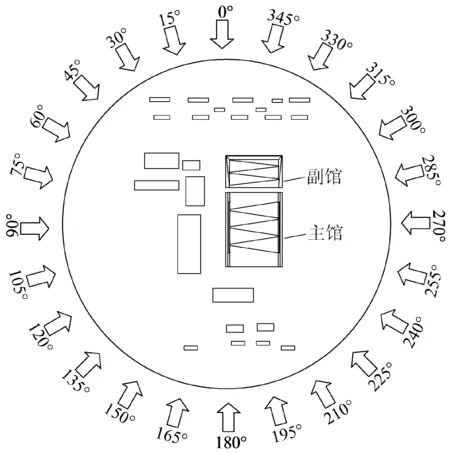
圖4 風向角示意圖

3.1 平均風壓系數

主館表面平均風壓系數分布如圖5所示。經仔細研究0°風向角工況下主館表面數值模擬結果,可以得到如下結論:

(1)主館北立面(迎風面)由屋蓋部分和主體部分組成。屋蓋部分以正壓為主,主要受壓力影響。屋蓋形狀對風壓影響較大,當來流遇到棱角部位,會發生流動分離,形成離散的漩渦,使局部的壓力增大。由于屋蓋形狀不對稱,屋蓋下部東側傾斜率大于西側,流動分離現象更嚴重,導致屋蓋東側平均壓力系數大于西側。屋蓋部分表面最大平均風壓系數為0.3,位置出現在屋蓋東側上部。由于副館的存在,對主館起到遮擋作用,且氣流經過副館會發生流動分離,在主館、副館之間形成漩渦致使北立面主體部分平均風壓系數呈上下對稱分布,中部以負壓為主,平均風壓系數達到-0.1。

(2)主館整體造型大致對稱,東西立面形狀相同,平均風壓系數分布規律相同,均為負值。氣流在東西立面前端發生分離,平均風壓系數沿立面方向遞減,最大負壓系數發生在立面前端,值為-0.5。平均風壓系數等值線基本垂直于氣流流動方向,立面前端等值線密集,平均風壓系數變化梯度較大;沿立面方向,平均風壓等值線逐漸稀疏,變化梯度逐漸減小。

對比東西立面平均風壓系數分布云圖可以發現,由于主館西側存在建筑群,氣流流經時會發生繞流,對主館西面風壓產生影響,致使西面平均風壓系數絕對值略大于主館東面。

(3)主館南立面(背風面)的風壓以負壓為主。雖然主館造型大致對稱,但由于西面建筑群的存在及氣流的繞流作用,南立面風壓系數并不是對稱分布。平均風壓系數絕對值由西至東逐漸減小,由負變正。最大負平均風壓系數出現在凹進部分西側,值為-0.4;最大正平均風壓系數出現在凹進部分東側,值為0.05。

(4)主館頂面的風壓以負壓為主,整體上平均風壓系數絕對值沿來流方向遞減,等值線逐漸變稀疏,變化梯度逐漸減小。最大負平均風壓系數出現在屋蓋頂面前緣,值為-0.55。由于屋面上存在凸起部分,當氣流流經時,會發生明顯的流動分離及回流現象。流動分離會使凸起部分后方形成較大的負壓區,最大負壓系數為-0.5;回流會使屋面凸起部分前方壓力系數由負變正,最大正壓系數為0.05。

(5)由規范類同體型的體型系數反推得到主館表面平均風壓系數,迎風面為0.625,側風面為-0.547,背風面為-0.390,屋面為-0.469;模擬結果整體上略小于規范值,在屋蓋前端及凸起部位氣流分離嚴重,數值模擬結果大于規范值。

3.2 脈動風壓系數

脈動風壓系數反映體育館表面湍流特性,其大小及分布特征受到來流湍流特性和漩渦脫落特性等因素影響。主館表面的脈動風壓系數分布云圖如圖6所示。

從圖6可以看出:

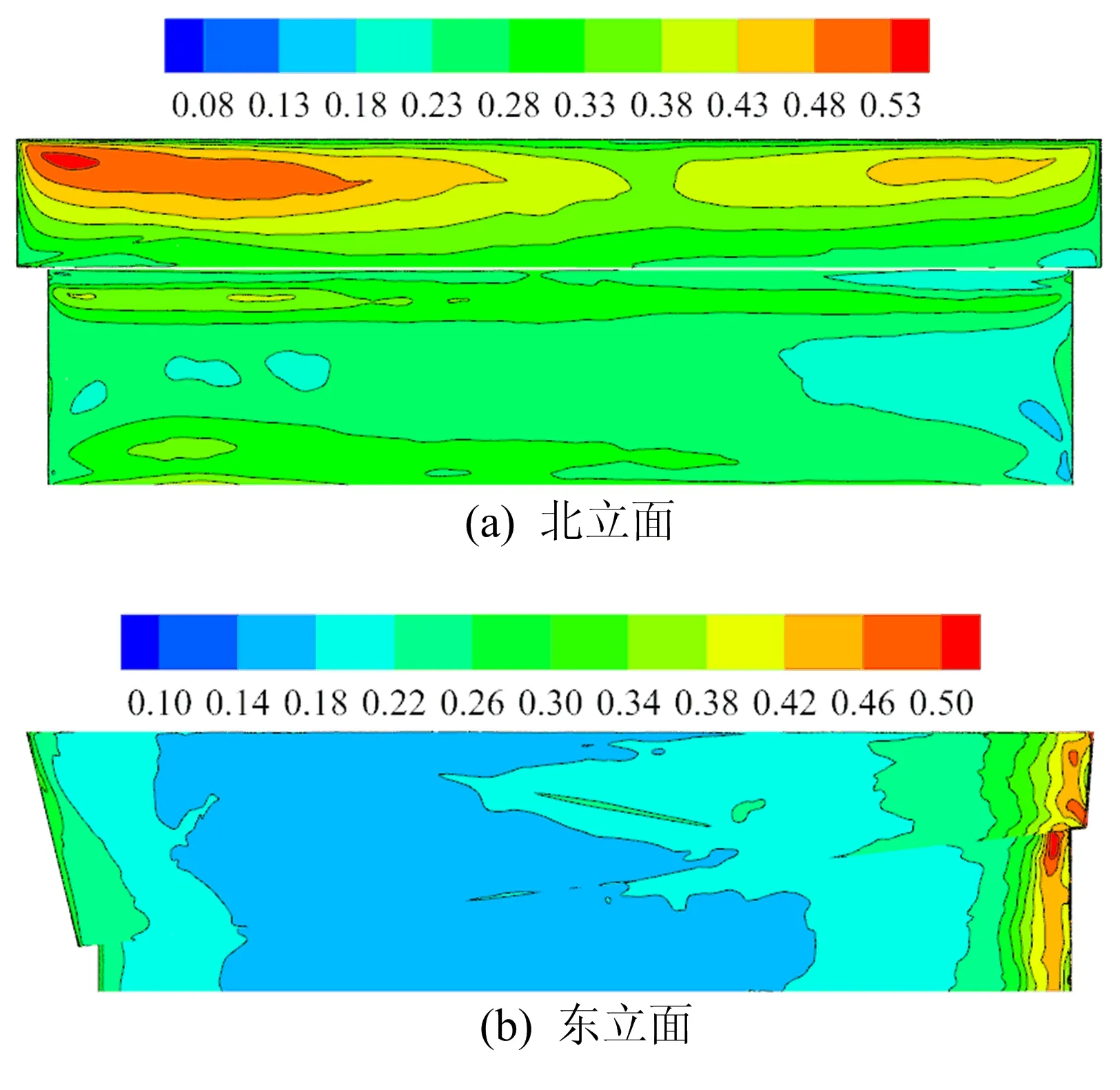
圖6 主館表面的脈動風壓系數分布云圖

(1)主館北、東、西立面的脈動風壓系數分布規律與平均風壓系數分布規律相似,但脈動風壓系數等值線分布更加復雜,這是受到來流中的湍流成分影響造成的。

(2)來流在頂面前端迎風邊緣發生分離、附著現象,因此整體上頂面前端脈動風壓系數大于頂面后端,前端的脈動風壓系數的變化梯度大于后端;在屋面凸起部分,氣流流動分離現象嚴重,因此頂面凸起部位脈動風壓系數急劇增大。

(3)因為主館造型整體上對稱,所以南立面脈動風壓系數分布大致對稱;因為體育館西側、西南側建筑群的干擾作用,所以南立面西側脈動風壓系數略大于東側。

4 數值模擬與風洞試驗對比

4.1 風洞試驗

該大跨度體育館項目的風洞試驗在湖南大學進行,采用HD-3直流式矩形截面邊界層風洞進行高速試驗。體育館模型是由ABS板制成的剛體模型,模型縮尺比為1∶150,高度為23.3 cm,如圖7所示。為了測得體育館主館表面的風壓分布,在模型4個立面及頂面布置了309個測點,如圖8所示。試驗工況與數值模擬一致,以北面來風定義為0°風向,逆時針旋轉,每隔15°為一個工況,共24個工況,風向角示意圖見圖4。

圖7 風洞試驗模型

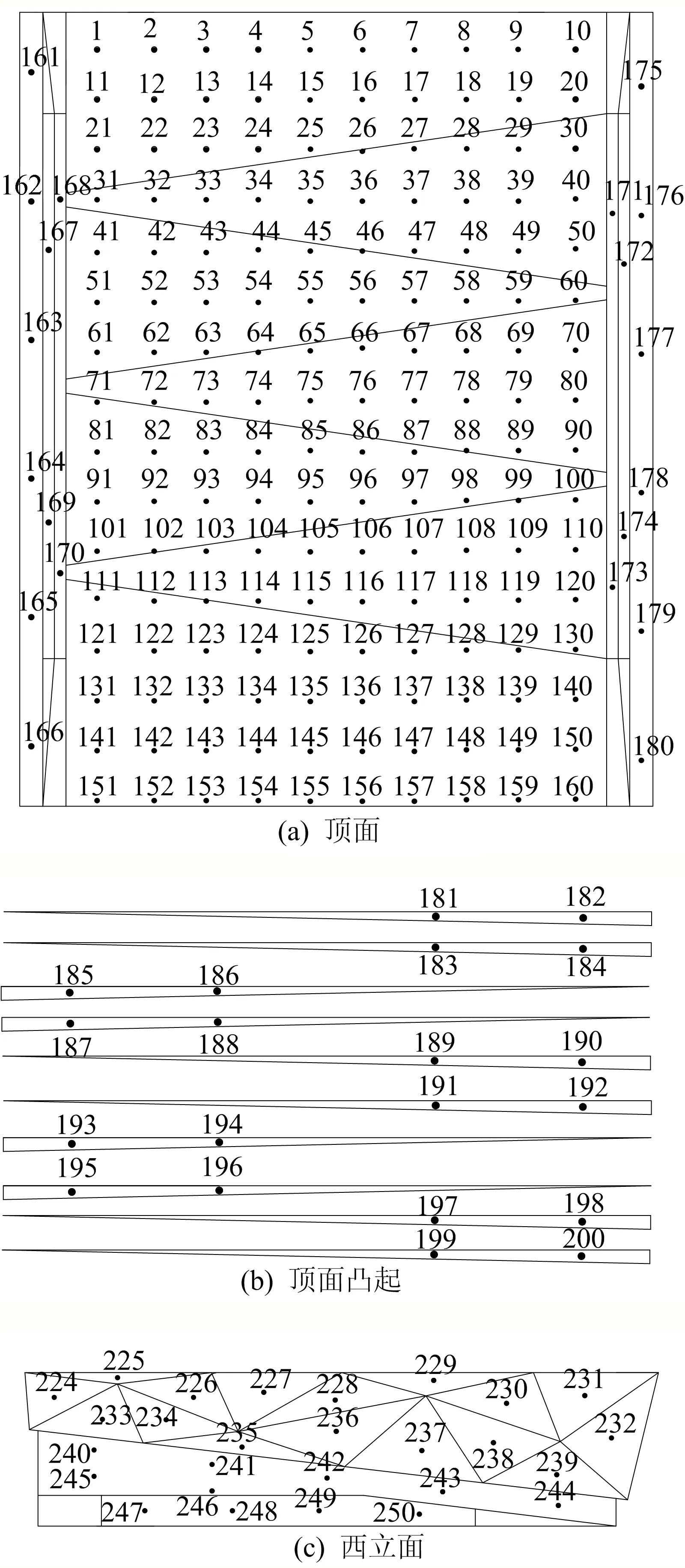
圖8 各測點布置

該體育館周邊建筑密集,為C類地貌[7],即α=0.22。為模擬C 類地貌的大氣邊界層流場,在建筑模型前方設置尖塔陣和粗糙元。在測壓模型風洞試驗中,為保證試驗的準確性,應準確模擬平均風速、風的湍流強度及其積分尺度等,風洞試驗的風速剖面及湍流度剖面如圖9所示。

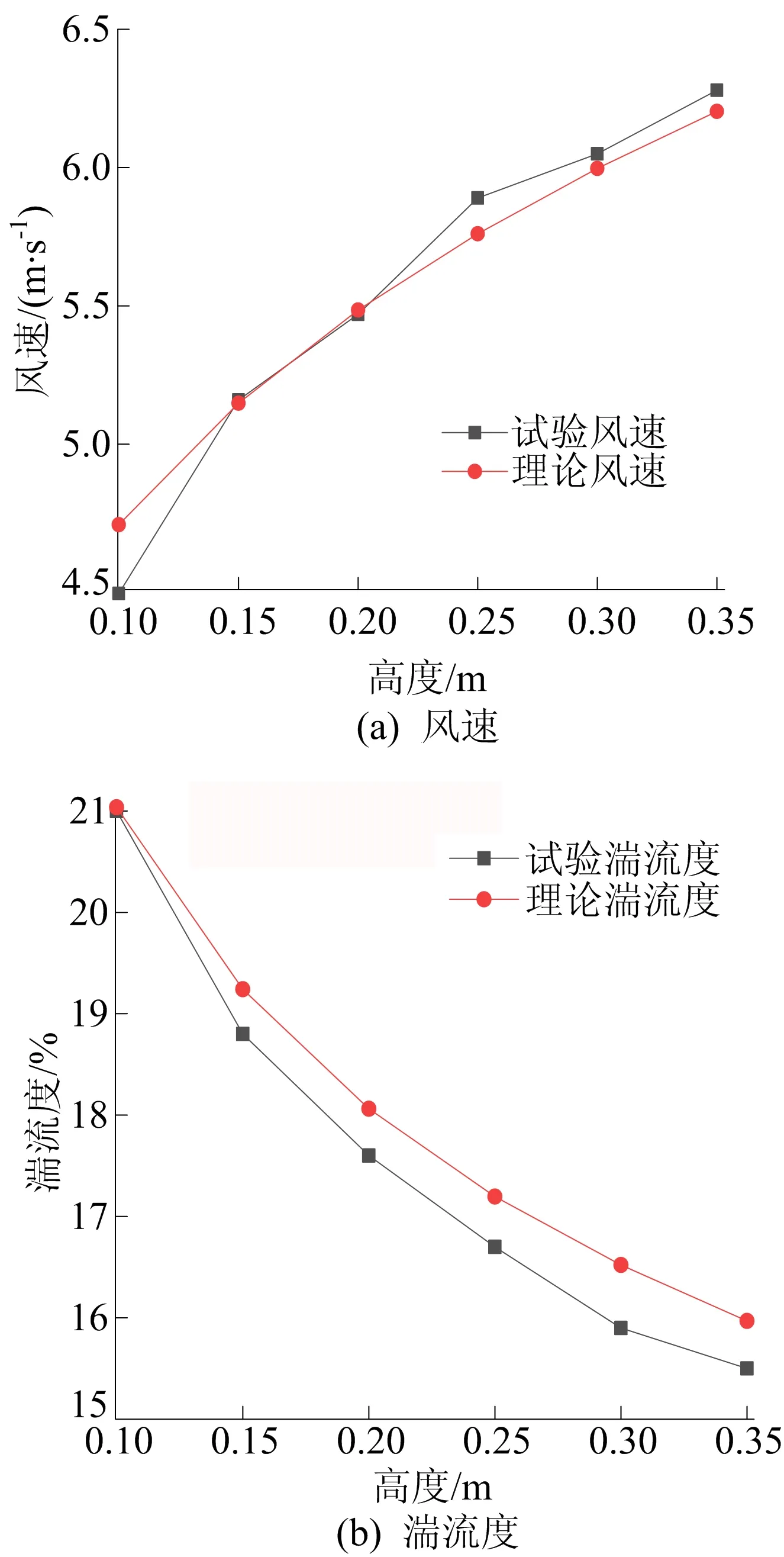
圖9 風洞試驗的風速剖面及湍流度剖面

在大氣邊界層中,平均風速剖面符合指數分布律,其中參考高度zref=0.3 m的風速vref=10 m/s,湍流強度自下而上逐漸衰減,在近地面達到最大值。

4.2 平均風壓系數對比

在體育館主館迎風面、背風面各選取4個典型測點,2個側風面各選取4個典型測點,頂面選取8個典型測點,共計24個測點進行分析,并與風洞試驗結果進行對比,各測點平均風壓系數對比如圖10所示。

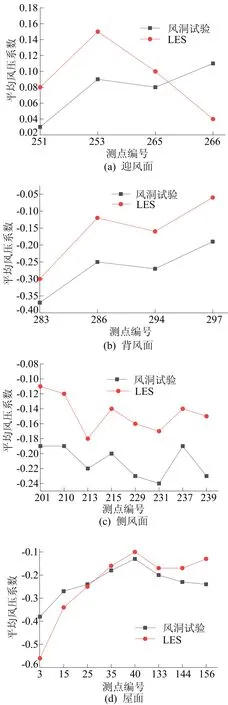
圖10 平均風壓系數對比

從圖10可以看出,LES結果迎風面、背風面、側風面、屋面平均風壓系數分布趨勢與風洞試驗結果一致,迎風面風壓LES結果整體上大于風洞試驗結果,背風面、側風面及屋面風壓LES結果整體上小于風洞試驗結果。考慮到風洞試驗場地大小的限制及試驗縮尺比對試驗精度的影響,風洞試驗僅考慮體育館周邊100 m內建筑,未考慮體育館北側、南側建筑群,LES模擬考慮了體育館周邊900 m內所有建筑,來流風流經體育館北側建筑群發生流動分離,在建筑群后方形成渦旋,使得體育館迎風面風壓增大,背風面、側風面、屋面的風壓減小;因為氣流流經體育館南側建筑群時,受到南側建筑群的阻礙作用會發生回流現象,使體育館背風面的風壓進一步減小,所以背風面LES結果大小與風洞試驗結果差距最大。

4.3 脈動風壓系數對比

體育館主館迎風面、背風面、側風面及屋面典型測點脈動風壓系數LES模擬結果與風洞試驗對比如圖11所示。

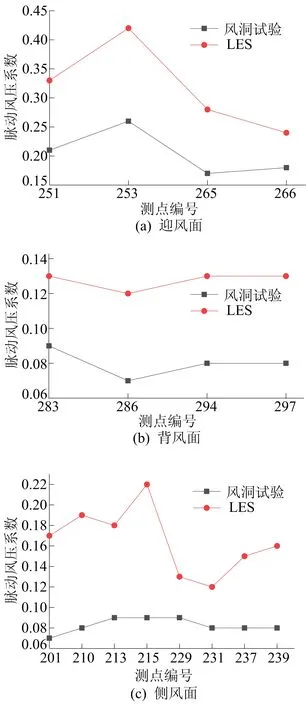
圖11 脈動風壓系數對比

從圖11可以看出,LES結果迎風面、背風面、側風面、屋面典型測點脈動風壓系數分布趨勢與風洞試驗結果吻合,數值上大于風洞試驗結果。流場的脈動風壓受到氣流的湍流強度、渦旋脫落等影響。

因為LES結果考慮了體育館北側建筑群,當氣流流經建筑群時,氣流會發生嚴重的流動分離,在建筑群后方形成許多渦旋,使流場氣流的流動情況更加復雜,所以迎風面、側風面、背風面、屋面的脈動風壓系數均大于風洞試驗結果。因為體育館后方西側建筑的存在,氣流會發生回流現象,所以東側風面的脈動風壓大于西側風面。

5 結 論

本文以合肥某大跨度體育館為研究對象,采用LES方法模擬其表面風荷載,分析了0°風向角下體育館主館表面平均風壓系數及脈動風壓系數分布特征,并與風洞試驗結果進行比較,得出以下結論:

(1)數值模擬得到的表面平均風壓系數整體上小于規范值,但在屋蓋迎風前端及屋面凸起部位,氣流流動分離嚴重,數值模擬結果大于規范值。

(2)主館東、西立面及頂面表面的風荷載以風吸力為主,氣流在前端產生流動分離,風壓梯度變化劇烈。主館頂面凸起部位流動分離現象嚴重,產生極大的負風壓。南立面表面風荷載也以風吸力為主,由于主館西側建筑的干擾,南立面平均風壓系數不是對稱分布,而是西側大于東側。主館北立面為迎風面,以正壓為主,但由于副館的遮擋,在北立面下側出現負壓,且對稱分布。

(3)主館北、東、西立面及頂面的脈動分壓分布趨勢與平均風壓分布相同,分布特性比平均風壓復雜。南立面脈動風壓分布大致對稱,西側略大于東側。

(4)LES模型模擬結果與風洞試驗相近, LES模型為研究建筑物表面的風壓分布規律提供了一種低成本、簡便的方法,其結果可為建筑物的抗風設計提供參考。