基于GeoGebra軟件對“磁聚焦”模型的可視化研究

蔡丁澄，宋善炎

湖南師范大學物理與電子科學學院，長沙 410081

“磁聚焦”模型是高中物理教學中一個重要的二級結論，也是物理高考的熱點問題。在日常教學中發現，很多學生難以建構不同條件下帶電粒子在磁場中運動的模型。為了讓物理模型更加直觀、形象，讓物理教學更加生動、全面，教師可以借助動態數學軟件GeoGebra提供的可視化技術進行輔助教學［1］，幫助學生建構抽象模型。

1 GeoGebra軟件

GeoGebra是一款集幾何、代數和微積分為一體的免費數學教學軟件，它可以從GeoGebra官方網站下載，可以脫機使用。GeoGebra具有幾何畫板的所有功能、Flash的部分功能以及Excel的常用功能。使用者不需要編程也能進行數值模擬，相比于其他教學軟件，GeoGebra更加容易上手使用。抽象化是學生對物理知識的認知常態，利用GeoGebra軟件將抽象的物理知識直觀地展示出來，使物理知識圖像化、具體化，從而有效降低學生的思維難度。因此，GeoGebra軟件是一款非常適合物理可視化教學的輔助工具。

2 “磁聚焦”模型的可視化教學

2.1 “磁聚焦”模型

電荷量相等的帶電粒子以大小相等的速度平行射入勻強圓形磁場，當帶電粒子運動的軌跡圓半徑r與磁場圓半徑R相等時，所有的帶電粒子將匯聚在磁場圓的最低點上，此現象稱為“磁聚焦”，如圖1（a）所示。反之，同種帶電粒子束以相同的速度射入磁場邊界的最低點且R=r時，帶電粒子束經過磁場區域的偏轉后沿相同方向平行射出，這種現象稱為“磁發散”，如圖1（b）所示［2］。

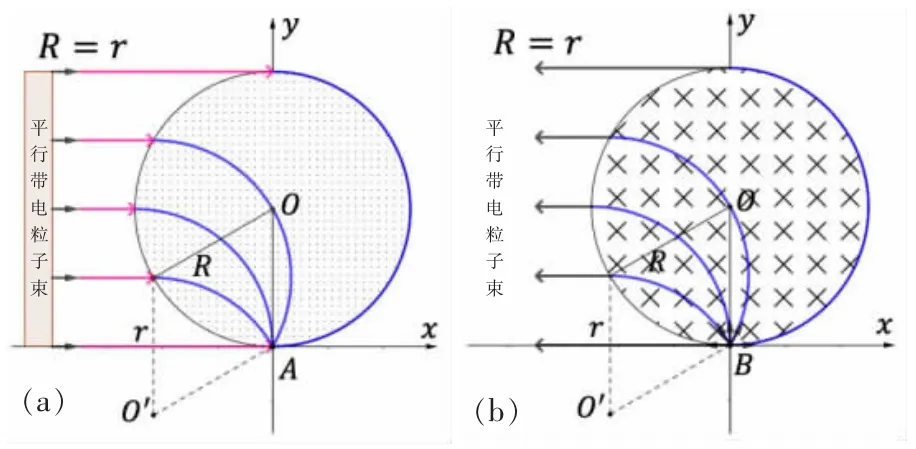
圖1 “磁聚焦”和“磁發散”

2.2 原題呈現

2021年湖南省高考物理第13題是一道典型的“磁聚焦”模型的題目，難度較大。以該題的教學為例，介紹如何利用GeoGebra軟件進行“磁聚焦”模型的可視化教學。

例題（2021年湖南省高考物理第13題）帶電粒子流的磁聚焦和磁控束是薄膜材料制備的關鍵技術之一，帶電粒子流（每個粒子的質量為m、電荷量為+q）以初速度v垂直進入磁場，不計重力及帶電粒子之間的相互作用。對處在xOy平面內的粒子，求解以下問題。

（1）如圖2（a），寬度為2r1的帶電粒子流沿x軸正方向射入圓心為A（0，r1）、半徑為r1的圓形勻強磁場中，若帶電粒子流經過磁場后都匯聚到坐標原點O，求該磁場磁感應強度B1的大小。

（2）如圖2（a），虛線框為邊長等于2r2的正方形，其幾何中心位于C（0，-r2）。在虛線框內設計一個區域面積最小的勻強磁場，使匯聚到O點的帶電粒子流經過該區域后寬度變為2r2，并沿x軸正方向射出。求該磁場磁感應強度B2的大小和方向，以及該磁場區域的面積（無需寫出面積最小的證明過程）。

（3）如圖2（b），虛線框Ⅰ和Ⅱ均為邊長等于r3的正方形，虛線框Ⅲ和Ⅳ均為邊長等于r4的正方形。在Ⅰ、Ⅱ、Ⅲ和Ⅳ中分別設計一個區域面積最小的勻強磁場，使寬度為2r3的帶電粒子流沿x軸正方向射入Ⅰ和Ⅱ后匯聚到坐標原點O，再經過Ⅲ和Ⅳ后寬度變為2r4，并沿x軸正方向射出，從而實現帶電粒子流的同軸控束。求Ⅰ和Ⅲ中磁場磁感應強度的大小，以及Ⅱ和Ⅳ中勻強磁場區域的面積（無需寫出面積最小的證明過程）。

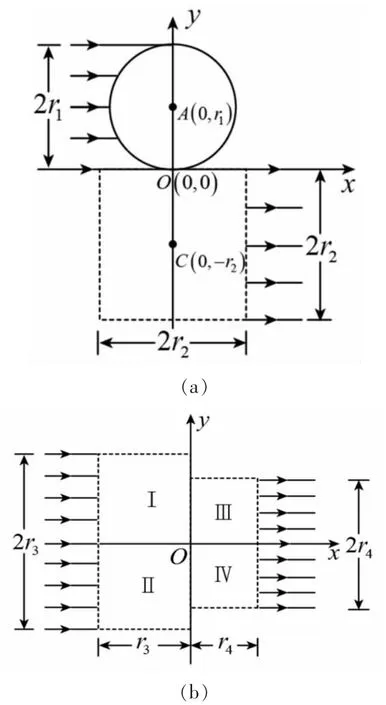
圖2 2021年湖南省高考物理第13題原圖

2.3 具體示例

此考題以磁聚焦和磁控束是薄膜材料制備的關鍵技術為背景，考查的是磁場中的軌道半徑恰好等于磁場圓的半徑時的磁聚焦的問題、最小圓域磁聚焦問題以及平面磁場蝶形磁聚焦問題［3］。問題（1）中，帶電粒子沿x軸正方向射入圓形磁場，要求帶電粒子經過圓形磁場匯聚到O點，滿足磁聚焦的條件。只有帶電粒子的軌跡圓半徑r等于磁場圓半徑r1時，帶電粒子才能在O點匯聚。由粒子在磁場中運動時洛倫茲力提供向心力，可列出關系式：

下面，利用GeoGebra軟件繪制“磁聚焦”模型來求解問題（1）。

第一步，建立題干的背景模型。設置r，r1，α，v的滑動條，α是入射點P和O（0，0）的連線與x軸正方向的夾角。再使用菜單欄的作圖工具在繪圖區繪制出圓心位于A（0，r1）、半徑為r1的圓形磁場區域，磁感線方向垂直紙面向外。描點P（r1sin2α，r1-r1cos2α），Q（r1sin2α-v，r1-r1cos2α），P 為入射點。向量為入射速度，如圖3（a）所示。改變α，模擬帶電粒子從y軸左側的磁場圓邊界平行射入磁場，如圖3（b）所示。

第二步，繪制帶電粒子在磁場區域運動軌跡，如圖3（c）所示。描點O'（r1sin2α，r1-r1cos2α-r），作以O'為圓心、半徑為r的帶電粒子軌跡圓，點C為軌跡圓與磁場圓的交點（由于O'和C點是動點，未在圖中標記）。多次改變r和r1的大小，發現只有當r=r1時，點C與點O重合，帶電粒子才能從O點射出。

第三步，模擬“磁聚焦”模型。改變滑動條α，使帶電粒子流在磁場圓O點匯聚并射出，如圖3（d）所示。

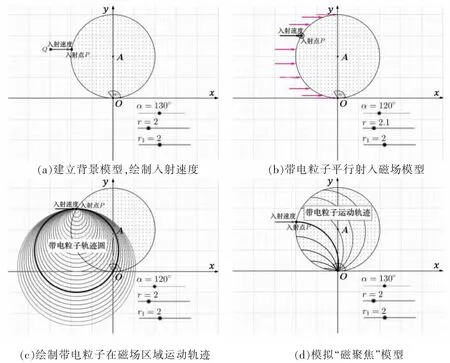
圖3 利用GeoGebra軟件繪制問題（1）中的模型

問題（2）要求粒子從O點進入下方虛線區域后飛出磁場且速度方向與x軸平行，這樣的現象為磁發散過程，即粒子在下方圓形磁場運動的軌跡半徑r等于磁場半徑r2。同問題（1），可得B2=，粒子平行于x軸正方向飛出。根據左手定則，磁場方向為垂直紙面向里。

如果帶電粒子做勻速圓周運動的軌跡半徑r、磁感應強度B2、速度v、質量m、電荷量+q的大小已知，那么能實現“磁聚焦”的勻強磁場最小面積為多大呢？可以通過數學方法，設入射速度與x軸正方向的夾角為θ（0≤θ≤π），帶電粒子軌跡圓圓心為O'（i，j），射出磁場的位置點為Q（x，y）。則可列出關系式：

x=rsinθ；y=rcosθ-r；i=rsinθ；j=rcosθ

解方程，得：

i2+j2=r2；x2+（y+r）2=r2（0≤x≤r，-r≤y≤0）

可知，帶電粒子軌跡圓的圓心位于以（0，0）為圓心、半徑為r的圓周上。射出點位于以（0，-r）為圓心、r為半徑、y軸右側的圓周上。因此，利用微元思想求解，帶電粒子在磁場中運動的速度方向變化角從θ變化到θ+dθ時，對應的運動軌跡包圍的面積為dS，得：

以上是用數學方法解答“磁聚焦”的勻強磁場最小面積的教學過程，但學生理解起來有一定難度。而利用GeoGebra軟件演示粒子的運動過程，可以展示出學生不易想象的物理圖景，引導學生的思考過程，化“難”為“易”，學生的解題思路將會豁然開朗。

第一步，建立題干的背景模型。設置r2的滑動條。再使用菜單欄的作圖工具在繪圖區中繪制出幾何中心位于C（0，-r2）、邊長為2r2的正方形虛線框以及帶電粒子的入射點O（0，0），如圖4（a）所示。

第二步，繪制入射速度。設置v，θ的滑動條，v是速度的大小，θ是速度方向與x軸正方向的夾角。描點P（vcosθ，-vsinθ），使用向量工具，繪制向量為入射速度，如圖4（b）所示。

第三步，繪制射出速度。設置x，y的滑動條。描點Q'（r2sinθ，r2cosθ-r2），R（r2sinθ+v，r2cosθ-r2），使用向量工具，繪制向量為射出速度，如圖4（c）所示。

第四步，模擬射出點變化軌跡。通過改變θ滑動條，可以清楚地演示帶電粒子射出點的軌跡變化，如圖4（d）所示。

第五步，繪制帶電粒子在磁場區域的運動軌跡。描點O'（r2sinθ，r2cosθ），O'為帶電粒子軌跡圓圓心。以O'為圓心、半徑為r2作圓。利用圓弧工具，繪制帶電粒子在磁場區域運動軌跡，如圖4（e）所示。

第六步，模擬帶電粒子在磁場區域的變化軌跡。通過改變θ滑動條，可以清楚地演示帶電粒子在磁場區域的運動軌跡是以C（0，-r2）為圓心、半徑為r2的圓，如圖4（f）所示。這也是實現“磁聚焦”的最小勻強磁場區域，其面積大小為

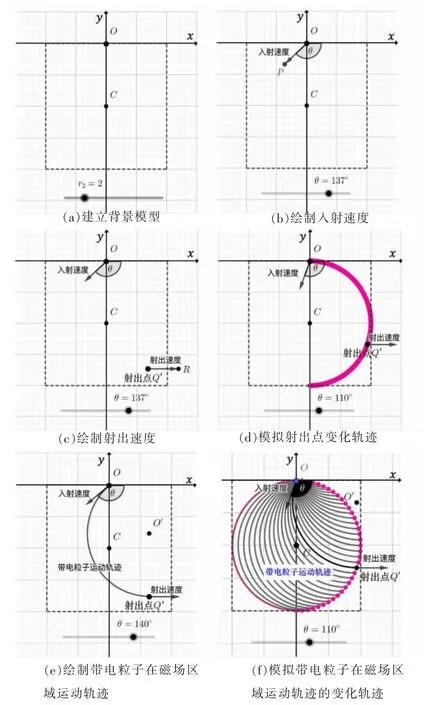
圖4 利用GeoGebra軟件繪制問題(2)中的模型

通過代數及指令輸入，可以精確繪制模型，使用滑動條實現圖形的動態變化，從而演示可實現“磁聚焦”的最小勻強磁場區域。

問題（3）與問題（2）的求解方法類似。根據左手定則，可以判斷出Ⅰ和Ⅲ區域的磁場方向。由洛倫茲力提供向心力可以列出等式，從而求得Ⅰ區域和Ⅲ區域的磁感應強度大小。分析可知，一部分帶電粒子從Ⅰ區域入射，經過磁場區域的偏轉后在O點匯聚，再從O點射入到Ⅳ區域進行偏轉運動，最后平行于x軸正半軸射出。另一部分帶電粒子是從Ⅱ區域入射經過磁場區域的偏轉后在O點匯聚，再射入到Ⅲ區域進行偏轉運動后平行于x軸正半軸射出。

下面以Ⅰ和Ⅳ區域為例，利用GeoGebra軟件演示帶電粒子的運動軌跡，并模擬出Ⅰ和Ⅳ區域的最小磁場區域。與問題（2）的繪制步驟相似。首先，選擇合適的工具繪制出四個區域，再設置β滑動條，β為粒子射出Ⅰ區域時速度與x軸正半軸的夾角。然后，根據入射點與射出點（匯聚點）的幾何關系，繪制出入射點位置和入射速度。再根據入射點與軌跡圓圓心的幾何關系，找出軌跡圓的圓心O'，作出軌跡圓。最后，利用圓弧工具，作出帶電粒子在磁場區域的運動軌跡。改變β滑動條，帶電粒子束在磁場區域運動軌跡所覆蓋的區域就是最小的磁場面積（圖5），其值為同理，Ⅱ和Ⅳ區域的最小磁場區域像兩片“綠葉”［4］，其面積分別為

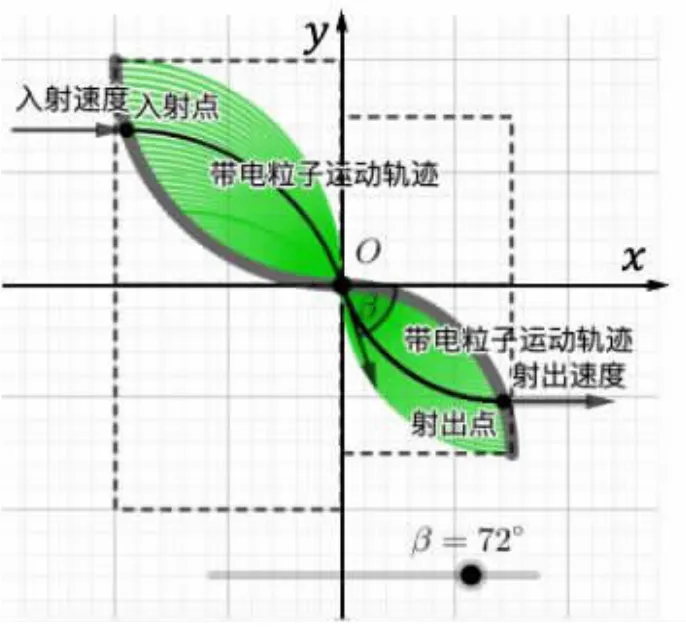
圖5 兩片“綠葉”：最小磁場區域

3 結語

借助GeoGebra軟件的多功能幾何繪圖工具進行可視化教學，可以將較難的抽象思維模型直觀地呈現在學生面前，讓學生在學習過程中充分理解“磁聚焦”這個二級結論。這種融合信息技術的物理教學過程，不僅能有效提高學生的學習效率，而且能有效培養學生的模型建構能力，提升學生的學科核心素養，值得應用和推廣。