基于改進LSTM-Prophet算法的客運量預測

陸 奕，郭唐儀

(南京理工大學自動化學院，江蘇 南京 210094)

針對我國的鐵路路網日益完善，各省各區之間的聯系更加緊密，鐵路的客運量也隨之提升的現狀，各專家學者對公路、鐵路、航運和水運的客流量內在規律有很多研究，提出多種方法模型以達到預測各客流量的目的。牛坤等通過自回歸移動平均模型(ARIMA)進行短時客流預測并優化票額制度[1]；李萬等通過粒子群算法與長短時記憶神經網絡的組合預測模型，對鐵路客運量數據預測[2]；王素麗等應用灰色Markov鏈模型預測鐵路客運量，并證明其預測精度高于經典灰色模型[3]；袁勝強通過對比分析灰色模型和BP神經網絡模型的優劣，最終采用馬爾科夫鏈模型對灰色BP神經網絡的組合模型進行優化，并使用優化后的組合模型對甘肅省鐵路客運量進行預測[4]；湯銀英等經過深入研討鐵路月度客運量的季節性波動，發現鐵路月度客運量符合季節波動性，故通過SARIMA模型預測鐵路月度客運量數據[5]；錢名軍等根據鐵路月度時間序列數據的趨勢性、季節性和波動性，建立SARIMA-GARCH模型，經證明該模型可有效消除模型殘差的異方差性，提高預測精度[6]。Glisovic等通過比較參數法和非參數法，將遺傳算法和人工神經網絡兩種模型組成混合模型，并用該混合模型預測塞爾維亞的鐵路月度客運量數據，則預測效果較優[7]。JIA等結合GM模型與ARIMA模型，構造混合模型從而研究預測客流變化[8]。

現有方法雖然能一定程度預測客運量，但鐵路客運量并不是受單一因素的影響，而是會受較多要素影響，如各休息日、法定節假日、寒暑假等。2020與2021年春節期間，在新冠疫情的影響下，政府實施了一系列科學的防疫措施，包括鐵路、公路、城市公共交通等停運措施，封閉式管理措施與推遲開學與復工等措施，各地人民也積極響應政府號召，實施居家防疫，減少了不必要的出行，鐵路客運量因此有明顯的縮減[9]。這些舉措都會給鐵路客運量帶來波動變化，所以在這關鍵時刻，本文提出LSTM-Prophet模型，運用該模型預測2019年的客運量月度數據，試驗表明該模型能夠對節假日客運量的波動有更精準預測，則通過LSTM-Prophet模型能夠預測精度較高的客運量，從而了解疫情帶來的影響，能為鐵路部門未來規劃提供參考和建議。

1 優化的LSTM模型

1.1 傳統的LSTM模型

LSTM神經網絡解決了RNN梯度消失、對前層網絡參數無法學習等問題，從而改進RNN，提高預測精度。LSTM是采取增加門控系統來解決RNN存在的問題[10]，故LSTM存在三個門：Input Gate、Output Gate、Forget Gate，單元結構圖如圖1。

圖1 LSTM單元結構圖

Input Gate計算公式

it=σ(Wi·[ht-1,xt]+bi)

(1)

(2)

(3)

Output Gate計算公式

ot=σ(W0·[ht-1,xt]+b0)

(4)

ht=0t·tanh(ct)

(5)

Forget Gate計算公式

f(t)=σ(Wf·[ht-1,xt]+bf)

(6)

1.2 算法改進和參數優化

(7)

圖2 改進LSTM算法

同時利用高斯過程作為先驗函數，采用Expected-improvement(EI)作為采集函數，對1-LSTM和2-LSTM進行超參數優化。

2 LSTM-Prophet模型

2.1 Prophet算法

Prophet算法是Facebook發布的一個開源庫，它是一個可分解的模型，即趨勢、季節、節假日模型，它可以用非復雜且直觀的參數對時間序列進行較高精度預測。但與其他較為經典的時間序列預測模型不同的地方在于，Prophet模型會先對序列采取周期性的分解，然后再預測。這樣的預測方式，會突出數據中的節日效應和變化趨勢，尤其當存在數據缺失、趨勢突變和異常值的等問題的情況下，其魯棒性效果優異。

Prophet把時間當做回歸元，通過嘗試擬合線性和非線性的時間函數項，通過采取與Holt-Winters指數平滑的類似辦法，將考慮額外干擾因子季節因素進行建模[12]。整個過程可以分為四個部分：Modeling、forecast Evaluation、Surface Problems以及Visually Inspect Forecasts。

Prophet模型是自加性模型的一種，可以通過對趨勢項建模、周期項建模和節假日項建模，從而分解時間序列，最終形成模型，故可表示為[13]

y(t)=g(t)+s(t)+h(t)+εt

(8)

其中：g(t)為趨勢項，用于擬合序列中的非周期變化，包括分段線性增長，邏輯增長等。通常，Prophet采用線性模型進行預測。在對核心項趨勢項進行建模時，當預測值是增長的情況時，也不是無限制性增長，將會存在一個可無限接近到達的最大極限值，此時該值這被稱做承載容量(carrying capacity)，預測值在接近該值時將趨于飽和。

h(t)為節假日項，用于存在無規律性的節假日所帶來的影響。法定節假日、重大事件或者突發事件會對序列產生很大的影響，數據波動會比較劇烈，而各較為穩定的節假日帶來的波動在Prophet模型中是可以預測的。將各節假日設為一個模擬變量Di，共有L個虛擬變量，并且假設該模擬變量對客運量造成的影響為Ki，那么聯立二者可得如下矩陣，從而將模型中納入影響因子，達到提高模型預測精度的目標

Z(t)=[1(t∈D1),…1(t∈DL)]

(9)

h(t)=Z(t)K

(10)

s(t)用于周期變化，可稱為周期項，該項較常使用傅里葉技術，表達式如下

(11)

式中:P是周期；an,bn是被估參數；t是時間；n是使用周期數的一半，N是使用周期的個數。Prophet模型在大多數情況下都是用來擬合連續時間段的時間序列，例如對年的周期性，P的值取365.25，N值取10，對周的周期性，P的值取7，N值取3。

εt用于反應未在模型中體現的異常變動，即誤差項。

2.2 LSTM-Prophet算法模型

Prophet是單特征模型，其輸入變量是僅輸入兩列，分別是設日期“ds”，數值輸入“y”。有因為存在承載容量，故Prophet模型將有三種預測值。預測值設置為：預測值yhat，預測下界yhat_lower與預測上界yhat_upper。

在構建LSTM-Prophet算法模型時，首先根據優化后的LSTM模型，進行預測分析，再將預測結果作為輸入進行Prophet算法預測，最后可得最終預測數值。

3 鐵路月度客流量分析與預測

本文采用2005年1月～2018年12月的鐵路月度客運量數據作為數據樣本進行擬合建模分析，本文數據來源于國家統計局。通過LSTM-Prophet模型對2019年1～12月的月度數據進行預測，并對比分析該模型與傳統灰色模型GM(1，1)，季節差分移動自回歸模型(SARIMA)，LSTM神經網絡的優劣，從而比較分析LSTM-Prophet模型。

3.1 改進的LSTM模型

采用PyTorch深度神經網絡框架搭建本模型，實驗在Intel(R)Xeon(R)CPU E5-2660 v2處理器和NVIDIA GeForce GTX Titan X顯卡上進行。在對數據集做10 000次訓練后，得到如圖3的擬合情況，由圖可知，擬合情況沒有非常理想，預測精度不夠高。

圖3 LSTM預測擬合圖

2019年各月度數據具體如表1，由表1可知，精度的波動略大，最高達15.25%，最低為0.01%。

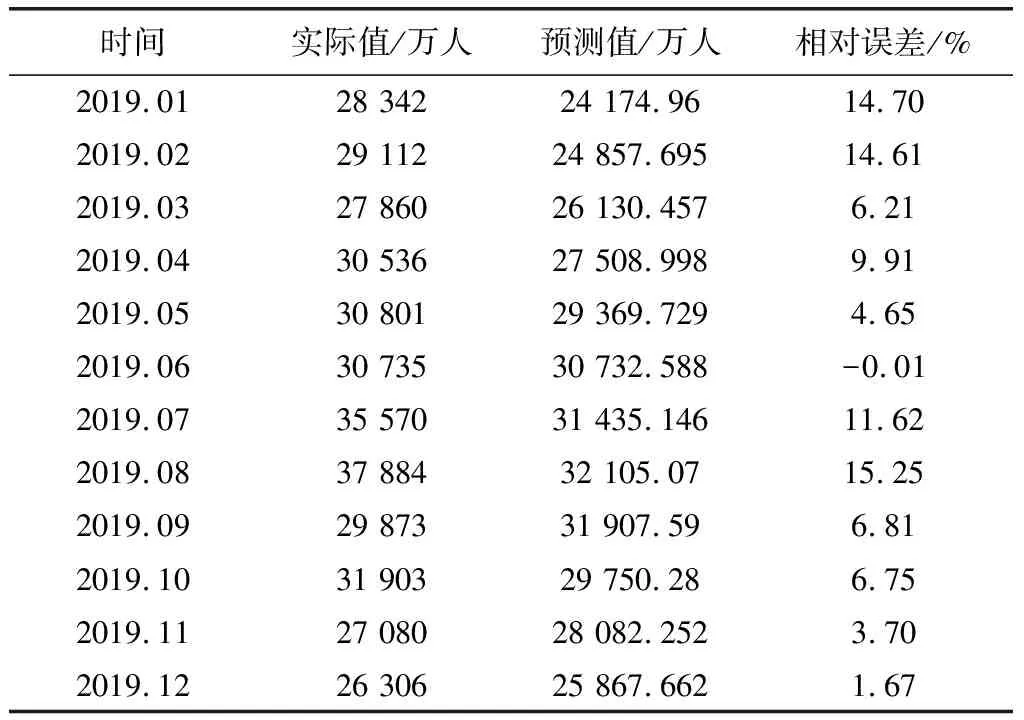
表1 LSTM預測值

圖4 LSTM-Prophet預測擬合結果

3.2 LSTM-Prophet模型

為建模的準確性與減小數據的振動幅度，故先將月度數據進行數據預處理，即將數據做log處理取其對數。又由于Prophet基本模型可知，Prophet模型是對天等連續時間的處理，所以如果直接用鐵路客運量的月度數據進行擬合，那么結果將會誤差很大，預測精度將會較低。為了解決這一問題，故將通過make_future_dataframe中傳入頻率參數的方式，讓模型只做月度預測，從而達到預測要求。將改進后的LSTM模型預測值作為輸入，得到擬合曲線如圖4，結果如表2。

表2 LSTM-Prophet預測結果

3.3 模型對比

本文采用平均絕對百分比誤差MAPE、平均絕對誤差MAE與均方根誤差RMSE為評價指標，指標計算公式如下

(12)

(13)

(14)

式中：Yt為預測值，yt為實際值，n為預測次數。

對比分析各模型的預測結果，用四種模型進行預測，比較四種模型的MAPE值、MAE值與RMSE值，其中LSTM-Prophet的MAPE值、MAE值和RMSE值均為最低值，分別為1.91%，559.07和691.82，全面優于GM(1，1)模型的8.75%，2 892.73和4 036.76、LSTM神經網絡的7.99%，2 512.77和3 029.43與SARIMA(3，1，1)(1，1，1)12的2.76%，816.66和957.19。故得出GM(1，1)模型的預測精度是四種模型中最低的，其次為LSTM神經網絡，再次為SARIMA(3，1，1)(1，1，1)12模型，Prophet模型精度為最高。所以LSTM-Prophet模型更適合用于預測鐵路月度客運量，為規劃提供參考，結果如表3。

表3 四種模型對比表

4 結 論

LSTM-Prophet模型對于歷史數據中包含的節假日效應有很強的敏感性，使其預測結果更加接近于預測值，從而提高預測精度。本文通過提取2005年1月～2019年12月的月度的季節性規律，改進優化了LSTM模型，并建立了LSTM-Prophet模型，且對2019年1～2月的客運量擬合預測，并與傳統的GM(1，1)模型、SARIMA(3，1，3)(1，1，1)12模型和LSTM神經網絡的預測結果對比分析，得出LSTM-Prophet模型更能準確預測鐵路月度客運數據，對于研究鐵路客運數據預測有一定參考意義，可對鐵路部門開展工作提供參考價值。但該模型雖在遇到不可抗力因素時依舊無法及時準確做出調整，但可以根據預測數據了解因素對客運量的影響。