基于熵掩蔽的DCT域恰可察覺失真模型

駱瓊華，王鴻奎，殷海兵，邢亞芬

基于熵掩蔽的DCT域恰可察覺失真模型

駱瓊華，王鴻奎，殷海兵，邢亞芬

（杭州電子科技大學通信工程學院，浙江 杭州 310018）

為提高離散余弦變換（discrete cosine transform，DCT）域恰可察覺失真（just noticeable distortion，JND）模型閾值精度并避免跨域操作，將熵掩蔽效應引入DCT域JND模型。首先，從自由能理論和貝葉斯推理出發，設計基于DCT域紋理能量相似性的自回歸模型模擬視覺感知過程中的自發預測行為；其次，探索視覺感知與預測殘差的映射關系得到塊級無序度，并將熵掩蔽效應建模為關于無序度的JND閾值調節因子；最后，結合空間對比敏感度函數、亮度自適應掩蔽以及對比度掩蔽，提出基于熵掩蔽的DCT域JND模型。與現有DCT域JND模型相比，所提模型所有運算均在DCT域執行，更高效簡潔。主觀、客觀實驗結果表明，所提模型在感知質量相同或更好的情況下，噪聲污染圖的平均峰值信噪比（peak signal-to-noise ratio，PSNR）值比其他4個JND對比模型低2.04 dB，更符合人眼視覺系統的感知特性。

恰可察覺失真；人眼視覺系統；熵掩蔽效應；自由能理論；貝葉斯推理

0 引言

人類視覺系統（human visual system，HVS）由于其潛在的生理和心理機制無法感知一定閾值以下的圖像失真，這一閾值被稱為恰可察覺失真（just noticeable distortion，JND）閾值[1]。JND模型揭示了人類視覺系統對圖像失真的感知特性，被廣泛應用于圖像和視頻處理中，如圖像和視頻壓縮/編碼[2]、質量評價[3]、數字水印[4]和圖像增強[5]等。

過去二十年里，JND閾值估計取得了巨大進展。現有JND估計模型根據計算域可分為兩類：像素域JND模型和子帶域JND模型。其中，像素域JND模型直接計算圖像和視頻中每個像素的JND閾值[6]；子帶域JND模型主要在壓縮域中估計JND閾值，如小波域和DCT域[7]。本文重點關注基于DCT域的JND閾值估計，因為DCT域JND模型可直接應用于基于DCT變換的圖像/視頻壓縮領域[2]。

DCT域JND模型主要由對比敏感度函數（contrast sensitivity function，CSF）、亮度自適應（luminance adaptive，LA）掩蔽效應和對比度掩蔽（contrast masking，CM）效應構成[7]。縱觀現有JND模型，其核心問題是如何準確高效地估計CM模型。DCT域CM模型通常將圖像塊分為3種類型（即平面、邊緣和紋理），并為這3種類型設置3個不同的權重以突出紋理區域[7]。然而內部生成機制（internal generation mechanism，IGM）對有序紋理內容是自適應的，因此這些有序紋理區域會被高估。

實際上，HVS并非逐字翻譯輸入場景，而是通過IGM主動推斷輸入場景[8]。自由能理論為人類的行為、感知和學習提供了統一的解釋，其基本思想是所有的適應性生物制劑都能抵抗紊亂的自然趨勢[9]。HVS在自由能理論的指導下試圖處理盡可能多的結構信息而避免不確定信息。這一特性揭示了HVS的感知局限性，包含大量不確定信息的無序紋理區域的JND閾值往往相對較高。近年來，自由能理論已被引入像素域JND模型中進行有意義的探索[10]。Wu等[10]通過貝葉斯預測模擬視覺系統自發的預測行為，將圖像分為有序成分和無序成分進行獨立處理，以熵掩蔽（entropy masking，EM）的形式引入像素域JND閾值估計。在此基礎上，Wu等[11]引入模式掩蔽取代熵掩蔽和對比度掩蔽，并提出一個增強型的像素域JND模型。Zeng等[12]利用相對全變分模型和方向復雜度，將圖像分成結構圖像、有序紋理圖像和無序紋理圖像，并結合視覺顯著性構建像素域JND模型。Liu等[13]將屏幕內容圖像分解為屏幕內容集和非屏幕內容集進行處理，并研究了邊緣掩蔽和模式掩蔽的組合掩蔽效應。Wang等[14]根據分層預測編碼理論將視覺感知分為3個階段，并結合正負感知效應提出一個新的像素域JND模型。

基于上述自由能理論在像素域JND閾值估計中的探索，本文認為在DCT域JND閾值估計中合理引入自由能理論與熵掩蔽效應將有助于提高DCT域JND模型的準確性。由于大多數圖像/視頻資源以壓縮形式進行有效存儲和傳輸，直接對壓縮數據而非其解壓縮版本進行操作變得非常重要。本文擬在避免跨域運算的前提下，引入熵掩蔽效應并提出DCT域JND建模方法。

1 DCT域JND模型概述

1.1 DCT域JND模型框架

本文主要研究基于DCT域的JND閾值估計。對于×大小的DCT塊，第(,)個DCT系數計算式如下。

通常，DCT域JND模型被表示為多個調節因子的乘積，這源于Watson[15]的DCTune模型。本文提出的JND模型主要考慮4種掩蔽效應，計算如下。

1.2 CM模型改進

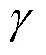
其中，是頻率線性函數梯度，計算同Bae[7]的模型。引入抑制因子前后對比如圖2所示，截取邊緣區域（即黑色方框區域）進行更清晰的對比，通過引入抑制因子，邊緣塊的對比度強度被有效抑制，邊緣區域的圖像質量也得到明顯改善。

圖2 引入抑制因子前后對比

2 基于熵掩蔽的JND閾值調節因子

2.1 貝葉斯預測模型

HVS在自由能理論的指導下可以準確預測并充分理解有序內容，同時粗略感知無序內容[9]。顯然，與無序區域相比，HVS對有序區域更敏感，其JND閾值更小。由于貝葉斯推理是信息預測的有力工具，本文采用貝葉斯大腦理論[19]模擬人腦中的IGM進行有序信息預測，并建立DCT域自回歸預測模型。貝葉斯大腦理論的基本原理是，大腦有一個試圖以最小誤差概率表示傳感器信息的模型[19]。對于圖像而言，貝葉斯大腦系統以最大化條件概率表示像素值。

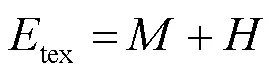
圖3 DCT域貝葉斯預測示例

圖4 8×8 DCT塊能量分布

對于邊緣區域，HVS應能自適應地進行預測。如圖3（b）所示，中心塊位于平坦區域的一條直線（即邊緣區域）上時，應當只由同處邊緣區域的周圍塊進行預測。因此，本文采用DCT域的TE塊分類法[18]將圖像分為邊緣塊和非邊緣塊進行預測。當中心塊為邊緣塊時，僅由同為邊緣塊的周圍塊進行相似度加權預測；當中心塊為非邊緣塊時，僅由非邊緣塊進行相似度加權預測；而當中心塊為邊緣塊（非邊緣塊）且其周圍塊均為非邊緣塊（邊緣塊）時，中心塊由周圍8個塊共同預測得到。

DCT域貝葉斯預測結果如圖5所示，本文獲得的預測圖像和殘差圖像存在明顯的塊效應，這是由8×8的DCT所引起的。為證明本文預測模型的準確性，采用多尺度結構相似性（multi-scale structural similarity，MS-SSIM）指數度量預測圖像與原始圖像之間的相關性，高于0.5的MS-SSIM指數值表明圖像間具有很強的相似性[20]。從圖5（b）及其對應的MS-SSIM指數值可以看到，本文提出的DCT域貝葉斯預測模型能較為準確地預測圖像內容。

圖5 DCT域貝葉斯預測結果

2.2 熵掩蔽模型

由于DCT后絕大部分能量都集中在左上角的低頻系數中，DCT系數之間幅度相差很大。而DCT系數幅度越大，其預測殘差往往越大。因此這里將DCT系數殘差與原始系數值相除，并對其相除結果進行歸一化處理得到無序度塊。第個DCT塊的無序度由其無序度塊求平均得到，計算如下。

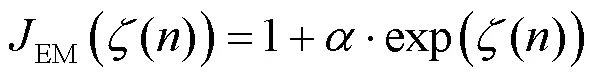
其中，是比例因子，根據主觀觀看結果，按照經驗將其設為0.15。這里選取“IVC”數據集[22]中的一幅圖像，給出主觀質量對比的例子，不同值得到的主觀質量對比如圖6所示。從主觀質量的角度可以看到，當在取0.1和0.15時圖像主觀質量相近，而時主觀質量明顯受損；從噪聲隱藏能力的角度，可以看到依次取0.15和0.2時，PSNR值分別降低0.71 dB和0.27 dB。綜上所述，取0.15時可以在不影響圖像質量的情況下降低較多的PSNR值。

3 實驗結果與分析

3.1 對比實驗

本文提出的JND估計模型是在DCT域中結合EM效應而構建的。因此為驗證本文DCT域JND模型的有效性，這里選擇研究工作相近的3個JND模型進行對比實驗，分別命名為Zeng2019[12]、Liu2020[13]以及Li2022[25]。其中，Zeng2019和Liu2020是考慮自由能理論的兩種像素域JND模型，而Li2022是融合邊緣掩蔽與中心凹掩蔽的像素域JND模型。

通常在更精確JND模型的指導下，圖像能保持感知質量不變并隱藏更多噪聲。在基于DCT域的JND估計中，噪聲被添加到圖像中的每個DCT系數[24]，如式（13）所示。

JND模型的噪聲容忍能力是用峰值信噪比（peak signal-to-noise ratio，PSNR）衡量的，即相同感知質量下PSNR越低，JND模型估計越準確。8位灰度圖像的PSNR由原始圖像和噪聲注入圖像之間的均方誤差（mean squared error，MSE）計算得到，如式（14）所示。

由于圖像的最終接收者為人眼，僅以PSNR評估JND模型性能不夠準確，因此采用MS-SSIM指數和平均意見分數（mean opinion score，MOS）評價圖像的主觀質量。其中，MS-SSIM指數通過圖像間結構相似性評估圖像質量，是一種更適合HVS的感知質量評價指標[26]。本文根據ITU-R BT.500-11標準展開主觀質量評估（subjective quality assessment，SQA）實驗[24]，該實驗用于測量原始圖像和噪聲注入圖像間的主觀質量差異。每次測試中，為了更好地比較主觀質量，將原始圖像作為標準放在左邊，4個注入噪聲的圖像（本文模型和用于對比的3個模型）以隨機順序在右邊并列顯示。主觀評價標準和分數被分為4個等級，以指示噪聲注入圖像相對于原始圖像的失真程度。評價標準具體為：“0”表示右邊圖像質量沒有下降，“-1”表示輕微下降，“-2”表示下降較多，“-3”表示下降嚴重。25位視力正常或矯正視力正常的受試者被邀請評估噪聲注入圖像的感知質量，個人評價分數以MOS的形式提供。在SQA實驗中，顯示器的分辨率為1 920 dpi×1 080 dpi，并將觀看距離設置為顯示屏高度的4倍[24]。

3.2 性能評估

JND模型的性能是以PSNR、MS-SSIM指數和MOS衡量的。被測JND模型的良好性能意味著由JND模型注入噪聲的圖像與其他模型相比具有更低的PSNR值以及更高的MS-SSIM指數值和MOS值。表1～表3展示了注入相同噪聲后本文模型與其他3個模型在不同圖像數據集上的PSNR、MS-SSIM指數和MOS值，其中由于MS-SSIM指數值相差較小，在這里保留3位小數。為了更直觀地對比JND模型性能，采用柱狀圖的形式描述不同JND模型在3個數據集上主客觀評價指標的平均值，如圖7所示。本文以PSNR測量JND模型隱藏噪聲的能力。由表1～表3可知，本文模型在3個分辨率不同的數據集上均具有最低的PSNR值。具體而言，本文模型在3個數據集上獲得的平均PSNR值為26.75 dB，分別比其他模型低2.52 dB、2.12 dB和1.47 dB，如圖7（a）所示。此外，本文以MS-SSIM指數和MOS測量噪聲注入圖像的感知質量。由表1～表3可知，本文模型在3個數據集上均獲得最高的MS-SSIM指數值和MOS值。具體來說，本文在3個數據集上獲得的平均MS-SSIM指數值為0.963，分別比其他3個模型高0.020、0.018和0.023，如圖7（b）所示；而平均MOS值為-0.29，比其他模型高出0.17、0.13和0.16，如圖7（c）所示。由此可見，與其他3個模型相比，本文提出的DCT域JND模型更精確，能隱藏更多噪聲，獲得更好的圖像感知質量。

表1 不同JND模型在“IVC”數據集上的性能對比

表2 不同JND模型在“TID2013”數據集上的性能對比

表3 不同JND模型在“LabelMe”數據集上的性能對比

注：加粗字體為最優結果。

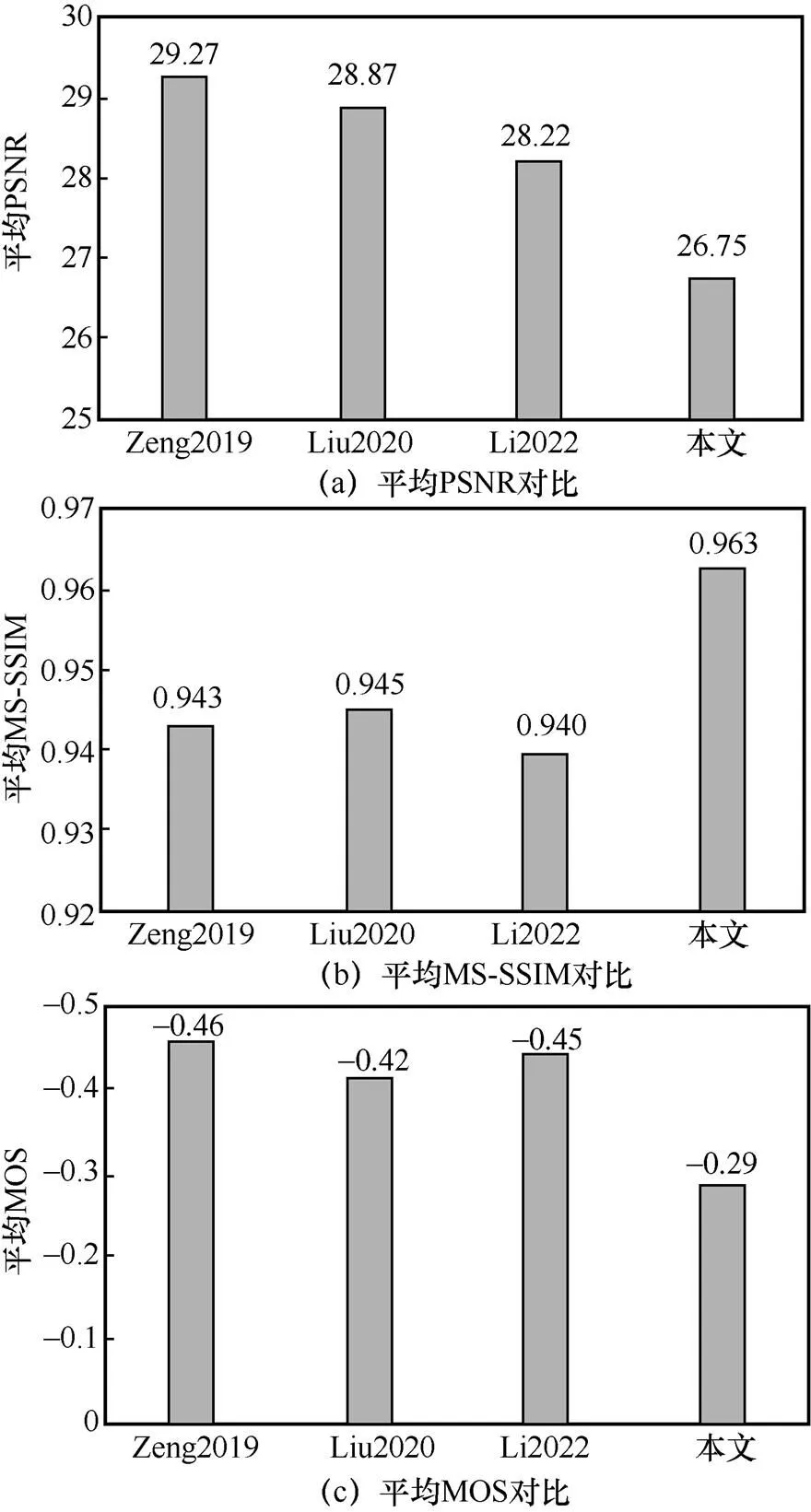
圖7 不同JND模型在3個數據集上的主客觀指標平均值對比

圖8 不同JND模型在“”圖像上的對比

圖9 不同JND模型在“”圖像上的對比

圖10 不同JND模型在“”圖像上的對比

以上主觀、客觀實驗證明，本文提出的JND模型能充分考慮人眼視覺特性，在平坦、有序紋理、無序紋理區域分別注入少量、適量、大量噪聲，實現噪聲的合理分配。綜上所述，本文模型能在注入相同噪聲的情況下獲得最好的感知質量和最低的PSNR值，性能優于其他3個JND模型。

4 結束語

本文通過探索HVS主動預測輸入信號的特性，提出基于熵掩蔽的DCT域JND模型。算法充分考慮DCT塊間的相關性，設計基于紋理能量相似性的DCT域貝葉斯預測模型，利用預測殘差計算塊級無序度描述圖像內容的不確定性；最終將熵掩蔽效應構建為關于無序度的調節因子，以指示更多噪聲分配到包含大量不確定信息的無序紋理區域。主觀、客觀實驗結果表明，所提模型能在避免跨域操作的同時去除更多感知冗余，性能優于現有JND模型。

[1] JAYANT N, JOHNSTON J, SAFRANEK R. Signal compression based on models of human perception[J]. Proceedings of the IEEE, 1993, 81(10): 1385-1422.

[2] KI S, DO J, KIM M. Learning-based JND-directed HDR video preprocessing for perceptually lossless compression with HEVC[J]. IEEE Access, 2020(8): 228605-228618.

[3] 崔帥南, 彭宗舉, 鄒文輝, 等. 多特征融合的合成視點立體圖像質量評價[J]. 電信科學, 2019, 35(5): 104-112.

CUI S N, PENG Z J, ZOU W H, et al. Quality assessment of synthetic viewpoint stereo image with multi-feature fusion[J]. Telecommunications Science, 2019, 35(5): 104-112.

[4] LI J, ZHANG H, WANG J, et al. Orientation-aware saliency guided JND model for robust image watermarking[J]. IEEE Access, 2019(7):41261-41272.

[5] XU Y F, ZHANG N, LI L, et al. Joint learning of super-resolution and perceptual image enhancement for single image[J]. IEEE Access, 2021(9):48446-48461.

[6] 邢亞芬, 殷海兵, 王鴻奎, 等. 基于視頻時域感知特性的恰可察覺失真模型[J]. 電信科學, 2022, 38(2): 92-102.

XING Y F, YIN H B, WANG H K, et al. Video temporal perception characteristics based just noticeable difference model[J]. Telecommunications Science, 2022, 38(2): 92-102.

[7] BAE S H, KIM M. A novel generalized DCT-based JND profile based on an elaborate CM-JND model for variable block-sized transforms in monochrome images[J]. IEEE Transactions on Image Processing, 2014, 23(8): 3227-3240.

[8] FRISTON K J, DAUNIZEAU J, KIEBEL S J. Reinforcement learning or active inference?[J]. PloS one, 2009, 4(7): e6421.

[9] FRISTON K. The free-energy principle: a unified brain theory?[J]. Nature Reviews Neuroscience, 2010, 11(2): 127-138.

[10] WU J J, SHI G M, LIN W S, et al. Just noticeable difference estimation for images with free-energy principle[J]. IEEE Transactions on Multimedia, 2013, 15(7): 1705-1710.

[11] WU J J, LI L D, DONG W S, et al. Enhanced just noticeable difference model for images with pattern complexity[J]. IEEE Transactions on Image Processing, 2017, 26(6): 2682-2693.

[12] ZENG Z P, ZENG H Q, CHEN J, et al. Visual attention guide dpixel-wise just noticeable difference model[J]. IEEE Access, 2019(7): 132111-132119.

[13] LIU X Q, ZHAN X N, WANG M H. A novel edge-pattern-based just noticeable difference model for screen content images[C]//2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP). Piscataway: IEEE Press, 2020: 386-390.

[14] WANG H K, YU L, LIANG J H, et al. Hierarchical predictive coding-based JND estimation for image compression[J]. IEEE Transactions on Image Processing, 2020(30): 487-500.

[15] WATSON A B. DC Tune: A technique for visual optimization of DCT quantization matrices for individual images[C]//Sid International Symposium Digest of Technical Papers, Society for Information Display, 1993(24): 946-946.

[16] WEI Z Y, NGAN K N. Spatio-temporal just noticeable distortion profile for grey scale image/video in DCT domain[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2009, 19(3): 337-346.

[17] ECKERT M P, BRADLEY A P. Perceptual quality metrics applied to still image compression[J]. Signal processing, 1998, 70(3): 177-200.

[18] ZHANG X H, LIN W S, XUE P. Improved estimation for just-noticeable visual distortion[J]. Signal Processing, 2005, 85(4): 795-808.

[19] KNILL D C, POUGET A. The Bayesian brain: the role of uncertainty in neural coding and computation[J]. TRENDS in Neurosciences, 2004, 27(12): 712-719.

[20] EASTTOM C. On the use of the SSIM algorithm for detecting intellectual property copying in web design[C]//2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC). Piscataway: IEEE Press: 2021: 0860-0864.

[21] Le C P, Autrusseau F. Subjective quality assessment IRCCyN/IVC database[EB]. 2005.

[22] Ponomarenko N, Jin L, Ieremeiev O, et al. Image database TID2013: peculiarities, results and perspectives[J]. Signal Processing: Image Communication, 2015, 30: 57-77.

[23] JUDD T, EHINGER K, DURAND F, et al. Learning to predict where humans look[C]//2009 IEEE 12th International Conference on Computer Vision. Piscataway: IEEE Press, 2009: 2106-2113.

[24] WANG H K, YU L, YIN H B, et al. An improved DCT-based JND estimation model considering multiple masking effects[J]. Journal of Visual Communication and Image Representation, 2020(71): 102850.

[25] LI J L, YU L, WANG H K. Perceptual redundancy model for compression of screen content videos[J]. IET Image Processing, 2022, 16(6): 1724-1741.

[26] WANG J, LIU Y, WEI P, et al. Fractal image coding using SSIM[C]//2011 18th IEEE International Conference on Image Processing. Piscataway: IEEE Press, 2011: 241-244.

Just noticeable distortion model based on entropy masking in DCT domain

LUO Qionghua, WANG Hongkui, YIN Haibing, XING Yafen

College of Communication Engineering, Hangzhou Dianzi University, Hangzhou 310018, China

In order to improve the threshold accuracy of JND (just noticeable distortion) model in DCT (discrete cosine transform) domain and avoid cross-domain operation, entropy masking effect was introduced into DCT-based JND model. Firstly, starting from the free-energy theory and the Bayesian inference, an autoregressive model based on texture-energy similarity in DCT domain was designed to simulate the spontaneous prediction behavior of visual perception. Secondly, the mapping relationship between visual perception and prediction residuals were explored to obtain the disorder intensity in block level. Thirdly, the entropy masking effect was modeled as a JND threshold modulation factor of disorder intensity. Finally, the JND model in DCT domain for the entropy masking was proposed by fusing the contrast sensitivity function, the luminance adaptive masking, the contrast masking. Compared with the existing JND model in DCT domain, the proposed model performed all operations in DCT domain, which was more efficient and concise. The subjective and objective experimental results indicate that the proposed JND model shows greater tolerance to distortion with better perceptual quality.

JND, human visual system, entropy masking effect, free-energy theory, Bayesian inference

TN91

A

10.11959/j.issn.1000–0801.2023014

駱瓊華（1998-），女，杭州電子科技大學通信工程學院碩士生，主要研究方向為視頻感知編碼。

王鴻奎（1990-），男，博士，杭州電子科技大學通信工程學院講師，主要研究方向為視覺感知理論、視頻感知編碼以及視頻智能編碼。

殷海兵（1974-），男，博士，杭州電子科技大學通信工程學院教授，主要研究方向為數字視頻編解碼、圖像和視頻處理以及VLSI結構設計。

邢亞芬（1997-），女，杭州電子科技大學通信工程學院碩士生，主要研究方向為視頻感知編碼。

The National Natural Science Foundation of China (No.62202134, No.61972123, No.61931008, No.62031009), Zhejiang Provincial “Pioneer” and “Leading Goose”Research and Development Project (No.2023C01149, No.2022C01068)

2022-08-03；

2023-01-09

國家自然科學基金資助項目（No.62202134，No.61972123，No.61931008，No.62031009）；浙江省“尖兵”“領雁”研發攻關計劃項目（No.2023C01149，No.2022C01068）