非正弦激勵下納米晶材料高頻磁心損耗的計算方法改進與驗證

劉 歡 李永建 張長庚 穆生輝 金楚皓

非正弦激勵下納米晶材料高頻磁心損耗的計算方法改進與驗證

劉 歡 李永建 張長庚 穆生輝 金楚皓

（河北工業大學省部共建電工裝備可靠性與智能化國家重點實驗室 天津 300130）

軟磁材料廣泛應用于各種電氣設備的鐵心，磁心損耗的精確計算關系著電氣設備的效率。尤其是高頻非正弦激勵條件下磁心損耗的精確計算，是逆變器、電力電子變壓器和高頻電抗器等電力電子裝置的優化設計的重要組成部分。該文首先總結了幾種非正弦激勵下的磁心損耗的計算方法，對比幾種改進的Steinmetz經驗公式，分析磁化過程對磁心損耗的影響；然后提出一種考慮磁感應強度變化率的改進Steinmetz波形系數公式（WcSE）計算模型，推導出高頻方波和矩形波激勵下的損耗計算表達式；接著搭建高頻非正弦激勵下的軟磁材料磁特性測試系統，在頻率為10～70kHz范圍內對環形納米晶樣品（FT-3KL和FT-3KS）進行不同占空比的方波和矩形波激勵下的高頻磁特性實驗，得到方波和矩形波激勵下的磁心損耗實驗測量值；最后對比實驗值和幾種修正Steinmetz模型的計算值，并進行誤差分析，得到改進的WcSE計算模型的平均計算誤差在20%以內，均小于Steinmetz修正公式、修正廣義Steinmetz公式和WcSE的計算誤差的結論，驗證了所提改進的WcSE新模型的計算精確性，為電力電子裝置的磁心損耗預測以及優化設計提供了重要依據。

納米晶 磁心損耗 非正弦激勵 Steinmetz經驗公式

0 引言

隨著電力電子技術的快速發展以及智能電網和能源互聯網發展的需要，磁性元件在逆變器、固態變壓器、開關電源等電力電子裝置中得到了廣泛的應用[1-4]。磁心損耗是電力電子裝置總損耗的重要組成部分，也是影響電力電子裝置小型化和高頻化的重要因素[5]。然而，電力電子裝置中磁心的激勵波形一般是非正弦波，工作頻率可達數kHz甚至數百kHz，且含有大量諧波[6]。磁心損耗約占總損耗的30%，且隨著工作頻率的提高而顯著增加，對裝置的可靠性和使用壽命會產生影響[7]。因此，研究高頻非正弦激勵下的磁心損耗，對提高整機的效率和功率密度具有重要意義。

方波是典型的中頻變壓器端口電壓波形，具有半橋拓撲結構的開關變換器磁心往往承受方波電壓激勵，高頻變壓器的激勵源波形也主要為方波；在永磁無刷直流電機和變頻器中，磁心主要承受矩形波激勵，在功率變換器應用中，磁性元件通常工作在矩形波信號激勵之下[8-12]。因此研究方波和矩形波產生的磁心損耗就成為一個迫切需要解決的問題。近年來，學術界進行了大量的工作來研究方波、矩形波乃至任意波形激勵下的磁心損耗問題。然而，非正弦情況下的鐵心損耗預測模型仍然非常少見。文中針對方波和矩形波這兩種應用廣泛的非正弦波形進行了推導。

目前計算正弦激勵下磁心損耗的方法主要有磁滯模型法、經驗公式法和損耗分離法。磁滯模型法由于其需要大量的計算參數而不適用于工程實際，因此在實際工程中一般采用經驗公式法和損耗分離法。非正弦激勵下的損耗計算是基于上述兩種方法的改進和修正。文獻[9]研究了幾種Steinmetz經驗公式，并針對復合波形的特點提出新的損耗計算方法，但其損耗計算精度過度依賴Steinmetz波形系數公式的計算精度，并不適合其他波形激勵的損耗預測。文獻[10,13-16]分別推導了方波、矩形波、三角波等非正弦激勵下的Steinmetz經驗公式，并對比分析了常用非正弦激勵損耗計算方法的精度，在一定程度上對Steinmetz經驗公式中的參數進行修正，針對特定材料特定頻率下的損耗計算公式的精確度得到改進。文獻[17]針對損耗分離公式，建立考慮趨膚效應的渦流損耗模型，提高了計算精度。但其頻率限制在20kHz以內，只是在仿真的基礎上實現了預測，并沒有用于實驗驗證。文獻[11]從另一角度出發，利用無直流偏磁脈沖寬度調制（Pulse Width Modulation, PWM）波勵磁的磁心損耗模型推導出直流偏磁下PWM波勵磁的磁心損耗。該方法只適用于PWM波，并不能推廣于其他非正弦激勵。文獻[12]分析了開關電源變換器中的鐵氧體磁心損耗，提出關于電阻率與渦流損耗的計算方法，實現了鐵氧體材料的非正弦損耗預測，但對其他磁性材料不再適用。

本文針對Steinmetz經驗公式中影響磁心損耗的關鍵因素，推導了一種新的非正弦激勵下磁心損耗計算模型，實現了高頻非正弦激勵下的磁心損耗預測。搭建基于碳化硅全橋逆變電路的高頻非正弦激勵磁特性測試平臺，通過測量納米晶磁環在正弦和非正弦激勵下不同磁通密度和不同頻率時的磁心損耗，獲得其Steinmetz經驗公式擬合參數，得到非正弦損耗計算解析式，并與非正弦損耗結果進行比較，驗證了非正弦激勵下磁心損耗模型的準確性。對兩種不同型號的納米晶材料進行了對比分析，進一步驗證了新公式的準確性和普適性。

1 磁心損耗計算方法

1.1 Steinmetz經驗公式

Steinmetz經驗公式（Original Steinmetz Equation, OSE）是C. P. Steinmetz在1892年提出的，認為磁心損耗與頻率和磁通密度峰值有關，即

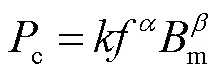
式中，為激勵電壓頻率，Hz；m為磁通密度峰值，T；、、均為在正弦激勵下的Steinmetz參數，其值與磁性材料種類、勵磁頻率和磁感應強度幅值有關。

1.2 Steinmetz修正公式

上述方法僅適用于正弦波形，然而，大多數電力電子裝置輸出的波形通常是非正弦的，其計算精度在非正弦激勵下會變得很差。

因此，為了克服上述問題，引入Steinmetz修正公式（Modified Steinmetz Equation, MSE）。MSE適用于非正弦激勵下的磁心損耗預測。MSE引入了磁感應強度變化率（d/d），認為磁心損耗除了與磁化過程中的磁感應強度峰峰值D有關之外，還與磁感應強度變化率（d/d）直接相關。MSE將SE當中的頻率用一個等效頻率來代替，eq是根據平均再磁化率計算出的等效頻率，其表達式為

式中，D為一個磁化周期內磁感應強度的峰峰值，D=max-min，max、min分別為一個磁化周期內磁感應強度的最大值和最小值。將等效頻率代入SE中得到MSE修正公式為

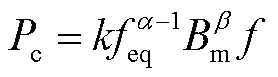
1.3 廣義Steinmetz公式

為了克服MSE在正弦激勵下的磁心損耗計算存在偏差這一問題，Li Jieli等推導得到了廣義Steinmetz公式（Generalized Steinmetz Equation, GSE），其目標是將MSE置于Steinmetz方法形式并克服MSE的限制。廣義Steinmetz公式認為磁心損耗不僅與磁感應強度變化率有關，還與磁感應強度的瞬時值有關，它用磁感應強度瞬時值和磁感應強度變化率來代替最大磁通密度，其表達式為

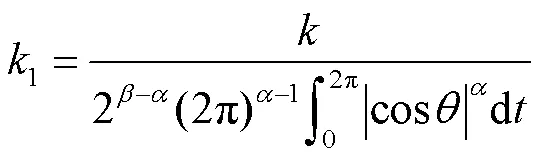
1.4 修正廣義Steinmetz公式

GSE體現了磁心損耗與磁感應強度變化率及磁感應強度的瞬時值的關系，但是磁性材料的磁化過程還和磁化歷史有關，因此，考慮到磁化過程的影響，修正廣義Steinmetz公式（Improved Generalized Steinmetz Equation, IGSE），將GSE中的磁感應強度瞬時值替換為磁感應強度的峰峰值D，其表達式為

對于分段線性的波形來說，IGSE的計算簡單方便，這是因為式（6）中的積分可以被簡單的總和代替，所以IGSE最精確，并且這種方法既考慮了主磁滯回線也考慮了小磁滯回環。它比前面提到的修正方法具有更好的準確性。但是，它沒有考慮直流偏置的影響[18]。

1.5 Steinmetz波形系數公式

Steinmetz波形系數公式（Waveform coefficient Steinmetz Equation, WcSE）定義了波形系數，即不同激勵下一個磁化周期內磁感應強度曲線與坐標軸所包圍的面積與正弦下的比值，其表達式為

綜上所述，Steinmetz修正公式從不同層面考慮了非正弦激勵與正弦激勵磁化過程的區別，主要表現在磁感應強度變化率d/d、磁感應強度瞬時值()和一個磁化周期內磁感應強度變化峰峰值D，這些變量的引入在不同程度上提高了修正公式對損耗的預測精確度。

磁心損耗特性由其磁化過程決定，磁化曲線能描述磁環的磁化過程[15]。在以上修正公式中，WcSE是以磁感應強度曲線為基礎預測磁心損耗，因此WcSE從原理上優于其他修正公式。

2 高頻非正弦磁心損耗模型

2.1 基于經驗公式的分析及修正

軟磁材料的磁化過程十分復雜，且隨激勵增大呈現非線性關系，非正弦激勵會帶來大量的諧波，使軟磁材料的磁化特性的非線性加劇，造成物理建模困難。文獻[10]對比了第1節中幾種修正公式的精度，得到以下結論：在不同占空比的方波和矩形波激勵下，SE的預測精確度最差，IGSE的精確度最好，MSE介于前兩種之間；當占空比為0.5時，WcSE的精確度很好，超過IGSE，但在其他占空比時精確度會變差。然而IGSE的參數辨識過于復雜，MSE的精確度不高，計算式簡單的WcSE在其他占空比下精確度又太差。因此，需要一種結構簡單且精度高的經驗公式以解決非正弦激勵磁心損耗預測難題。

文獻[9]中提到主要影響磁心損耗計算精度的因素是磁感應強度瞬時值()和磁感應強度變化率d/d。WcSE在非正弦激勵時其他占空比的精確度會變差的原因是WcSE通過求解磁感應強度曲線與坐標軸所包圍的面積計算損耗，忽視了磁感應強度變化率對鐵磁材料的磁特性的影響造成的損耗。因此在WcSE的基礎上，引入磁感應強度變化率，得到改進的WcSE公式（Improved Waveform coefficient Steinmetz Equation, IWcSE），引進參數表達式為

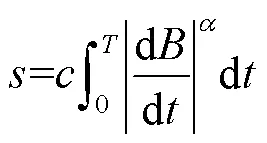
式中，為改進系數。通過推導特定非正弦激勵如方波、矩形波可以得到IWcSE的表達式。

方波激勵波形及對應磁通密度波形如圖1所示。

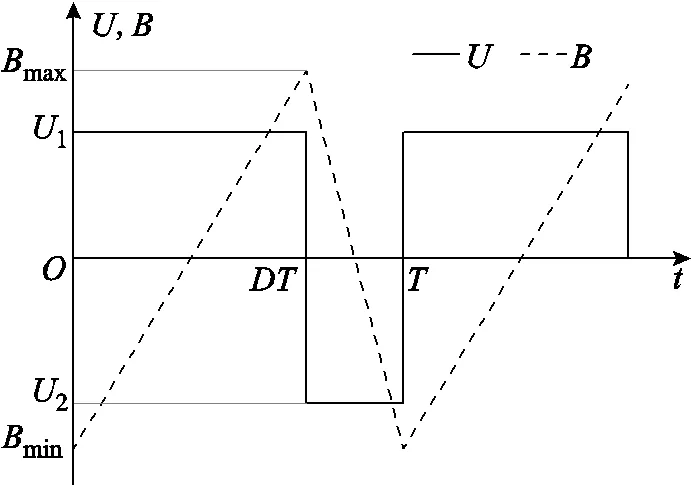
圖1 方波激勵波形及對應磁通密度波形

不同占空比的方波在一個函數周期內的表達式為

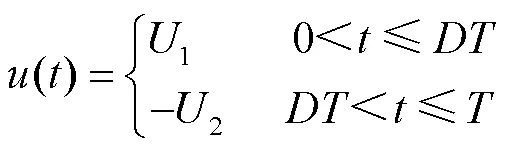
其在一個周期內磁感應強度變化率的表達式為

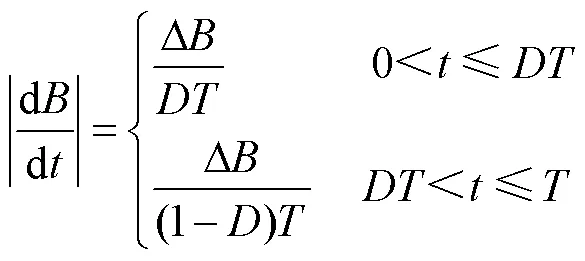
將式（11）代入式（9）可得IWcSE的參數表達式為

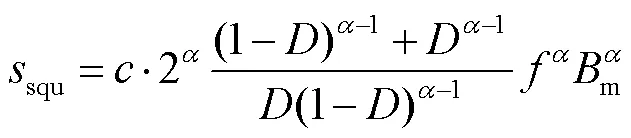
從式（12）可以看出不同占空比的方波激勵下磁感應強度變化率對損耗的影響體現在占空比和磁感應強度峰值上，且僅用正弦激勵下的參數來描述磁感應強度峰值對損耗的影響，已經不能滿足其精度的要求，因此認為磁感應強度變化率d/d對損耗也有貢獻，不能忽略。另外，對磁感應強度峰值也有貢獻。考慮到WcSE已經將頻率和磁感應峰值考慮進去，所以可以得到IWcSE的表達式為

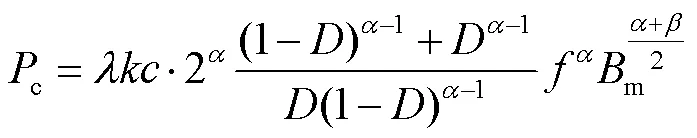
矩形波激勵波形及對應磁通密度波形如圖2所示。

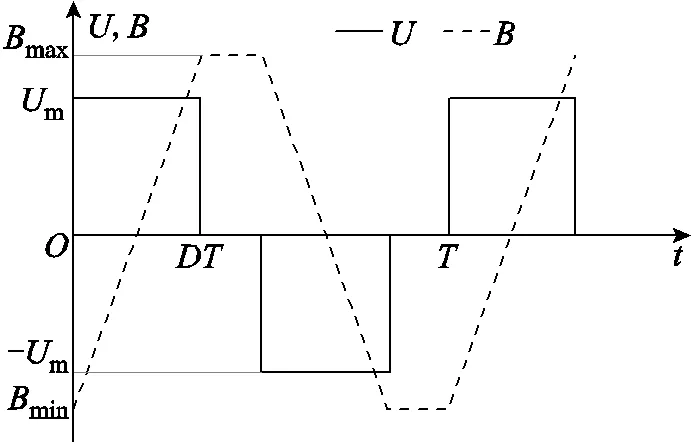
圖2 矩形波激勵波形及對應磁通密度波形

不同占空比的矩形波在一個函數內的表達式為

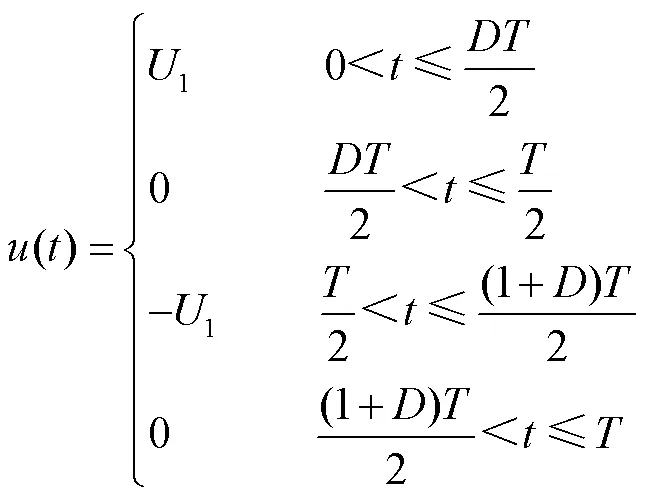
其在一個周期內磁感應強度變化率的表達式為

將式（15）代入式（9）可得改進的WcSE的參數表達式為

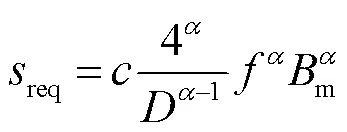
IWcSE的表達式為

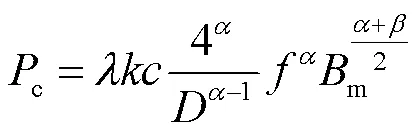
WcSE關于方波的波形系數squ和矩形波的波形系數req分別為

將式（11）和式（15）代入式（3）、式（4）、式（6）得到方波和矩形波激勵下的MSE、IGSE、WcSE公式，見表1。

表1 非正弦激勵下的損耗計算式

Tab.1 Loss calculation in non-sinusoidal excitation

2.2 基于實驗測量的鐵耗計算解析式

為了獲得上述Steinmetz經驗修正公式的解析式，對環形納米晶磁心進行正弦實驗。采用實驗室軟磁材料交流磁特性測試系統，分別測試了環形納米晶FT-3KL和FT-3KS在正弦激勵下不同磁通密度（0.1～1.1T）和不同頻率（5～20kHz）時的磁心損耗。納米晶FT-3KL尺寸為外徑41mm，內徑25mm，高度15mm，磁心為帶繞，疊片厚度0.02mm；FT-3KS尺寸為外徑40mm，內徑32mm，高度15mm，磁心為帶繞，疊片厚度為0.02mm。

圖3為正弦激勵下納米晶FT-3KL的動態磁滯回線。對環形納米晶在正弦激勵下的磁心損耗測量值進行擬合，得到Steinmetz經驗公式的參數見表2。將這些參數代入表1的公式中就可以得到方波和矩形波激勵下不同修正公式的解析計算式。

圖3 正弦波激勵下的動態磁滯回線

表2 Steinmetz經驗公式擬合參數

Tab.2 Steinmetz empirical formula parameters

3 非正弦激勵磁心損耗測量及驗證

3.1 實驗平臺的搭建

本文搭建了如圖4所示的非正弦高頻磁環動態磁特性測試系統。非正弦激勵信號如不同占空比的方波和矩形波由直流源經過DSP控制逆變電路產生，碳化硅全橋逆變電路可輸出幾十到幾百kHz頻率的方波和矩形波。電路中隔直電容可以消除激勵電源的直流分量，避免偏磁，還可以維持波形的平直。測試實驗平臺如圖5所示。

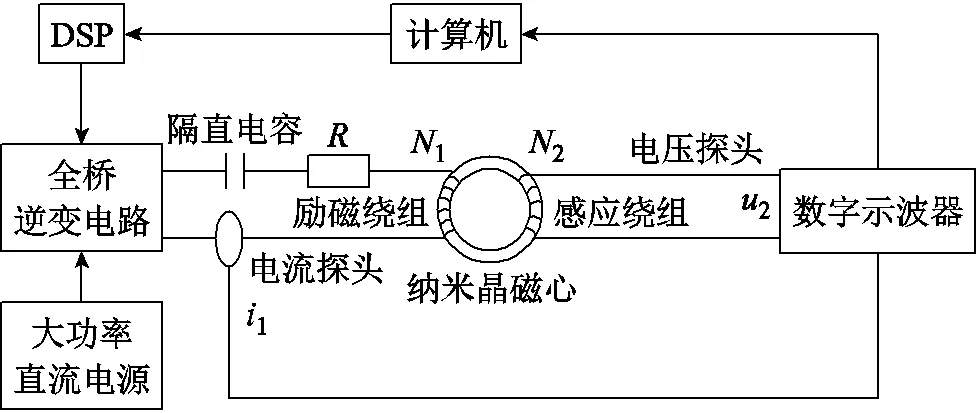
圖4 非正弦實驗測量系統

圖5 測試實驗平臺

通過電壓探頭和電流探頭采集一次電流1()和二次電壓2()的波形數據，通過式（20）和式（21）獲得磁環的動態磁滯回線，通過式（22）獲得磁環的磁心損耗。

式中，1為一次側匝數；2為二次側匝數；為磁心的橫截面積；為磁心的有效磁路長度。

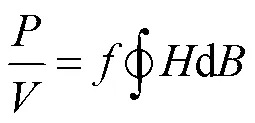
利用圖4所示非正弦測試系統對納米晶FT-3KL和FT-3KS進行空載實驗，測量它們的磁心損耗。利用DSP軟件程序控制逆變電路輸出不同占空比值（=0.1～0.9），頻率范圍為10～70kHz，磁通密度范圍為0.1～1.1T的方波和矩形波，同時，計算機可以實時讀取一次電流和二次電壓實際值，獲得實驗數據。

3.2 非正弦激勵下Steinmetz修正公式對比

通過正弦實驗可以得到經驗公式參數，代入表1就可以得到修正公式的計算式，對于IWcSE中的參數，通過計算值與實驗值擬合，可得= 0.1。將環形納米晶磁心FT-3KL和FT-3KS分別在方波和矩形波的激勵下的損耗測量結果和修正公式的損耗預測計算結果進行對比，以驗證IWcSE的計算精度。

FT-3KL在方波激勵下的損耗對比結果如圖6和圖7所示。圖6為FT-3KL在30kHz和=0.1時不同磁通密度下的損耗對比，圖7為FT-3KL在70kHz和m=0.5T時不同占空比時的損耗對比。從圖6可以看出，MSE和IGSE在高磁通密度（0.7T以上）的計算值與實驗測量值比較接近，但是在低磁通密度下的計算值與測量值相差很大。同時也可以發現MSE和IGSE對方波損耗的預測計算值十分接近，這也從側面反映了MSE和IGSE對于高頻情況下的非正弦損耗預測已經不再具有良好的精確度；而整體上WcSE的計算值與測量值相差很大，精確度小于MSE和IGSE。因此，針對頻率在20kHz以上的非正弦損耗預測公式，MSE、IGSE及WcSE都不具備良好的計算精度。對于IWcSE，在整個磁通密度區間其計算值與測量值相差很小，這說明在進行非正弦損耗預測時，不能為了迎合原始的Steinmetz經驗公式的形式而忽視d/d對m的影響。

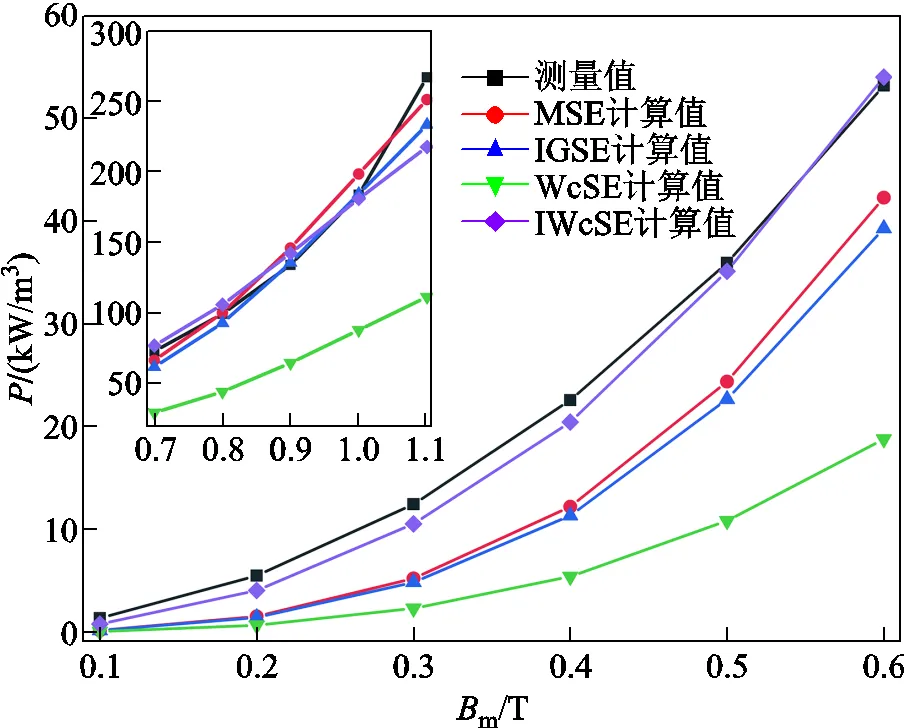
圖6 FT-3KL在30kHz和D=0.1時方波激勵下損耗結果對比

圖7 FT-3KL在70kHz和Bm=0.5T時方波激勵下損耗結果對比

從圖7可以看出，對于不同的占空比來說，方波激勵下的損耗隨著占空比的變化呈現U型分布，且占空比越趨近于0.5，所含諧波成分越少，磁心損耗也就越小。IWcSE通過引入磁感應強度變化率克服了WcSE與占空比無關的缺陷，使預測結果與實際測量結果相吻合，由此可以驗證IWcSE對于方波激勵下磁心損耗預測的準確性。

矩形波激勵下的損耗對比結果如圖8和圖9所示。圖8為FT-3KL在70kHz和=0.5時不同磁通密度下的損耗對比，圖9為FT-3KL在50kHz和m=0.3T時不同占空比時的損耗對比。從圖8可以看出，隨著磁通密度的增加，MSE、IGSE以及WcSE對于磁心損耗的計算精度在不斷下降，與方波不同的是，MSE和IGSE的計算值不再相近，它們的趨勢向兩個不同的方向發展：MSE對矩形波激勵下的磁心損耗計算值比實驗值偏大，且隨著磁通密度的增加，上升幅度持續增大；而IGSE對矩形波激勵下的磁心損耗計算值比實驗值偏小。而IWcSE的計算值與測量值的誤差很小，其精度優于上述三種方法。

從圖9可以看出，矩形波激勵下的損耗隨著占空比的增大而減小，線性度要比方波激勵下損耗線性度好。且當占空比趨近于1時，矩形波就轉換為占空比為0.5的方波；當占空比趨近于0.1時，矩形波的帶寬就會非常小。此時，波形攜帶的諧波含量較大，容易使磁通波形產生畸變，造成損耗的急劇增加。對于不同修正公式的精確度來說，MSE、IGSE及WcSE的損耗計算值與測量值的差值隨著占空比的減小而增大，而IWcSE的計算值與測量值相差很小，其精度受到占空比的影響小，具有良好的穩定性，其預測結果均優于其他修正公式。因此，IWcSE適用于不同非正弦激勵波形下的磁心損耗預測，并具有良好的計算精度。

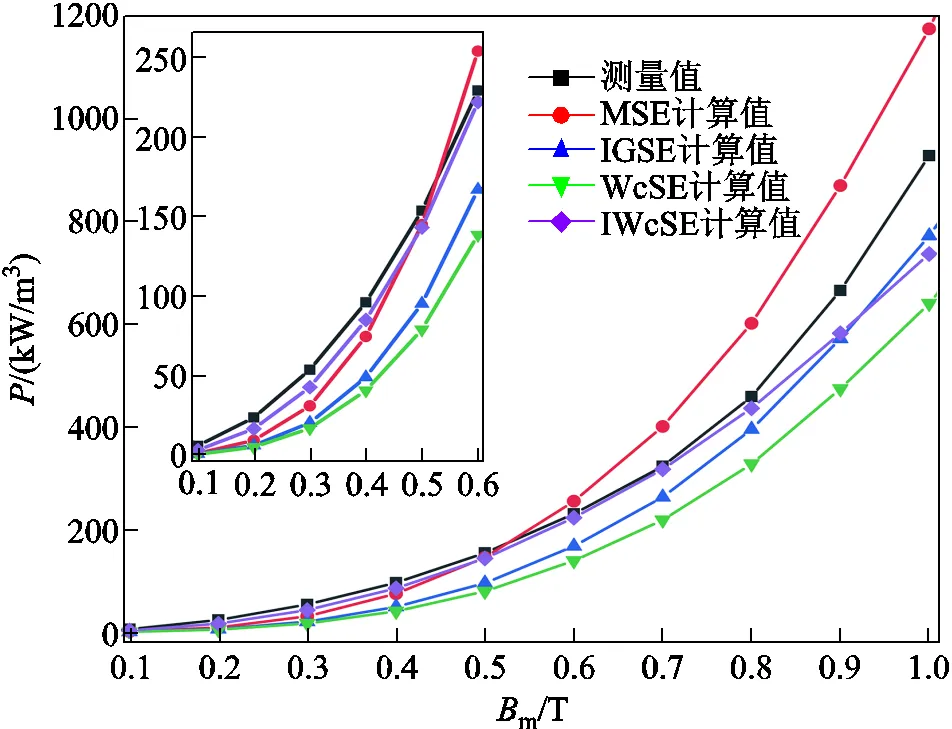
圖8 FT-3KL在70kHz和D=0.5時矩形波激勵下損耗結果對比

圖9 FT-3KL在50kHz和Bm=0.3T時矩形波激勵下損耗結果對比

FT-3KS在方波激勵下的損耗對比結果如圖10和圖11所示。圖10為FT-3KS在30kHz和=0.3時不同磁通密度下的損耗對比，圖11為FT-3KS在70kHz和m=0.5T時不同占空比時的損耗對比。從圖10可以看出，與FT-3KL的規律相同，IWcSE的精確度優于MSE、IGSE和WcSE，且在磁通密度較低時，其計算值與實驗測量值基本一致。從圖11也可以得到相同的結論，IWcSE能夠反映磁心損耗隨占空比非線性變化的趨勢，并且具有良好的精度，驗證了此方法適用于不同的納米晶材料。

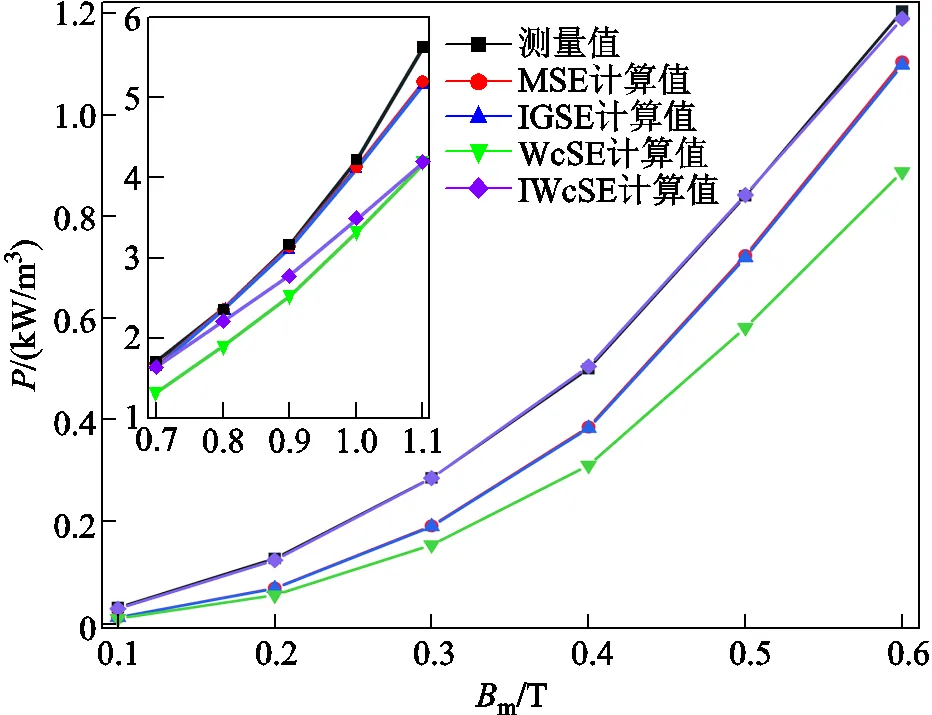
圖10 FT-3KS在30kHz和D=0.3時方波激勵下損耗結果對比

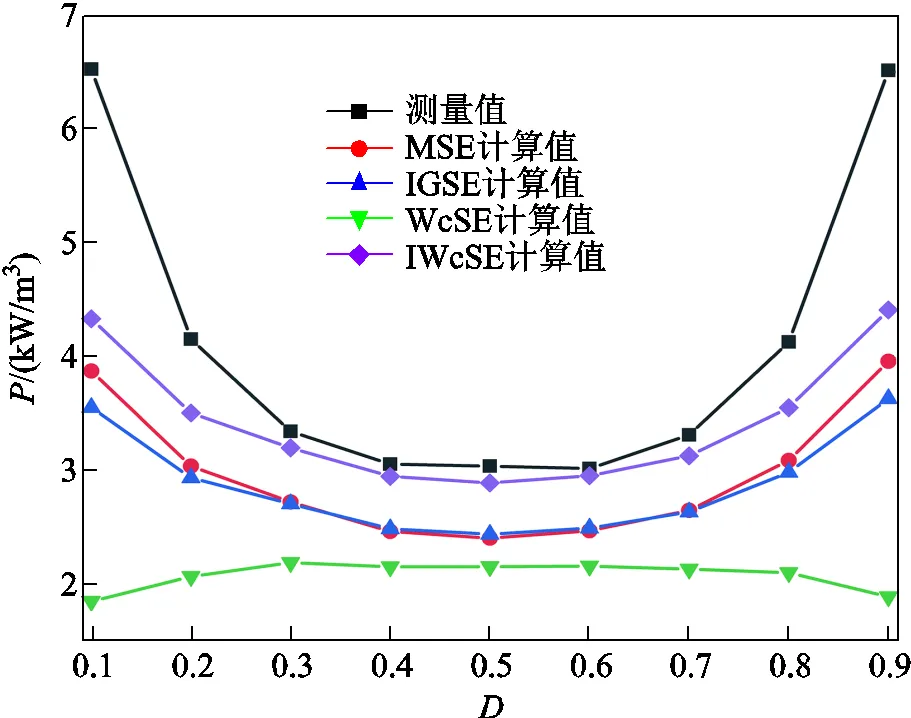
圖11 FT-3KS在70kHz和Bm =0.5T時方波激勵下損耗結果對比

同理，FT-3KS在矩形波激勵下的損耗對比結果如圖12和圖13所示。圖12為FT-3KS在70kHz和=0.3時不同磁通密度下的損耗對比，圖13為FT-3KS在70kHz和m=0.3T時不同占空比時的損耗對比。其結果與FT-3KL在矩形波激勵下磁心損耗的分析結果一致，均符合上述規律，從而驗證了IWcSE對納米晶材料的普適性。

對于極端情況下，如過飽和以及占空比趨近于0.1和0.9時，磁滯回線處于強非線性階段，磁環所受激勵中諧波含量劇增，引起的發熱會造成磁環的熱退磁現象，這樣會加重磁環的過飽和，造成損耗急劇增加。此時，IWcSE模型預測磁心損耗的精度會降低。

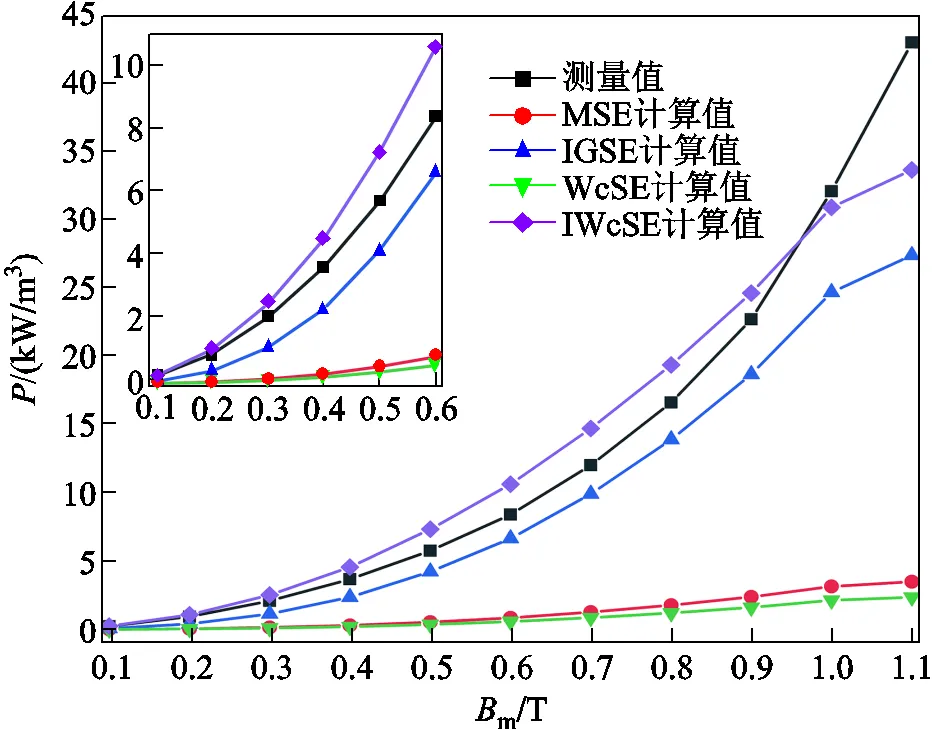
圖12 FT-3KS在70kHz和D=0.3時矩形波激勵下損耗結果對比

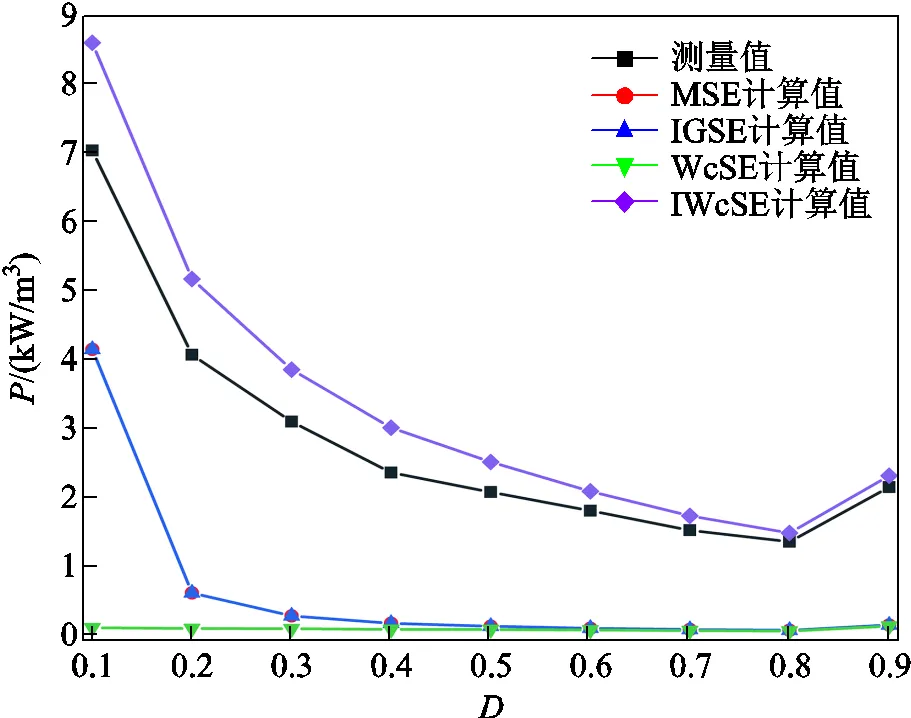
圖13 FT-3KS在70kHz和Bm=0.3T時矩形波激勵下損耗結果對比

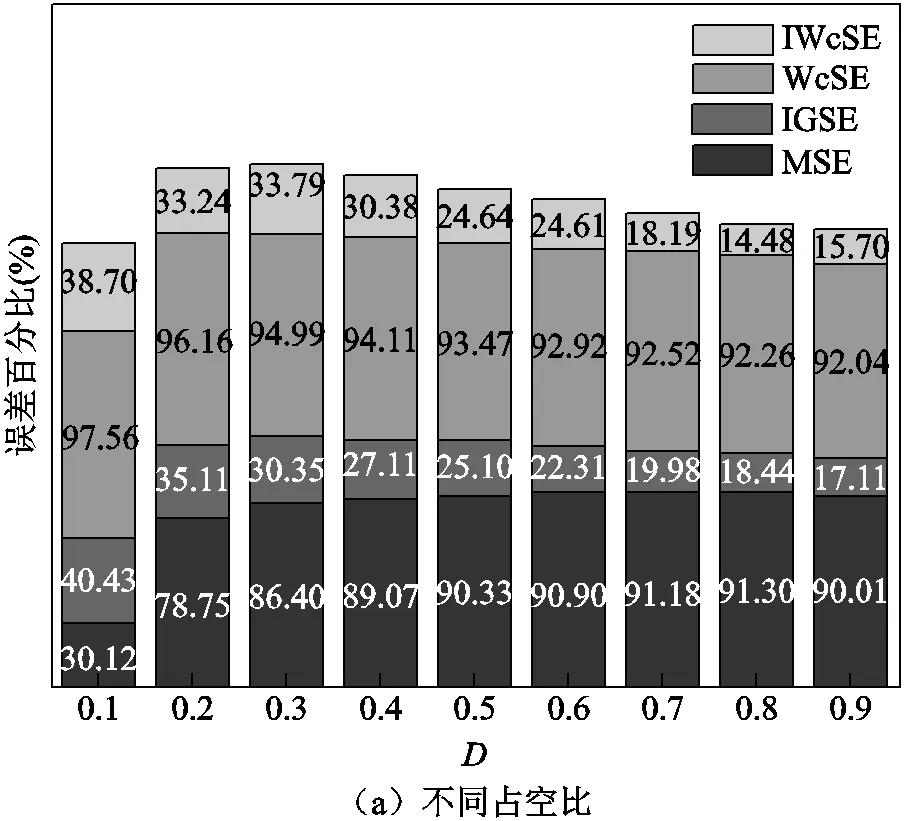
為了進一步驗證IWcSE的計算精度，分別將MSE、IGSE、WcSE和IWcSE在不同頻率、不同磁通密度和不同占空比的計算值與實驗測量值進行誤差對比，對比結果如圖14～圖17所示。圖14和圖15分別為FT-3KL在方波和矩形波激勵下各種修正公式的計算平均誤差對比，圖16和圖17分別為FT-3KS在方波和矩形波激勵下各種修正公式的計算平均誤差對比。從圖中可以看出：WcSE的平均誤差最大、MSE較大、IGSE次之、IWcSE最小，并且IWcSE的平均誤差均在20%以下，在不同占空比和不同頻率下具有較好的穩定性，驗證了此改進公式的普遍適用性和計算準確性。

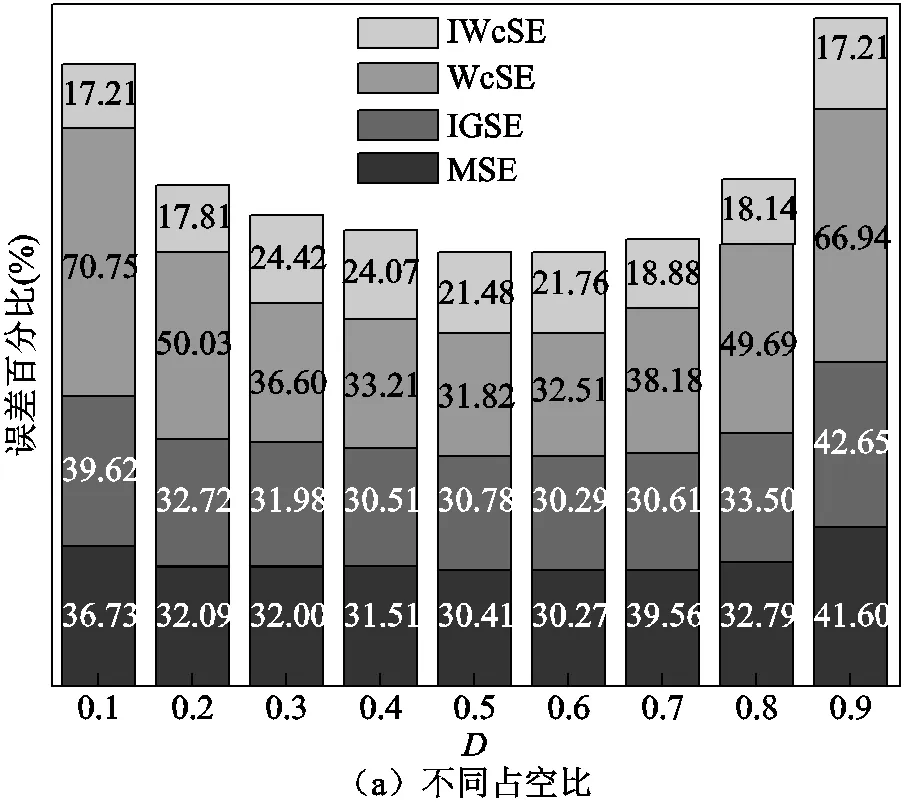
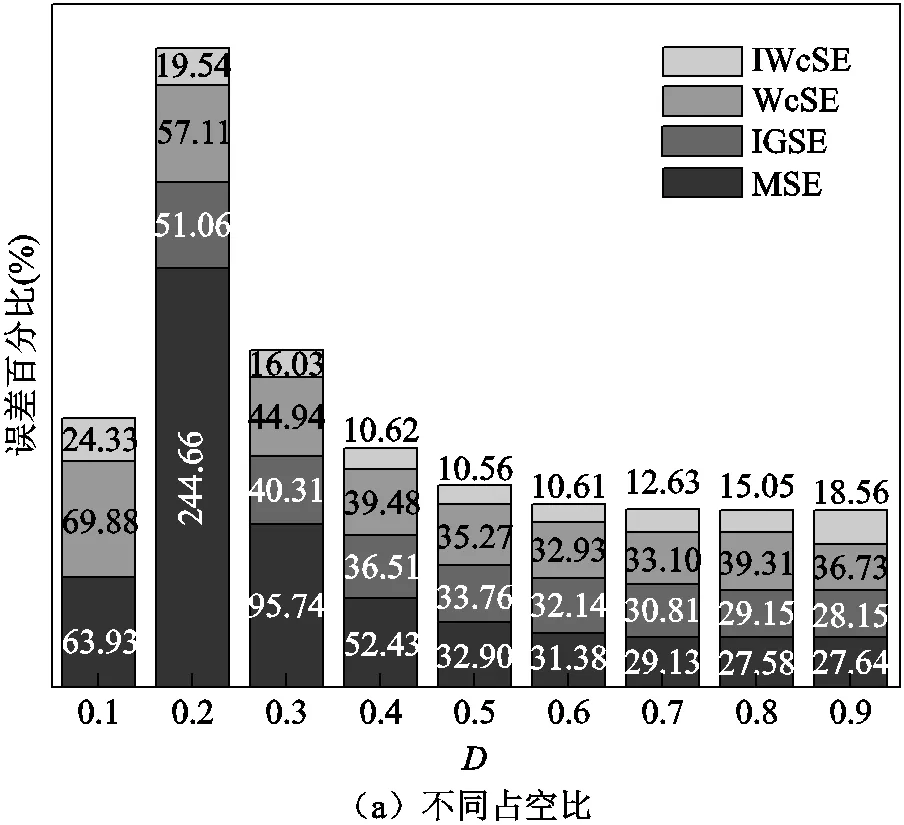
圖16 FT-3KS在方波激勵下的損耗誤差對比

4 結論

1）本文對比了各種非正弦修正經驗公式，從損耗原理出發，考慮了d/d對損耗的影響，推導出一種改進的WcSE的修正公式的高頻非正弦磁心損耗計算模型。

2）搭建了高頻非正弦激勵軟磁材料的磁特性測試系統，對比分析了幾種經驗公式以及新的計算模型的計算值與實驗測量結果，并做了誤差分析，驗證了本文給出的IWcSE公式的準確性和實用性。

[1] 王寧, 張建忠. 基于開關軌跡優化的 SiC MOSFET 有源驅動電路研究綜述[J].電工技術學報, 2022, 37(10): 2523-2537. Wang Ning, Zhang Jianzhong. Review of active gate driver for SiC MOSFET with switching trajectory optimization[J]. Transactions of China ElectrotechnicalSociety, 2022, 37(10): 2523-2537.

[2] 黃華震, 仝涵, 王寧燕, 等. 考慮寄生振蕩的IGBT分段暫態模型對電磁干擾預測的影響分析[J]. 電工技術學報, 2021, 36(12): 2435-2445. Huang Huazhen, Tong Han, Wang Ningyan, et al. Analysis of the influence of IGBT segmented transient model with parasitic oscillation on electromagnetic interference prediction[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2435-2445.

[3] 凌亞濤, 趙爭鳴, 姬世奇. 基于主動柵極驅動的IGBT開關特性自調節控制[J]. 電工技術學報, 2021, 36(12): 2483-2494. Ling Yatao, Zhao Zhengming, Ji Shiqi. Self-regulating control of IGBT switching characteristics with active gate drive[J]. Transactions of China Electrotechnical Society, 2021, 36(12): 2483-2494.

[4] 李子欣, 高范強, 趙聰, 等. 電力電子變壓器技術研究綜述[J]. 中國電機工程學報, 2018, 38(5): 1274-1289. Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer technologies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.

[5] 關金萍, 徐永海. 電力電子變壓器在風力發電系統中的應用研究綜述[J]. 電工電能新技術, 2019, 38(2): 88-96. Guan Jinping, Xu Yonghai. Research review of power electronic transformer applications in wind energy conversion systems[J]. Advanced Technology of Electrical Engineering and Energy, 2019, 38(2): 88-96.

[6] 陳彬, 李琳, 趙志斌. 雙向全橋DC-DC變換器中大容量高頻變壓器繞組與磁心損耗計算[J]. 電工技術學報, 2017, 32(22): 123-133. Chen Bin, Li Lin, Zhao Zhibin. Calculation of high-power high-frequency transformer’s copper loss and magnetic core loss in dual-active-bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 123-133.

[7] 趙彪, 宋強, 劉文華, 等. 用于柔性直流配電的高頻鏈直流固態變壓器[J]. 中國電機工程學報, 2014, 34(25): 4295-4303. Zhao Biao, Song Qiang, Liu Wenhua, et al. High frequency-link DC solid state transformers for flexible DC distribution[J]. Proceedings of the CSEE, 2014, 34(25): 4295-4303.

[8] 王彥新, 遲青光. 方波激勵下納米晶體鐵心損耗模型建立與驗證[J]. 電機與控制應用, 2021, 48(4): 94-98. Wang Yanxin, Chi Qingguang. Establishment and verification of nanocrystal core loss model under square wave excitation[J]. Electric Machines & Control Application, 2021, 48(4): 94-98.

[9] 孫鶴, 李永建, 劉歡, 等. 非正弦激勵下納米晶鐵心損耗的計算方法與實驗驗證[J]. 電工技術學報, 2022, 37(4): 827-836. Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non-sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.

[10] Chen D Y. Comparisons of high frequency magnetic core losses under two different driving conditions - a sinusoidal voltage and a square-wave voltage[C]// 1978 IEEE Power Electronics Specialists Conference, Syracuse, NY, 2015: 237-241.

[11] 律方成, 郭云翔. 非正弦激勵下中頻變壓器鐵損計算方法對比分析[J]. 高電壓技術, 2017, 43(3): 808-813. Lü Fangcheng, Guo Yunxiang. Comparative analysis of core loss calculation methods for medium frequency transformer under non-sinusoidal excitation[J]. High Voltage Engineering, 2017, 43(3): 808-813.

[12] 張寧, 李琳, 魏曉光. 非正弦激勵下磁心損耗的計算方法及實驗驗證[J]. 電工技術學報, 2016, 31(17): 224-232. Zhang Ning, Li Lin, Wei Xiaoguang. Calculation method and experimental verification of core losses under non-sinusoidal excitation[J]. Transactions of China Electrotechnical Society, 2016, 31(17): 224-232.

[13] Sobbi B, Kaicar A, Hanen M, et al. An improved empirical formulation for magnetic core losses estimation under nonsinusoidal induction[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2146-2154.

[14] Yue Shuaichao, Li Yongjian, Yang Qingxin, et al. Comparative analysis of core loss calculation methods for magnetic materials under nonsinusoidal excita-tions[J]. IEEE Transactions on Magnetics, 2018, 54(11): 6300605.

[15] Shen Wei, Wang Fei, Boroyevich D, et al. Loss characterization and calculation of nanocrystalline cores for high-frequency magnetics applications[J]. IEEE Transactions on Power Electronics, 2008, 23(1): 475-484.

[16] Yu Xinran, Li Yongjian, Yang Qingxin, et al. Loss characteristics and model verification of soft magnetic composites under non-sinusoidal excitation[J]. IEEE Transactions on Magnetics, 2018, 55(2): 6100204.

[17] 陳彬, 李琳, 趙志斌. 典型非正弦電壓波激勵下高頻磁心損耗[J]. 電工技術學報, 2018, 33(8): 1696-1704. Chen Bin, Li Lin, Zhao Zhibin. Magnetic core losses under high-frequency typical non-sinusoidal voltage magnetization[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1696-1704.

[18] 葉建盈, 陳為, 汪晶慧. PWM波及直流偏磁勵磁下磁心損耗模型研究[J]. 中國電機工程學報, 2015, 35(10): 2601-2606. Ye Jianying, Chen Wei, Wang Jinghui. Research on the core loss model under PWM wave and DC bias excitations[J]. Proceedings of the CSEE, 2015, 35(10): 2601-2606.

Calculation and Experimental Verification of Core Loss in High Frequency Transformer under Non-Sinusoidal Excitation

Liu Huan Li Yongjian Zhang Changgeng Mu Shenghui Jin Chuhao

（State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology 300130 Tianjin China）

Soft magnetic materials are widely used in the cores of various electrical equipment, and the accurate calculation of the core loss is related to the efficiency of the equipment. Especially the accurate calculation of core loss under the condition of high frequency non-sinusoidal excitation is an important part of the optimal design of power electronic devices such as inverters, power electronic transformers and high frequency reactors.

In this paper, the calculation methods of core loss under non-sinusoidal excitation are summarized, and several improved Steinmetz empirical formulas are compared, and it is concluded that WcSE (waveform coefficient Steinmetz equation) is superior to other modified formulas in principle. The influence of magnetization process on core loss is analyzed from the principle of loss, and the conclusion that the change rate of magnetic induction intensity d/dis the key factor affecting core loss. Based on the waveform coefficient formula of WcSE the influence of d/don loss is introduced, and an improved WcSE correction formula IWcSE (improve waveform coefficient Steinmetz equation) is proposed for the calculation model of high-frequency non-sinusoidal core loss. Moreover, the loss calculation expression of the new model under high-frequency square wave and rectangular wave excitation is derived.

Then, a magnetic property test system for soft magnetic materials under high-frequency non-sinusoidal excitation was constructed, and the high-frequency magnetic characteristics experiments under square wave and rectangular wave excitation with different duty cycles were carried out on two ring nanocrystalline samples (FT-3KL and FT-3KS) in the frequency range of 10～70 kHz, and the experimental measurements of core loss under square wave and rectangular wave excitation were obtained.

Finally, the experimental values and the calculated values of several modified Steinmetz models are compared. The comparison results show that WcSE is accurate at 0.5 duty cycle, but worse at other duty cycles. But the introduction of magnetic induction intensity change rate d/dcan overcome the defect of WcSE independent of duty cycle, so IWcSE can reflect the change trend of core loss with nonlinear change of duty cycle.

The improved new model can achieve good prediction of core loss under the condition of unsaturated magnetic density in the frequency range of 10～70 kHz at square wave and rectangular wave excitation. Especially at high-frequency and low magnetic density, the calculated values of the two nanocrystalline magnetic rings are completely consistent with the experimental values. It makes up for the defect that the accuracy of core loss calculation of MSE (modified Steinmetz equation), IGSE (Improved generalized Steinmetz equation) and WcSE which are seriously reduced at frequencies exceeding 20 kHz. That verify the accuracy of IWcSE. In order to further verify the accuracy of the improved model, the error analysis of the calculated values shows that the average error of WcSE is the largest, the MSE is large, the IGSE is the second, and the IWcSE is the smallest. Moreover, the average error of IWcSE is less than 20%, which has good stability under different duty cycles and different frequencies, which verifies the universal applicability and calculation accuracy of this improved formula.

Nanocrystalline, core loss, non-sinusoidal excitation, Steinmetz experience equation

國家自然科學基金項目（52130710, 51777055, 51977122）和河北省自然科學基金創新群體項目（E2020202142）資助。

2021-10-08

10.19595/j.cnki.1000-6753.tces.211593

TM271

劉 歡 女, 1995年生, 碩士研究生, 研究方向為工程電磁場與磁技術。E-mail：1515745098@qq.com

李永建 男, 1978年生, 教授, 博士生導師, 研究方向為工程電磁場與磁技術、三維磁特性測量與建模。E-mail：liyongjian@hebut.edu.cn（通信作者）

2022-02-12

（編輯 赫蕾）