基于化歸思想的高中數學課堂教學思考

馬海燕

?新疆烏魯木齊市兵團第二中學

化歸思想是處理數學問題的重要策略，其能化復雜為簡單、化未知為已知、化非常規為常規，從而獲得解決問題的思路.在高中數學教學中，教師要靈活運用化歸思想，將問題從高維轉化成低維，促使學生更好地理解和解答問題，加深學生對問題的認識，增強學生的思維能力.

1 基于化歸思想的高中數學課堂教學策略

1.1 深挖教材內容，鞏固基礎知識

教師在培養學生化歸思想時，應從教材入手，對教材中的定義、公式、例題進行分析，讓學生明白化歸思想的來源以及如何體現.教師在備課中，應對教材中的基礎內容進行細化，讓學生在初次接觸新知識時能將新舊知識聯系起來，將思想從舊章節平穩過渡到新章節中，實現思想上的轉化.運用化歸思想要以扎實的基礎知識為前提.教師一定要讓學生先將每一個章節的知識吃透，這樣才能在不斷吸收新知識的過程中保持思路暢通.

1.2 注重思想引導，培養探究興趣

教師可以結合一些經典案例來引導學生運用化歸思想，歸納法是高中數學中常用的解題辦法，運用該方法時只需要觀察簡單的樣本就可以推導出復雜的規律，適用于解決復雜問題，教師可以在歸納法教學中讓學生接受化歸思想.例如，“摸球問題”是經典的數學問題，在紙箱中裝入2個白球、3個黑球，然后列舉出可能出現的情況.對于這一問題的解決，窮舉法顯然是缺乏代表性的，數學歸納法更加適用.在解決問題后，教師可以詢問學生：歸納法與窮舉法有什么區別？如果樣本數量不斷擴大，還能用窮舉法嗎？這樣就強化了學生對化歸思想的認識和認可.化歸思想使學生有了自主探究的可能，教師在應用化歸思想時，應引導學生打開自己的思路對問題進行轉化，靈活運用所學知識，這樣就給了學生很大的自主發揮空間，培養了學生主動探究的興趣.

1.3 把握化歸原則，避免生搬硬套

運用化歸思想應遵循以下幾個原則：一要確保化歸的規范性與有效性，應用化歸方法必須有明確的對象、設計好的目標和合適的方法，解題時必須緊盯化歸目標，盲目的化歸只會走入死胡同；二要確保邏輯上的正確性和轉化的等價性，轉化時的前因后果應是必要的、充分的，轉化后的結果應是原題的結果；三是設計合理的轉化方案，實現同一轉化目標可能需要采取多種轉化方法，簡捷合理的轉化方案是必要的，但要避免生搬硬套.

2 化歸思想的應用實踐

2.1 數形轉化

數與形的互相轉化是高中數學的重要知識，也被稱為數形結合思想.在數形轉化中，學生可以利用幾何知識來解決代數問題，或借助數量關系來研究幾何圖形的性質.幾何與代數的結合，成為高中數學中的重要一面，這也體現了化歸思想.

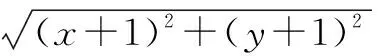
分析：這道題從表面上看是關于數的問題，但實際上卻與“形”密切相關.在求解時，可以將原問題視為求點(x,y)到點(-1,1)的距離，即求點(x,y)到直線x+y+1=0的距離.到了這一步，學生即可通過其熟悉的點到直線的距離公式求得答案.

在這一問題的處理中，巧妙地對題干進行了轉化，把代數問題轉化成了平面幾何問題，這樣做的好處就是避開求最值時要考慮條件的滿足等問題，簡化了解題過程，降低了解題難度.同時，例1的難度較低，從這樣基礎性的數形轉化思想入手，可以逐步培養學生的化歸思想，為后續學習打下良好的基礎.

2.2 正反轉化

正反轉化即當從正面入手解決問題的難度較大時，不妨從問題的反面進行考慮，通過求補集的方式逆向解決原問題.靈活運用正反轉化可以解決很多難題.正反轉化最常見的就是空間幾何問題，如物體的空間截圖、運動軌跡等，把三維空間問題轉化成二維平面問題，利用平面幾何的公式、定理、定義把待求解的問題不斷簡化，可以有效降低解題難度.

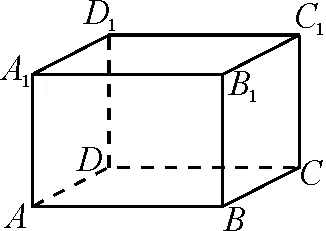
圖1

例2在長方體ABCD-A1B1C1D1中(如圖1)，已知AB=a,BC=b,AA1=c，且a>b>c.現有一物體從A點出發，沿著長方體ABCD-A1B1C1D1的表面運動到C1，求物體在運動過程中的最短路程.

分析：在這道題目中，可以將長方體ABCD-A1B1C1D1視為正六面體，將最右側平面BCC1B1與最后側平面CDD1C1展開，得到兩個俯視圖(圖2和圖3).通過平面幾何中兩點之間線段最短原理可以求出最短的路程是|AC1|，|AC1′|，|AC1″|之一.

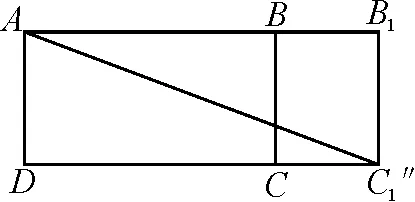
圖2

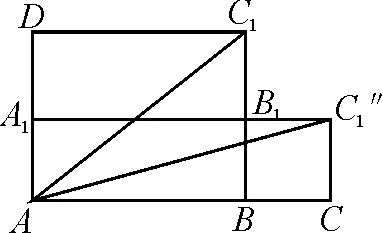
圖3

最值問題的解答，通常需要轉化成函數，但這道題目是空間幾何問題，題干也沒有給出函數式，所以轉化成函數是不可取的.平面幾何求最值的方法比較多，因此通過化歸思想可以簡化成二維平面問題，簡化解答步驟.

2.3 一般與特殊轉化

一般與特殊之間的轉化既可以是從一般途徑尋求解決特殊問題的方法，也可以是從特殊情況入手解決共性問題.

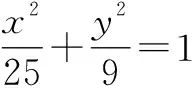
分析：在這道題目中，點B是運動的，因此很難直接得出sinA，sinC，sinB的精確值，但可以將這個一般性的問題特殊化，如將點B放到橢圓短軸的頂點，這樣就可以利用正弦定理來解答問題.

2.4 局部向整體轉化

對較復雜的數學問題，可以從總體上去把握.

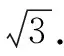
綜上，高中數學教學中有大量可以應用化歸思想解決的問題，教師在教學中應把握好轉化的切入點，引導學生將困難問題簡單化，使學生不但解決問題，更要掌握解決問題的思路.

3 結語

應用化歸思想解答數學問題可以有效降低解題難度，為學生打開新的解題思路.教師在教學中應注意鞏固學生的知識基礎，為應用化歸思想做好知識積累，并對化歸思想在不同知識點中的應用方法進行探索，改善課堂教學質量，最終提升學生的解題準確率.