高中數學解題過程中學科核心素養培養探索

湯艷麗

?江蘇省如皋中學

新時代素質教育改革提出中小學教育要以培養學生學科素養為教育教學價值導向，通過多元化學科課堂教學途徑培養學生科學的學科學習思維、正確的人生價值觀念以及高質量的自主學習能力.基于此，在高中數學教育教學過程中教師要充分利用數學學科核心素養，以培養學生綜合學科素養為教學價值導向，進而全面提升學生綜合素質.

數學學科核心素養是學生數學學習思維、方法、能力的統稱，也是歷年來高考命題考查的熱點.培養與提升學生數學學科核心素養，就是要在數學教學以及學生進行數學解題訓練過程中，注重培養與鍛煉學生快速處理數值計算與分析能力、幾何空間圖形及其位置關系想象能力、數形結合與抽象具象轉化能力以及邏輯聯想與推導能力.據此，筆者以高中數學經典例題解析為參考，探究數學解題過程與學科核心素養價值導向間的相互融合.

1 數值計算與分析能力的培養

大量的數值計算以及通過數據對某一數學現象進行深入分析是高中數學學習的一大難關.在教學過程中教師不能夠盲目夸大題海戰術帶來的數學計算能力培養的效果，否則不僅會加重學生數學學科的學習負擔，且會讓數學課堂變得枯燥，失去數學學科的教學意義.教師應該合理安排數值計算與分析題目的練習計劃，通過精準、典型的數學例題，引導學生進行數學思考，幫助學生學會從數值中發現聯系進而進行數值計算、數值建模、數值分析和后續的模型推導與總結.

例1某企業對三個工作車間的人數進行統計，其結果如表1所示.用分層抽樣的方法分別從三個車間抽取30人，其中三車間有12人.

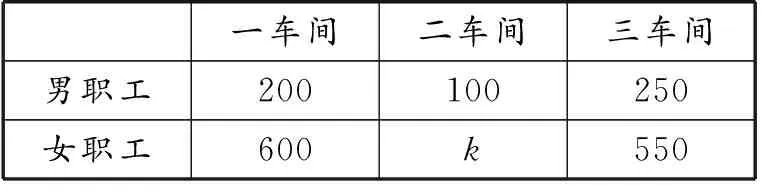
表1 三個車間人數統計 單位：人

(1)求第二車間女職工人數(k值)；

(2)為了統計企業職工請休假情況，對一車間男職工進行001—200編號，用系統抽樣的方法從中抽取5人，其全年請休假天數分別為75，79，82，73，81，且請休假73天的職員對應編號是145，問請休假75天的對應職員編號是多少？求所抽取5個職員請休假天數的方差.

分析：本題主要考查數據統計中分層抽樣、系統抽樣方法以及標準差、方差、極差的概念與計算.要求學生觀察與理解表格數據信息并準確地進行數值計算與分析，對學生數據識別與處理能力要求較高.

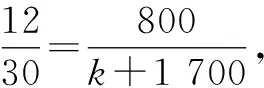
(2)由題意可知，系統抽樣過程中的抽取間距為

設請休假75天的對應職員編號是m，則由145=m+(4-1)×40，解得m=25.

所以請休假75天的對應職員編號是25.

由題設已知條件，可求得

因此，所抽取5個職員請休假天數的方差為

2 幾何空間圖形及其位置關系想象能力的培養

高中數學學習中，空間幾何圖形的性質及動態變化圖形之間位置關系是一大難點.解決此類問題需要學生具有良好的數學抽象思維、建模能力以及空間想象能力、幾何判斷能力.在教學中，教師要注重幾何基礎知識的講解以及對學生空間想象思維的培養，通過解題訓練鍛煉學生想象能力，幫助學生學會從已知數學條件中發現問題并以扎實的數學基礎探索解決問題的有效方法.

例2如圖1，在四棱錐P-ABCD中，底面ABCD是邊長為4的正方形，且AC與BD相交于點O，點E是線段BP的中點，滿足AP=CP，BP=DP.

(1)證明：AB⊥OP；

(2)設OP=2，求三棱錐A-BCE的體積.

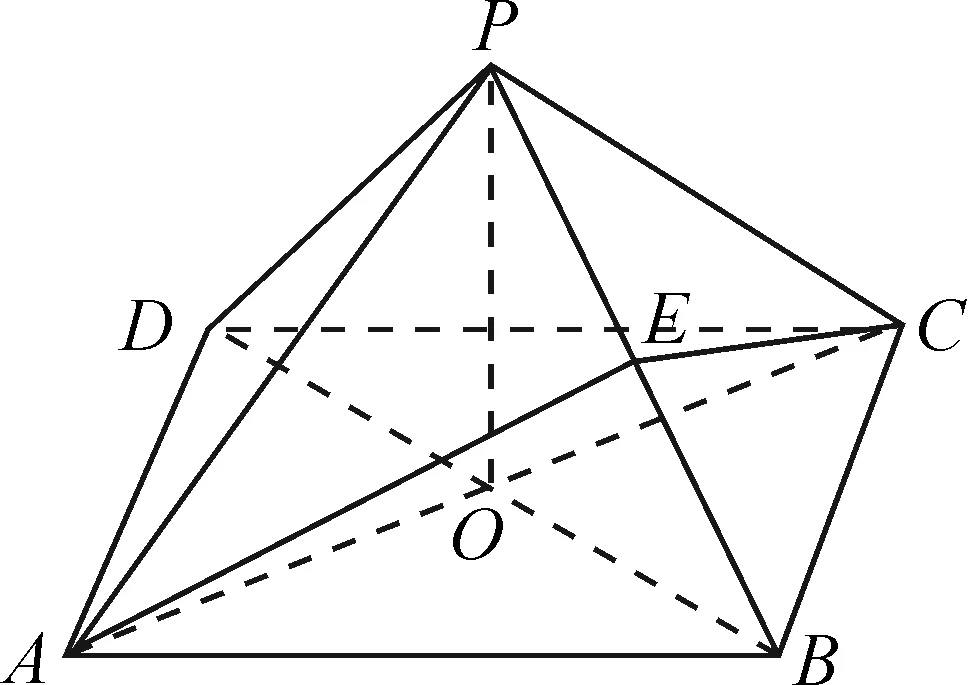
圖1

分析：本題主要考查空間圖形的判斷及相應體積求解公式、空間中兩直線的位置關系.要求學生具有一定的空間想象能力、邏輯推導能力并熟練掌握常見幾何體的面積、體積公式.

解析：(1)因為棱椎的底面ABCD是正方形，且點O是AC與BD的交點，所以點O為AC，BD的中點.

又因為AP=CP，BP=DP，所以AC⊥OP，BD⊥OP.

因為AC∩BD=O，AC，BD均在平面ABCD內，所以OP⊥平面ABCD.

故AB⊥OP.

(2)由題設條件，易知

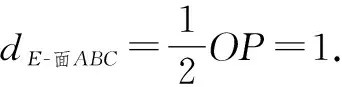
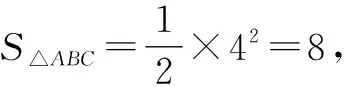
3 數形結合與抽象具象轉化能力的培養

“幾何直觀”是新課程素質教育教學大綱所提出的高中數學關于培養學生數學思維的核心概念之一.因此，在教學中高中數學教師要注重對學生數形結合思維的培養.在相關題目解答過程中，教師要引導學生學會通過對事物的直接感知，發現數學問題背后事物的本質聯系，依據想象構建清晰的數學圖形并建立明確的數形聯系，利用數形轉換解決數學問題.

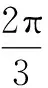
(1)求母線l的長度；

(2)求此圓錐的體積.

分析：此題主要考查幾何圖形間的位置關系、圓錐側面展開圖及其面積公式、圓錐體積公式等.要求學生將題中抽象的數學語言轉換為直觀的數學圖形，從數形結合的角度找到解題關鍵點.

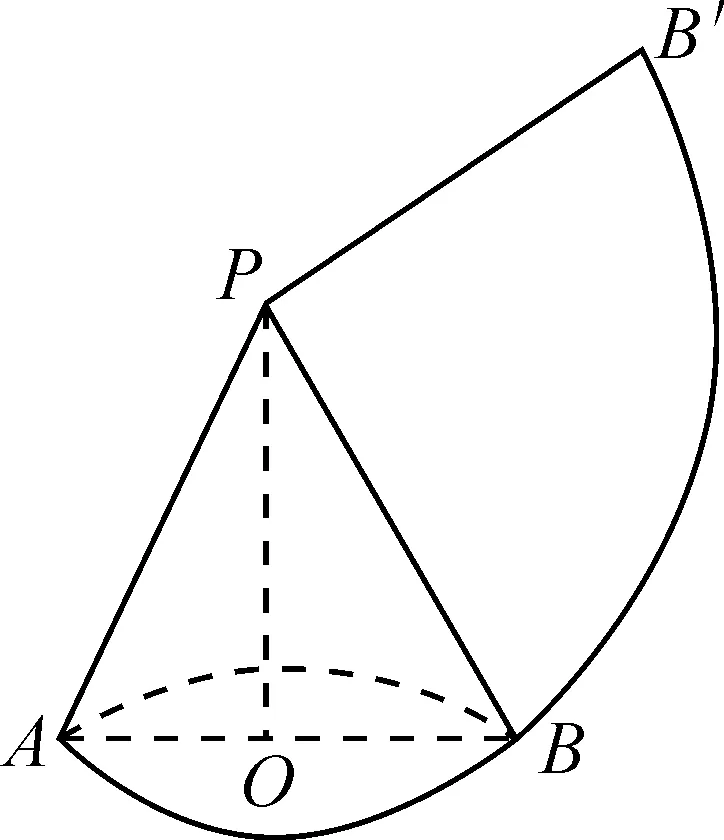
圖2

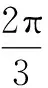
由2πr=2π，得r=1.所以圓錐的體積為

4 邏輯聯想與推導能力的培養

邏輯聯想與推導能力要求學生從現有的數學理論認知和相關數學命題出發，從一個問題切入點聯想豐富的數學理論知識，以全面的數學視角分析問題并推斷涵蓋面更為廣泛的數學命題.在高中數學解題中考查學生邏輯聯想與推導能力主要體現在尋找數學規律上，如數列中的楊輝三角等數學問題.教師要充分理解此類數學問題的本質規律，在解題過程中訓練學生邏輯思維.

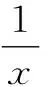
(1)判斷集合B={-1,0,1}是否為“閉集”，并說明理由；

(2)假設集合A是閉集，證明：若x，y∈A，則有x+y∈A；

(3)假設集合A是一個“閉集”，判斷命題“若x∈A，則有x2∈A”的真假，并說明理由.

分析：此類題目是高中數學關于集合的概念與性質內容考查常見的出題方式，在學生已有的關于集合理論知識的基礎上提出一個新的定義，要求學生在對集合概念與性質理解的基礎上，利用邏輯推理對另外的數學命題加以判斷，以找到命題之間的本質聯系，理解其中的數學含義.

解析：(1)因為-1-1=-2?B,所以由“閉集”定義可判斷集合B={-1,0,1}不是閉集.

(2)證明：因為集合A是閉集，所以0∈A.若y∈A,則0-y=-y∈A.

所以由x∈A,可知x-(-y)=x+y∈A.

(3)因為x，y∈A，1∈A，所以x-1∈A.于是，當x≠0，且x≠1時，有

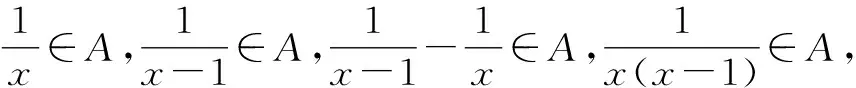
由(2)可知，x(x-1)+x∈A，即x2∈A.

故命題“若x∈A，則有x2∈A”是真命題.

通過數學經典例題的講解以及學生對相關數學問題的解答與思考，能夠幫助學生建立系統的數學思維模式，鍛煉其發現并解答數學問題的能力.但教師要走出題海戰術誤區，從關注學生解題結果轉向關注學生解題過程.教師要引導學生在解題過程中提高自身數值計算與分析能力、幾何空間圖形及其位置關系想象能力、數形結合與抽象具象轉化能力以及邏輯聯想與推導能力等，充分將數學學科核心素養與高中數學課堂教學過程相融合.教導學生解題時不能急于求成，而應反復斟酌與推敲，學會以不變應萬變，幫助學生形成良好的數學解題習慣與思維模式，進而全面提升學生綜合素質.這將對學生今后的學科學習大有裨益.