經歷數形結合過程 感悟數形互助內涵
——《數與形》教學
文|戚彩紅 田小紅
【教學內容】
人教版六年級上冊第八單元第一課時。
【課前思考】
《數與形》一課的教學,例題和練習中每道題的規律都不一樣,很容易上成找規律的課。小學數學中“數形結合”思想散落于各個年級之中。如:數量關系通過“數”來描述數與數之間的關系,畫圖分析數量關系就是“形”的表現形式;長度、面積、體積是通過“形”來展現其直觀形式的,而計算公式又是通過“數”來呈現的;在“統計與概率”中,“數”與“形”更加清晰。受小學生的年齡特征和認知特點所限,思想方法常隱含在眾多的數學知識之中。《數與形》一課就是把這層窗戶紙捅破,讓學生體驗“數形結合”的數學思想和方法。《義務教育數學課程標準(2022年版)》中指出,學生幾何直觀素養的具體表現之一在于能夠建立形與數的聯系,構建數學問題的直觀模型,探索解決問題的思路。所以本課不應停留在讓學生會用總結得出的規律解決問題,更重要的是讓學生在學習過程中感悟數形結合的思想方法,能用數學的思維解決問題。
為了解不同教材采用的不同圖形中哪種更能引發學生思考,筆者進行了前測(見文末二維碼)。根據前測結果,我們改變教學素材,采用圓點圖,充分發揮學生的自主探究能力。
【教學過程】
一、初步體驗數形結合——數中有形,形中有數
動態依次出示下圖

師:你看到了什么形狀?
生:圓點搭成了三角形。
師:你能計算出這里第六個圖形一共有多少小圓片嗎?說說你是怎么計算的。
生1:1+2+3+4+5+6=21。
生2:1+2+3+4+5+6=(1+6)×6÷2=21。
生3:1+2+3+4+5+6=(1+6)×3=21。
課件演示生2 和生3 的算理:
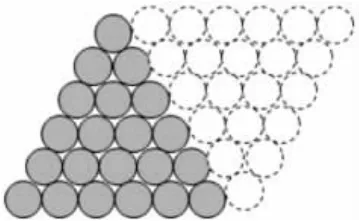
小結:從1 開始的連續自然數相加的和=(1+末項)×項數÷2,并且末項=項數。
師:像1、3、6、10、15……用圓點表示這些數,我們發現這些圓點都可以擺成等邊三角形。2500多年前的古希臘,數學家畢達哥拉斯,就發現了這些數的特點,他稱這樣的數為“三角形數”。你還能繼續往下找三角形數嗎?你是怎么找到的?
生:三角形數就是從1 開始的連續自然數相加的和。
師:回顧剛才的學習,我們先看到了圖形,接著用算式表示了圓點的總數,然后又用圖形幫助我們找到了簡便計算的方法。有數,也有形;數中有形、形中有數,這節課我們來學習《數與形》。
二、經歷過程,感受數形互助——依數思形,依形思數
1.認識正方形數,感受“以形助數”
教師出示課件,動態演示三角形數,隱去偶數層:
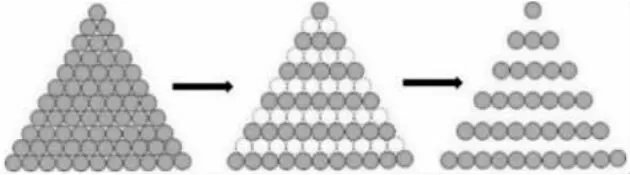
師:你能算出現在這個圖形中小圓片的個數嗎?說說你是怎么算的。
生:1+3+5+7+9+11=36。
師:能不能像剛才那樣用圖形來說明計算的過程?請你擺一擺小圓片,看看有什么發現。
師:生2 的方法中你能找到1+3+5+7+9+11 這個算式嗎?試著找找看。
師:觀察這個圖形,有什么發現?
生:擺成了邊長是6 的正方形,1+3+5+7+9+11=6×6=36。
生:1+3+5+7+9=5×5=25,擺成了邊長是5 的正方形,剛好是5個連續奇數。
師:所以,像1、4、9、16、25、36……這樣的數,叫作正方形數。正方形數可以怎樣得到呢?
生:正方形數是從1 開始的連續奇數相加的和。
小結:從1 開始的連續奇數相加的和=奇數個數的平方。
2.嘗試練習,加深理解
師:想一想,怎樣才能算得又對又快?
1+3+5+7+9+11+13+15=__________________=92
1+3+5+7+5+3+1=__________
1+3+5+7+9+11+13+11+9+7+5+3+1=______________
生:想到這個式子的圖形,計算就快了。
課件演示:

小結:圖形幫助我們解決了計算的問題。
3.探究方陣圖,感受“以數解形”
師:(出示6×6 的方陣圖)你能用哪些算式來計算這里一共有多少個圓點?想到幾種就寫幾種。
(學生獨立操作,交流反饋作品)
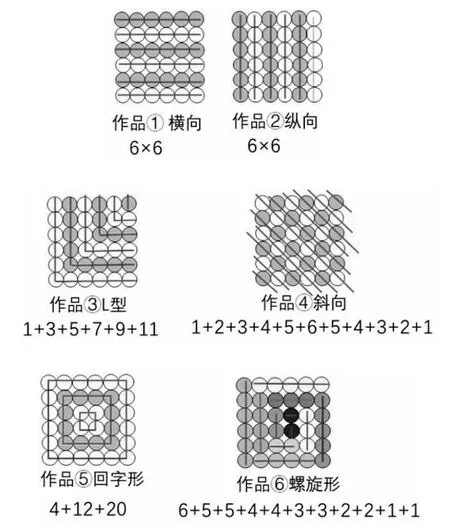
師:同學們,回顧一下剛才我們的探究過程。在探究正方形數時,我們從一個算式想到相對應的形,形幫助我們解決了數的計算問題;在探究6×6 方陣圖時,用算式來解決這個形的問題,我們發現可以有很多不同的算法,最終結果都是36 個。現在你們覺得數和形之間有著怎樣的關系呢?
生:數和形關系密切,你中有我,我中有你,互相幫助。
小結:看到數,我們可以想象它對應的形;看到形,我們可以想它對應的數。數形結合,可以幫助我們解決問題。
三、深刻感悟數形內涵——數形緊密聯系、不可分割
1.探究長方形數,解決問題
師:研究了三角形數、正方形數,讓我們猜想一下,有沒有長方形數?五邊形數、六邊形數……這樣的數呢?來看看剛才的作品,有沒有給你啟發的地方?
學生思考后,教師課件演示:
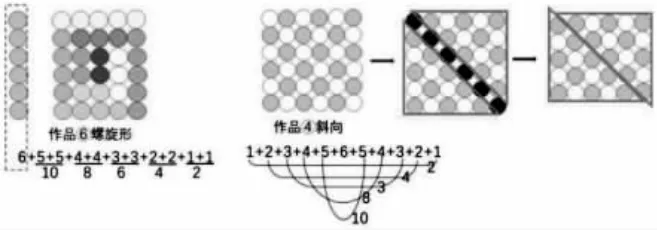
生:作品⑥和作品④去掉6,都可以轉化成2+4+6+8+10 這樣的從2 開始的連續偶數相加。
生:我發現圓點組成了長和寬分別是5 和6 的長方形。
師:你能在長方形圓點圖中找到2+4+6+8+10 這個算式嗎?
生:這樣圖畫得更加清晰一些。
小結:(1)從2 開始的連續偶數相加的和是長方形數。(2)從2開始的連續偶數相加的和=偶數的個數×(偶數的個數+1)。
2.梳理關系,深化理解
師:三角形數、正方形數、長方形數之間有沒有關系?如果有,是怎樣的關系?要尋找它們之間的關系,我們把它們都擺在一起來找找看。
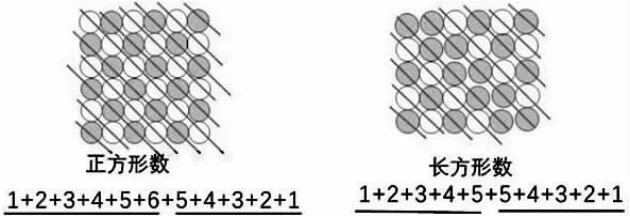
生1:兩個相鄰的三角形數可以組成一個正方形數。
生2:兩個完全一樣的三角形數可以組成一個長方形數。
根據學生的回答,出示課件:

師:畢達哥拉斯學派堅信“萬物皆數”,他們還找到了最完美的數、完全數、親和數、勾股數等。有三角形數、正方形數、長方形數,還有五邊形數、六邊形數等等,同學們可以在課后繼續研究。

