矩陣方程AX=B的譜范數(shù)約束解

劉喜富, 羅 樂

(重慶師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 重慶 401331)

1 引言與預(yù)備知識

EA=Im-AA+,FA=In-A+A.

對于任意的ξ>0,Sveξ(A)表示的是A的奇異值中大于或等于ξ的個(gè)數(shù).對于任意矩陣W,W是壓縮矩陣當(dāng)且僅當(dāng)‖W‖2≤1,W是Hermitian壓縮矩陣當(dāng)且僅當(dāng)‖W‖2≤1并且W=W*.

約束矩陣方程的求解在矩陣?yán)碚摵推渌芏囝I(lǐng)域中都起著重要的作用.近些年,約束線性矩陣方程AX=B的求解問題一直是研究的熱門問題之一,這些約束主要包括：Hermitian、(半)正定、(反)自反、中心對稱、范數(shù)等.矩陣方程AX=B約束解的結(jié)論在振動(dòng)理論及其逆問題、結(jié)構(gòu)化設(shè)計(jì)、統(tǒng)計(jì)和控制理論等領(lǐng)域有著廣泛的應(yīng)用,近年來諸多學(xué)者都對其有了很深的研究：文獻(xiàn)[1-2]利用矩陣的廣義逆給出了線性矩陣方程AX=B存在一般解的充要條件及解的表達(dá)式;Li等[3]給出了矩陣方程AX=B的解在特殊情況下關(guān)于秩的結(jié)論;Liu等[4]研究了矩陣方程AX=B的Hermitian解和半正定解在保范擴(kuò)張下的應(yīng)用;王婧等[5]研究了矩陣方程AX=B的(反)自反問題以及最佳逼近問題;Zhang等[6]利用矩陣的分解研究了矩陣方程的P、Q的(反)自反解問題;Sou等[7]給出了問題

‖A-BXC‖2<1

最小秩解的一般形式.

當(dāng)矩陣方程

AX=B

(1)

分別存在一般解、Hermitian解、半正定解時(shí),本文主要考慮該矩陣方程在2種譜范數(shù)約束下的解,即最小譜范數(shù)解，以及譜范數(shù)小于1的解.

問題 1給定矩陣A∈Cm×l,B∈Cm×k,求相容矩陣方程AX=B在以上2種約束條件下的一般解.

問題 2給定矩陣A∈Cm×l,B∈Cm×l,求相容矩陣方程AX=B在以上2種約束條件下的Hermitian解.

問題 3給定矩陣A∈Cm×l,B∈Cm×l,求相容矩陣方程AX=B在以上2種約束條件下的半正定解.

為了得到以上問題的解,引入以下引理.

引理 1.1[5]1) 給定矩陣A∈Cm×l,B∈Cm×k,矩陣方程AX=B相容的充要條件為AA+B=B.有解時(shí),該方程的一般解可以表示為X=A+B+FAY,其中Y是適當(dāng)階數(shù)的任意矩陣.

2) 給定矩陣A∈Cm×l,B∈Cm×l,相容矩陣方程AX=B存在Hermitian解的充要條件為BA*是Hermitian矩陣.有Hermitian解時(shí),該方程的Hermitian解可以表示為

X=A+B+FA(A+B)*+FAYFA,

其中Y是適當(dāng)階數(shù)的任意Hermitian矩陣.

3) 給定矩陣A∈Cm×l，B∈Cm×l,相容矩陣方程AX=B存在半正定解的充要條件為BA*是半正定矩陣,且r(BA*)=r(B).有半正定解時(shí),該方程的半正定解可以表示為

X=B*(BA*)+B+FAYFA,

其中Y是適當(dāng)階數(shù)的任意半正定矩陣.

其中

是適當(dāng)階數(shù)的任意Hermitian壓縮矩陣.

設(shè)矩陣A∈Cm×n的奇異值分解為

V*、U、V都是酉矩陣,其中

Λ1=diag(σ1,σ2,…,σk),
Λ2=diag(σk+1,σk+2,…σl),
σ1≥σ2≥…≥σk≥1>σk+1≥…≥σl>0,r(A)=l,

則可定義

引理 1.4[4]給定矩陣A∈Cm×n,B∈Cm×mx,C∈Cnx×n,其中B是列滿秩矩陣,C是行滿秩矩陣,B、C的奇異值分解為

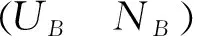
X=

其中

并且

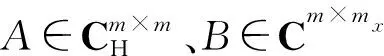
‖A-BXB*‖2<1.

引理 1.5[9]給定矩陣A∈Cm×m,B∈Cm×n,C∈Cn×n,D∈Cn×m,設(shè)A、C是可逆矩陣,則A+BCD可逆的充要條件為C-1+DA-1B可逆,此時(shí)它的逆可表示為

(A+BCD)-1=

A-1-A-1B(C-1+DA-1B)-1DA-1.

引理 1.6[10]給定矩陣

其中A、D是Hermitian矩陣,則M>0的充要條件為A>0,D-B*A+B>0.

2 問題1的解

給定矩陣A∈Cm×l,B∈Cm×k,A的奇異值分解為

(2)

其中U、V都是酉矩陣,Σ=diag(σ1,σ2,…,σr),
σ1≥σ2≥…≥σr>0, r(A)=r.

(3)

其中X2為適當(dāng)階數(shù)的任意矩陣.

定理 2.1給定A∈Cm×l,B∈Cm×k,相容矩陣方程(1)的解如(3)式所示,該方程的最小譜范數(shù)解可表示為

A+B+FAY,

(4)

K為適當(dāng)階數(shù)的任意壓縮矩陣.

證明由引理1.2可得(4)式成立,即

μ=min‖X‖2=‖Σ-1B1‖2=‖A+B‖2.

定理 2.2給定A∈Cm×l,B∈Cm×k,相容矩陣方程(1)的解如(3)式所示,該方程存在譜范數(shù)小于1的解的充要條件為‖A+B‖2<1.該方程有約束解時(shí),它的一個(gè)約束解為

(5)

證明AX=B的解如(3)式所示,它的譜范數(shù)可轉(zhuǎn)化為

其中

‖A+B‖2<1.

方程(1)有約束解時(shí),則

故方程(1)的一個(gè)譜范數(shù)小于1的解為(5)式.

給定矩陣

A=

B=

例 2.1矩陣方程(1)解的最小譜范數(shù)為μ=0.795,此時(shí)它的最小譜范數(shù)解如(4)式所示：

X=A+B+FAY,

其中

例 2.1矩陣方程(1)的譜范數(shù)小于1的一個(gè)解如(5)式所示,即可表示為

3 問題2的解

給定矩陣A∈Cm×l,B∈Cm×l,A的奇異值分解如(2)式所示.由引理1.1可得,矩陣方程(1)存在Hermitian解時(shí),B可以相應(yīng)的表示為

且該方程的Hermitian解可以表示為

(6)

其中X22是適當(dāng)階數(shù)的任意的Hermitian矩陣.

定理 3.1給定矩陣A∈Cm×l,B∈Cm×l,矩陣方程(1)的Hermitian解如(6)式所示,該方程的Hermitian最小譜范數(shù)解可表示為

A+B+FA(A+B)*+FAYFA,

(7)

其中

W是適當(dāng)階數(shù)的任意Hermitian壓縮矩陣.

證明由引理1.3易證(7)式成立,即

定理 3.2給定矩陣A∈Cm×l,B∈Cm×l,矩陣方程(1)的Hermitian解如(6)式所示,方程存在譜范數(shù)小于1的Hermitian解的充要條件為‖A+B‖2<1,該方程有Hermitian約束解時(shí),它的一個(gè)約束解可以表達(dá)為

A+B+FA(A+B)*+FAYFA，

(8)

其中Y如定理3.1所示,則

(9)

證明AX=B的Hermitian解如(6)式所示,它的譜范數(shù)可轉(zhuǎn)化為

其中

,

方程(1)有約束解時(shí),由引理1.4和引理1.5可得：

再次應(yīng)用引理1.4可得(9)式及矩陣方程(1)的一個(gè)譜范數(shù)小于1的Hermitian解為(8)式.

給定矩陣

A=

B=

例 3.1矩陣方程(1)解的最小譜范數(shù)為μ=0.717,此時(shí)它的最小譜范數(shù)解如(7)式所示,即

X=A+B+FA(A+B)*+FAYFA,

其中FA、V*如例2.1所示.

例 3.2矩陣方程(1)的譜范數(shù)小于1的解如(8)式所示,即

X=A+B+FA(A+B)*+FAYFA,

其中FA如例2.1所示,A+B+FA(A+B)*如例3.1所示，即

即

4 問題3的解

給定矩陣A∈Cm×l,B∈Cm×l,A的奇異值分解如(2)式所示.由引理1.1可得,矩陣方程(1)存在半正定解時(shí),B可以相應(yīng)的表示為

且方程(1)的半正定解可表示為

X=

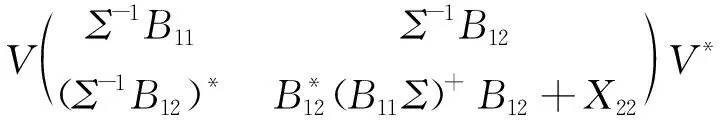
(10)

其中X22是適當(dāng)階數(shù)的任意半正定矩陣.

定理 4.1給定矩陣A∈Cm×l,B∈Cm×l,矩陣方程(1)的半正定解如(10)式所示,該方程的一個(gè)最小譜范數(shù)半正定解可表示為

B*(BA*)+B.

(11)

證明AX=B的半正定解如(10)式所示.由于

X22是任意的半正定矩陣,故可得

由偏序的性質(zhì)可得

‖X‖2=

取X22=0時(shí)上式等式成立.此時(shí),矩陣方程(1)的一個(gè)半正定最小譜范數(shù)解為(11)式.

值得注意的是,定理4.1的證明并未使用保范擴(kuò)張定理,這是因?yàn)樵?10)式中不能保證存在半正定矩陣X22使得

當(dāng)?shù)仁匠闪r(shí),可通過保范擴(kuò)張定理結(jié)合半正定矩陣的性質(zhì)得到通解.

定理 4.2給定矩陣

A∈Cm×l,B∈Cm×l,

矩陣方程(1)的半正定解如(10)式所示,該方程存在譜范數(shù)小于1的半正定解的充要條件為

‖B*(BA*)+B‖2<1.

該方程有譜范數(shù)小于1的半正定解時(shí),它的解可表示為

X=

B*(BA*)+B+FAYFA,

(12)

其中Y如定理3.1所示,即

證明AX=B的半正定解如(10)式所示.由定理4.1可得

min‖X‖2≥

‖B*(BA*)+B‖2,

即方程(1)存在譜范數(shù)小于1的半正定解的充要條件為‖B*(BA*)+B‖2<1.有解時(shí),由偏序的性質(zhì)可得

顯然I-Σ-1B11>0,則由引理1.6可得

(Σ-1B12)*(I-Σ-1B11)+Σ-1B12>0,

即

值得注意的是,不同于定理2.2和定理3.2,定理4.2沒有利用引理1.4進(jìn)行求解問題.

實(shí)際上引理1.4可適用于該問題的求解,但由于得出結(jié)果為X22=0,結(jié)果顯然,且證明過程冗雜,故引理1.4利用偏序予以證明.

給定矩陣

A=

B=

例 4.1矩陣方程(1)解的最小譜范數(shù)為μ=0.895,此時(shí)它的最小譜范數(shù)解如(10)式所示,即

例 4.2矩陣方程(1)的譜范數(shù)小于1的解為

X=B*(BA*)+B+FAYFA,

其中FA、V*如例2.1所示,B*(BA*)+B如例4.1所示,即

5 結(jié)束語

對于譜范數(shù)約束條件‖X‖2<1,在實(shí)際應(yīng)用中,常遇到約束條件：對于任意的ξ(ξ>0),則

‖X‖2<ξ.

實(shí)際上,本文的結(jié)論也同樣適用于該約束：對于矩陣方程AX=B,令

則AX=B可轉(zhuǎn)化為AξXξ=B,則