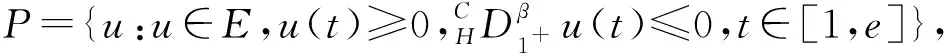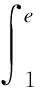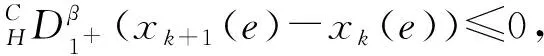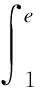一類具有p-Laplacian算子的Caputo-Hadamard型分數階微分方程解的存在性
南軍平, 胡衛敏, 蘇有慧, 楚 陽
(1. 伊犁師范大學 數學與統計學院, 新疆 伊寧 835000; 2. 徐州工程學院 數學與統計學院, 江蘇 徐州 221116; 3. 伊犁師范大學 應用數學研究所, 新疆 伊寧 835000; 4. 蘇州大學 數學科學院, 江蘇 蘇州 215006)
分數階微分方程在生物等眾多領域得到了廣泛的應用,使得分數階微分方程理論得到了快速的發展,出現了大量關于它的專著和文獻,詳見文獻[1-5].現在分數階微分方程理論中,大部分是關于Riemann-Liouville型和Caputo型[6-8]分數階微積分的,對Caputo-Hadamard型[9-13]分數階導數的研究較少.因此,研究Caputo-Hadamard分數階微分方程具有積極的意義.
Hadamard分數階導數是1892年由Hadamard提出的,其意義在于積分的核包含一個任意指數的對數函數.在文獻[9]中,利用上下解方法證明了如下非線性Captuo-Hadamard分數階微分方程解的存在性

文獻[11]通過上下解方法和不動點定理證明了如下分數階邊值問題解的存在唯一性
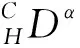
文獻[9]研究了非線性Captuo-Hadamard分數階微分方程,但該方程不帶有p-Laplacian算子;文獻[11]研究了分數階微分方程非線性部分不含分數階導數以及邊值條件為整數階導數,沒有研究非線性部分含分數階導數和邊值條件為分數階導數的情形.受文獻[9,11,14-15]啟發,本文研究如下一類非線性項包含分數階導數的具有p-Laplacian算子的分數階微分邊值問題解的存在性
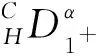
1 相關定義及引理
下面給出一些定義及相關引理.
定義 1[1]令α>0,則函數y:[1,+∞)→R的α階Hadamard分數階積分定義為
其中,Γ(·)表示Gamma函數,n-1<α R:δn-1y(t)∈AC[a,T]}. 定義 2[10]1) 如果α≠n,則α>0階Caputo-Hadamard分數階導數定義為 HIn-αδny(t). 2) 如果α=n,則n階Caputo-Hadamard分數階導數定義為 其中,ci∈R,i=0,1,2,…,n-1. 引理 2若h(t)∈C([1,e],R),c,d∈R,則邊值問題 (4) 有唯一解 u(t)=c- (6) 其中 (7) (8) 證明令 邊值問題(4)可以分解為以下邊值問題: (9) 和 (10) 邊值問題(9)由引理1可得 由m′(1)=0可得c1=0.由m(e)=φp(d)有 φp(d), 從而 即 (11) 同理,邊值問題(10)可得 由 從而 由Gm(t,s)、Gu(t,s)這2個式子的定義易得下述引理. 引理 3對任意(t,s)∈[1,e]×[1,e],有 Gm(t,s)≥0,Gu(t,s)≥0, 且Gm(t,s)、Gu(t,s)在[1,e]×[1,e]上連續. 記 取范數 ‖u‖=‖u‖1+‖u‖2, 其中 則(E,‖·‖)是Banach空間. 定義 3若u∈AC1[1,e],滿足 則稱u=u(t)為邊值問題(3)的下解. 定義 4若u∈AC1[1,e],滿足下述式子 則稱u=u(t)為邊值問題(3)的上解. 引理 4假設條件: (S1) 若K∈C([1,e]×R×R),對任意t∈[1,e]且0≤n1≤n2,z2≤z1≤0∈R,都有 0≤-K(t,n1,z1)≤-K(t,n2,z2); (S2) 設g∈([1,e]×R),對任意t∈[1,e]且w1≤w2∈R時,有 0≤g1(t,w1)≤g1(t,w2). 若條件(S1)和(S2)均成立,且邊值問題(3)存在非負下解xk∈P,k∈{0,1,2,…},則邊值問題 存在唯一解 xk+1=xk+1(t)∈P, 且為問題(3)的下解,并滿足xk?xk+1. 證明由引理2,對任意xk∈P,可知邊值問題(14)存在唯一解 xk+1=xk+1(t)∈P, 即 從而有xk+1(t)∈P. 下面證明xk(t)?xk+1(t)且xk+1=xk+1(t)是邊值問題(3)的下解.由于xk=xk(t)是邊值問題(3)的下解,則有 通過(14)和(15)式有 記 則有 則有 可得以下邊值條件 通過引理4和(11)式,可得 利用φp的單調性,有 從而可得以下邊值條件 因此 xk+1(t)-xk(t)= 即可得xk(t)?xk+1(t).由條件(S1)和(S2)可得 即xk+1=xk+1(t)是邊值問題(3)的下解. 類似引理4的證明可得下面引理. 引理 5若引理4的條件(S1)和(S2)均成立,邊值問題(3)存在上解yk∈P,則邊值問題 存在唯一解yk+1=yk+1(t)∈P,且為問題(3)的上解,滿足yk+1?yk. 定理 1若引理4的條件(S1)和(S2)成立,邊值問題(3)存在上解y0和下解x0,且x0?y0,其中x0,y0∈P,則邊值問題(3)存在解x*和y*,x*,y*∈P,且滿足x0?x*?y*?y0. 證明設x0和y0∈P為初始元,由引理4和引理5得到序列{xk}和{yk},并且xk與yk(k=0,1,2,3,…)分別為邊值問題(3)的下解和上解.由xk?xk+1可知{xk}單調遞增;由yk+1?yk可知{yk}單調遞減. 下面用數學歸納法證明 xn?yn,n=0,1,2,3,…. 當n=0時,x0?y0成立;當n=k時,假設xk?yk成立,即 由引理4的條件(S1)和(S2)有 通過(14)和(17)式有 可得 xk+1?yk+1, 即 x0?x1?…?xk?…? yk?…?y1?y0, 所以序列{xk}和{yk}一致有界.又由于Gm、Gu和K在[1,e]×[1,e]上連續,且由φp的定義可知φp和φq是連續的,從而序列{xk}和{yk}等度連續.利用Arzela-Ascoli定理可知序列{xk}和{yk}是相對緊的,則存在x*和y*使 下面證明x*和y*為邊值問題(3)的解.由Gm、Gu、K和φp的連續性,利用Lebesgue控制收斂定理可得 即 x*=x*(t) 為邊值問題(3)的解. 同理 y*=y*(t) 也是邊值問題(3)的解,且有 致謝徐州工程學院科研項目(XKY2020102)對本文給予了資助,謹致謝意.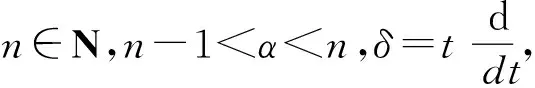
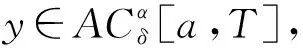

2 解的存在性