廣義色散方程的李群分析、最優(yōu)系統(tǒng)、對稱約化及精確解

胡彥鑫, 郭增鑫, 辛祥鵬

(聊城大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 山東 聊城 252000)

在非線性波以及孤立子理論的相關(guān)物理問題中,色散方程占據(jù)著相當(dāng)重要的位置,它是解決波傳播問題的方程.根據(jù)色散方程能夠得到宏觀上波傳播的速度,例如波峰移動的速度.色散方程在流體力學(xué)研究中起著重要的作用,在面對許多復(fù)雜的物理問題時,人們通常會將其轉(zhuǎn)化為偏微分方程的求解問題[1].因此,對于如何構(gòu)造偏微分方程的精確解逐漸成為物理和數(shù)學(xué)等學(xué)科諸多學(xué)者研究的重要問題.隨著時間的推移,求解偏微分方程的方法也越來越多,例如，經(jīng)典李群方法[2]、F-展開法[3]、橢圓函數(shù)展開法[4]、試探函數(shù)法[5]和雙曲函數(shù)展開法[6]等.

考慮如下形式的五階色散方程

ut+αuxuxx+βuxxxxx+γux=0,

(1)

其中,u=u(x,t),α、β、γ為任意常數(shù).方程(1)已有許多研究者采用不同的方法進行了深入探討,如:2009年宋國亮等[7]采用試探函數(shù)法求出方程(1)在γ=0時的孤波解和有理解等；文獻(xiàn)[8-9]采用(G′/G)展開法構(gòu)造了方程(1)特殊形式的多個行波解,并且討論了ux在不同次冪下的該色散方程解的情況,最終得出該方程的行波解.本文在已有研究的基礎(chǔ)上對方程增加一項色散控制項,使得方程在不失去物理意義的前提下能夠模擬更多的傳播現(xiàn)象.同時，從李群方法入手,結(jié)合多種輔助函數(shù)展開法構(gòu)造了方程(1)的孤子解和三角函數(shù)解等.

1 方程(1)的對稱

設(shè)方程(1)的向量場為

(2)

其中ξ(x,t,u)、τ(x,t,u)、φ(x,t,u)是未知函數(shù).若向量場(2)為方程(1)的李點對稱,就要滿足

pr(5)V(Δ)|Δ=0=0,

(3)

其中

Δ=ut+αuxuxx+βuxxxxx+γux,

可以得到方程(1)的五階延拓為

pr(5)V=φt+φx(αφxx+γ)+βφxxxxx=0,

(4)

(4)式中的φt、φx、φxx、φxxxxx是由(2)式中的ξ(x,t,u)、τ(x,t,u)、φ(x,t,u)的微分項決定:

φt=Dt(φ-ξux-τut)+ξuxt+τutt,

(5)

φx=Dx(φ-ξux-τut)+ξuxx+τuxt,

(6)

φxx=Dxx(φ-ξux-τut)+ξuxxx+τuxxt,

(7)

φxxxxx=Dxxxxx(φ-ξux-τut)+

ξuxxxxxx+τuxxxxxt,

(8)

這里(5)～(8)式中的Dx、Dt是關(guān)于t、x的全微分算子.

將(5)～(8)式代入(4)式,由對稱的相關(guān)條件,令包含u的各階導(dǎo)數(shù)的系數(shù)均等于零,可得到關(guān)于ξ、τ、φ的決定方程組,求解后可得方程(1)的李點對稱

(9)

其中，C1、C2、C3、C4為任意常數(shù).

接下來對上述對稱進行分類討論:

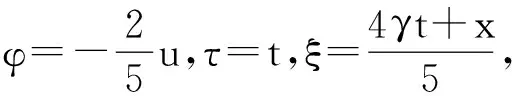
(10)

2) 當(dāng)C2=1,C1=C3=C4=0時,φ=0,τ=1,ξ=0,代入(2)式,得到

(11)

3) 當(dāng)C3=1,C1=C2=C4=0時,φ=1,τ=0,ξ=0,代入(2)式,得到

(12)

4) 當(dāng)C4=1,C1=C2=C3=0時,φ=0,τ=0,ξ=1,代入(2)式,得到

(13)

綜上,得到了方程(1)的4個李點對稱.

下面將利用這4個基本對稱構(gòu)造出方程(1)的一維最優(yōu)系統(tǒng),并利用對稱將方程(1)轉(zhuǎn)化為常微分方程.

2 李代數(shù)與最優(yōu)系統(tǒng)

前面已求出的4個方程(1)的李點對稱向量場為

(14)

接下來進行最優(yōu)系統(tǒng)的計算.首先由李括號[10]運算定義

[Vi,Vj]=ViVj-VjVi,

得到李代數(shù)交換子表(如表1所示).

表 1 李代數(shù)交換子表

再由李代數(shù)伴隨[11]表達(dá)式

得到李代數(shù)伴隨作用表(如表2所示).

表 2 李代數(shù)伴隨表

接下來進行最優(yōu)系統(tǒng)的構(gòu)造.首先假設(shè)由向量場Vi(i=1,2,3,4)構(gòu)成如下的李代數(shù)L4:

V=a1V1+a2V2+a3V3+a4V4,

其中a1、a2、a3、a4是任意常數(shù).構(gòu)造最優(yōu)系統(tǒng)的目的是利用伴隨作用盡可能多的消掉ai(i=1,2,3,4),使得V的表達(dá)式盡可能簡單.

a1V1+a2V2+a3V3+a4V4-ε[a1[V2,V1]+

a2[V2,V2]+a3[V2,V3]]+a4[V2,V4]]-…=

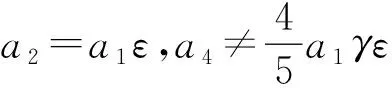
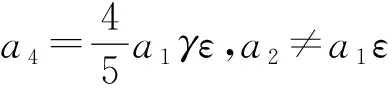
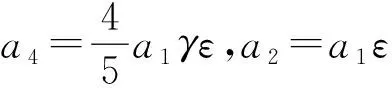
a1V1+a2V2+a3V3+a4V4-ε[a1[V3,V1]+

a2[V3,V2]+a3[V3,V3]]+a4[V3,V4]]-…=

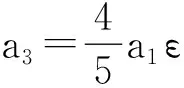
a1V1+a2V2+a3V3+a4V4-ε[a1[V4,V1]+

a2[V4,V2]+a3[V4,V3]]+a4[V4,V4]]-…=

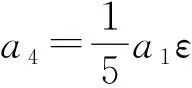
綜上,得到方程(1)的一維最優(yōu)系統(tǒng)為

{V1,V2,V3,V1+λ1V3,V1+λ2V3+λ3V4,

V1+λ4V2+λ5V3,V1+λ6V2+λ7V4},

其中λi(i=1,2,…,7)是任意常數(shù).

3 對稱約化

對稱約化是一種較為實用的約化方法.下面將會利用所求得的向量場對方程(1)進行對稱約化,從而可使方程(1)轉(zhuǎn)化為常微分方程.接下來基于第1部分的4個李點對稱,對方程(1)進行對稱約化.

1) 對于向量場

其對應(yīng)的特征方程為

由特征方程得到不變量ξ1,并且由

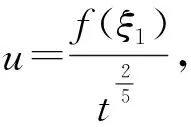
(15)

αf′f″+βf?″+γf′=0．

(16)

f′=0．

(17)

-qf′+αf′f″+βf?″+γf′=0.

(18)

至此完成了對于方程(1)的約化.

4 方程(1)的精確解

接下來將對第3部分中約化的結(jié)果進行精確解的構(gòu)造,在這里選取(16)和(18)式,但是(16)式的形式其實是(18)式中-q=0時的特殊形式,因此將選取更具有一般性的(18)式進行求解.(18)式中f是關(guān)于ξ4的函數(shù),其中ξ4=x-qt,這里的q為任意常數(shù),對(18)式關(guān)于變量ξ4積分得

(19)

其中C為任意常數(shù),取C=0.

1) 假設(shè)方程(19)有如下形式的解

(20)

這里的ω=ω(ξ4),并且滿足方程

ω″+λω′+μω=0,

(21)

這里的αm、λ、μ是任意常數(shù).由齊次平衡原理得

2(m+1)=m+4,

故m=2,則方程有如下形式的解

(22)

將(21)和(22)式代入方程(19)得

2αμ2α1α2+22βλ2μα1+120βλμ2α2+

βλ3μα1+14βλ2μ2α2+8βλμ2α1-

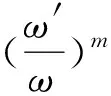
(23)

把(23)式代入(22)式,當(dāng)λ2-4μ>0時,方程(19)的精確解為

f1(ξ4)=

則方程(1)的精確解為

u1(x,t)=

當(dāng)λ2-4μ=0時,方程(19)的精確解為

則方程(1)的精確解為

u2(x,t)=

當(dāng)λ2-4μ<0時,方程(19)的精確解為

f3(ξ4)=

則方程(1)的精確解為

u3(x,t)=

其中

ξ4=x-qt,

q=βλ4-8βλ2μ+16βμ2+γ,

C1、C2、β、γ為任意常數(shù).

至此,完成了第一種輔助函數(shù)展開法對于方程(1)精確解的構(gòu)造,接下來將采用另一種輔助函數(shù)展開法對方程(1)進行研究.

2) 假設(shè)方程(19)有如下形式的解

(24)

其中ω=ω(ξ4),并且滿足方程

ω2-ω′+δ=0,

(25)

這里的αm、δ是任意常數(shù).由齊次平衡原理m=2,則方程有如下形式的解

(26)

將(25)和(26)式代入方程(19)得

136βδ2a2-4αa-2a2-αa-1a1-qa2+γa2)ω2+

16βδ2a-1+2αa-2a-1-qa-1+γa-1)+

(2αδ2a1a2-4αδa-1a2+16βδ2a1-2αα-2a1-qa1+

提取ωm的系數(shù)得到超定方程組,求解可以得到α-2、α-1、α0、α1、α1,q的值,選取以下2種情況:

(27)

(28)

(Ⅰ) 把(27)式代入(26)式,當(dāng)δ>0時,方程(19)的精確解為

則方程(1)的精確解為

當(dāng)δ<0時,方程(1)的精確解為

其中

ξ4=x-qt,q=16βδ2+γ,

C3、β、γ為任意常數(shù).

(Ⅱ) 把(28)式代入(26)式,當(dāng)δ>0時,方程(19)精確解為

則方程(1)的精確解為

當(dāng)δ<0時,方程(1)精確解為

u7(x,t)=

其中

ξ4=x-qt,q=256βδ2+γ,

C4、β、γ為任意常數(shù).

5 結(jié)束語

利用李群對一類廣義五階色散方程進行研究,求出方程的對稱,構(gòu)建了一維李代數(shù)的最優(yōu)系統(tǒng),得到約化方程,并采用2種輔助函數(shù)展開法得到方程的一系列不同的精確解,豐富了方程的精確解的種類,具有一定的理論意義,該研究方法可以應(yīng)用于其他的非線性發(fā)展方程.