基于GDE混合算法的齒輪系統輕量化設計

國瑞坤，高穎，賀磊，楊先海，李元帥，李凱

(1.山東理工大學 機械工程學院, 山東 淄博 255049；2.山東理工大學 計算機科學與技術學院, 山東 淄博 255049)

齒輪傳動系統是各領域機械的重要組成部分，在國家裝備制造業中具有不可替代的作用，其輕量化設計是所屬機械減重的重要途徑，產生的經濟效益十分可觀，是實現產品競爭力的有效途徑[1]。針對齒輪輕量化，許多學者從結構、材料、齒輪參數優化及優化方法等方面展開了討論研究。馮順利[2]通過神經網絡算法對權重系數進行調整，利用遺傳算法進行了斜齒輪參數優化，解決了優化過程中權重系數分析不合理問題。戴護民[3]運用多目標拓撲優化技術實現了齒輪輕量化設計。車林仙等[4]通過改進差分進化算法得到了更加符合實際的齒輪參數優質解。以上研究涉及改進適應度函數權重、有限元結構設計、算法離散化改進等齒輪輕量化設計方法，都取得了較好的設計結果。本文擬通過遺傳算法(genetic algorithm，GA)優化差分進化算法(differential evolution algorithm，DE)的初始種群，提出一種遺傳差分進化混合算法(GDE)并進行仿真分析，在驗證算法可行性的同時，得到更符合實際工況的輕量化齒輪系統。

1 GDE混合算法的實現

針對GA全局尋優能力強、DE局部尋優能力較差的特點，提出一種GDE混合算法，通過GA進行全局尋優，擴大搜索范圍，針對DE容易產生的局部最優解，利用GA較強的全局尋優能力，給DE提供良好的初始值，充分發揮GA與DE的優點，揚長避短，實現算法求解性能的最優化。GDE的具體運行流程如圖1所示，運行步驟說明如下：

圖1 GDE混合算法流程圖

步驟1 GA編碼并進行約束條件檢驗，隨機產生初始化種群Xn(0)。

步驟2 GA運算適應度函數采用后文介紹的目標函數1，重點考慮中心距最小問題，以獲得全局較優的種群。

步驟3 判斷是否滿足GA種群最大進化代數的終止條件。

步驟4 對種群進行選擇、交叉、變異操作，重新計算適應值，保留最優，更新產生新一代種群Xn(i)。

步驟5 得到GA算法尋優的種群Xn(i)作為DE初始值Xm(0)。

步驟6 對齒輪系統的輕量化DE適應度函數2進行定義，重點考慮齒輪系統體積最小問題，獲取更符合實際的優質解。

步驟7 判斷是否滿足DE種群最大進化代數的終止條件。

步驟8 對種群進行變異、交叉、選擇操作，重新計算適應值，保留最優，更新產生新一代種群Xm(i)。

2 齒輪系統輕量化參數優化

二級齒輪系統輕量化的主要方式有：新型輕質材料替代、拓撲結構優化、結構參數優化[5]。本文采用結構參數優化，運用上節提出的GDE算法進行輕量化設計，最終得出優化后的齒輪系統參數。二級齒輪結構簡圖如圖2所示，企業二級齒輪參數見表1。

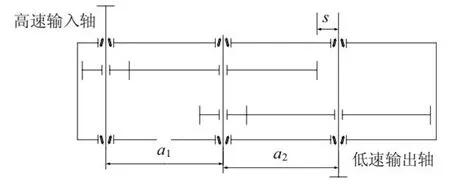
圖2 二級齒輪結構簡圖

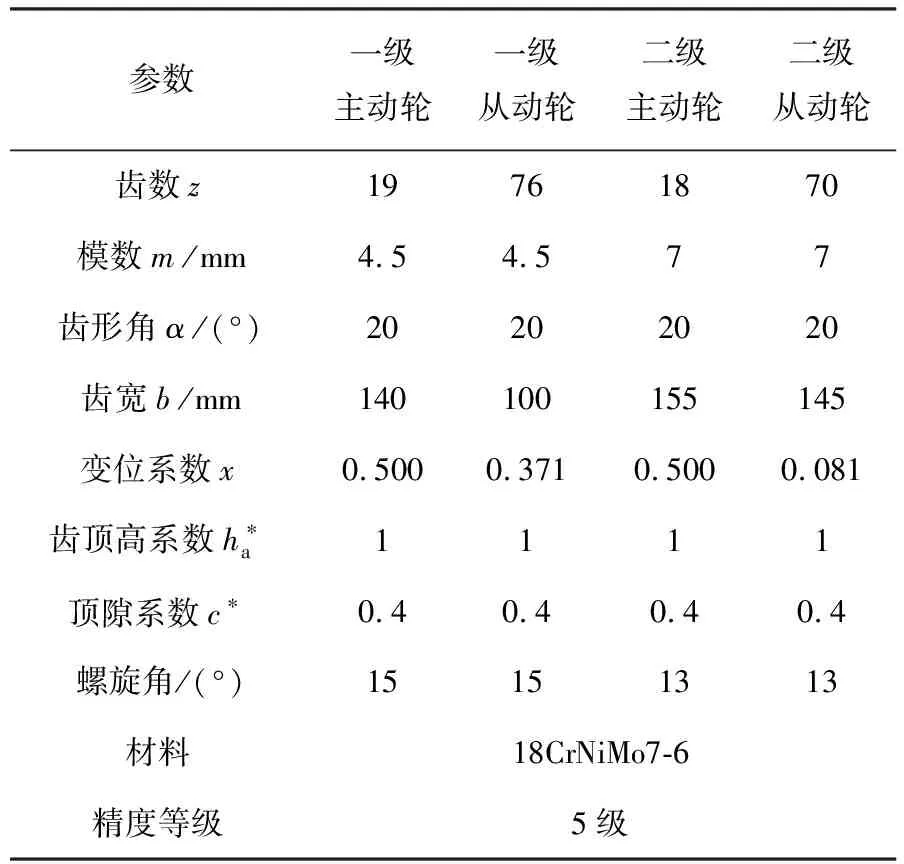
表1 企業二級齒輪系統參數

2.1 確定設計變量

由圖2可知，齒輪二級系統輕量化的設計受齒輪基本參數的影響，齒輪系統質量與中心距和體積緊密關聯，其軸向中心距尺寸由傳動比和齒輪分度圓直徑決定，齒輪系統的體積與齒寬系數以及齒根圓、齒頂圓有關。鑒于此，對齒輪相關設計變量的設計見表2。

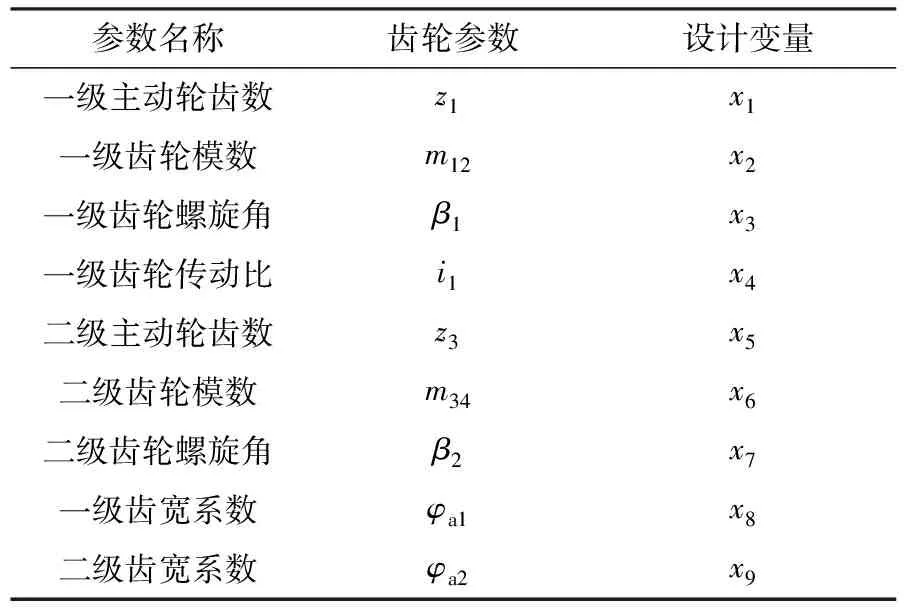
表2 二級齒輪系統輕量化設計變量

2.2 建立目標函數

齒輪二級系統的輕量化問題可以轉化為如圖2所示的中心距最小問題，即a1與a2和的最小值問題，表達式為

(1)

將目標函數1設置為

(2)

式中：i為齒輪系統總傳動比，按照企業齒輪系統參數，可知i=15.4，將目標函數1用于GA中的適應度函數。

對二級齒輪系統的體積進行計算，采用分度圓法體積計算公式[6]為

(3)

式中B為輪齒寬度，且B=φa，φ為齒寬系數，a為中心距。將目標函數2設置為

(4)

2.3 確定約束函數

結合摩擦激勵的相關影響因素，考慮齒寬、螺旋角等齒輪參數對齒面摩擦力的影響，在輕量化設計的同時對增大齒面摩擦力、增強摩擦激勵的齒輪參數加以限制；同時在輕量化設計過程中還要保持原有齒輪的齒面疲勞強度、齒根彎曲強度、幾何限制因素等特性。綜上，對輕量化齒輪系統的約束函數設置如下：

1)螺旋角約束

(5)

2)傳動比約束

(6)

3)齒寬系數約束

(7)

4)齒面接觸疲勞強度約束

(8)

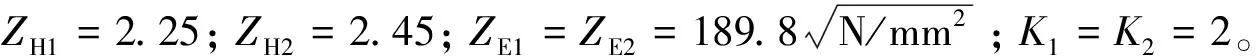
5)齒根彎曲疲勞強度約束

(9)

根據文獻[8]可得：[σF1S]=[σF2S]=714 MPa;YFa1=2.76;YFa1′=YFa2′=2.22;YFa2=2.83;Yβ1=0.875;Yβ2=0.89;YSa1=1.56;YSa1′=YSa2′=1.77;YSa2=1.54。

6)不干涉相碰約束

(10)

7)不發生齒輪根切的約束

(11)

式中αn為斜齒輪法向壓力角。

8)其他齒輪參數的約束

(12)

3 優化結果分析

對上述目標函數與約束函數進行MATLAB編程，分別運用DE、GA與編寫的GDE算法程序進行優化設計和求解運算，圓整后得到的優化結果見表3。

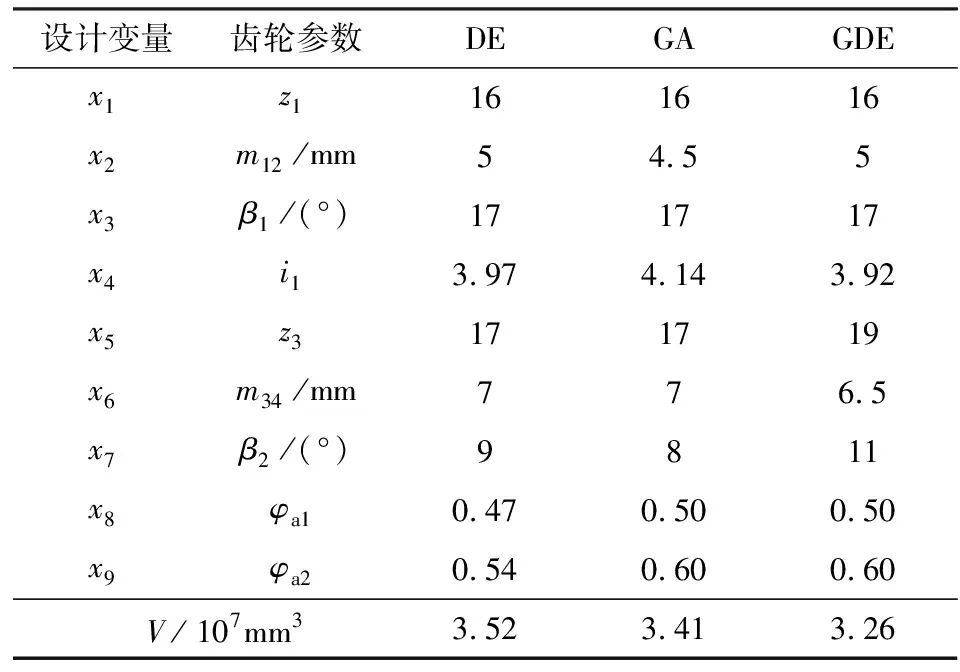
表3 各算法優化結果

3種優化算法的適應度函數、累積分布函數變化曲線如圖3、圖4所示。由圖3可知，GA在約90代時找到了最優解，DE在約40代時找到了最優解，而GDE在約20代時找到了最優解；3種方法相比較，GDE收斂速度最快且運算效率高。由圖4可知，GDE適應度函數有80%以上的解可以落到3.3×107mm3的值以內，GA適應度函數有60%以上的解可以落到3.4×107mm3的值以內，DE適應度函數有10%以上的解可以落到3.4×107mm3的值以內，說明DE容易陷入局部最優，而GA全局尋優能力強，GDE結合了兩者優勢，所得的解更優。

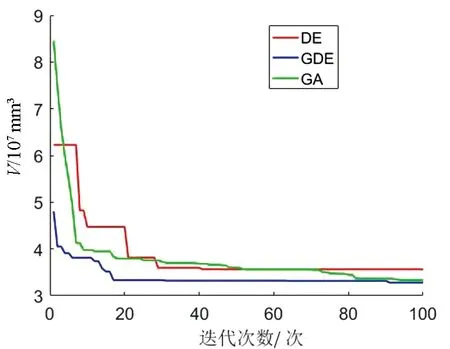
圖3 3種優化算法的適應度函數變化曲線

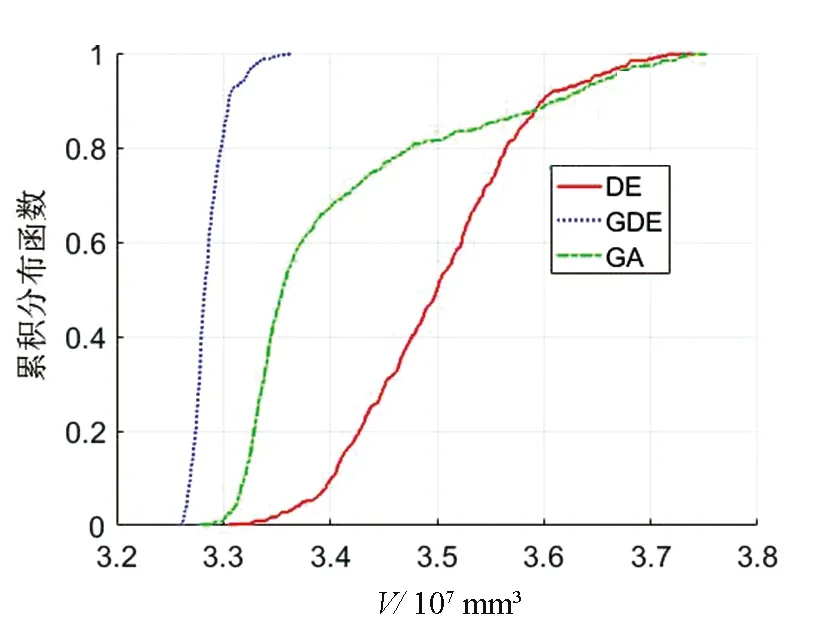
圖4 3種優化算法累積分布函數變化曲線

將各優化算法與原齒輪系統體積和重合度進行對比可知，GA優化后齒輪體積減少了6.3%，重合度增加了2.1%；DE優化后齒輪體積減少了3.3%，重合度增加了1.5%；GDE優化后齒輪體積減少了10.5%，重合度增加了5.8%。相比較其他兩種算法，GDE優化的結果更合理，效果更好。

4 模態分析

對優化后的齒輪系統進行模態分析，分析優化后固有頻率和振型的變化以及輕量化齒輪系統的振動特點和優化效果。將優化后齒輪系統模型進行簡化并導入Ansys Workbench軟件中，在Modal模塊中定義齒輪系統的幾何屬性、網格控制和圓柱約束[9]，考慮該系統的大小和實際硬件設備，設置求解階數為6階，完成求解。

模態分析中，一般前6階模態對系統的影響較大，因此本文主要針對系統前6階的固有頻率和振型進行分析。系統前6階模態振型如圖5所示，模態計算結果見表4。

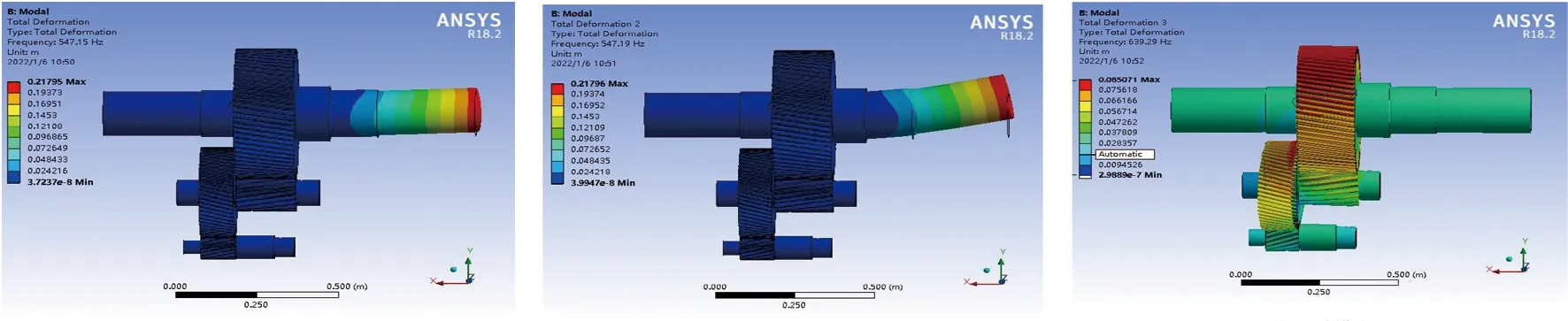
(a)第1階 (b)第2階 (c)第3階

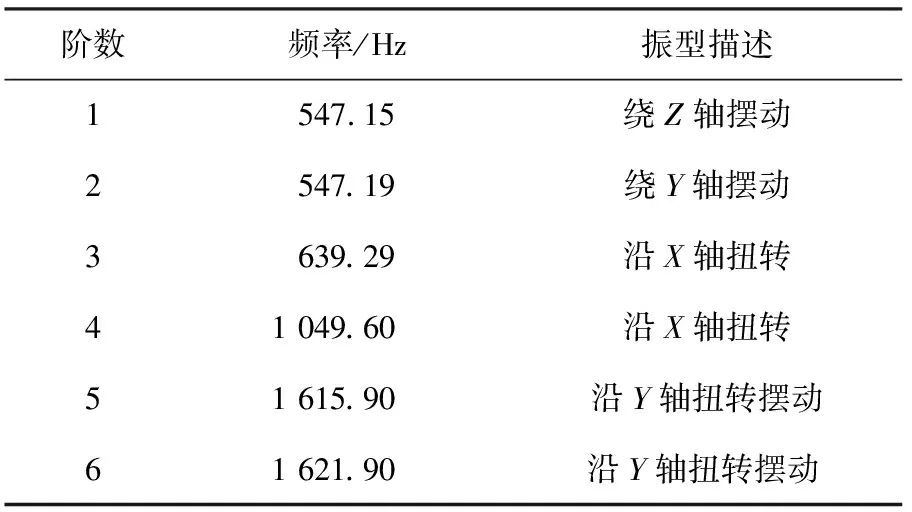
表4 優化齒輪系統前6階模態計算結果

由表4可知，齒輪系統最大頻率為1 621.90 Hz，最小頻率為547.15 Hz。由齒輪嚙合頻率的計算公式可得二級齒輪嚙合頻率為293.38 Hz,三級齒輪嚙合頻率為69.49 Hz。對比可知，與箱體振動頻率以及齒輪嚙合頻率均不重疊，不會產生共振，適用于實際工況。

5 結論

1)提出一種GDE混合算法，以兩級齒輪系統中心距與體積最小為目標進行輕量化設計，所得結果與兩種傳統方法結果進行的比較顯示，GDE收斂速度快，在20代左右即可找到最優解，GDE適應度函數有80%以上的解可以落到3.3×107mm3的值以內。

2)對GDE算法進行的編程仿真結果表明，GDE優化后齒輪體積減少了10.5%，重合度增加了5.8%。

3)對輕量化后齒輪系統進行建模和模態分析，仿真結果顯示輕量化后齒輪不會產生共振，符合實際工況需求。