X射線脈沖星導航方法研究綜述

鄭偉，王禹淞，姜坤，王奕迪

1．國防科技大學 空天科學學院，長沙 410073 2．北京跟蹤與通信技術研究所，北京 100094

脈沖星是一種高速旋轉的中子星，是大質量恒星在其生命末期引發超新星爆炸的產物［1］。如圖1所示［2］，脈沖星的自轉軸與磁軸不重合，其兩個磁極同時向外輻射電磁輻射束。當脈沖星的輻射束掃過觀測者時，觀測者就可以接收到來自脈沖星的信號，就如同海上航行的船舶接收燈塔的信號一樣。因此，脈沖星也被稱作“宇宙中的燈塔”。脈沖星的自轉周期具有極好的長期穩定性，一些毫秒脈沖星的穩定性可以與原子鐘相媲美。另外，脈沖星在許多情況下可以同時在不同波段被觀測到，如光學、射電、X射線和γ射線等［3］。由于X射線輻射很容易被小面積的探測器探測到，可以利用脈沖星輻射的X射線信號進行航天器自主導航，這種導航方式被稱作X射線脈沖 星 導 航（X-ray Pulsar-based Navigation， XPNAV）。

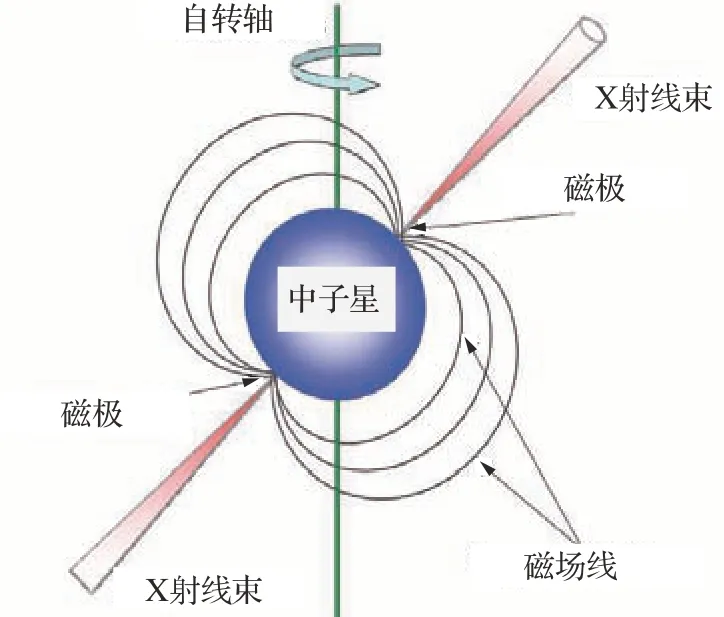
圖1 脈沖星的自轉模型［2］Fig. 1 Rotation model of pulsar［2］

與目前主要通過測量天體方向信息的天文導航相比，X射線脈沖星導航利用了脈沖星的時間信息，因此其導航性能受脈沖星與航天器之間距離的影響較小。與衛星導航相比，X射線脈沖星導航適用于近地和深空，不受人為的干擾。另外，由于利用了脈沖星的時間信息，X射線的脈沖星導航可以實現3種不同于其他自主導航方法的應用：①時間基準的自主維持。在航天器自主運行過程中，星載原子鐘用于為航天器提供定時信息。然而，星載原子鐘不可避免的頻率漂移可能會對航天器的正常運行造成影響。NICER團隊的研究結果顯示，對X射線脈沖星進行2年的觀測，脈沖星時間穩定度可以達到10?14量級［4］。在現有觀測水平下，如果對X射線脈沖星進行3年以上的觀測，有望實現10?15～10?16量級的穩定度，這與最佳原子鐘的長期穩定性相當［5］。因此，脈沖星可作為自然時間基準，用于削弱星載原子鐘的誤差。②衛星星座的自主導航：衛星星座的自主導航目前能通過星間鏈路來實現。然而，星間鏈路只能地確定一個星座內衛星的相對位置，不能抵抗整個星座的旋轉。在這種情況下，脈沖星可以被視為天然的“錨”，在慣性坐標系中為整個衛星星座提供絕對方向參考。與以前的地面“錨”方法相比，基于脈沖星的方法可以完全消除人為干擾。③深空探測器自主導航：目前在太陽系內可用的自主導航方法主要是基于星光角距的導航方法，該方法的導航精度受航天器與近天體距離的影響較大。處于巡航段的深空探測器，由于與近天體距離較遠，星光角距導航方法只能提供幾千公里左右的定位精度。相比之下，X射線脈沖星導航通過處理脈沖星的時間信息來實現導航。如果脈沖到達時間的精度高于0.1 ms，則很容易實現優于30 km定位精度［5］。因此，X射線脈沖星導航可以為深空探測器提供精確的導航定位服務。

近些年，國內外完成了多次脈沖星導航的飛行試驗，2018年，美國的SEXTANT （Station Explorer for X-ray Timing and Navigation Tech?nology） 項目組利用搭載在國際空間站上的NICER探測器成功驗證了脈沖星導航，并實現了優于10 km的導航精度［6］。中國在脈沖星導航飛行試驗方面也取得了很多成果：多個團隊分別利用天宮二號上的POLAR探測器［7］、慧眼衛星［8］以及XPNAV-1衛星（圖2）的［9-12］實測數據，初步驗證了脈沖星導航的可行性。未來，脈沖星導航將逐步走向工程實踐。

圖2 XPNAV-1［12］Fig. 2 XPNAV-1［12］

圖3給出了脈沖星導航的原理框圖。可以看出，航天器搭載的X射線探測器接收脈沖星輻射的X射線光子，并利用星載原子鐘記錄下光子到達探測器的時間。接下來，根據光子到達探測器的時間推算出光子到達太陽系質心（Solar Sys?tem Barycenter， SSB）的時間。而后，通過脈沖星數據處理算法，從一系列的光子到達時間中解算出脈沖到達時間（Time of Arrival， TOA）。最后，結合導航定位算法求解出航天器的位置和速度。因此，脈沖星導航的關鍵在于如何從微弱的脈沖星光子數據中提取出脈沖TOA，以及如何通過脈沖TOA解算出航天器的位置速度信息。

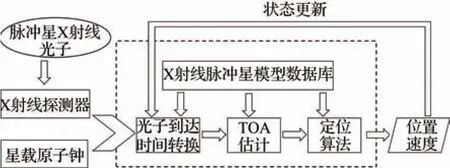
圖3 脈沖星導航原理框圖Fig. 3 Flow chart of pulsar navigation

隨著脈沖星導航理論研究與工程實踐的發展進步，脈沖星導航方法的研究逐步從概念提出、理論體系構建，向解決實際工程實現中遇到的如測量噪聲、系統誤差以及計算復雜度等問題的方向發展。針對X射線脈沖星導航中的數據處理、導航理論以及應用體制進行了全面的梳理與總結，全文具體安排如下：① 介紹了X射線脈沖星導航的背景意義，梳理了脈沖星導航需要解決的主要問題；② 對脈沖星導航的研究現狀進行了詳細梳理，包括面向導航的脈沖星數據處理技術、脈沖星導航理論；③ 系統歸納了X射線脈沖星導航的應用體制；④ 提出當前研究存在的主要問題并對其后續發展進行展望，為中國X射線脈沖星導航技術發展提供參考。

本文主要側重于理論方法，因此不涉及X射線探測器的進展，但在方法的評述中會考慮到X射線探測器的特點。

1 面向導航的X射線脈沖星數據處理

脈沖星信號非常微弱，在軌運行的航天器無法記錄到連續的脈沖信號，只能記錄一系列脈沖星光子到達時間。因此，需要采用脈沖星數據處理技術處理脈沖星光子到達時間序列，得到對導航有用的信息。針對不同的應用階段，脈沖星數據處理分別需要解決不同的問題。在數據庫構建階段，脈沖星數據處理主要用于構建高精度的脈沖星模板輪廓。在脈沖星導航在軌工作階段，脈沖星數據處理主要用于獲取脈沖TOA。

1.1 脈沖星信號模型

脈沖星光子到達探測器的事件{tk}N k=1服從非齊次的泊松分布，在時間段(ta，tb)內，有k個光子到達探測器的概率為［13］

式中：α、β分別為脈沖星的流量和背景噪聲。h為歸一化的脈沖輪廓，圖4給出了美國SEXTANT項目數據庫中6顆脈沖星的輪廓［14］。

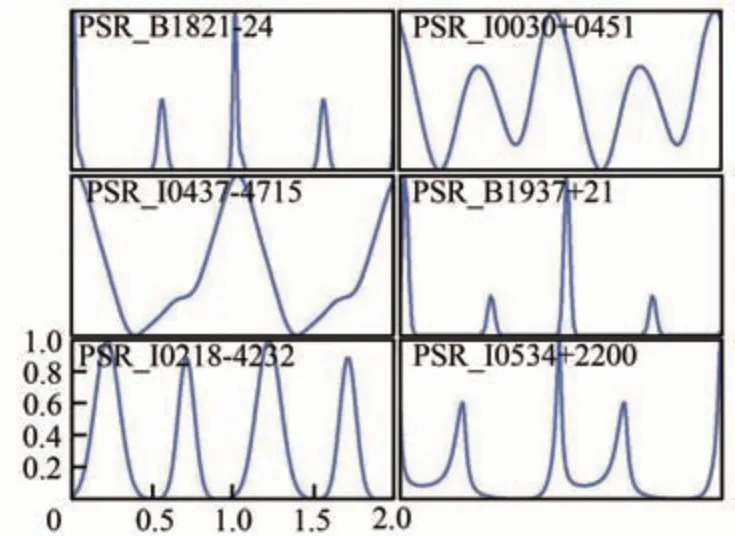
圖4 SEXTANT 數據庫中的脈沖星模板輪廓（2個周期）［14］Fig. 4 Template profiles of pulsars for SEXTANT catalog （two cycles） ［14］

?det(t)為探測器在t時刻探測到的脈沖相位，可表示為［15］

式中：?0為脈沖星信號在t0時刻的相位（即初相）；fs為該脈沖星信號的頻率；n為脈沖星方向矢量；v為航天器的速度矢量。

1.2 模板構建

脈沖星的模板輪廓是整個脈沖星數據處理過程中的基準信息。因此，高精度的脈沖星模板輪廓對于脈沖星數據處理乃至脈沖星導航的順利進行具有至關重要的作用。針對脈沖星模板構建中的2類關鍵技術——脈沖星周期搜索技術和脈沖星信號降噪技術的研究進展進行簡要介紹。

1.2.1 脈沖星周期搜索

脈沖星周期搜索是從一系列的脈沖星光子中計算脈沖星信號周期fs的技術。準確的脈沖星周期是構建高精度脈沖星模板的基礎。

由于脈沖星光子到達時間的記錄不均勻，無法直接利用經典傅里葉變換來計算脈沖星的周期。為此，針對光子到達時間的非均勻采樣問題，學者們研究了Lomb-scargle周期譜［16-17］、弦長法［18-20］、自相關法［21-22］等經典的脈沖星周期搜索方法。

經典的脈沖星周期搜索方法可有效解決光子到達時間非均勻采樣的問題，但是還存在計算精度不高、計算量較大等問題。近些年，學者們在經典脈沖星周期搜索方法的基礎上進行了一定改進。Huijse等將信息準則引入周期搜索，提出了基于相關熵譜的周期搜索方法［23］，該方法的周期搜索性能較經典方法有所提升，但是存在核寬度不能自適應調整的問題。周慶勇等在Lomb-scargle法的基礎上進行了改進，仿真數據計算結果表明，改進的Lomb-scargle法相比原有算法的計算速度有所提高［24］。李建勛等基于脈沖星信號的平穩相關模型，提出了基于相關方差的脈沖星周期搜索方法，該方法對數據量的要求較低，但不適用于處理非連續的脈沖星觀測數據［25］；張華和許錄平基于脈沖星累積輪廓與其周期之間的相關性，提出了基于最小熵的脈沖星周期搜索方法［26］。

上述的幾種脈沖星周期搜索方法均需要使用不同的周期進行脈沖星輪廓的折疊，當需要處理的脈沖星數據量較大時，算法的計算量會明顯增加，極大的增加了計算負擔。為了解決這一問題，人們開始研究高效的脈沖星周期搜索方法。張新源等提出使用改進的快速折疊算法，恢復多個周期的折疊輪廓，提高了周期搜索的效率，但該方法僅適用于流量較高的脈沖星［27］。宋佳凝根據周期的誤差與脈沖TOA估計結果的關系，提出了基于TOA信息的脈沖星周期估計方法。該方法利用帶誤差的初始周期連續解算出一系列脈沖TOA，而后基于最小二乘法直接解算出初始周期的誤差，進而求解出脈沖星信號的周期［28］。Liu等基于脈沖星信號的稀疏特性，提出了基于壓縮感知的脈沖星周期搜索方法［29-30］，該類方法有效降低了周期搜索的計算量，但是對周期的初始誤差和脈沖星的觀測時長存在一定的限制。目前，脈沖星周期搜索的主要難點是如何平衡計算速度與周期搜索的精度，以及方法的適應性問題。

1.2.2 脈沖星輪廓構建技術

通過周期搜索確定脈沖星的周期后，可通過歷元折疊法得到脈沖星模板輪廓。歷元折疊法的基本原理為：假設探測器觀測脈沖星的時間為Tobs，觀測時間內包含NP個脈沖星周期P，因此有Tobs≈NP·P。周期P可劃分為Nb個bin塊，每個bin塊的長度為Tb。把探測器探測到的光子到達時間統一折回到第一個周期，統計每個bin塊中的光子數，將每個bin塊中的光子數進行歸一化，從而得到脈沖輪廓［31］。在第i個bin塊，i∈[1，Nb]的歸一化輪廓(Ti)可表示為［30］

式中：cj為第j個周期的第i個bin塊內的光子數；Ti為第i個bin塊的中心對應的時刻。

圖5給出了歷元折疊法的示意圖。從圖中可以看出，通過歷元折疊法獲得的脈沖星輪廓質量受bin塊數的影響。為獲得較高精度的模板輪廓，需要較大的bin塊數；然而，當bin塊數較多時，獲得的模板輪廓會引入較多的噪聲，導致“毛刺”較多。此時，需要采用脈沖星信號降噪技術，獲得較為平滑的高精度脈沖星模板輪廓。

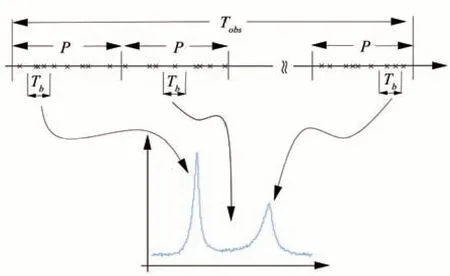
圖5 歷元折疊法示意圖Fig. 5 Schematic diagram of epoch folding method

經典的脈沖星信號降噪方法主要有2類：①對恢復的脈沖輪廓，利用高斯函數進行擬合［32］；②利用小波變換和經驗模態法對恢復的脈沖輪廓進行降噪［33-34］。其中，第1類基于高斯函數擬合的方法需要事先確定高斯函數的基本參數，且對脈沖星信號的信噪比及光子量有較高的要求。同樣，第2類基于小波變換和經驗模態的脈沖星信號降噪方法也存在小波基、分解層數及本征模函數的選擇問題［35-36］，對專家的經驗依賴較高。對于處理不同的脈沖星輪廓，難以建立統一的模型。

為了解決這一問題，Wang等提出了基于核回歸的降噪方法，由于核回歸采用了非參數模型，且可通過交叉驗證來自適應調整核寬度，因此該方法具有較高的自主性，對人為經驗的依賴較小［37］。另一方面，根據文獻［37］的分析，與小波變換和經驗模態法相比，基于核回歸的降噪方法降噪后的輪廓引入的相位偏差最小。上述方法本質上是通過歷元折疊法獲得低分辨率模板輪廓，而后利用核回歸獲得高分辨率的模板輪廓。宋佳凝在傳統核回歸方法的基礎上提出直接利用光子到達時間序列構造模板輪廓的方法［28］。分析表明，利用該方法構造的模板可有效提高脈沖TOA的估計精度［28］。

1.3 在軌數據處理

脈沖TOA是脈沖星導航的基本測量量。然而，由于脈沖星信號十分微弱，航天器無法接收到完整的脈沖信號，也就無法直接記錄脈沖TOA。根據文獻［15］，脈沖到達SSB處的時間可由在該點建立的時間相位模型進行計算，脈沖星的時間相位模型可表示為對脈沖星的相位?在t0時刻進行泰勒展開，具體形式為［15］

式中：t0為參考歷元時刻；?(t0)為t0時刻的脈沖星相位；f(n)為脈沖星自轉頻率的導數，n為階數。通過時間相位模型可以計算出t時刻脈沖星的相位。同樣，若脈沖星信號相位已知，也可推算出其到達SSB的時刻。因此，可通過解算某一時刻tSC航天器接收到的脈沖星信號的相位?(tSC)。進一步，根據?(tSC)可以解算出該信號到達SSB的時刻tSC，2個tSC之差，即反映了航天器在脈沖星方向上相對于SSB的距離之差。因此，脈沖TOA的求解問題，可轉化為脈沖相位的求解。

此外，由于航天器做軌道運動，其在軌觀測到的脈沖星信號耦合了軌道運動產生的影響，因此需要解決考慮航天器運動情況下的脈沖相位提取，即研究脈沖星在軌數據處理方法。本節首先介紹不考慮航天器軌道運動的脈沖相位估計方法，而后詳細介紹考慮航天器軌道運動的脈沖星在軌數據處理方法所面臨的問題及研究進展。

1.3.1 不考慮航天器運動的數據處理

假設航天器靜止或沿脈沖星方向作勻速直線運動，有兩類脈沖相位計算方法：基于歷元折疊的方法［30］和直接利用光子到達時間的方法［38］。

歷元折疊法的原理在1.2.2節中已經介紹，通過歷元折疊法，可恢復脈沖輪廓。而后，通過互相關法、非線性最小二乘法和快速近最大似然估計等方法將恢復輪廓與事先建立的模板輪廓對比，即可估計出脈沖相位。由于該類方法需要首先通過歷元折疊恢復脈沖輪廓，若脈沖星信號的周期不準確，將會影響歷元折疊的效果，進而影響脈沖相位的估計精度。因此，在使用該類方法之前，必須先進行周期搜索。

直接利用光子到達時間的方法又稱作極大似然法。該方法不需進行歷元折疊，而是利用光子到達時間的隨機特性導出的對數似然函數，通過最大化似然函數計算脈沖星信號的相位和周期。若不考慮航天器運動，可將式（3）簡化為

根據式（1），在時間段(ta，tb)，光子到達事件的聯合概率密度函數可表示為

將式（7）定義為似然函數，對其取自然對數可以得到

當探測器觀測脈沖星的時間足夠長時，式中的第二項可以認為是一個常數。因此參數?0和fs可以通過求解如下的優化問題來計算

基于歷元折疊的方法實現簡單且計算量較低，但計算精度略低；直接利用光子到達時間的方法精度較高，但計算量隨光子數量的增加而明顯增加。此外，針對短時間的脈沖星觀測數據難以得到較好的脈沖相位估計結果，文獻［39］提出利用先驗信息，在極大似然法的基礎上建立了基于極大驗后的脈沖相位估計準則，有效提高了短觀測時間情況下的脈沖相位估計精度。

1.3.2 考慮航天器運動的在軌數據處理

由式（3）可知，對于在軌運動的航天器，由于航天器精確位置、速度未知，而航天器運動會引入非線性時變的多普勒頻率，導致航天器接收的脈沖星信號發生畸變。因此，傳統的基于歷元折疊的方法和極大似然估計的方法不適用于在軌計算脈沖相位。為此，Golshan和Sheikh提出了一種相位跟蹤算法來估計脈沖到達時間和時變的脈沖星信號的頻率［40］。該方法將航天器的軌道近似為分段線性模型，以保證每個分段內的脈沖星頻率可以近似為常數。然后，利用成熟的方法可以很容易地估計每一塊的脈沖星信號的相位和頻率。最后，采用數字鎖相環（Digital phase-locked loop， DPLL）來跟蹤分段間頻率的變化。黃良偉等提出DPLL可以利用濾波的方法實現對脈沖星信號的相位和頻率的跟蹤，該方法降低了原有方法的計算量，并且克服了DPLL不能很好應對信號噪聲的問題［41］。

上述2種方法都是基于航天器軌道可有效近似為分段線性定常系統的假設。因此，上述2類方法可統一稱為分段線性定常模型法。該類方法奏效的必要條件是：在每個間隔內，可以通過光子到達時間序列獲得可靠的脈沖星初相和頻率的可靠估計結果。雖然足夠短的間隔劃分可以有效保證分段線性定常模型高精度近似真實航天器軌道，但間隔劃分太短，會導致脈沖星初相和頻率的估計結果不可靠。將可以保證估計結果可靠的間隔時間稱為門限時間，對于不同流量的脈沖星，其門限時間不同。PSR B0531+21等高流量脈沖星的門限時間一般小于1 s，而1 s的間隔時間長度已能夠成功保證分段線性定常模型可高精度近似于真實航天器軌道。但是，高流量脈沖星為年輕脈沖星，存在自轉頻率不穩定、計時噪聲大等問題。相比而言，毫秒脈沖星的自轉頻率高度穩定，鮮有周期躍變現象，是較為理想的導航信號源。對于毫秒脈沖星PSR B1821-24而言，該脈沖星的門限時間會達到100 s左右。對日心巡航等軌道角速度小的軌道而言，100 s間隔時間引起的分段線性定常模型的近似誤差可以忽略。而對近地軌道等軌道角速度大的軌道而言，100 s間隔時間引起的分段線性定常模型近似誤差會產生難以忽略的脈沖星信號相位估計誤差，從而導致后續DPLL或跟蹤濾波的結果有偏，降低脈沖相位的計算精度。

為了滿足微弱脈沖星的在軌數據處理問題，王奕迪等將航天器的位置引入脈沖星的相位傳播模型，并利用航天器的軌道動力學信息對傳播模型進行線性化［42］。與以往的相位跟蹤算法相比，該方法不需要將航天器的軌道近似為分段常數模型，因此可以用于信號微弱的毫秒脈沖星數據處理。

基于王奕迪提出的線性化脈沖相位傳播模型，脈沖星在軌數據處理問題可采用傳統的歷元折疊法或極大似然法進行求解［42-43］。張大鵬在基于χ2搜索的歷元折疊法的基礎上，提出了指標函數再估計的方法，相比于原有方法相位估計精度提高了近1倍［44］，如圖6所示。Wang等在極大似然法的基礎上，提出了基于CE-Adam算法的脈沖星在軌數據處理方法，極大提高了原有方法的計算效率，但仍存在計算結果的隨機性問題［45］。文獻［44-45］在研究脈沖星在軌數據處理問題時，采用了脈沖星試驗01星、“慧眼”衛星以及NICER探測器的實測數據對方法進行了驗證。相比于仿真數據，實測數據中包含了未建模的空間輻射的影響，更能反映數據處理方法在真實導航場景中的性能。

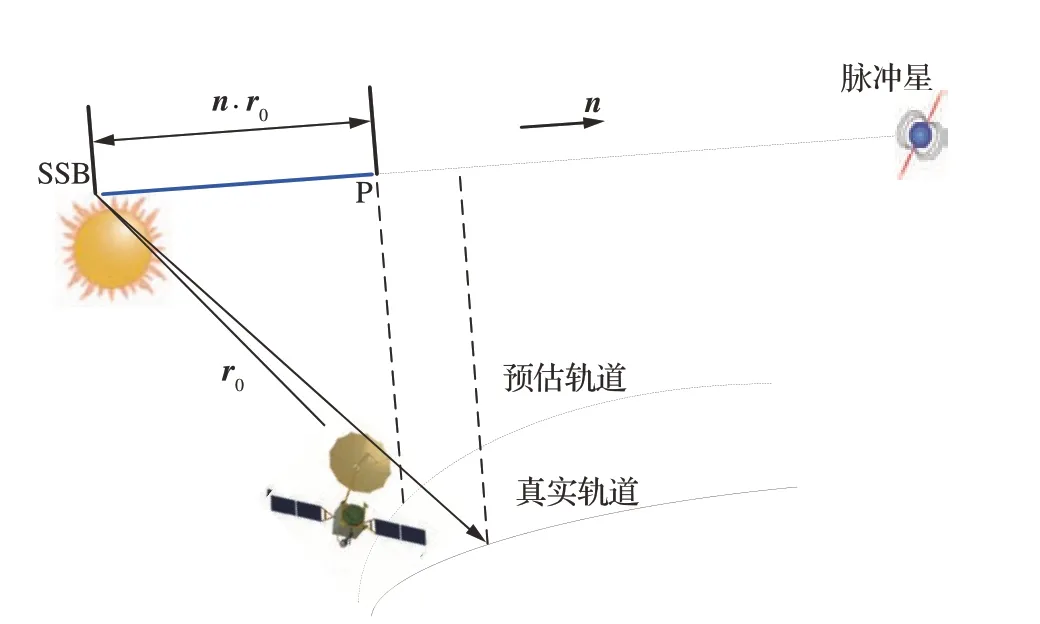
圖6 在軌信號處理示意圖［44］Fig. 6 Schematic diagram of on-board data processing［44］

2 脈沖星導航理論

到目前為止，X射線脈沖星導航理論的發展經歷了3個階段。

1）概念提出階段（1971—1981年）。1971年，Reichley等首先提出了射電脈沖星可以用于導航的想法［46］。1974年，Downs研究了一種使用射電脈沖星的行星際導航方法，概算出定位精度可以達到150 km左右［47］。然而，為了實現這一目的，航天器必須裝載直徑至少為25 m的射電望遠鏡，并持續觀察脈沖星24 h。由于X射線輻射易于被小型探測器探測到，Chester和Butman于1981年首次提出了利用X射線脈沖星進行航天器導航的概念［48］。

2）初步形成階段（1981—2005年）。Wood建議建立一個X射線導航系統，為航天器提供位置、姿態和時間確定服務［49］。2004年，歐空局分析了X射線脈沖星導航和脈沖星信號模型的基本原理，探討了脈沖星導航工程實現的可行性［50］。此后，Sheikh為脈沖星導航做出了一系列貢獻。他廣泛調查了與脈沖星導航相關的技術，建立了一個導航脈沖星數據庫，提出了一個考慮Romer延遲、Shapiro延遲和視差的時間轉換模型［2］。Sheikh的工作標志著脈沖星導航理論初步成型。

3）改進完善階段（2005年至今）。隨著脈沖星導航理論研究逐步成型，國內外相繼進行了X射線脈沖星導航飛行試驗。在已進行的飛行試驗中，美國的SEXTANT團隊通過觀測3顆毫秒脈沖星實現了脈沖星導航的驗證，中國的POLAR探測器、XPNAV-1衛星（圖7）和“慧眼”衛星由于探測器體制和有效面積的限制，僅能觀測到大流量的Crab脈沖星，因此采用單脈沖星導航體制實現了脈沖星導航。通過飛行試驗不僅獲得了寶貴的脈沖星在軌觀測數據，而且在工程實踐中也發現了如數據處理效率、導航算法穩定性等問題。因此，針對飛行試驗的實際工程需求，并依據在飛行試驗中獲得脈沖星實測數據，學者們對脈沖星導航方法進行了一系列的改進和完善。

圖7 XPNAV原理示意圖Fig. 7 Schematic diagram of XPNAV

2.1 系統誤差補償

系統誤差是影響X射線脈沖星導航精度的重要因素之一。以脈沖星角位置誤差為例，若脈沖星角位置存在1 mas的誤差，會使得導航系統產生約700 m的位置估計偏差［14］。因此，對系統誤差進行分析和補償是提高脈沖星導航精度的重要手段，也是國內外學者研究的熱點。X射線脈沖星導航主要的系統誤差及誤差的影響形式如表1所示。

表1 XPNAV主要系統誤差Table 1 Main systematic errors of XPNAV

在系統誤差的分析方面，Graven將脈沖星導航系統的誤差因素分為信號源模型誤差、敏感器誤差、信號源測量誤差、航天器系統誤差以及其他模型誤差等，并初步分析了脈沖相位誤差對測量信息的影響［51］。孫守明等對星載原子鐘鐘差進行建模，并指出通過同時觀測四顆脈沖星可實現利用脈沖星同步進行定位和授時［52］。

在系統誤差補償方面，目前主要有2類方法：擴展狀態法和歷元差分法。

在擴展狀態法方面，Liu等對脈沖星角位置誤差的影響進行建模，并采用擴展狀態同步估計法，削弱了該誤差項的影響［53］。Wang等分析了天體星歷誤差對脈沖星導航觀測模型的影響，提出了削弱天體星歷誤差影響的方法［54］。王璐等提出將鐘差和方位誤差造成的系統偏差作為增廣狀態，提出了修正鐘差和方位誤差的脈沖星導航方法［55］。武瑾媛等將火星和地球對探測器引力作用影響的差值作為增廣狀態法引入到火星探測器編隊的相對導航中，有效修正了模型誤差，提高了導航精度［56］。

在歷元差分法方面，Wang等提出了基于歷元差分的脈沖星導航系統誤差綜合補償方法［57］。針對單星序貫觀測脈沖星的導航方式，鄭偉等提出了跨歷元差分法，可有效削弱系統誤差對單探測器脈沖星導航的影響［58］。寧曉琳等將擴展狀態法與歷元差分法結合，提出了基于脈沖TOA與相鄰歷元間的TOA之差（Time Differential TOA， TDTOA）的擴展狀態法，該方法集合了擴展狀態法和歷元差分法的優勢，相比于僅使用TOA的擴展狀態法和僅使用TDTOA的歷元差分法，可更加有效抑制系統誤差的影響［59］。

擴展狀態法和歷元差分法法均可削弱系統誤差的影響。歷元差分法的收斂速度比擴展狀態法快，且不需要計算高維矩陣。因此，歷元差分法更適合用于X射線脈沖星導航的系統補償中。

2.2 濾波方法

如圖3所示，在獲取脈沖TOA之后，需要通過定位算法求解出航天器的位置、速度等導航信息。其中，濾波方法是脈沖星導航中最常用的定位算法。濾波算法通常將航天器的軌道動力學模型作為狀態方程，以X射線探測其的測量模型為測量方程，估計出航天器的位置、速度等狀態信息。

由于航天器的軌道動力學模型為典型的非線性模型，多數學者在傳統擴展卡爾曼濾波（Ex?tended Kalman Filter， EKF）和無跡卡爾曼濾波算法（Unscented Kalman Filter， UKF）等非線性濾波算法的基礎上，結合脈沖星導航的特點進行相應的改進。針對方差不確定下星歷表誤差的影響，褚永輝等提出了出一種基于方差匹配的自適應濾波方法，削弱了不確定項對觀測的影響［60］。針對傳統EKF方法不能克服不確定性參數以及乘性噪聲等缺陷，李敏等提出了魯棒EKF濾波算法［61］。針對脈沖星導航過程中可能出現異常觀測量的情況，姜宇等提出了一種改進的無跡卡爾曼濾波導航濾波算法，可削弱異常觀測量的影響［62］。為解決傳統EKF在脈沖星導航過程中易發散的問題，胡騰戈和武迪利用記憶衰減濾波控制誤差發散，提高了濾波算法的穩定性［63］。魏二虎等提出了自適應擴展卡爾曼濾波（Adap?tive Extended Kalman Filter， AEKF）算法，該方法可有效克服濾波初始狀態偏差的影響，較快地獲得與傳統EKF相當精度的狀態估計結果［64］。針對濾波器參數的選取對狀態估計精度影響的問題，熊凱等提出了Q學習擴展卡爾曼濾波器（Qlearning extended Kalman filter， QLEKF），利用Q學習的決策能力，自適應地選擇濾波器參數，從而改善狀態估計性能［65］。

基于EKF算法和UKF算法，學者們處理了脈沖星試驗01星和“慧眼”衛星的觀測數據，均獲得了較好的定軌結果，驗證了X射線脈沖星導航的可行性。丁陶偉等使用脈沖星試驗01星的觀測數據，采用EKF算法實現了脈沖星試驗01星的自主定軌［9］。張大鵬等利用“慧眼”衛星的觀測數據，采用UKF算法，通過與衛星精密定軌星歷對比，驗證了約10 km的脈沖星導航精度［66］。

此外，還有學者將魯棒濾波、信息濾波等新型濾波算法應用于X射線脈沖星導航中。Xiong等推導了非線性魯棒濾波，并成功應用于X射線脈沖星導航來抑制脈沖星角位置誤差、脈沖星距離誤差的影響［67］。為解決拖尾測量噪聲對濾波算法精度的影響，Wang等提出了基于最大相關熵準則的無跡信息濾波器，有效抑制了拖尾噪聲的影響，同時克服了傳統穩健濾波需要將非線性模型線性化的缺陷［68］。針對脈沖星組合導航中各觀測量采樣周期不同的問題，Wang等提出了動靜態濾波方法，可有效避免大采樣率信息的丟失，也適用于強非線性的情況［69］。為克服有色噪聲以及中心天體星歷誤差的影響，許強等設計了兩級強跟蹤差分濾波器，有效提升了導航性能［70］。

3 脈沖星導航應用體制

為擴展脈沖星導航的應用范圍，針對脈沖星導航的特點，國內外學者進行了脈沖星導航應用體制的研究，從以脈沖星為主的組合導航、脈沖星導航在近地空間的應用以及脈沖星導航在深空探測中的應用3個方面進行論述。

3.1 以脈沖星為主的組合導航

由于脈沖星信號較弱，為獲得可靠的脈沖TOA，需要對脈沖星進行較長時間的觀測，這也就導致了脈沖星導航的信息更新較慢，限制了脈沖星導航的應用。為了解決這一問題，可以通過將脈沖星導航與其他更新頻率較快的導航方式進行組合，從而實現兼具精度與實時性的組合導航系統。

目前，常用于與脈沖星導航進行組合的導航方式主要是慣性導航和光學導航。在脈沖星/慣性組合導航方面：孫守明等研究了針對近地軌道航天器的脈沖星/慣性組合導航的可行性，該組合導航系統可有效提高僅依靠脈沖星的導航系統的適用范圍并削弱慣性導航誤差隨時間累積的問題［71］。此外，還研究了利用擴展狀態法削弱星載原子鐘鐘差對脈沖星/慣性組合導航的影響［72］。

在脈沖星/光學組合導航方面：Liu等針對近地軌道航天器，提出了脈沖星/星光角距以及脈沖星/太陽多普勒的組合導航方法［73-74］。Li等提出了針對木星轉移段的脈沖星/光學組合導航方法［75］。楊博等提出了基于虛擬觀測值的單脈沖星/星光的組合導航方法，該方法在脈沖星觀測周期內使用由神經網絡生成的虛擬觀測值與星光角距測量量進行集中濾波，一定程度上提高了導航精度［76］。針對編隊飛行航天器，喻子原等提出了脈沖星/天文多普勒差分的組合導航方法［77］。Wang等對脈沖星/傳統天文組合導航方法進行了詳細的研究，分析了最佳的信息融合方式，并分別以近地高軌航天器和深空探測器的自主導航任務分析了導航系統的性能［78-79］。此外，王宏力等將X射線脈沖星導航、慣性導航與星光導航三者組合，提出了用于彈道導彈的單脈沖星/慣性/星光組合導航方法［80］。針對深空小推力探測器的自主導航任務，Wang等提出了X射線脈沖星/慣性/星光的組合導航方式［81］。

在上述組合導航方法中，脈沖TOA是獨立解算的，根據1.2節的介紹，使用現有方法解算脈沖TOA的計算量巨大，難以保證導航的實時性。為了提高脈沖TOA的解算效率，Wang等提出了脈沖星/星光多普勒深組合導航方法，將星光多普勒測量信息應用于脈沖TOA的解算中，提供了更深層次的脈沖星組合導航思路［82］。此后，Wang等分別研究了脈沖星/光學/星光多普勒深組合、脈沖星/星光角距深組合導航方法，拓展了以脈沖星為主的深組合導航思路［83-84］。以脈沖星/星光角距組合導航為例，圖8和圖9分別給出了傳統脈沖星/星光角距組合導航方案和脈沖星/星光角距深組合導航方案，相比于傳統的組合導航方法，深組合導航將測量信息用于脈沖TOA的估計中，可有效降低估計脈沖TOA的計算量。

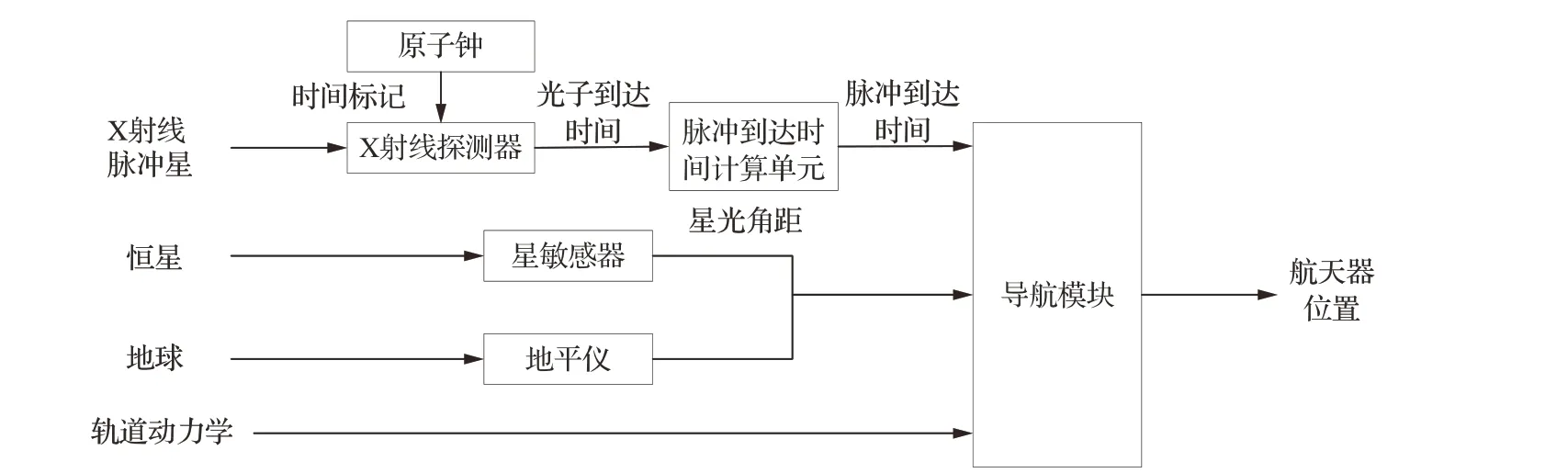
圖8 傳統脈沖星/星光角距組合導航Fig. 8 Pulsar/ stellar angle integrated navigation

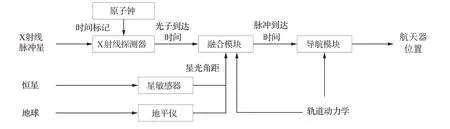
圖9 脈沖星/星光角距深組合導航Fig. 9 Pulsar/ stellar angle deeply integrated navigation

3.2 脈沖星導航在近地空間的應用

目前，近地空間的航天器主要依靠全球衛星導航系統、天文導航及地面測控系統等獲得導航服務。X射線脈沖星導航在導航精度、探測器體積功耗等方面并不具備絕對的優勢。但是，由于X射線脈沖星導航不易被人為干擾，可在近地空間作為航天器自主導航的備份手段。

2005年，Woodfork提出可利用X射線脈沖星導航為GPS衛星進行軌道確定，提供了提高GPS衛星自主生存能力的備份手段［85］。衛星星座可通過星間鏈路實現星間測距從而獲得衛星間的相對位置，要獲得各衛星的絕對位置還需要借助外部參考基準。Xiong等提出了利用X射線脈沖星和星間鏈路為整個衛星星座進行自主導航的方案［86］。針對衛星星座整體旋轉問題，Liu等提出通過星間鏈路和X射線脈沖星觀測，為導航衛星星座定向參數測定提供了新的手段［87］。

為擺脫脈沖星導航對模板輪廓的依賴，鄭世界等提出了不依賴模板的單脈沖星導航方法，并利用慧眼衛星的Crab脈沖星觀測數據驗證了該方法的有效性［6-7］。該方法僅需觀測1顆脈沖星，且不需要事先構建模板輪廓。但是，該方法需要累積數天的脈沖星觀測數據，對導航的實時性有一定的影響。Sun等在該方法的基礎上進行了改進，一定程度上減少了方法所需要的數據量［88］。

此外，還有學者研究了將脈沖星導航應用于彈道導彈的導航中。王宏力等提出將脈沖星測量信息引入到已有的慣導/星光導航系統中，以削弱由于加速度計誤差所引起的位置和速度誤差，在仿真計算中獲得了較好的結果［80］。然而，由于目前X射線探測器的質量和體積較大，導航收斂慢，在彈道導彈上的應用還存在諸多困難。未來，隨著X射線探測器研制水平的提高，脈沖星導航有望成為遠程導彈導航的有力輔助手段。

3.3 脈沖星導航在深空探測的應用

目前，執行深空探測任務的航天器主要依靠地面測控系統為其提供導航服務。然而，隨著航天器距地球的距離逐漸增加，地面測控系統的導航精度逐漸降低，且時延逐漸增大。X射線脈沖星導航作為一種可在全空間內提供導航服務的航天器自主導航方法，其導航精度幾乎不受航天器距地球距離的影響。因此，X射線脈沖星導航方法在深空探測領域具有不可替代的優勢。對于深空探測器，特別是處于巡航段的深空探測器而言，其運行軌道近似于直線，這就對導航系統的可觀性提出了較高要求。因此，許多在近地空間中適用的如單X射線脈沖星導航等方法在深空探測中可能不再適用。

2008年，Graven等分析了X射線脈沖星導航在日地平動點以及深空探測軌道中的應用前景，并與美國的深空探測網進行了比較，分析表明脈沖星導航在距地球10AU以外的空間內比深空探測網更具優勢［89-90］。此外，眾多學者針對X射線脈沖星導航在水星、火星以及木星探測任務中的應用前景進行了廣泛的分析［55，64，75，91］。如圖10所示，地月空間DRO（Distant Retrograde Orbit）由于其特殊的力學特性，在地月DRO上的航天器在真實星歷和動力學環境下能夠保持數十年甚至上百年之久的對地對月有界范圍，具有極高的應用前景［92］。針對地月DRO航天器的自主導航問題，Liu等分析了利用脈沖星導航為地月空間DRO軌道航天器提供自主導航服務的可行性［93］。通過解算不同航天器接收的脈沖星信號到達時間之差，即可確定航天器在脈沖星方向上的距離，從而實現航天器 相對導航［30，37，56］。相比而言，傳統的基于視覺的相對導航方法要求航天器之間距離較近，基于激光的相對導航方法則對姿態控制的要求較高。因此，基于脈沖星的相對導航方法為深空探測器編隊飛行提供了有效且適用性廣泛的手段［56］。

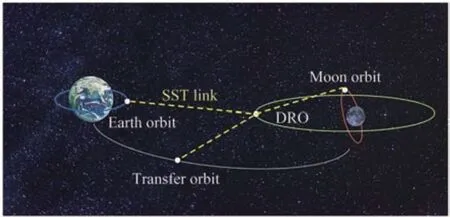
圖10 基于DRO軌道衛星的導航系統［92］Fig. 10 Concept of a DRO-based satellite navigation system［92］

為了面向未來廣泛的深空探測任務，鄭偉等提出了基于星聯網的航天器自主導航方案，星聯網中的基準航天器通過觀測X射線脈沖星實現自主導航，而后基準航天器通過星間鏈路等手段為用戶航天器提供導航服務，獲得自身位置信息的用戶航天器同時也可為其他用戶航天器提供導航服務［94］。圖11為星聯網系統的示意圖［95］。星聯網系統中的航天器均搭載相互兼容的通訊、測距設備，可通過不斷地升級擴展，隨著深空探測任務的逐漸擴展，可為更廣闊天域內的深空探測器提供導航服務。

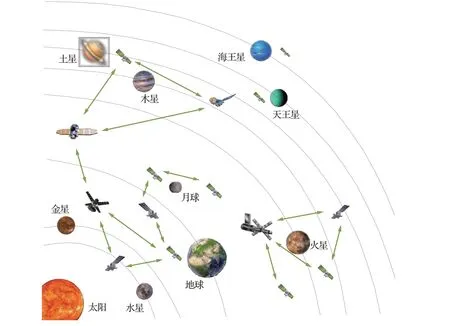
圖11 星聯網系統示意圖［95］Fig. 11 Schematic diagram of spacecraft internet［95］

4 總結與展望

經過幾十年的發展，X射線脈沖星導航技術已逐漸趨于成熟。隨著X射線脈沖星導航理論的不斷發展以及空間試驗的逐步展開，X射線脈沖星導航將逐漸走向實際工程應用，并將在深空探測、自主時間基準等領域發揮重要作用。同樣，X射線脈沖星導航技術也面臨更高的挑戰。基于工程應用中星載處理器的算力約束以及實際任務的可靠性要求，脈沖星數據處理的計算效率、導航方法的穩健性以及導航的應用模式和應用范圍方面仍需進行努力。

從面向導航的信號處理、X射線脈沖星導航理論以及X射線脈沖星導航的空間應用體制3個方面的研究進展進行了詳細的介紹。針對X射線脈沖星導航的工程應用需要，歸納了脈沖星導航技術的發展趨勢，期望為脈沖星導航的進一步研究提供參考。

1）更加高效的脈沖星數據處理方法

在脈沖星數據處理方法方面，為滿足星載計算的要求，脈沖星數據處理方法需要具備更高的計算效率。然而，現有的脈沖星數據處理方法在數據處理精度與計算時間的平衡方面仍需進一步提高。需要研究更加高效的脈沖星數據處理方法。

2）更加穩健的脈沖星導航算法

在脈沖星導航理論方面，由于空間環境的變化，航天器實際觀測得到的脈沖星信號質量是不斷變化的。此時，脈沖星數據處理所得到的脈沖TOA精度也是不斷變化的。因此，如何在空間環境不斷變化情況下，保證導航定位算法能夠穩定收斂，提供穩定可靠的導航服務，將是脈沖星導航理論的下一步發展方向。

3）更加廣泛的導航應用場景

目前，脈沖星導航應用范圍主要局限在深空飛行、星座自主運行等有限場景，有必要針對脈沖星導航的特點開拓更多的應用場景，如行星表面探測導航、大規模衛星集群自主導航、天基時空基準等。作為空間中最為穩定的頻率源，脈沖星計時觀測必將有更廣闊的應用前景。