綜合脈沖星時(shí)研究進(jìn)展

楊廷高，高玉平，3，，童明雷，李變，趙成仕，羅近濤，朱幸芝，魏飛

1．中國科學(xué)院 國家授時(shí)中心， 西安 710600 2．中國科學(xué)院 時(shí)間頻率基準(zhǔn)重點(diǎn)實(shí)驗(yàn)室， 西安 710600 3．中國科學(xué)院大學(xué) 天文與空間科學(xué)學(xué)院， 北京 100049

國 際 原 子 時(shí)（International Atomic Time，TAI）是 國 際 計(jì) 量 局（Bureau International des Poids et Mesures，BIPM）利用全世界70個(gè)守時(shí)實(shí)驗(yàn)室約460臺原子鐘和若干頻率基準(zhǔn)鐘構(gòu)建與保持的時(shí)間尺度。協(xié)調(diào)世界時(shí)（Coordinated Universal Time，UTC）與地球自轉(zhuǎn)相位相近似，與TAI只差整數(shù)秒。為進(jìn)一步修正TAI的誤差，BIPM每年還對守時(shí)與時(shí)間比對資料進(jìn)行事后處理，得到地球時(shí)TT（BIPMXXXX），其中XXXX表示發(fā)表年份［1-2］。TT（BIPMXXXX）滯后一年才能得到，一般情況下，每年更新一次。為方便起見，如不特別說明，本文也用TT表示TT（BIPMXXXX）。

原子時(shí)是積分時(shí)間尺度，具有誤差累積的特性，影響其長期頻率穩(wěn)定性。基于毫秒脈沖星自轉(zhuǎn)建立的時(shí)間尺度稱為脈沖星時(shí)。射電脈沖星計(jì)時(shí)觀測得到脈沖星脈沖到達(dá)時(shí)間（Time of Arrival，TOA）。脈沖到達(dá)時(shí)間測量是以觀測站原子鐘為參考的，通過時(shí)間比對，可將觀測站原子鐘改正到TAI或TT時(shí)間系統(tǒng)。脈沖星TOA測量等效于脈沖星鐘與參考原子鐘之間的時(shí)間比對。但因?yàn)槊}沖星與地面射電望遠(yuǎn)鏡存在復(fù)雜的相對運(yùn)動，且脈沖星的空間位置坐標(biāo)與速度、自轉(zhuǎn)參數(shù)等是未知的，所以通過TOA測量并不能立刻得到脈沖星鐘與原子鐘的鐘差。只有通過脈沖星TOA數(shù)據(jù)序列分析，測量得到脈沖星的位置、速度與自轉(zhuǎn)參數(shù)，并改正脈沖星與望遠(yuǎn)鏡之間的相對運(yùn)動影響、星際介質(zhì)傳遞的信號延遲以及相對論效應(yīng)等，才能由TOA計(jì)算得到計(jì)時(shí)殘差。理論上，如果所有物理因素（計(jì)時(shí)參考的原子時(shí)誤差除外）對TOA影響都消除掉情況下，計(jì)時(shí)殘差可看作脈沖星鐘與原子鐘比對的鐘差時(shí)間序列，將此稱為脈沖星時(shí)。可見，脈沖星時(shí)研究與影響TOA的物理因素建模和分析方法是密切相關(guān)的。與原子鐘不同，各個(gè)脈沖星鐘的頻率穩(wěn)定性、噪聲水平、TOA測量精度（取決于信號強(qiáng)弱與脈沖形狀）等是不同的，即便是毫秒脈沖星，不同脈沖星鐘性能也會有明顯差異。選擇自轉(zhuǎn)頻率穩(wěn)定的多顆毫秒脈沖星，采用合適算法構(gòu)建綜合時(shí)間尺度，可以進(jìn)一步消除單星計(jì)時(shí)噪聲以及其他誤差影響，以期得到比任何單星都更穩(wěn)定的時(shí)間尺度，即綜合脈沖星時(shí)。綜合脈沖星時(shí)建立實(shí)際上是更復(fù)雜的多顆星計(jì)時(shí)資料的綜合分析過程［3］。通常以國際原子時(shí)TAI為參考建立綜合脈沖星時(shí)（Ensemble Pulsar Time-scale，EPT），得到EPT-TAI時(shí)間序列；同樣地，如果計(jì)時(shí)觀測以TT為參考，則可以建立綜合脈沖星時(shí)EPT-TT。

射電天線配置脈沖星計(jì)時(shí)終端系統(tǒng)就可以實(shí)現(xiàn)射電脈沖星計(jì)時(shí)觀測。對選定的一組毫秒脈沖星，按照事先設(shè)計(jì)好的觀測方案，進(jìn)行長期計(jì)時(shí)觀測的工作模式，被稱為脈沖星計(jì)時(shí)陣（Pul?sar Timing Array，PTA）［4-5］。世界上著名的有北美引力波天文臺脈沖星計(jì)時(shí)陣、澳大利亞Parkes脈沖星計(jì)時(shí)陣、以及歐洲5個(gè)射電望遠(yuǎn)鏡聯(lián)合組成的脈沖星計(jì)時(shí)陣。世界上的脈沖星計(jì)時(shí)陣聯(lián)合起來，被稱為國際脈沖星計(jì)時(shí)陣（International Pulsar Timing Array，IPTA）［6-8］。至今，IPTA已經(jīng)長期堅(jiān)持60多顆毫秒脈沖星計(jì)時(shí)觀測，其中部分毫秒脈沖星已積累20年以上的資料。2016年IPTA公開釋放了49顆星的數(shù)據(jù)［9］。2019年又第二次公開釋放了65顆毫秒脈沖星數(shù)據(jù)，其中包括第一次釋放后的新觀測數(shù)據(jù)［10］。在中國，中國科學(xué)院國家天文臺、上海天文臺、新疆天文臺、云南天文臺與國家授時(shí)中心負(fù)責(zé)或參與合作觀測的5個(gè)中小口徑射電望遠(yuǎn)鏡的脈沖星計(jì)時(shí)觀測，也已經(jīng)積累了多年的計(jì)時(shí)觀測資料。近年來，中國500 m口徑射電望遠(yuǎn)鏡（Five hundred meters Aperture Spherical Radio Telescope， FAST）已經(jīng)投入毫秒脈沖星計(jì)時(shí)陣觀測項(xiàng)目，其計(jì)時(shí)觀測精度比IPTA有顯著提高。

國際上，利用IPTA資料，已經(jīng)發(fā)表了綜合脈沖星時(shí)的研究結(jié)果。中國學(xué)者采用不同算法也取得了類似的結(jié)果。射電脈沖星計(jì)時(shí)觀測原始數(shù)據(jù)經(jīng)過處理，才能得到以原子時(shí)為參考的TOA［11-12］。脈沖星計(jì)時(shí)觀測得到的TOA序列可表示為計(jì)時(shí)模型信號、計(jì)時(shí)噪聲（包括白噪聲與紅噪聲）和有關(guān)系統(tǒng)誤差的疊加［13］。用向量d表示脈沖星TOA序列數(shù)據(jù)，向量τTM表示計(jì)時(shí)模型信號，τWN表示白噪聲，τRN表示脈沖星自轉(zhuǎn)紅噪聲，τDM表示星際介質(zhì)色散延遲，τCLK表示參考原子時(shí)誤差，τEPH表示太陽系天體歷表誤差，τGW表示引力波信號，有

其中計(jì)時(shí)模型信號通過脈沖星星歷參數(shù)擬合確定（見第1節(jié)），各個(gè)脈沖星的白噪聲與紅噪聲參數(shù)采用專門設(shè)計(jì)的研究方法確定（見2.1.1節(jié)）。

星際介質(zhì)色散延遲與色散量參數(shù)（Disper?sion Measure，DM）（描述脈沖星至觀測站電子柱密度的參數(shù)）及其隨時(shí)間的變化有關(guān)。DM及其變化由多個(gè)觀測波段的TOA數(shù)據(jù)分析研究確定［14-15］。這些物理量對不同脈沖星而言，是彼此獨(dú)立的，被稱為各個(gè)脈沖星的獨(dú)立參數(shù)。計(jì)時(shí)觀測參考原子時(shí)誤差、太陽系天體歷表誤差和引力波信號與不同脈沖星之間具有各自不同的相關(guān)性［16］。這些參數(shù)被稱為脈沖星計(jì)時(shí)陣的公共參數(shù)，必須用脈沖星計(jì)時(shí)陣包括的多顆脈沖星的TOA序列分析研究確定。這些公共參數(shù)是需要提取的信號，公共參數(shù)探測與研究是IPTA的重大科學(xué)目標(biāo)。脈沖星各個(gè)獨(dú)立參數(shù)的測量誤差會影響公共參數(shù)的確定精度。因而，在研究公共參數(shù)時(shí)，根據(jù)具體情況設(shè)計(jì)合適的算法是非常重要的。通常的做法是，利用長序列（一般5年以上）TOA資料和TEMPO2軟件包［17］，先擬合得到每顆脈沖星的近似計(jì)時(shí)模型參數(shù)與DM參數(shù)，再用剩余的計(jì)時(shí)殘差序列，設(shè)計(jì)合適的研究方案，進(jìn)一步精密分析各個(gè)脈沖星的獨(dú)立參數(shù)與感興趣的公共參數(shù)。

由于主要目的是構(gòu)建綜合脈沖星時(shí)，也就是說，希望利用脈沖星計(jì)時(shí)陣長期計(jì)時(shí)殘差序列，提取出參考原子時(shí)的誤差信號，即綜合脈沖星時(shí)與計(jì)時(shí)觀測參考原子時(shí)差值的時(shí)間序列信號。為此，在構(gòu)建綜合脈沖星時(shí)的時(shí)候，必須精確測量每顆脈沖星的獨(dú)立參數(shù)，并盡量設(shè)法消除觀測設(shè)備變化、太陽系天體歷表誤差與引力波信號擾動的影響。利用國際脈沖星計(jì)時(shí)陣長期TOA資料研究表明，近年來新發(fā)布的太陽系天體歷表仍存在不可忽略的系統(tǒng)誤差，引力波信號基本上是屬于比原子時(shí)誤差更難測量的弱信號［13］。在脈沖星計(jì)時(shí)陣中，原子時(shí)誤差是單極性的，與所有脈沖星具有相同的相關(guān)性；太陽系天體歷表誤差是二極性信號，對于脈沖星計(jì)時(shí)陣中位于相反空間方向的2顆脈沖星而言，太陽系歷表誤差對二者計(jì)時(shí)殘差的影響大小相等、符號相反；引力波是更復(fù)雜的四極性信號，其對計(jì)時(shí)殘差的影響是計(jì)時(shí)陣中兩兩脈沖星對相對于觀測站張角的函數(shù)。以上3種公共參數(shù)具有各自可識別的特征［13］。設(shè)計(jì)合適的綜合脈沖星時(shí)算法，完全能夠有效提取出原子時(shí)誤差信號，并盡量消除太陽系天體歷表誤差與引力波擾動的影響。

構(gòu)建綜合脈沖星時(shí)還需要盡量消除計(jì)時(shí)噪聲影響。各個(gè)脈沖星具有不同特征的紅噪聲，其主要來自于自轉(zhuǎn)的不穩(wěn)定性，也與沒有消除掉的DM變化有關(guān)。多數(shù)毫秒脈沖星由于自轉(zhuǎn)不穩(wěn)定引起的紅噪聲是弱紅噪聲。DM隨時(shí)間變化的不確定性與星際介質(zhì)的散射效應(yīng)是射電計(jì)時(shí)觀測的主要誤差源［18-19］。DM變化的精確測量需要同時(shí)進(jìn)行多個(gè)不同波段的TOA觀測。由于DM引起的信號延遲與觀測頻率的平方成反比，因而DM不確定性對低頻觀測影響最大。鑒于此，低于1000 MHz頻率的計(jì)時(shí)觀測主要用于DM測量，但對于脈沖星時(shí)研究難以做出重要貢獻(xiàn)［20］。有的計(jì)時(shí)資料，由于沒有充分的多波段觀測數(shù)據(jù)，DM誤差會與計(jì)時(shí)紅噪聲混淆，無法將二者區(qū)分開。

觀測數(shù)據(jù)預(yù)處理是脈沖星時(shí)研究分析的必要步驟，其中包括每顆脈沖星計(jì)時(shí)模型參數(shù)初步擬合、DM及其變化影響的消除、TOA測量誤差的校準(zhǔn)和計(jì)時(shí)紅噪聲模型參數(shù)近似估計(jì)等。觀測數(shù)據(jù)預(yù)處理后得到的每顆脈沖星的計(jì)時(shí)殘差基本消去了DM與觀測系統(tǒng)變化等因素的影響，但包括有每顆星的計(jì)時(shí)噪聲與計(jì)時(shí)陣的共同信號［10］。精確的預(yù)處理，有時(shí)可以在某種程度上簡化綜合脈沖星時(shí)算法。目前，綜合脈沖星時(shí)算法有基于TEMPO2軟件的廣義最小二乘擬合、基于TEMPO2與TEMPONEST軟件的貝葉斯分析方法和維納濾波算法。

本文第1節(jié)將概述脈沖星計(jì)時(shí)模型參數(shù)擬合原理。第2節(jié)重點(diǎn)描述綜合脈沖星時(shí)的3種算法。在第3節(jié)給出綜合脈沖星時(shí)的主要研究結(jié)果與比較。第4節(jié)是有關(guān)綜合脈沖星時(shí)研究的總結(jié)與討論。

1 脈沖星計(jì)時(shí)模型參數(shù)擬合原理

脈沖星自轉(zhuǎn)頻率及其對時(shí)間的導(dǎo)數(shù)稱為脈沖星自轉(zhuǎn)參數(shù)；脈沖星的赤經(jīng)、赤緯、自行與視差，對于雙星系統(tǒng)還包括雙星軌道參數(shù)等稱為脈沖星天體測量參數(shù)，這些參數(shù)又統(tǒng)稱為計(jì)時(shí)模型參數(shù)或脈沖星星歷參數(shù)。觀測到的TOA與脈沖星脈沖輻射時(shí)刻之間的轉(zhuǎn)換關(guān)系用計(jì)時(shí)模型描述［21-22］。由于恒星際介質(zhì)與太陽系行星際介質(zhì)的色散效應(yīng)，還需要利用測得的DM參數(shù)對不同頻率觀測的TOA進(jìn)行色散延遲修正［14-15］。利用射電計(jì)時(shí)觀測資料擬合脈沖星計(jì)時(shí)模型參數(shù)，必須精確知道射電望遠(yuǎn)鏡相對于地球質(zhì)心的三維坐標(biāo)，同時(shí)，還需要知道觀測時(shí)刻地心相對于太陽系質(zhì)心的位置坐標(biāo)與速度（由已知的太陽系天體歷表提供）。

在脈沖星參考架，脈沖星脈沖發(fā)射時(shí)刻tp與其自轉(zhuǎn)參數(shù)關(guān)系可表示為

式中：t0是參考?xì)v元；t和t0是脈沖星時(shí)；φ0、v和v?分別是t0時(shí)刻脈沖星的自轉(zhuǎn)相位、頻率及其一階導(dǎo)數(shù)。假設(shè)tobs是以原子鐘為參考，地面射電望遠(yuǎn)鏡觀測得到的脈沖星脈沖TOA，tobs與tp之間有下述關(guān)系：

其中：ΔtC包括計(jì)時(shí)觀測站原子鐘到國際原子時(shí)的改正和國際原子時(shí)到質(zhì)心坐標(biāo)時(shí)（Time of Barycentric Coodinates， TCB）的改正［23-25］，這2項(xiàng)改正通常采用事先計(jì)算好的數(shù)值表內(nèi)插得到；c是光速；n是脈沖星在（太陽系）質(zhì)心坐標(biāo)系的單位矢量；V是脈沖星相對于太陽系質(zhì)心速度矢量；Δt=t?t0，即觀測時(shí)刻與參考?xì)v元差值；s是觀測時(shí)刻望遠(yuǎn)鏡相對于太陽系質(zhì)心的位置矢量；DM是色散量；vg是計(jì)時(shí)觀測頻率；k是色散常數(shù)，k=2.41×10?16Hz?2·cm?3·pc·s?1（pc為秒差距Par?sec縮寫）；R0是參考?xì)v元脈沖星相對于太陽系質(zhì)心距離；G是牛頓引力常數(shù)；Mj是第j個(gè)太陽系天體的質(zhì)量；sj是在觀測時(shí)刻望遠(yuǎn)鏡相對于第j個(gè)太陽系天體位置矢量；sj是sj是的模；n是計(jì)算Shap?iro延遲采用的太陽系主要天體數(shù)量；sΘ是觀測時(shí)刻望遠(yuǎn)鏡到太陽的距離；mΘ是太陽質(zhì)量；Ψ是太陽和脈沖星在觀測時(shí)刻相對望遠(yuǎn)鏡的張角。

式（3）中，tobs（觀測得到的TOA）和s（望遠(yuǎn)鏡相對于太陽系質(zhì)心矢量）為已知量，其中s由望遠(yuǎn)鏡相對地心位置矢量（事先已知），利用地球自轉(zhuǎn)參數(shù)、歲差、章動和太陽系天體歷表提供的地心相對于太陽系質(zhì)心位置坐標(biāo)計(jì)算得到［21］。式（3）右邊第3項(xiàng)是由于望遠(yuǎn)鏡相對脈沖星運(yùn)動引起的脈沖信號延遲改正，稱作Roemer延遲，第4項(xiàng)是視差改正項(xiàng)，第5項(xiàng)是與脈沖星速度有關(guān)的一階多普勒改正，第6項(xiàng)是與觀測頻率有關(guān)的色散延遲改正，第7項(xiàng)是脈沖星加速度引起的改正，第8項(xiàng)與第9項(xiàng)是Shapiro延遲改正，式（3）最后一項(xiàng)Δtob是脈沖雙星軌道運(yùn)動延遲改正，包括軌道運(yùn)動的Roemer延遲、Shapiro延遲和時(shí)間坐標(biāo)相對論改正等［21］。

脈沖信號的真空傳播延遲包括由于相對運(yùn)動引起的隨時(shí)間變化分量和不變的常數(shù)分量。式（3）只計(jì)算延遲隨時(shí)間變化的分量，忽略常數(shù)分量，雖然常數(shù)分量是個(gè)很大的數(shù)值。另外，式（3）還應(yīng)該包括觀測系統(tǒng)（設(shè)備）變化引起的TOA跳變。脈沖星在參考?xì)v元t0的自轉(zhuǎn)相位φ0、自轉(zhuǎn)頻率v及其導(dǎo)數(shù)v?是待求的自轉(zhuǎn)參數(shù)。對于毫秒脈沖星，自轉(zhuǎn)頻率的二階導(dǎo)數(shù)可以忽略，但對于自轉(zhuǎn)較慢的普通脈沖星，自轉(zhuǎn)參數(shù)還應(yīng)該包括自轉(zhuǎn)頻率的二階及其以上高階導(dǎo)數(shù)。式（3）中脈沖星位置矢量（包括方向和距離）以及運(yùn)動速度參數(shù)與通常采用的脈沖星赤經(jīng)、赤緯、自行與視差參數(shù)之間具有確定的轉(zhuǎn)換關(guān)系，這些是待求的天體測量參數(shù)［26-27］。脈沖星計(jì)時(shí)觀測只能測量自行，不能測量視向速度。對于脈沖雙星，待求的參數(shù)還應(yīng)該包括脈沖星的軌道參數(shù)以及可能測量的后開普勒參數(shù)［28-31］。

通常脈沖星計(jì)時(shí)模型參數(shù)的近似值總是知道的，對于小量參數(shù)，如脈沖星自轉(zhuǎn)頻率的導(dǎo)數(shù)等，其近似值可設(shè)為0。將參數(shù)近似值作為采用值分別代入式（2）和式（3），利用脈沖星的長期計(jì)時(shí)觀測得到的TOA時(shí)間序列（n個(gè)TOA），可以計(jì)算得到每個(gè)TOA的計(jì)時(shí)殘差。在忽略脈沖星紅噪聲情況下，計(jì)時(shí)殘差的系統(tǒng)性變化被認(rèn)為是由脈沖星參數(shù)采用值誤差所致。利用脈沖星計(jì)時(shí)殘差（稱為擬合前殘差）采用最小二乘擬合，可以進(jìn)一步得到脈沖星參數(shù)采用值的改正值及其協(xié)方差。最小二乘擬合需要將非線性方程式（3）在各個(gè)參數(shù)采用值處進(jìn)行級數(shù)展開，從而把式（3）轉(zhuǎn)換成包含脈沖星參數(shù)采用值誤差的線性方程。假設(shè)R向量是擬合前的計(jì)時(shí)殘差，脈沖星參數(shù)采用值的誤差向量為P，脈沖星參數(shù)的系數(shù)矩陣（也稱為計(jì)時(shí)模型矩陣）為M，如果觀測TOA數(shù)量為n，脈沖星參數(shù)總數(shù)量為m（n>m），則M是n×m的矩陣。用矩陣表示的最小二乘擬合的線性方程為

式中：E是擬合后的計(jì)時(shí)殘差向量。參數(shù)的最小二乘解為

通過迭代，利用式（4）可以得到更精確的脈沖星參數(shù)解及其協(xié)方差。實(shí)際上，考慮到各個(gè)TOA測量誤差不同，需要利用式（4）采用加權(quán)最小二乘求解，權(quán)取為1σ2i，σi是第i個(gè)TOA的誤差，稱為白噪聲（與觀測時(shí)間無關(guān)的噪聲）。另外，考慮到脈沖星紅噪聲（與觀測時(shí)間相關(guān)的隨機(jī)噪聲）影響，脈沖星計(jì)時(shí)模型參數(shù)擬合往往采用更復(fù)雜的算法（見2.1節(jié)）。TEMPO2軟件及其插件是國際上進(jìn)行脈沖星計(jì)時(shí)分析的基礎(chǔ)性軟件系統(tǒng)。

2 綜合脈沖星時(shí)算法概述

綜合脈沖星時(shí)算法的基礎(chǔ)是正確擬合脈沖星計(jì)時(shí)模型參數(shù)，以便得到每顆星的計(jì)時(shí)殘差。構(gòu)建綜合脈沖星時(shí)，就是從多顆脈沖星計(jì)時(shí)殘差提取參考原子時(shí)誤差信息的過程。在毫秒脈沖星計(jì)時(shí)觀測初期，學(xué)者采用加權(quán)平均方法計(jì)算綜合脈沖星時(shí)。將計(jì)時(shí)殘差近似看作包含計(jì)時(shí)噪聲和綜合脈沖星時(shí)信號的時(shí)間序列。通過多顆脈沖星計(jì)時(shí)殘差加權(quán)平均，進(jìn)一步消除脈沖星計(jì)時(shí)噪聲，從而得到綜合脈沖星時(shí)［32］。隨著脈沖星數(shù)量增加與計(jì)時(shí)觀測精度提高，綜合脈沖星時(shí)算法逐步趨于改進(jìn)、優(yōu)化與完善。

2.1 基于TEMPO2軟件的廣義最小二乘擬合算法

2.1.1 脈沖星計(jì)時(shí)模型參數(shù)的廣義最小二乘擬合

脈沖星計(jì)時(shí)觀測在一定積分時(shí)間內(nèi)得到積分脈沖輪廓。利用相同波段大量觀測平均建立模板脈沖輪廓。積分脈沖輪廓與模板脈沖輪廓擬合得到TOA，同時(shí)也提供TOA的擬合誤差［12］。實(shí)際上，觀測得到的TOA的不確定性比其擬合誤差要復(fù)雜得多，TOA擬合誤差往往不能反映TOA觀測的真實(shí)誤差。首先，由于星際閃爍效應(yīng)，實(shí)際觀測得到的脈沖強(qiáng)度隨時(shí)間迅速變化，從而導(dǎo)致在不同時(shí)刻的觀測信噪比是不同的［33］。另外，脈沖星輻射的脈沖形狀具有抖動（Jitter）現(xiàn)象，TOA的不確定性還應(yīng)該包括脈沖形狀抖動引起的誤差。假設(shè)第i個(gè)TOA的脈沖輪廓擬合誤差為>σi，為其估計(jì)的真誤差，二者具有下述關(guān)系：

式中：EFAC是比例因子；EQUAD是代表脈沖抖動的參數(shù)。這2個(gè)參數(shù)可以針對脈沖星每個(gè)觀測系統(tǒng)數(shù)據(jù)，應(yīng)用TEMPO2插件EFACEQUAD分析確定［20］。利用可以構(gòu)建白噪聲協(xié)方差矩陣（對角線元素是每個(gè)TOA的方差，矩陣的其余元素為0）。

用脈沖星長期計(jì)時(shí)資料擬合脈沖星模型參數(shù)還應(yīng)該考慮到紅噪聲與DM變化影響。假定DM變化影響已經(jīng)消除，只討論紅噪聲存在情況下脈沖星參數(shù)擬合問題［34］。紅噪聲只取決于脈沖星，與觀測頻率無關(guān)。利用式（4）得到擬合后計(jì)時(shí)殘差，除去白噪聲以外，擬合后計(jì)時(shí)殘差還包含有與時(shí)間相關(guān)的紅噪聲。用冪律模型描述擬合后計(jì)時(shí)殘差功率譜密度［35-36］：

式中：P0是功率譜幅度；γ是譜指數(shù)；f是傅里葉頻率；fc是紅譜與白譜交叉點(diǎn)（拐點(diǎn)）的傅里葉頻率。

利用TEMPO2的SPECTRALMODEL插件，由計(jì)時(shí)殘差分析確定式（7）的參數(shù)，從而得到理論功率譜。再對理論功率譜進(jìn)行傅里葉變換，可以得到反映紅噪聲影響的計(jì)時(shí)殘差的協(xié)方差函數(shù)，進(jìn)而構(gòu)建紅噪聲協(xié)方差矩陣。將紅噪聲與白噪聲協(xié)方差矩陣之和表示為C，則脈沖星計(jì)時(shí)模型參數(shù)的廣義最小二乘解可表示為

對C進(jìn)行Cholesky分解，得到矩陣U，C=UUT。用矩陣U?1分別對R和M進(jìn)行歸一化和白化，即定義RW=U?1R，MW=U?1M，則脈沖星計(jì)時(shí)模型參數(shù)的廣義最小二乘解也可表示為

式（9）與普通最小二乘解表達(dá)式（5）具有相同的形式，其解與式（8）結(jié)果相同。為方便起見，TEMPO2應(yīng)用式（9）求解。如果脈沖星紅噪聲的功率譜計(jì)算是正確的，用Cholesky分解計(jì)算得到的RW的功率譜應(yīng)該是白譜，則式（9）結(jié)果是正確的。否則，需要迭代運(yùn)算，以便求得精確的脈沖星參數(shù)解。經(jīng)驗(yàn)表明，在大多數(shù)情況下，迭代過程收斂很快，往往只需一次或二次迭代就能獲得正確結(jié)果。與普通最小二乘方法相比，廣義最小二乘解析表達(dá)式包括了與計(jì)時(shí)噪聲相關(guān)的協(xié)方差矩陣，能夠有效避免計(jì)時(shí)噪聲對計(jì)時(shí)模型參數(shù)擬合的影響，從而得到更精確的脈沖星參數(shù)及其協(xié)方差［36］。由于該方法必須對每顆星進(jìn)行譜分析，該算法又稱為頻率分析方法。

為擬合并消除DM變化影響，一般情況下，還需要利用多個(gè)波段的TOA序列數(shù)據(jù)，在采用廣義最小二乘擬合脈沖星計(jì)時(shí)模型參數(shù)時(shí)，再增加DM隨時(shí)間變化的參數(shù)。在考慮到計(jì)時(shí)噪聲情況下，同時(shí)擬合得到脈沖星計(jì)時(shí)模型參數(shù)與DM變化參數(shù)［15］。DM變化參數(shù)模型采用等時(shí)間間隔采樣的線性模型，并增加約束條件，使得所有采樣點(diǎn)DM變化值的和等于0。在測量DM變化時(shí)，必須計(jì)及紅噪聲對DM測量的影響。有關(guān)DM變化測量的詳細(xì)描述，請參考文獻(xiàn)［15］。

以上描述的單顆脈沖星計(jì)時(shí)模型參數(shù)求解方法可以推廣到多顆脈沖星同時(shí)求解的情況，目的是分析研究多顆脈沖星的公共參數(shù)，如參考鐘誤差等。首先需要將每顆星的計(jì)時(shí)殘差按照脈沖星編號順序組合在一起，形成包含所有脈沖星的計(jì)時(shí)殘差向量。將待擬合的公共參數(shù)與每顆脈沖星的獨(dú)立參數(shù)依次組合成總參數(shù)向量，利用每顆脈沖星參數(shù)的采用值與公共參數(shù)數(shù)學(xué)模型計(jì)算得到總參數(shù)的系數(shù)矩陣。在計(jì)及每顆脈沖星白噪聲與紅噪聲情況下，采用廣義最小二乘同時(shí)擬合每顆脈沖星計(jì)時(shí)模型參數(shù)與公共參數(shù)。為簡化計(jì)時(shí)殘差協(xié)方差矩陣計(jì)算，每顆脈沖星的白噪聲與紅噪聲參數(shù)可采用單星計(jì)時(shí)分析的結(jié)果，在此基礎(chǔ)上構(gòu)建初步的總計(jì)時(shí)殘差的協(xié)方差矩陣。然后應(yīng)用廣義最小二乘迭代求解。

2.1.2 包括脈沖星鐘誤差參數(shù)的廣義最小二乘擬合算法

脈沖星計(jì)時(shí)觀測參考的原子時(shí)系統(tǒng)誤差就是要提取的綜合脈沖星時(shí)信號，簡稱為鐘誤差信號。鐘誤差是脈沖星計(jì)時(shí)陣中所有脈沖星計(jì)時(shí)殘差中都包含的共同信號。只要建立能夠描述鐘誤差信號的數(shù)學(xué)模型，在每顆脈沖星獨(dú)立參數(shù)（計(jì)時(shí)模型參數(shù)）的基礎(chǔ)上，進(jìn)一步增加鐘誤差公共參數(shù)，就能夠利用脈沖星計(jì)時(shí)陣多顆脈沖星的長期觀測資料，采用廣義最小二乘擬合算法，同時(shí)擬合得到每顆脈沖星的獨(dú)立參數(shù)與綜合脈沖星時(shí)參數(shù)。描述綜合脈沖星時(shí)最簡單的數(shù)學(xué)模型就是對其信號按照時(shí)間進(jìn)行等間距采樣。因要提取的信號是低頻信號，其采樣間隔可根據(jù)觀測TOA采樣平均間隔設(shè)計(jì)為半年或90 d等。因鐘誤差隨時(shí)間呈現(xiàn)緩慢變化趨勢，在其信號的每個(gè)采樣間隔內(nèi)，再采用線性內(nèi)插法提取每個(gè)采樣點(diǎn)的信號［3，15，20］。

對于包括脈沖星鐘誤差參數(shù)在內(nèi)的多顆星計(jì)時(shí)分析的廣義最小二乘算法，組合得到的包含所有脈沖星的總計(jì)時(shí)殘差向量為Rtot（假定Rtot已經(jīng)消除了每顆脈沖星DM變化的影響），包括鐘誤差模型參數(shù)與每顆脈沖星計(jì)時(shí)模型參數(shù)（參數(shù)采用值的改正值）的總參數(shù)向量為Ptot，待擬合的所有參數(shù)的總系數(shù)矩陣為Mtot。于是，可得如下線性方程：

式中：Etot是擬合后總計(jì)時(shí)殘差向量。

應(yīng)該指出的是需要擬合的綜合脈沖星時(shí)參數(shù)與脈沖星某些計(jì)時(shí)模型參數(shù)具有相關(guān)性。從式（2）和式（3）可以看出，鐘誤差隨時(shí)間的變化與脈沖星自轉(zhuǎn)頻率及其一階導(dǎo)數(shù)相關(guān)，鐘誤差的周年變化與脈沖星的位置、自行參數(shù)相關(guān)。為盡量減小這種相關(guān)性影響，需要在最小二乘方程式（10）的基礎(chǔ)上再增加以下約束條件方程［15，37］：

式中：ΔC(ti)是綜合脈沖星時(shí)信號在ti（i=1，2，…，n）時(shí)刻的采樣值；?=2π年。加入這些約束條件，將綜合脈沖星時(shí)信號與計(jì)時(shí)模型參數(shù)（主要是自轉(zhuǎn)參數(shù)與脈沖星位置參數(shù)）的協(xié)方差減到最小。這些約束條件方程式連同式（10）共同構(gòu)成如下最小二乘方程式：

其中：B是描述約束條件的矩陣；RB是約束條件向量，根據(jù)式（11）～式（15），有RB=0；EB向量是約束條件方程的擬合后殘差。式（16）是利用多顆脈沖星同時(shí)擬合綜合脈沖星時(shí)信號與每顆脈沖星各自計(jì)時(shí)模型參數(shù)的基本最小二乘方程。考慮到脈沖星計(jì)時(shí)觀測不可忽略的白噪聲與紅噪聲，還需要計(jì)算總計(jì)時(shí)殘差的協(xié)方差矩陣（包括白噪聲與紅噪聲的協(xié)方差矩陣），并采用廣義最小二乘法同時(shí)擬合得到綜合脈沖星時(shí)與每顆脈沖星的計(jì)時(shí)模型參數(shù)（見2.1.1節(jié)）。

隨著脈沖星數(shù)量增加，計(jì)時(shí)殘差向量長度大大增加，待擬合的參數(shù)也更多。在這種情況下，為簡化廣義最小二乘擬合過程，最好應(yīng)用廣義最小二乘法，首先單獨(dú)分析得到每顆脈沖星的計(jì)時(shí)噪聲參數(shù)與計(jì)時(shí)模型參數(shù)。然后，將每顆星的噪聲參數(shù)用作計(jì)算多顆星總協(xié)方差矩陣的采用值，將每顆脈沖星的天體測量參數(shù)作為已知量，于是，式（16）中待擬合的參數(shù)向量Ptot只包含綜合脈沖星時(shí)參數(shù)與每顆星的自轉(zhuǎn)參數(shù)［20］。由于待擬合參數(shù)相對減少，擬合過程更易操作，也能夠保障取得可靠的綜合脈沖星時(shí)結(jié)果，但一至二次迭代過程是必要的。

在廣義最小二乘擬合算法中，因引力波、太陽系行星歷表誤差對計(jì)時(shí)殘差影響具有與綜合脈沖星時(shí)不同的特征，在很大程度上能夠削弱二者對綜合脈沖星時(shí)信號的影響。

脈沖星TOA的非均勻采樣、各個(gè)脈沖星觀測總時(shí)間跨度不同，再加上綜合脈沖星時(shí)參數(shù)的線性內(nèi)插，會導(dǎo)致其信號的各個(gè)采樣點(diǎn)之間具有不同程度的相關(guān)性［3，20］。在廣義最小二乘算法輸出的總參數(shù)向量的協(xié)方差矩陣中，綜合脈沖星時(shí)各個(gè)采樣點(diǎn)之間的協(xié)方差能夠反映這種相關(guān)性。各采樣點(diǎn)方差的平方根是綜合脈沖星時(shí)數(shù)值本身的1σ誤差。

2.2 綜合脈沖星時(shí)貝葉斯算法

綜合脈沖星時(shí)的貝葉斯算法，是在脈沖星計(jì)時(shí)分析貝葉斯方法的基礎(chǔ)上發(fā)展起來的一種算法。脈沖星計(jì)時(shí)分析貝葉斯方法基于貝葉斯推論，能夠同時(shí)估計(jì)脈沖星計(jì)時(shí)模型參數(shù)與計(jì)時(shí)噪聲模型參數(shù)［38-42］，其基本分析軟件為TEMPONEST［40］。

2.2.1 貝葉斯推論原理

貝葉斯推論表示為

式中：Pr(Θ|D，H)≡Pr(Θ)是給定觀測數(shù)據(jù)D和物理模型H情況下，模型參數(shù)Θ的后驗(yàn)概率分布密度；Pr(D|Θ，H)≡L(Θ)是似然函數(shù)，即，給定物理模型及其參數(shù)情況下，觀測數(shù)據(jù)的概率分布密度；Pr(Θ|H)≡π(Θ)是給定物理模型情況下，模型參數(shù)的先驗(yàn)概率分布密度；Pr(D|H)≡Z是貝葉斯證據(jù)。貝葉斯證據(jù)與參數(shù)Θ無關(guān)，因此，用式（17）估計(jì)模型參數(shù)時(shí)，可以忽略貝葉斯證據(jù)項(xiàng)（即假設(shè)其值是1）。

為估計(jì)模型參數(shù)Θ，需要采用合適方法從參數(shù)的后驗(yàn)概率分布對參數(shù)進(jìn)行采樣，例如采用標(biāo)準(zhǔn)馬爾科夫鏈蒙特卡洛（Markov Chain Monte Carlo，MCMC）采樣方法，再從參數(shù)Θ的大量采樣樣本統(tǒng)計(jì)得到參數(shù)估計(jì)值及其誤差。為計(jì)算參數(shù)Θ的后驗(yàn)概率分布，其先驗(yàn)概率分布是必須知道的，一般可假定為均勻分布。貝葉斯證據(jù)對模型選擇起決定作用。例如，對于同一觀測數(shù)據(jù)D，為比較2個(gè)模型的優(yōu)劣，需要分別計(jì)算這2個(gè)模型的貝葉斯證據(jù)Z，通常Z值較大的模型更優(yōu)越。如果兩模型的Z值接近，則優(yōu)先采用參數(shù)較少、相對簡單的模型。貝葉斯證據(jù)計(jì)算公式為

式中：n是參數(shù)空間的維數(shù)，顯然描述模型的參數(shù)越多，證據(jù)計(jì)算越繁重。國際上已經(jīng)建立的MULTINEST算法能夠有效進(jìn)行脈沖星模型參數(shù)后驗(yàn)概率分布采樣，也能同時(shí)計(jì)算并給出貝葉斯證據(jù)［40，42］。

2.2.2 脈沖星計(jì)時(shí)似然函數(shù)

應(yīng)用貝葉斯方法進(jìn)行脈沖星計(jì)時(shí)分析，首先需要寫出貝葉斯公式式（17）中的似然函數(shù)表達(dá)式。下面按照從簡單到復(fù)雜的3種情況，分別導(dǎo)出觀測數(shù)據(jù)TOA向量d的似然函數(shù)［40］。

1）假設(shè)d=τTM(ε)+τSTO，τTM(ε)是計(jì)時(shí)模型參數(shù)向量ε的函數(shù)，代表確定性的計(jì)時(shí)模型信號。τSTO是服從高斯過程的隨機(jī)分量，對于第i個(gè)TOA，其不確定性σi代表隨機(jī)分量。假設(shè)TOA數(shù)量為n，計(jì)時(shí)觀測的似然函數(shù)可寫為

式（19）是貝葉斯分析方法最簡單的只包括脈沖星計(jì)時(shí)模型參數(shù)的似然函數(shù)表達(dá)式。

2）為正確描述脈沖星TOA白噪聲，和2.1.1節(jié)的討論一樣，需要引入σi的2個(gè)修正因子EFAC與EQUAD。修正σi后的白噪聲為

式中：α和β分別代表EFAC和EQUAD參數(shù)。注意式（20）與式（6）是不相同的，包括脈沖星計(jì)時(shí)模型參數(shù)與白噪聲參數(shù)的似然函數(shù)表達(dá)式為

3）下面討論再進(jìn)一步包括脈沖星計(jì)時(shí)紅噪聲的情況。用冪律模型表示脈沖星紅噪聲的功率譜密度［20，38，40，43］為

式中：Ared是紅噪聲的幅度；γred是譜指數(shù)，二者是紅噪聲功率譜模型參數(shù)；fc=1/年。計(jì)時(shí)觀測的協(xié)方差矩陣由紅噪聲協(xié)方差矩陣與白噪聲協(xié)方差陣構(gòu)成。紅噪聲的協(xié)方差矩陣的計(jì)算式為［20］

其中：下標(biāo)i、j表示第i、第j個(gè)計(jì)時(shí)TOA，tij是第i和第j個(gè)TOA時(shí)刻的差值。積分下限頻率為1T，T是TOA的總時(shí)間跨度。低于1T的傅里葉頻率分量，在脈沖星自轉(zhuǎn)參數(shù)擬合時(shí)被吸收到自轉(zhuǎn)參數(shù)中了。白噪聲的協(xié)方差矩陣用修正后的白噪聲構(gòu)建，是對角線矩陣N。單顆脈沖星計(jì)時(shí)觀測的總協(xié)方差矩陣為C=N+Cred，Cred為紅噪聲協(xié)方差矩陣。于是，同時(shí)包括計(jì)時(shí)模型參數(shù)、白噪聲與紅噪聲參數(shù)的計(jì)時(shí)觀測似然函數(shù)表達(dá)式為

對于單顆脈沖星計(jì)時(shí)分析，用式（24）代替貝葉斯公式（17）中的L(Θ)項(xiàng)，可以用貝葉斯方法估計(jì)得到計(jì)時(shí)模型參數(shù)、白噪聲、紅噪聲參數(shù)及其誤差。和紅噪聲一樣，DM變化的功率譜也可以用冪律模型描述。對于單顆脈沖星多個(gè)波段的觀測資料，還可以寫出再包括DM隨時(shí)間變化參數(shù)的似然函數(shù)，從而在分析脈沖星計(jì)時(shí)模型與噪聲參數(shù)的同時(shí)，也分析DM變化參數(shù)［14］。和最小二乘分析方法類似，脈沖星計(jì)時(shí)的貝葉斯分析也要求事先知道脈沖星各類參數(shù)的近似值。如果只對某類參數(shù)感興趣，可以將其他參數(shù)邊際化［38］，集中分析感興趣的少數(shù)參數(shù)。

上述單星計(jì)時(shí)分析的3個(gè)似然函數(shù)表達(dá)式式（19）、式（21）和式（24）中，計(jì)時(shí)模型參數(shù)與TOA關(guān)系都是式（3）描述的非線性關(guān)系，貝葉斯方法能夠用非線性分析方法直接求解脈沖星計(jì)時(shí)模型參數(shù)與計(jì)時(shí)噪聲參數(shù)。如果先用TEMPO2軟件對TOA序列數(shù)據(jù)（d向量）采用最小二乘方法（見本文第1節(jié)）得到初步擬合后計(jì)時(shí)殘差δtpost與計(jì)時(shí)模型參數(shù)近似估計(jì)值，然后，用δtpost?Mδε（δε是脈沖星計(jì)時(shí)模型參數(shù)近似值的改正值，M是計(jì)時(shí)模型參數(shù)的系數(shù)矩陣）代替式（19）、式（21）和式（24）中的d?τTM(ε)，則這3個(gè)似然函數(shù)表達(dá)式中，計(jì)時(shí)模型就變成線性近似的形式了。用貝葉斯方法基于線性近似計(jì)時(shí)模型的似然函數(shù)表達(dá)式，也可以正確地求解脈沖星計(jì)時(shí)模型參數(shù)與計(jì)時(shí)噪聲參數(shù)。在同時(shí)對多顆脈沖星資料進(jìn)行分析時(shí)，采用線性近似計(jì)時(shí)模型更方便。在下面討論綜合脈沖星時(shí)貝葉斯算法時(shí)，采用脈沖星計(jì)時(shí)模型線性近似的分析方法。

2.2.3 綜合脈沖星時(shí)的貝葉斯算法

原理上，貝葉斯方法可以擴(kuò)展為基于多顆脈沖星在多個(gè)頻率的長期計(jì)時(shí)觀測資料，同時(shí)分析各個(gè)脈沖星計(jì)時(shí)模型參數(shù)、計(jì)時(shí)噪聲參數(shù)、DM變化模型參數(shù)、綜合脈沖星時(shí)參數(shù)、太陽系行星歷表誤差參數(shù)與引力波參數(shù)等的綜合性分析方法。與單星分析相比，多星分析的參數(shù)數(shù)量急劇增加。不僅物理模型更復(fù)雜，且貝葉斯算法計(jì)算量更大，耗費(fèi)計(jì)算時(shí)間更多。貝葉斯方法又可細(xì)分為多種不同具體算法，包括時(shí)域分析算法和時(shí)-頻域分析算法［40-41］。不同算法的差異主要是各類噪聲信號數(shù)學(xué)描述的不同。另外，還研究發(fā)展了從多維空間后驗(yàn)概率分布密度采樣的不同方法，以便提高采樣速度與可靠性［41］。

貝葉斯方法用冪律功率譜模型描述綜合脈沖星時(shí)信號的功率譜，用最大似然估計(jì)方法估計(jì)綜合脈沖星時(shí)信號模型參數(shù)，再用估計(jì)得到的信號模型參數(shù)重構(gòu)脈沖星時(shí)信號波形。

為方便綜合脈沖星時(shí)研究，首先用TEMPO2軟件針對每顆毫秒脈沖星長期計(jì)時(shí)觀測TOA序列進(jìn)行分析，得到每顆星擬合后計(jì)時(shí)殘差δtp，post與計(jì)時(shí)模型參數(shù)的初步估計(jì)值。假設(shè)擬合后計(jì)時(shí)殘差已經(jīng)消除了DM誤差影響，所以，每顆星擬合后殘差主要包括計(jì)時(shí)噪聲與感興趣的鐘誤差信號。參考式（24），對于單顆脈沖星，擬合后計(jì)時(shí)殘差的線性計(jì)時(shí)模型形式的似然函數(shù)可表示為

式中：n是殘差數(shù)；C是計(jì)時(shí)殘差的協(xié)方差矩陣（白噪聲與紅噪聲協(xié)方差矩陣之和）；Mp是計(jì)時(shí)模型參數(shù)的系數(shù)矩陣（計(jì)時(shí)模型矩陣）；δεp是計(jì)時(shí)模型參數(shù)改正值。

為求解綜合脈沖星時(shí)信號，需要將單顆脈沖星的似然函數(shù)表達(dá)式擴(kuò)展到多顆脈沖星，并包括參考鐘誤差（綜合脈沖星時(shí)）信號的情況。將多顆脈沖星計(jì)時(shí)殘差按照脈沖星順序組合在一起，構(gòu)成總的計(jì)時(shí)殘差向量。一般情況下，多顆脈沖星計(jì)時(shí)殘差能夠近似覆蓋共同時(shí)間段。原理上，在同一時(shí)間段內(nèi)觀測的星數(shù)越多，TOA數(shù)據(jù)越密，提取的鐘信號誤差會越小，反之則誤差較大。各個(gè)脈沖星紅噪聲用式（22）冪律模型描述，彼此相互獨(dú)立。作為所有脈沖星共同信號的綜合脈沖星時(shí)功率譜也用冪律模型描述［20，43］，有

式中：Aclk（譜幅度）與γclk（譜指數(shù)）是需要用貝葉斯分析方法求解的鐘信號參數(shù)。因?yàn)楦鱾€(gè)脈沖星計(jì)時(shí)模型參數(shù)改正值是線性的，其函數(shù)形式已知，可以解析地將每顆脈沖星計(jì)時(shí)模型參數(shù)邊際化［38-39］。只包含綜合脈沖星時(shí)與各個(gè)脈沖星計(jì)時(shí)噪聲參數(shù)的多顆星總計(jì)時(shí)殘差向量δt的似然函數(shù)可表示為［20，43］

式中：δt=δtpost?M(δε)，δtpost是多顆星擬合后總計(jì)時(shí)殘差向量，δε是按順序組合在一起的多顆星的計(jì)時(shí)模型參數(shù)改正值，M是δε的系數(shù)矩陣；I、J表示第I、第J顆脈沖星，i、j是指每顆脈沖星的第i、第j個(gè)殘差；Ctot=CW+CTN+Cclk，其中Ctot是多顆脈沖星計(jì)時(shí)殘差的總協(xié)方差矩陣，CW、CTN和Cclk分別是多顆星計(jì)時(shí)殘差的白噪聲、紅噪聲和綜合脈沖星時(shí)信號的協(xié)方差矩陣。因?yàn)楦鱾€(gè)脈沖星的計(jì)時(shí)噪聲是彼此獨(dú)立的，當(dāng)I≠J時(shí)，CW，I，J=0，CTN，I，J=0。綜合脈沖星時(shí)是所有星的共 同 信 號，有Cclk，I，J，i，j=Cclk，i，jCclk，I，J，當(dāng)I≠J時(shí)，Cclk，I，J=1。式（27）中有：

因?yàn)楦信d趣的是綜合脈沖星時(shí)參數(shù)，用貝葉斯方法計(jì)算綜合脈沖星時(shí)冪律譜模型參數(shù)Aclk和γclk的后驗(yàn)概率分布時(shí)，還可以采用數(shù)值方法將式（27）中的其他噪聲模型參數(shù)邊際化［38-40］。由邊際化的后驗(yàn)分布，用合適采樣方法，得到脈沖星時(shí)冪律譜模型參數(shù)及其誤差估計(jì)。綜合脈沖星時(shí)譜模型參數(shù)確定后，就知道了與綜合脈沖星時(shí)有關(guān)的總計(jì)時(shí)殘差的協(xié)方差矩陣，進(jìn)而可以用非等間隔采樣的廣義維納濾波方法構(gòu)建綜合脈沖星時(shí)波形與協(xié)方差矩陣［20，43］。還可用廣義維納濾波內(nèi)插信號采樣數(shù)據(jù)點(diǎn)，如內(nèi)插成等間距數(shù)據(jù)點(diǎn)，或外推預(yù)報(bào)信號數(shù)據(jù)點(diǎn)［14，44］。綜合脈沖星時(shí)信號的波形及其協(xié)方差的計(jì)算式為

受計(jì)時(shí)殘差δt誤差影響，由式（29）得到的綜合脈沖星時(shí)clk包含有不可忽略的高頻噪聲，進(jìn)一步濾除高頻噪聲是必要的。

2.3 綜合脈沖星時(shí)維納濾波算法

脈沖星計(jì)時(shí)觀測TOA序列利用TEMPO2正確擬合脈沖星計(jì)時(shí)模型參數(shù)后的殘差，進(jìn)一步經(jīng)過預(yù)處理后，得到按采樣時(shí)間均勻分布的計(jì)時(shí)殘差序列，記為觀測殘差向量rI，下標(biāo)代表第I顆脈沖星。rI包含脈沖星時(shí)信號、計(jì)時(shí)噪聲與其他弱擾動信號（如太陽系行星歷表誤差、引力波）。令Qss表示與綜合脈沖星時(shí)信號有關(guān)的計(jì)時(shí)殘差的協(xié)方差矩陣，QrI表示殘差向量rI（包括信號與噪聲）的協(xié)方差矩陣，wI是第I顆脈沖星歸一化的權(quán)重。假設(shè)共n顆脈沖星，則綜合脈沖星時(shí)信號的最佳估計(jì)為［45-46］

維納濾波的關(guān)鍵是如何從多顆脈沖星各自的殘差向量rI估計(jì)QrI和Qss。首先需要估計(jì)協(xié)方差函數(shù)，然后由協(xié)方差函數(shù)構(gòu)建協(xié)方差矩陣。顯然，至少具有2顆以上脈沖星的觀測才能估計(jì)共同信號的協(xié)方差函數(shù)。對于n顆脈沖星，可組成m個(gè)相互獨(dú)立的脈沖星對，這里m=n(n?1)/2。由每個(gè)脈沖星對估計(jì)得到其脈沖星時(shí)信號（脈沖星對的共同信號）的互協(xié)方差函數(shù)。再由m個(gè)信號互協(xié)方差函數(shù)的平均得到綜合脈沖星時(shí)信號的平均互協(xié)方差函數(shù)，進(jìn)而得到Qss。由于不同脈沖星的計(jì)時(shí)噪聲是互相獨(dú)的，平均互協(xié)方差函數(shù)能夠較好地消除各個(gè)脈沖星計(jì)時(shí)噪聲的影響，也能最大程度地消除其他弱擾動信號影響。再由每顆脈沖星殘差向量rI分別估計(jì)它們各自的自協(xié)方差函數(shù)，進(jìn)而得到QrI。

脈沖星的自協(xié)方差與互協(xié)方差函數(shù)計(jì)算采用下述算法［45］。將脈沖星殘差向量rI進(jìn)一步表示為rI，L，下標(biāo)I表示第I顆脈沖星，下標(biāo)L是殘差向量的第L個(gè)數(shù)據(jù)點(diǎn)，N是向量rI，L的長度，令δ為計(jì)時(shí)殘差采樣間隔，第I顆星殘差向量的傅里葉變換為

式中：hL是殘差向量的平滑窗函數(shù)，選擇合適的平滑窗函數(shù)可以盡量減小頻譜滲漏的影響［36］。n顆脈沖星的自功率譜（I=K）和互功率譜（I≠K）的計(jì)算式為

式中：(·)*表示復(fù)數(shù)共軛運(yùn)算。自協(xié)方差（I=K）與互協(xié)方差（I≠K）的計(jì)算式為

其中：N表示第N個(gè)傅里葉頻率。

等間距采樣的維納濾波算法利用脈沖星對的計(jì)時(shí)殘差向量，通過互相關(guān)提取共同的綜合脈沖星時(shí)信號，進(jìn)而通過多個(gè)脈沖星對取平均，進(jìn)一步消除紅噪聲、引力波與太陽系行星歷表誤差影響。維納濾波方法相對簡單，易于實(shí)施。但按照上述維納濾波算法得到的綜合脈沖星時(shí)仍然包含較強(qiáng)的高頻噪聲（主要來自于脈沖星計(jì)時(shí)殘差向量rI），還需要設(shè)計(jì)合適濾波器，進(jìn)一步濾除高頻噪聲［45］。

3 綜合脈沖星時(shí)研究結(jié)果

因綜合脈沖星時(shí)研究需要多顆毫秒脈沖星長期計(jì)時(shí)觀測資料，在21世紀(jì)初，只有2顆約連續(xù)8年的計(jì)時(shí)觀測資料及研究結(jié)果發(fā)表。利用這2顆星數(shù)據(jù)的綜合脈沖星時(shí)研究主要是加權(quán)平均與維納濾波方法［32，45-46］。結(jié)果表明，以TAI為參考的綜合脈沖星時(shí)頻率穩(wěn)定度好于任何單顆脈沖星的頻率穩(wěn)定度，且綜合脈沖星時(shí)6年以上頻率穩(wěn)定度優(yōu)于1×10?15。不同算法結(jié)果比較表明，維納濾波算法優(yōu)于加權(quán)平均算法［46］。

2012年，Hobbs等［3］發(fā)表了利用Parkes脈沖星計(jì)時(shí)陣（Parkes Pulsar Timing Array，PPTA）19顆毫秒脈沖星約17年計(jì)時(shí)觀測資料的綜合脈沖星時(shí)研究結(jié)果。PPTA早期觀測星數(shù)較少，且19顆星的觀測數(shù)據(jù)分布非常不均勻，在2000年前后約1年多的時(shí)間內(nèi)，甚至只有1顆星的數(shù)據(jù)可用。該研究結(jié)果采用基于TEMPO2軟件的廣義最小二乘擬合算法，得到采樣間隔為1年（綜合脈沖星時(shí)數(shù)據(jù)點(diǎn)間距為1年）的以TAI為參考的綜合脈沖星時(shí)EPT（PPTA11）-TAI。請參見文獻(xiàn)［3］。結(jié)果表明EPT（PPTA11）-TAI與已經(jīng)消除線性及二次項(xiàng)的原子時(shí)TT（BIPM2011）-TAI具有類似的變化趨勢，證明綜合脈沖星時(shí)正確地揭示了TAI二階以上的高階系統(tǒng)誤差。

應(yīng)該指出的是，由于脈沖星自轉(zhuǎn)參數(shù)擬合，計(jì)時(shí)觀測參考原子時(shí)的線性及二次項(xiàng)誤差被吸收到自轉(zhuǎn)參數(shù)中了，脈沖星時(shí)只能探測原子時(shí)二次以上的高階誤差。為了方便脈沖星時(shí)與原子時(shí)的比較，本文中列出的原子時(shí)都是消除了二次多項(xiàng)式的原子時(shí)系統(tǒng)。

2019年Hobbs等［20］發(fā)表了利用國際脈沖星計(jì)時(shí)陣第一次釋放數(shù)據(jù)研究得到的綜合脈沖星時(shí)結(jié)果。利用IPTA 48顆毫秒脈沖星長期計(jì)時(shí)資料，采用基于TEMPO2軟件的廣義最小二乘擬合算法（作者團(tuán)隊(duì)又稱之為“頻率分析方法（Frequentist Analysis）”），得到的綜合脈沖星時(shí)命名為TT（IPTA2016）。同時(shí)作者又從48顆毫秒脈沖星中篩選出8顆觀測數(shù)據(jù)時(shí)間跨度較長，紅噪聲較小的毫秒脈沖星，采用貝葉斯算法構(gòu)建了綜合脈沖星時(shí)。因貝葉斯算法計(jì)算量非常大，耗時(shí)多，目前只能選用少數(shù)脈沖星構(gòu)建綜合脈沖星時(shí)。8顆星貝葉斯算法結(jié)果與48顆星廣義最小二乘擬合算法結(jié)果在誤差范圍內(nèi)相一致。作者團(tuán)隊(duì)同時(shí)給出了2種算法參考TAI的綜合脈沖星時(shí) TT（IPTA2016）-TAI和 參 考 TT（BIPM2017）的綜合脈沖星時(shí)TT（IPTA2016）-TT（BIPM2017）。

圖1重現(xiàn)了文獻(xiàn)［20］由廣義最小二乘擬合得到的綜合脈沖星時(shí)TT（IPTA2016）-TAI及其誤差棒，同時(shí)繪出了原子時(shí)TT（BIPM2017）-TAI，其中MJD表示修正儒略日。可見，綜合脈沖星時(shí)TT（IPTA2016）-TAI與原子時(shí)TT（BIPM2017）-TAI變化趨勢一致，表明綜合脈沖星時(shí)TT（IPTA2016）-TAI基本上揭示了TAI的系統(tǒng)誤差。從圖1可看出，在MJD51000之前，綜合脈沖星時(shí)TT（IPTA2016）-TAI與國際原子時(shí)TT（BIPM2017）-TAI偏離較大。主要是因?yàn)樵缙诿}沖星計(jì)時(shí)TOA數(shù)量較少，且觀測誤差較大。作者給出的綜合脈沖星時(shí)數(shù)據(jù)點(diǎn)1σ單邊誤差最大者達(dá)0.6 μs，最小約0.1 μs。綜合脈沖星時(shí)數(shù)據(jù)點(diǎn)與國際原子時(shí)的偏離都在1σ誤差范圍內(nèi)。另外，2種算法得到的以TT（BIPM2017）為參考的綜合脈沖星時(shí)TT（IPTA2016）-TT（BIPM2017）具有相似的變化趨勢，這或許在某種程度上反映了TT（BIPM2017）可能存在的系統(tǒng)誤差［20］。通過太陽系行星歷表誤差對綜合脈沖星時(shí)影響分析，Hoggs等［20］認(rèn)為目前太陽系行星歷表的誤差可能是影響綜合脈沖星時(shí)頻率穩(wěn)定度因素之一。

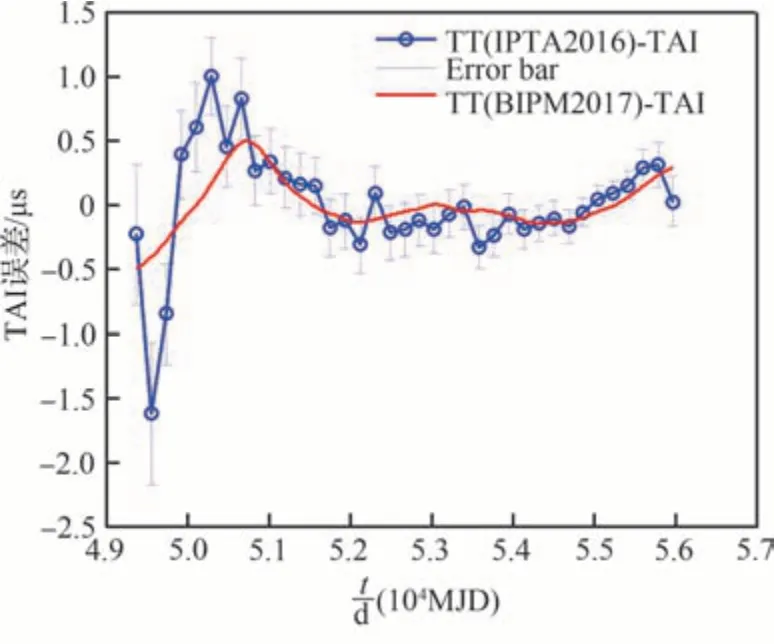
圖1 綜合脈沖星時(shí)TT（IPTA2016）-TAI與原子時(shí)TT（BIPM2017）-TAI比較［20］Fig.1 Comparison between ensemble pulsar time-scale TT（IPTA2016）-TAI and atomic time-scale TT（BIPM2017）-TAI［20］

最近，作者團(tuán)隊(duì)利用IPTA第二次釋放的毫秒脈沖星計(jì)時(shí)觀測資料［10］，采用改進(jìn)的維納濾波方法研究了綜合脈沖星時(shí)。維納濾波算法要求所有脈沖星觀測數(shù)據(jù)覆蓋相同時(shí)間跨度，并等間距采樣。所以，作者團(tuán)隊(duì)選取了具有最長共同時(shí)間跨度（約16年），且中間TOA數(shù)據(jù)中斷間隔小于400 d的10顆毫秒脈沖星。對傳統(tǒng)維納濾波算法的改進(jìn)包括：

1）對計(jì)時(shí)殘差的一次差進(jìn)行傅里葉變換，然后再除以一次差分濾波器的轉(zhuǎn)移函數(shù)［36］。試驗(yàn)證明這種方法比加平滑窗的傅里葉變換更能有效減小頻譜泄露影響。

2）采用擬合得到的冪律模型功率譜計(jì)算自（互）協(xié)方差函數(shù)。

3）等間距采樣的計(jì)時(shí)殘差仍然包含較強(qiáng)的高頻噪聲，對計(jì)時(shí)殘差進(jìn)行適度平滑，消除高頻噪聲。

利用10顆星構(gòu)建的參考TAI的綜合脈沖星時(shí)EPT-TAI結(jié)果與誤差棒繪于圖2，圖2還繪出了TT（BIPM2015）-TAI，可見EPT-TAI基本上反映了原子時(shí)TAI的系統(tǒng)誤差TT（BIPM2015）-TAI。在圖2中，綜合脈沖星時(shí)1·σ單邊誤差最大者 為0.518 μs，最 小 為0.110 μs，平 均 為0.320 μs。綜合脈沖星時(shí)誤差與脈沖星計(jì)時(shí)TOA誤差相關(guān)。進(jìn)一步減小綜合脈沖星時(shí)誤差，有待于提高TOA測量精度與加密TOA采樣數(shù)據(jù)點(diǎn)。在MJD53100附近，綜合脈沖星時(shí)與原子時(shí)偏離較大，這與維納濾波算法輸入數(shù)據(jù)（擬合后計(jì)時(shí)殘差）有關(guān)。很明顯，綜合脈沖星時(shí)所有數(shù)據(jù)點(diǎn)與原子時(shí)的偏離都在1·σ誤差范圍內(nèi)。圖1和圖2是用2種不同算法得到的綜合脈沖星時(shí)，采用的脈沖星數(shù)量與TOA時(shí)間跨度也不完全相同，但2種算法取得了類似的綜合脈沖星時(shí)結(jié)果。采用同樣方法，還計(jì)算了以TT（BIPM2015）為參考的綜合脈沖星時(shí)EPT-TT（BIPM2015）。

圖2 綜合脈沖星時(shí)EPT-TAI與原子時(shí)TT（BIPM2015）-TAI比較［10］Fig.2 Comparison between ensemble pulsar timescale EPT-TAI and atomic time-scale TT（BIPM2015）-TAI［10］

圖3是綜合脈沖星時(shí)EPT-TAI、EPT-TT（BIPM2015）、TT（IPTA2016）-TAI與 原 子 時(shí)TT（BIPM2015）-TAI頻 率 穩(wěn) 定 度（σZ［47］）的 比較。因?yàn)榫C合脈沖星時(shí)TT（IPTA2016）-TAI采樣間隔較大（相鄰采樣點(diǎn)間隔為半年），共包含37個(gè)數(shù)據(jù)點(diǎn)（見圖1），所以只能計(jì)算得到其4個(gè)σZ數(shù)據(jù)點(diǎn)。與傅里葉變換的功率譜分析相比，σZ更適合于低頻紅噪聲的分析［47］。圖3中，綜合脈沖星 時(shí)EPT-TAI、EPT-TT（BIPM2015）在t=106.9s（等于90 d）的lgσZ值偏小，這是因?yàn)樵谟?jì)時(shí)殘差數(shù)據(jù)預(yù)處理時(shí)采用了移動平均的緣故。從圖3可看出，原子時(shí)TT（BIPM2015）-TAI的σZ曲線隨時(shí)間增加，總體呈現(xiàn)上升趨勢，說明原子時(shí)高頻噪聲較小，低頻紅噪聲明顯存在。而綜合脈沖星時(shí)EPT-TAI、EPT-TT（BIPM2015）和TT（IPTA2016）-TAI的σZ曲線總體都呈現(xiàn)下降趨勢，說明與原子時(shí)相反，綜合脈沖星時(shí)存在明顯的高頻噪聲，但看不出存在低頻紅噪聲。綜合脈沖星時(shí)在t=108.4s（約等于8年）及更長時(shí)間間隔的長期頻率穩(wěn)定度接近或略好于原子時(shí)TT（BIPM2015）-TAI。因此，脈沖星時(shí)與原子時(shí)具有互補(bǔ)作用，利用脈沖星時(shí)可以改進(jìn)原子時(shí)的長期頻率穩(wěn)定度。脈沖星時(shí)長期頻率穩(wěn)定度優(yōu)于與原子時(shí)，還有待于利用更多、更長時(shí)間序列資料進(jìn)一步證明。由圖1和圖2也都能看出，原子時(shí)TT-TAI比構(gòu)建的綜合脈沖星時(shí)要平滑得多，表明原子時(shí)高頻噪聲比脈沖星時(shí)小，其短期頻率穩(wěn)定度優(yōu)于脈沖星時(shí)（見圖3）。

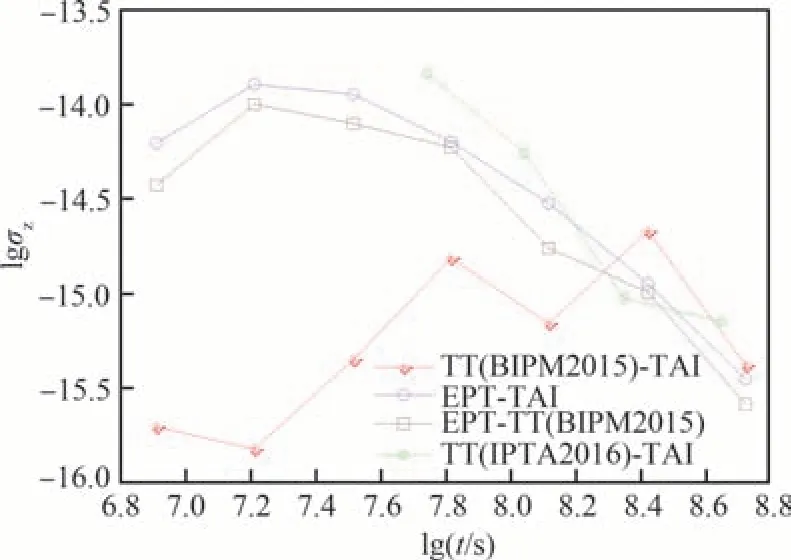
圖3 綜合脈沖星時(shí)EPT-TAI、EPT-TT（BIPM2015）、TT（IPTA2016）-TAI和原子時(shí)TT（BIPM2015）-TAI的頻率穩(wěn)定度［47］Fig.3 Frequency stability for ensemble pulsar timescales EPT-TAI， EPT-TT（BIPM2015）， TT（IPTA2016）-TAI and atomic time-scale TT（BIPM2015）-TAI［47］

有關(guān)用改進(jìn)的維納濾波算法構(gòu)建綜合脈沖星時(shí)的更詳細(xì)描述，作者團(tuán)隊(duì)也在探索中。國際上和國內(nèi)還有其他關(guān)于綜合脈沖星時(shí)研究的結(jié)果，請見參考文獻(xiàn)［48-49］。

4 總結(jié)與討論

構(gòu)建綜合脈沖星時(shí)是從多顆脈沖星長期計(jì)時(shí)觀測數(shù)據(jù)TOA中提取原子時(shí)系統(tǒng)誤差信號的數(shù)據(jù)處理過程。只有在消除DM及其變化影響、正確估計(jì)每顆星的計(jì)時(shí)噪聲、精確擬合每顆星計(jì)時(shí)模型參數(shù)情況下，才能利用合適算法提取出綜合脈沖星時(shí)信號。目前，國際原子時(shí)TAI二階以上的誤差幅度小于0.2 μs，地球時(shí)TT的誤差更小，而脈沖星計(jì)時(shí)觀測平均精度為微秒量級。所以，綜合脈沖星時(shí)算法是在具有微秒量級誤差的TOA數(shù)據(jù)中，提取幅度小于0.2 μs的信號。脈沖星計(jì)時(shí)觀測參考的太陽系行星歷表誤差，對計(jì)時(shí)殘差影響與原子時(shí)誤差影響量級上相近，來自宇宙的任何引力波可能是比原子時(shí)誤差更弱的信號，目前，利用脈沖星計(jì)時(shí)只能給出隨機(jī)背景引力波信號幅度的上限約束［50-51］。隨著脈沖星計(jì)時(shí)觀測時(shí)間長度增加，TOA觀測精度不斷提高，未來也許有可能采用更復(fù)雜的算法，同時(shí)探測原子時(shí)誤差、太陽系歷表誤差與隨機(jī)背景引力波信號［13］。

綜合脈沖星時(shí)的廣義最小二乘算法，需要將單顆脈沖星計(jì)時(shí)分析的廣義最小二乘法推廣到同時(shí)分析多顆脈沖星計(jì)時(shí)資料的情況，待擬合的參數(shù)除去每顆星計(jì)時(shí)模型參數(shù)外，再增加原子時(shí)誤差模型參數(shù)。該方法輸入數(shù)據(jù)包括每顆星的TOA序列數(shù)據(jù)、擬合后殘差與每顆星計(jì)時(shí)模型參數(shù)近似估計(jì)值。利用每顆星計(jì)時(shí)模型參數(shù)的近似估計(jì)值，將計(jì)時(shí)模型線性化。由廣義最小二乘法計(jì)算原子時(shí)誤差模型參數(shù)與每顆星計(jì)時(shí)模型參數(shù)改正值，并同時(shí)計(jì)算所有參數(shù)的協(xié)方差矩陣。綜合脈沖星時(shí)模型參數(shù)的最簡單形式就是綜合脈沖星時(shí)與原子時(shí)差值的直接采樣。為得到精確的綜合脈沖星時(shí)采樣數(shù)據(jù)點(diǎn)，需要迭代運(yùn)算。該方法的輸出數(shù)據(jù)是等間隔采樣的綜合脈沖星時(shí)數(shù)據(jù)點(diǎn)、每顆星的計(jì)時(shí)模型參數(shù)及協(xié)方差矩陣。綜合脈沖星時(shí)數(shù)據(jù)點(diǎn)采樣間隔較大時(shí)，得到的綜合脈沖星時(shí)較平滑，反之高頻噪聲較大。

綜合脈沖星時(shí)貝葉斯算法，是將單顆脈沖星計(jì)時(shí)分析的貝葉斯方法推廣到同時(shí)分析多顆脈沖星資料的情況，進(jìn)而再增加綜合脈沖星時(shí)模型參數(shù)，用貝葉斯方法同時(shí)分析得到綜合脈沖星時(shí)參數(shù)、每顆星的計(jì)時(shí)模型參數(shù)與計(jì)時(shí)噪聲模型參數(shù)。對于非線性計(jì)時(shí)模型的貝葉斯方法，其輸入數(shù)據(jù)是每顆星的TOA序列數(shù)據(jù)與計(jì)時(shí)模型參數(shù)采用值。對于計(jì)時(shí)模型線性化的貝葉斯方法，輸入數(shù)據(jù)還應(yīng)包括每顆星擬合后殘差。綜合脈沖星時(shí)模型為冪律功率譜模型，其模型參數(shù)是譜指數(shù)與譜的幅度。貝葉斯方法的輸出是每顆星的計(jì)時(shí)模型參數(shù)、計(jì)時(shí)噪聲模型參數(shù)與綜合脈沖星時(shí)模型參數(shù)。最后，由綜合脈沖星時(shí)模型參數(shù)構(gòu)建與綜合脈沖星時(shí)信號有關(guān)的多顆脈沖星總計(jì)時(shí)殘差的協(xié)方差矩陣；由每顆星的計(jì)時(shí)噪聲模型參數(shù)和綜合脈沖星時(shí)模型參數(shù)構(gòu)建與計(jì)時(shí)噪聲、綜合脈沖星時(shí)信號有關(guān)的多顆星總計(jì)時(shí)殘差協(xié)方差矩陣。再用這2個(gè)協(xié)方差矩陣按照式（29）構(gòu)建綜合脈沖星時(shí)波形，按照式（30）計(jì)算綜合脈沖星時(shí)的協(xié)方差。最后得到的綜合脈沖星時(shí)波形數(shù)據(jù)點(diǎn)分布與多顆星總計(jì)時(shí)殘差數(shù)據(jù)點(diǎn)分布相同。受脈沖星計(jì)時(shí)白噪聲影響，綜合脈沖星時(shí)包含較大白噪聲，進(jìn)一步平滑處理是必要的。

與前二者不同，綜合脈沖星時(shí)的維納濾波算法首先是利用計(jì)時(shí)觀測資料，分別對每顆脈沖星進(jìn)行計(jì)時(shí)分析，獲得每顆星擬合后計(jì)時(shí)殘差，并對擬合后計(jì)時(shí)殘差進(jìn)行預(yù)處理，進(jìn)一步得到等間隔采樣的計(jì)時(shí)殘差數(shù)據(jù)。并將此作為維納濾波算法的輸入數(shù)據(jù)。維納濾波的特點(diǎn)是利用預(yù)處理后計(jì)時(shí)殘差，計(jì)算每顆星殘差的自協(xié)方差矩陣與不同脈沖星殘差之間的互協(xié)方差矩陣，從而構(gòu)建維納濾波器。最后按照式（31）由每顆星等間隔采樣的殘差加權(quán)計(jì)算得到綜合脈沖星時(shí)。維納濾波算法輸出數(shù)據(jù)就是綜合脈沖星時(shí)采樣數(shù)據(jù)點(diǎn)，其采樣間隔與每顆星預(yù)處理后的殘差間隔相同。由于脈沖星計(jì)時(shí)殘差包含較大白噪聲，為進(jìn)一步削弱白噪聲影響，還需要對維納濾波得到的綜合脈沖星時(shí)進(jìn)行平滑處理。利用維納濾波器與任何單顆星計(jì)時(shí)殘差，還可以按照式（31）提取該單顆星的脈沖星時(shí)信號。綜合脈沖星時(shí)誤差由多顆星各自的脈沖星時(shí)信號加權(quán)平均的彌散度估計(jì)得到。

至今，所有已經(jīng)發(fā)表的以TAI為參考的綜合脈沖星時(shí)都能檢測到TAI系統(tǒng)誤差TT-TAI。文獻(xiàn)［20］故意將TAI系統(tǒng)誤差TT-TAI放大到2倍，得到假設(shè)的試驗(yàn)性時(shí)間尺度，用該試驗(yàn)時(shí)間尺度為參考構(gòu)建的綜合脈沖星時(shí)還能夠檢測到2倍的TT-TAI系統(tǒng)誤差。利用同樣的脈沖星計(jì)時(shí)觀測資料，以地球時(shí)TT為參考構(gòu)建的綜合脈沖星時(shí)EPT-TT具有幅度更小的系統(tǒng)性變化。因?yàn)槿狈Ρ萒T更理想時(shí)間尺度作比較，EPTTT的誤差主要來自于TT還是EPT，目前尚難確定。采用多種不同算法，利用不同計(jì)時(shí)觀測資料構(gòu)建EPT-TT，并進(jìn)行互相比較，也許能夠進(jìn)一步揭示EPT-TT系統(tǒng)誤差來源。以國際原子時(shí)TAI為參考構(gòu)建的綜合脈沖星時(shí)EPT-TAI是獨(dú)立于TT-TAI的時(shí)間尺度，有可能作為地球時(shí)TT的另一個(gè)版本投入應(yīng)用［3，20］。從未來的實(shí)際應(yīng)用考慮，除去研究綜合脈沖星時(shí)EPT-TAI構(gòu)建方法（算法）外，還需要進(jìn)一步研究綜合脈沖星時(shí)的保持方法，即在構(gòu)建EPT-TAI基礎(chǔ)上，不斷利用新的TOA觀測資料延展并保持綜合脈沖星時(shí)系統(tǒng)的問題。

目前，綜合脈沖星時(shí)短期頻率穩(wěn)定度低于TAI，主要來自于較大的TOA測量誤差。通過設(shè)計(jì)合適的濾波器，進(jìn)一步濾除綜合脈沖星時(shí)的高頻分量，只保留需要的低頻信號，可以改進(jìn)綜合脈沖星時(shí)的短期頻率穩(wěn)定度。雖然少數(shù)輻射信號較強(qiáng)、觀測信噪比較高的毫秒脈沖星TOA測量精度最終會受到脈沖相位抖動的限制［52-53］，但對輻射信號較弱的大部分脈沖星，利用高靈敏度的設(shè)施能夠不斷提高TOA測量精度。例如中國FAST對毫秒脈沖星TOA的測量精度達(dá)到約0.05 μs，這將會明顯改進(jìn)未來綜合脈沖星時(shí)的短期頻率穩(wěn)定度水平。綜合脈沖星時(shí)的長期頻率穩(wěn)定度與地球時(shí)TT可比，甚至更好。隨著脈沖星計(jì)時(shí)觀測資料時(shí)間跨度增加，將會進(jìn)一步驗(yàn)證綜合脈沖星時(shí)長期穩(wěn)定度水平。