雙排鋼板樁圍堰受力與計算方法研究
沈 印,游劍南
[1.上海市政工程設計研究總院(集團)有限公司,上海市 200092;2.江陰市防汛防旱服務中心,江蘇 江陰 214431]
0 引言
雙排鋼板樁圍堰具有占地面積小、施打及拆除方便、對河道水質影響小等優點,在擋水高度不太高的情況下相對于傳統土石圍堰具有明顯的優勢,在全國各地水利項目施工導截流期間得到了廣泛的使用。但由于僅作為臨時結構,往往根據經驗進行設計或由施工單位自行設計,對于該種結構的計算尚缺乏研究。若要得到準確的內力及變形結果,需用有限元進行分析,無法滿足廣大設計人員的現實需求。因而易發生過設計或欠設計的情況,即圍堰斷面過大、樁長過長,造成不必要的浪費;或者施工期間圍堰變形過大、透水嚴重,影響堰內結構施工的情況。本文將在傳統土壓力理論及豎向彈性地基梁計算方法的基礎上對雙排鋼板樁的受力及計算方法進行分析研究,并通過與有限元法的比較驗證了本文的計算結果。
1 雙排鋼板樁內力計算總體思路
由于雙排鋼板樁設計參數較多,為便于計算分析,本文對該結構進行了一些假定。(1)假定樁間拉桿數不超過2 根。(2)假定外河側水位不高于上側拉桿,內河側水位不高于下側拉桿。在此基礎上,樁間填土采用主動土壓力公式計算并考慮有限空間的影響,泥面以下樁基內力采用豎向彈性地基梁進行計算,泥面以上樁基內力可分段求解并通過材料力學公式計算。計算中共存在兩個未知數分別為兩根拉桿的拉力。最終可通過在拉桿作用點前后排樁間距離的變化量等于拉桿伸長量列出兩個方程并求出拉桿拉力。結構計算圖示如圖1 所示。
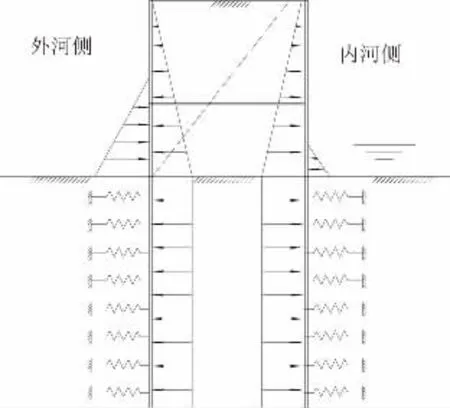
圖1 雙排鋼板樁圍堰計算圖示
2 有限空間土壓力計算
在鋼板樁間距較大的情況下,雙排鋼板樁內填土產生的土壓力可采用無限空間土壓力理論計算。但當鋼板樁間距較小時,需考慮滑動土體受前后排樁的限制作用,采用有限空間下的土壓力計算方法。考慮有限空間內的土壓力需采用庫倫土壓力理論,具體推導過程如下:
由于鋼板樁為直立,且滑動摩擦系數較小,可假定為墻背光滑且土體與墻背的摩擦角為0°,在不考慮黏聚力的情況下,無限空間庫倫土壓力計算圖示如圖2 所示,計算公式如下[1]:
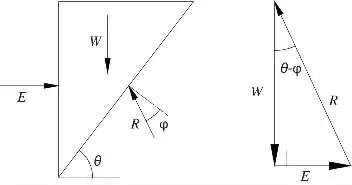
圖2 庫倫土壓力計算圖示
式中:E 為主動土壓力,kN;W 為滑動土體自重,kN;ψ 為土體內摩擦角;H 為填土高,m。
此種情況下可以求出當θ=45°+ψ/2 時,土壓力最大,故此角度為主動土壓力的破裂角。
當土體受后方結構限制時,主動土壓力圖示如圖3 所示。公式推導過程如下:
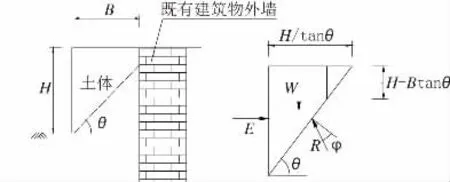
圖3 有限空間庫倫土壓力計算圖示
對E 求θ 的導數,從而求得E 最大時的θ 值:
該θ 值即有限空間下的庫倫土壓力滑動摩擦角。同樣可求得有黏聚力C 時的庫倫土壓力滑動摩擦角計算公式,具體計算圖示如圖4 所示。推算過程如下:
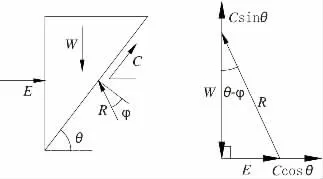
圖4 考慮黏聚力后有限空間庫倫土壓力計算圖示
至此,已可根據鋼板樁內填土參數、填土高度求出任意前后排樁間距下鋼板樁所受的主動土壓力。
3 泥面以下樁身內力計算
泥面以下樁身內力和變形計算采用豎向彈性地基梁的方法,計算推導過程如下:根據樁的繞曲線微分方程[2]:
則邊界條件為:
式中:δVV、δVM、δMM稱為柔度系數;H0、M0為泥面以上樁身所受合力,其中包括土壓力、水壓力及拉桿拉力。
推算得基坑底以下深度z 處鋼板樁水平剪力V、彎矩M、轉角θ、位移y 分別為:
泥面處的樁身內力及變形計算值為含有拉桿拉力值的計算式。
4 泥面以上樁身內力計算
由于樁身受力非連續的特性,泥面以上樁身內力需進行分段計算,每段均通過材料力學公式EIω"=M列出各段的位移ω 及轉角ω’公式,利用各段在分界點處的位移ω 及轉角ω’與相鄰段一致求出位移及轉角公式中的常數。通過與泥面處樁身位移的關系式求出樁身各點位移為:
式中:x0為樁身泥面處的位移值,m;θ0為樁身泥面處的轉角值,°。
最終通過前后排樁在拉桿處的位移差等于拉桿伸長量求出拉桿拉力值。
泥面以上鋼板樁受力圖示如圖5 所示。
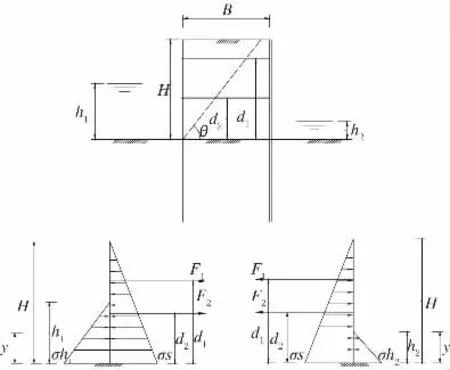
圖5 泥面以上鋼板樁受力圖示
泥面以上位移計算過程如下:
當y≤d2時
同理,求得第三段h1<y<d1,第四段d1<y 時各點的位移。
根據拉桿點前后排樁位移值的差等于拉桿的伸長量可列出二元一次方程組:
式中:EA 為拉桿變形參數,kN;L 為拉桿長度,m;
解方程組得F1:
在求出F1、F2后,需進一步判斷是否符合實際情況。如果求出的拉桿拉力為負值,說明該拉桿不受力,可簡化為單根拉桿的結構進行復核計算。
5 計算結果校核
為校對本次計算程序的準確性,與ansys 有限元軟件計算結果進行了比對分析,選取的設計參數見表1。
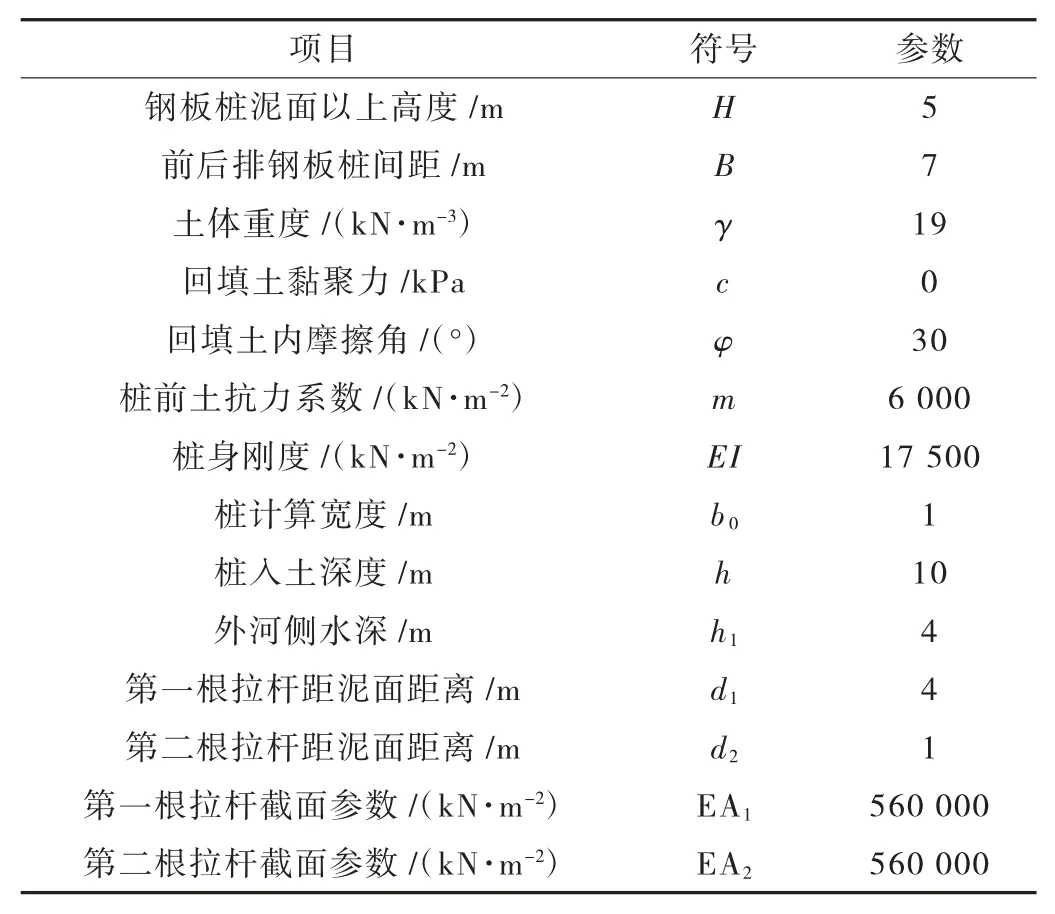
表1 復核計算參數
分別采用有限元法及本文方法的計算結果比較見表2。
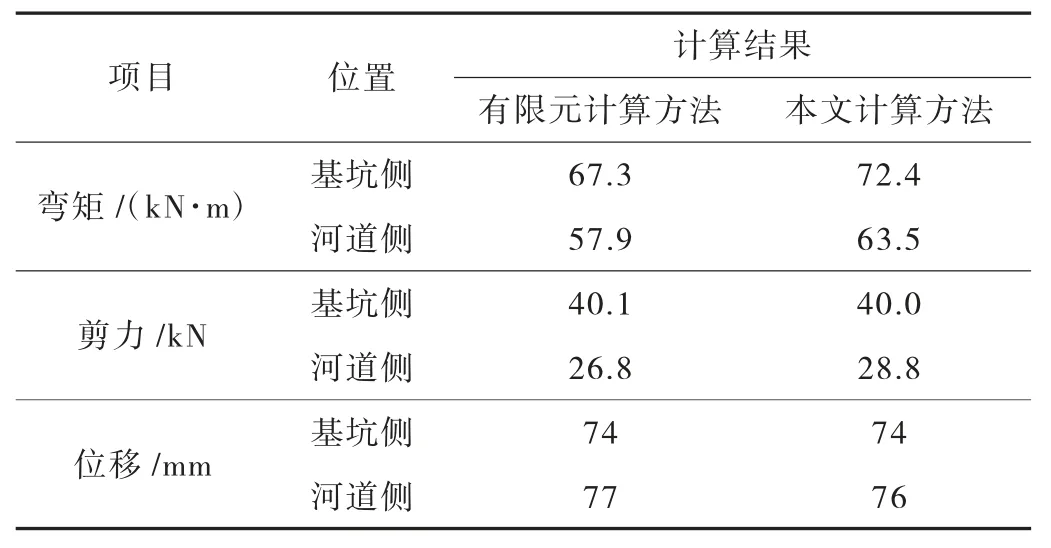
表2 計算結果對比
從表2 可知,本文的計算結果與有限元法的計算結果基本一致,驗證了本文計算方法的準確性。
6 結論
本文首先在傳統土壓力理論基礎上推算出了在雙排鋼板樁內有限空間下的土壓力計算方法。其次利用豎向彈性地基梁法推算出了泥面以下樁身內力及位移的計算方法。再次利用材料力學公式及前后排樁在拉桿處變形方程式求出了拉桿拉力,從而解出了樁身各點的內力及位移。最后通過與有限元法的比較驗證了本文方法的準確性。由于本文計算方法完全可以在Excel 內實現程序化,相較有限元法可大幅降低設計難度、提高設計效率。

