沖擊載荷下頻率響應函數的高斯過程回歸方法

任 程，劉世洲，郜 偉，張二亮

(鄭州大學 機械與動力工程學院， 鄭州 450001)

0 引言

頻率響應函數(frequency response function,FRF)是機械系統動態特性評估、振動控制和故障診斷等的有力工具。使用力錘對結構施加沖擊載荷，是測量頻響函數的重要方式，具有操作簡單、成本低和效率高等優點，在機械、土木和航空航天等工程領域得到了廣泛應用[1]。因此，開展沖擊載荷下頻響函數的高精度辨識方法研究具有鮮明的工程應用背景和價值。

基于力錘沖擊的FRF測量及其應用已經在諸多學術專著中予以詳細介紹。影響沖擊載荷下FRF測量的關鍵因素包括力錘沖擊頭材質選取、實驗方案設計(例如預觸發確定)以及信號采集等[2]。Bediz等[3]設計了一種用于微型結構模態實驗的沖擊激勵系統，具有可重復、高帶寬和沖擊力可控等優點。Xia等[4]開展了玻璃鋼拉索的沖擊振動實驗，采用半功率點法計算實驗模態阻尼。針對大型結構的動態特性測量，Tian等[5]提出了基于非接觸視覺測量的移動沖擊測試方法，以識別整個結構的模態振型和柔度矩陣。

譜估計方法直接從測量的輸入輸出數據中計算FRF，是錘擊法測試中開展FRF估計的主要方法。從算法角度考慮，窗函數設計是影響FRF譜估計精度的主要因素。基于譜估計方法的計算過程，Yang等[6]建立了插值和瞬態誤差的非參數模型，分析了窗函數對兩種誤差的影響。針對譜估計窗函數帶來的插值和瞬態誤差，Shao等[7]提出了一種迭代補償方法，用于提高沖擊載荷下頻響函數的辨識精度。然而，譜估計方法完全依賴于測量數據，FRF的估計精度極易受到測量數據長度和質量的影響。

高斯過程回歸(gaussian process regression,GPR)使用無限維多變量高斯分布對函數進行直接建模，已經發展成為一種根據經驗樣本學習映射關系的非參數高效數據驅動建模方法[8]。相對于經典的譜估計方法，GPR不僅利用了樣本數據，還能融合函數模型的固有性質；相比于傳統的參數化建模方法，GPR在模型選擇方面具有更多靈活性，能夠更好地適應數據的變化。高斯過程的性質與其協方差函數(即核函數)有著密切聯系。通過刻畫系統脈沖響應函數的固有性質(例如光滑、穩定)，基于最大熵原理，穩定樣條、對角相關等核函數被相繼提出和發展，在系統與控制領域內發展了傳遞函數的正則化估計方法[9-12]。

本文將系統和控制領域的正則化方法引入實驗模態分析領域，較為系統地給出了沖擊載荷下FRF估計的GPR理論與方法。針對機械系統階次高及低階阻尼小的特點，豐富了FRF的復高斯過程先驗模型。基于貝葉斯推斷框架，利用GPR模型給出了FRF的最大后驗估計及其方差，并借助QR分解改善了復高斯過程超參數優化的數值正定性。最后，通過開展平板沖擊仿真和葉片振動實驗，驗證了本文方法的有效性和可靠性。

1 問題描述

在實際的工程測試中，采集的信號都是時域的離散信號，采用離散傅里葉變換(discrete fourier transform,DFT)將時域信號x[t],t=0,1,…,N-1變換到頻域X(k)，

(1)

式中：k=0,1,…,N/2， j2=-1。

對于線性時不變動態系統，沖擊激勵u[t]和系統響應y[t]的DFT頻譜關系如圖1所示，可表示為

Y(k)=G(ωk)U(k)+V(k)

(2)

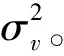
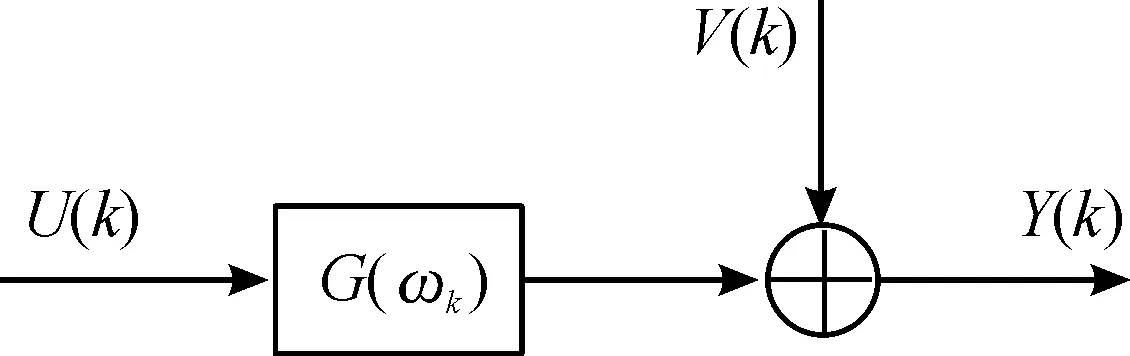
圖1 DFT頻譜關系

當響應信號采集不完整時，在關系中需要引入額外的瞬態項，用于描述非周期信號傅里葉變換帶來的泄露誤差[13]。若激勵信號具備粗糙性質，該瞬態項可以通過連同FRF一起辨識的方式來剔除。然而，沖擊激勵的頻譜是光滑的，無法分離瞬態項和FRF，則需要通過施加指數衰減窗函數來抑制泄露誤差。因而，沖擊載荷下的數據采集樣本長度應盡可能足夠長。

從測量數據Z={(U(k),Y(k)),k=1,2,…,F}(直流分量和奈奎斯特頻率除外)中，使用GPR模型對FRF進行高精度建模和估計，是本文要解決的問題。

2 非參數辨識方法

2.1 復高斯過程

基于貝葉斯觀點，本文將FRF視作頻域上的復值隨機函數。進一步，假設FRF是頻域上的復高斯向量，即G服從多元復高斯分布。

一般來說，機械結構的FRF在所關心的頻帶內具有模型復雜度較高、低階阻尼較小得的特點，導致其建模難度大，這要求復高斯過程具備較強的泛化能力。為此，不同于常用的零均值假設[9-12]，本文通過引入FRF的先驗均值函數，使復高斯過程充分融合系統的先驗信息。復高斯向量G可表示為

G=Gp+ΔG

(3)

式中：Gp為FRF的先驗均值函數，ΔG服從零均值多元復高斯分布。

先驗均值函數Gp可以借助模態參數識別方法得到。例如，采用PolyMAX方法從測量數據Z中確定動態系統的某些極點pr，再將pr應用于FRF的極點-余項模型，確定模態常數Ar和殘余項AU、AL，則

(4)

式中，上標*表示復共軛。

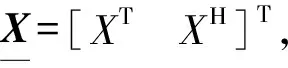
(5)

(6)

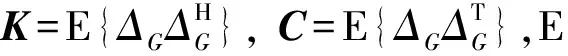
(7)

需要注意的是，核函數K和關系函數C滿足K(ωk,ωl)=C(ωk,ω-l)。

高斯過程的核函數刻畫了待建模系統的物理信息，在回歸分析中起著決定性的作用。對角相關核函數是在系統和控制領域使用最為廣泛的核函數之一，描述了脈沖響應的光滑、穩定等基本性質。因此，本文采用對角相關核函數對FRF開展復高斯過程建模，其頻域表達式為

(8)

式中：比例因子γ∈R+和核參數α,β∈R+稱為超參數。

2.2 似然函數

根據中心極限定理和輸出噪聲的獨立同分布假設，當數據量F→∞時，干擾噪聲的DFT頻譜是圓形復高斯分布，其關系矩陣為零矩陣。為了與式(5)一致，FRF的似然函數寫成如下形式

(9)

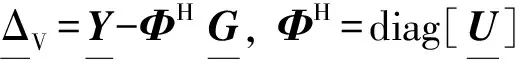
2.3 最大后驗估計

(10)

式中：∝表示正比于，概率密度函數p(θ)通常假設為均勻分布。

最大后驗概率估計常用于參數的推演。聯合式(5)(9)和(10)，FRF的后驗分布仍為復高斯分布，其最大后驗概率估計為

(11)

(12)

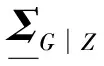
2.4 超參數優化

超參數θ是未知的，需要從測量數據Z中學習獲得，通常采用極大邊際似然估計方法。邊際似然函數可視作似然函數在先驗分布上的期望分布，它能夠自動權衡數據擬合精度與模型復雜程度。超參數θ的極大似然估計為

(13)

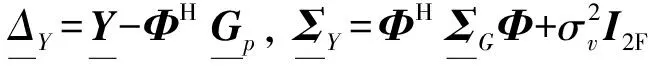
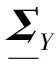
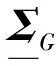
(14)

式中：L是下三角矩陣。根據Woodbury矩陣求逆公式和Sylvester行列式定理可得

(16)

受到式(15)(16)啟發，構造如下矩陣，并將其改寫成QR分解式，

(17)

式中：Q為正交矩陣，R1為2F維上三角方陣，R2為2F維列向量，r為標量。基于式(17)可以得到

(18)

(19)

(20)

最后，目標函數J(θ)可以化簡為

(21)

采用基于梯度的優化算法對目標函數進行最小化，目標函數J(θ)關于超參數θ的偏導數為

(22)

(23)

(24)

式中，Tr表示矩陣求跡運算。

基于式(21)和(22)，使用Matlab的優化工具箱中fmincon函數進行尋優計算，便可獲得最優的超參數估計。該求解器可用于求解約束非線性多元函數最小值，包含內點優化、SQP優化和信賴域反射優化等不同類型的算法。

最后，根據超參數的最優估計值，結合式(11)和(12)即可獲得FRF的估計及其方差，完整的算法流程如圖2所示。

3 算例與實驗

3.1 數值算例

為了驗證本文方法的有效性和可靠性，開展沖擊載荷下簡支平板的FRF估計。平板的彈性模量為200 GPa，尺寸為1 m×1 m×0.002 m，密度為7 850 kg/m3，泊松比為0.3。在中心位置施加沖擊載荷，采用模態疊加法生成系統響應(本算例以速度作為響應)，添加高斯白噪聲來模擬測量數據，如圖3所示。使用的采樣頻率為1 024 Hz，感興趣的頻帶取1～300 Hz，數據樣本量F=300。

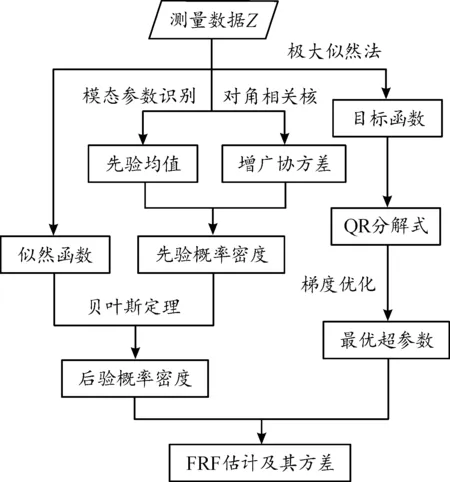
圖2 沖擊載荷下FRF的GPR方法流程框圖

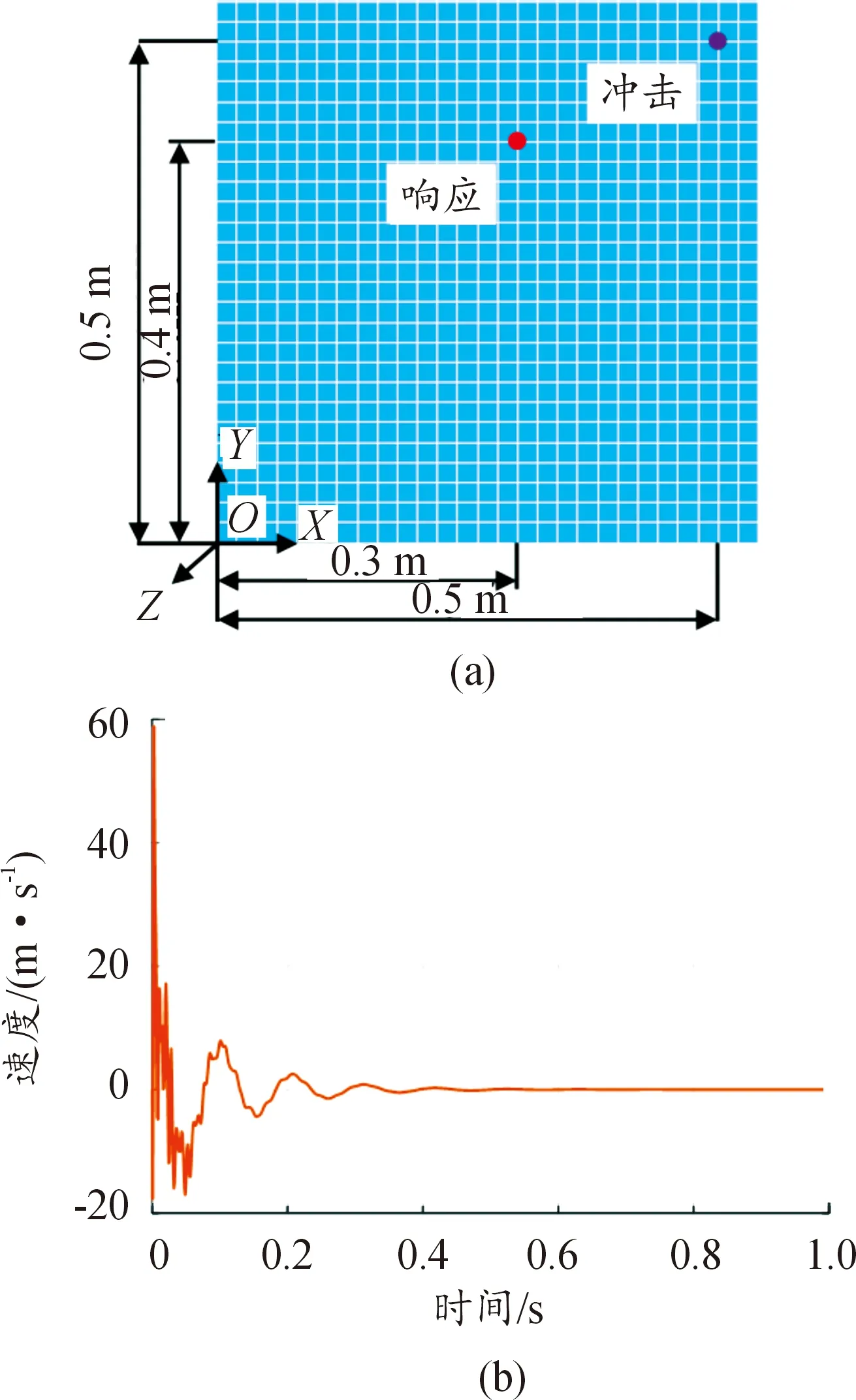
圖3 平板1/4有限元模型 (a)和無噪聲響應波形(b)

為了提高仿真運算結果的可靠度，以及對仿真得到的結果進行評價，可進行多次的蒙特卡洛模擬。基于蒙特卡洛模擬，計算均方誤差(mean-square error,MSE)對FRF的估計結果進行評價，

(25)

為了顯示更寬的數值范圍，本文使用分貝(dB)作為FRF幅值和MSE的單位。dB是振動、聲學和電信等研究領域常用的無量綱量，可定義為2個數值(測量值X和參考值X0)的對數比率，

1 dB=20lg|X/X0|

(26)

式中，默認參考值X0=1。

考慮響應信號的信噪比(signal-to-noise ratio,SNR)為10 dB的情形，分別使用譜估計方法和本文方法對平板的FRF進行估計，結果如圖4所示。與譜估計方法相比，由于借助復高斯過程對FRF的固有性質(光滑、穩定)進行刻畫和融合，本文方法可以獲得更小的MSE值，FRF的估計精度更高，證明了其有效性。

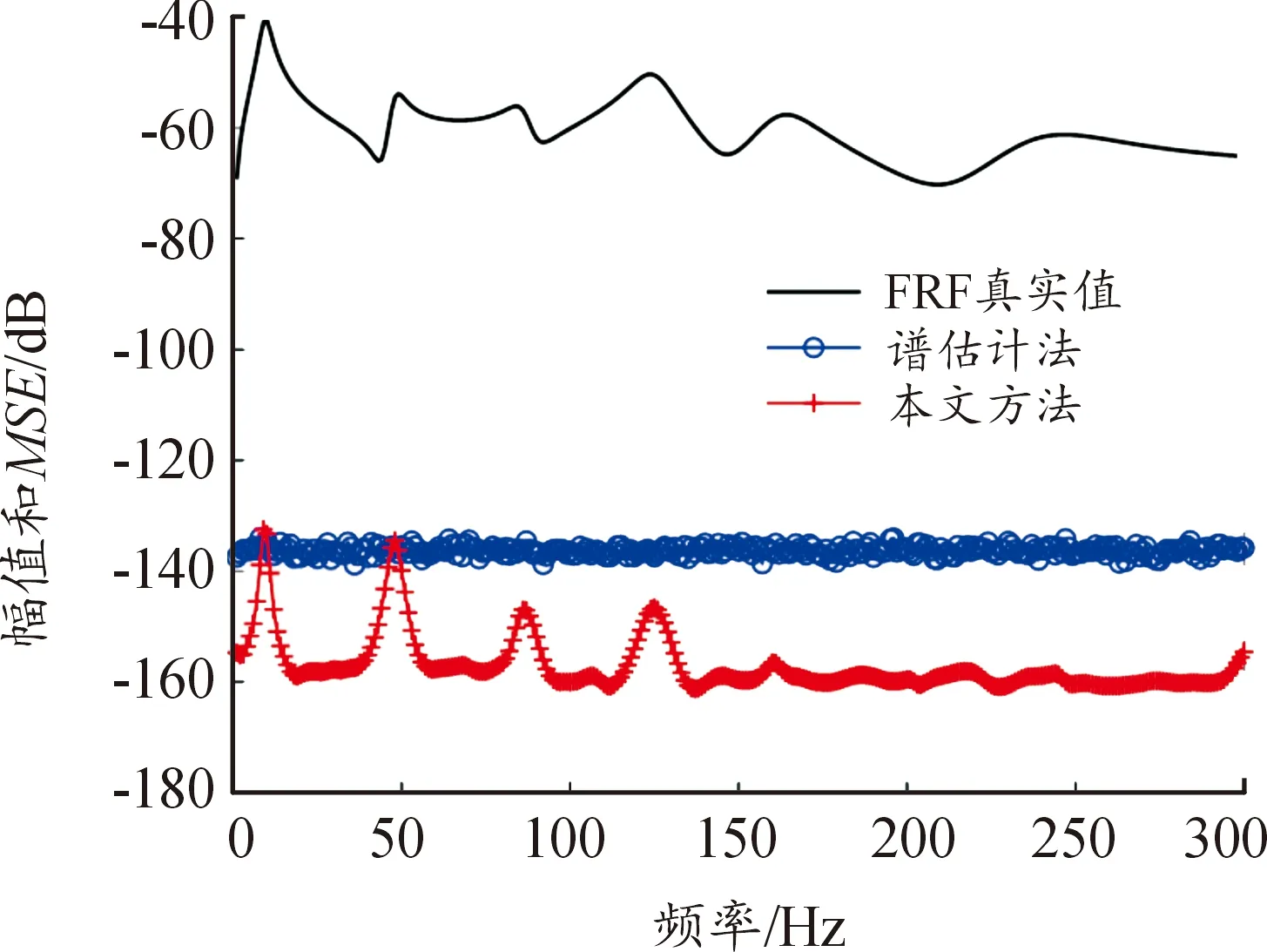
圖4 平板的FRF估計曲線

令式(25)在所有關心頻率上取平均，進一步考慮不同SNR情形，MSE均值的計算結果如圖5所示。相比于譜估計方法，本文方法在不同的噪聲水平下均能夠獲得更高精度的FRF估計結果，且在低SNR(例如-10 dB)的嚴苛環境下效果更為顯著，證明了其可靠性。

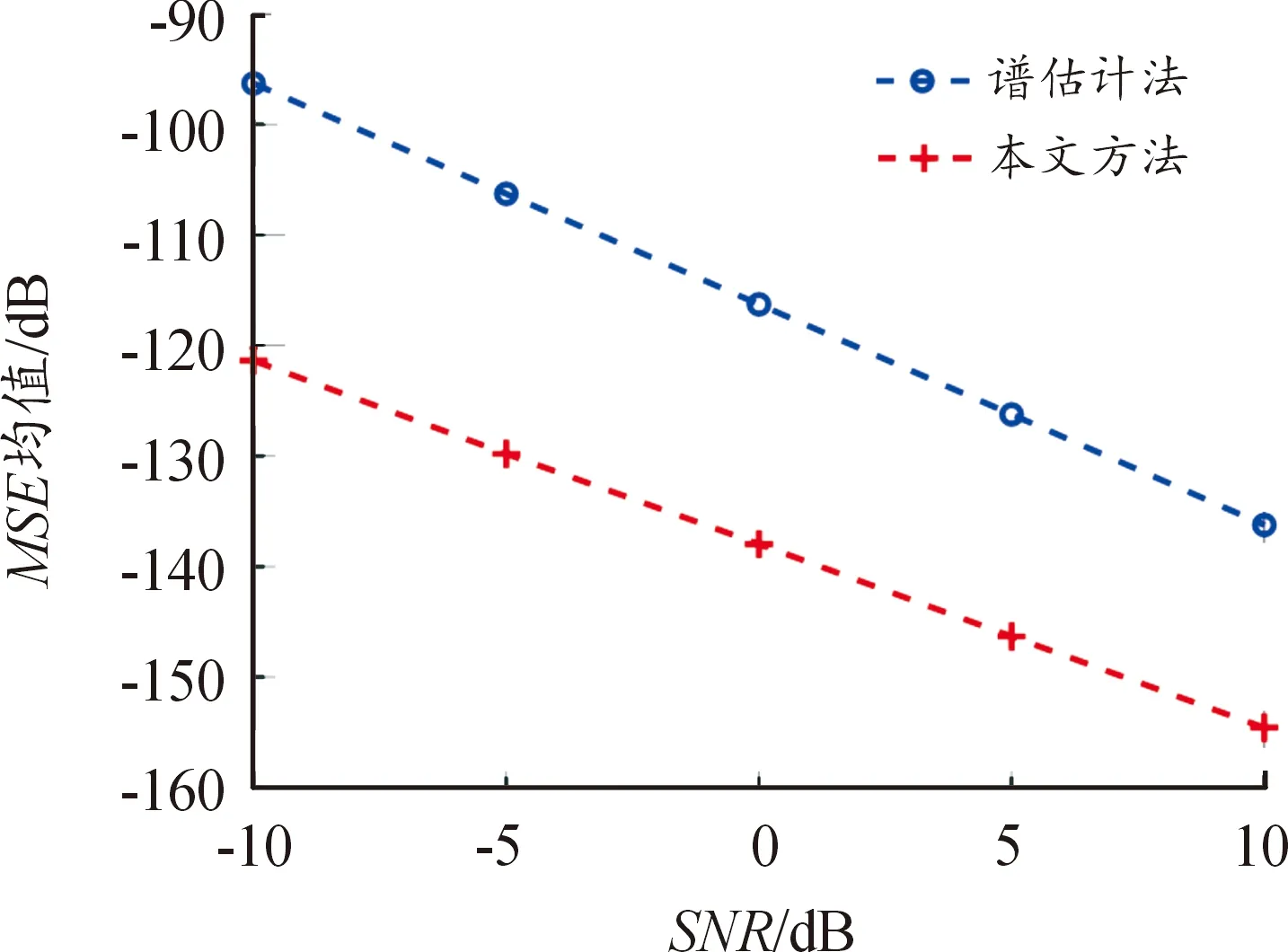
圖5 不同SNR下的MSE均值

3.2 振動實驗

以長約44 cm的無人機螺旋槳葉片為例，開展錘擊振動實驗，驗證本文方法的實際應用效果。使用PCB 086C03模態力錘激振葉片，利用數字圖像相關VIC-3D高速攝像系統測量葉片的振動響應，如圖6所示。高速攝像機型號為Photron FastCam Mini UX100，配備了Nikon 60 mm f/2.8 D廣角鏡頭，板載內存容量為8 GB，分辨率為1 024像素×576像素，曝光時間為0.25 ms，并以2 000 fps的幀率進行拍照記錄。VIC-3D高速攝像系統的位移測量精度約為6 μm，本實驗直接采用位移作為系統響應。

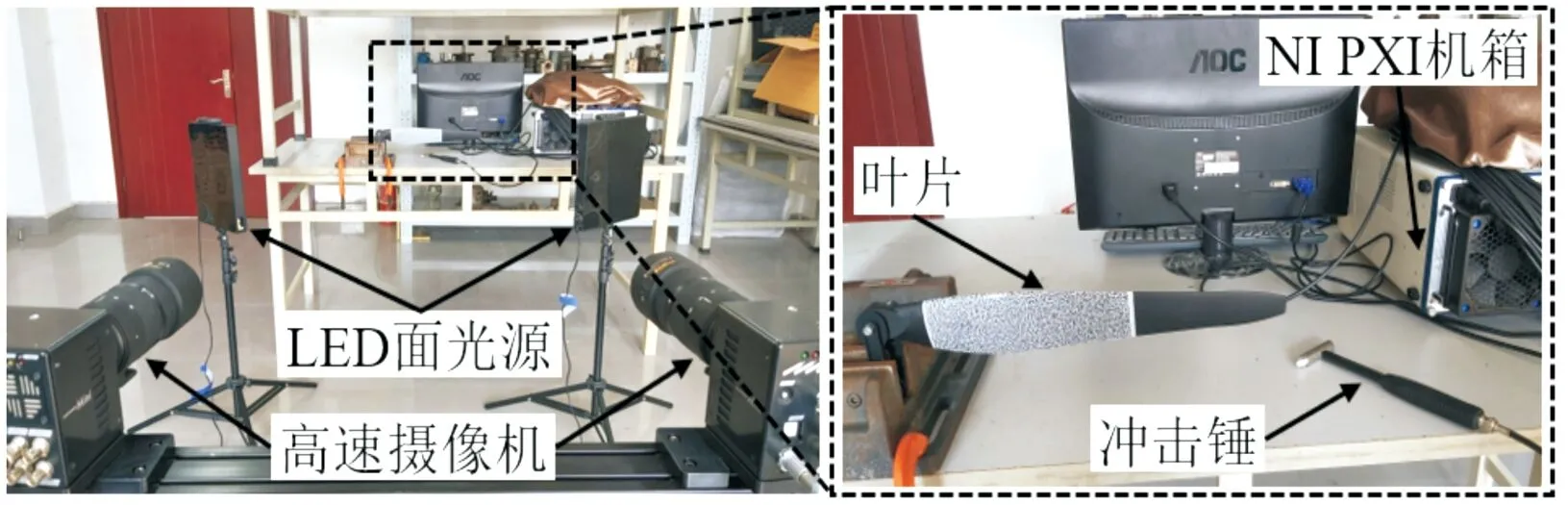
圖6 葉片振動實驗

為了進一步抑制噪聲干擾和減少頻譜泄露，本實驗對時域信號進行加窗處理：沖擊信號施加單位增益窗，響應信號施加指數窗。經過加窗處理的時域信號波形如圖7所示。

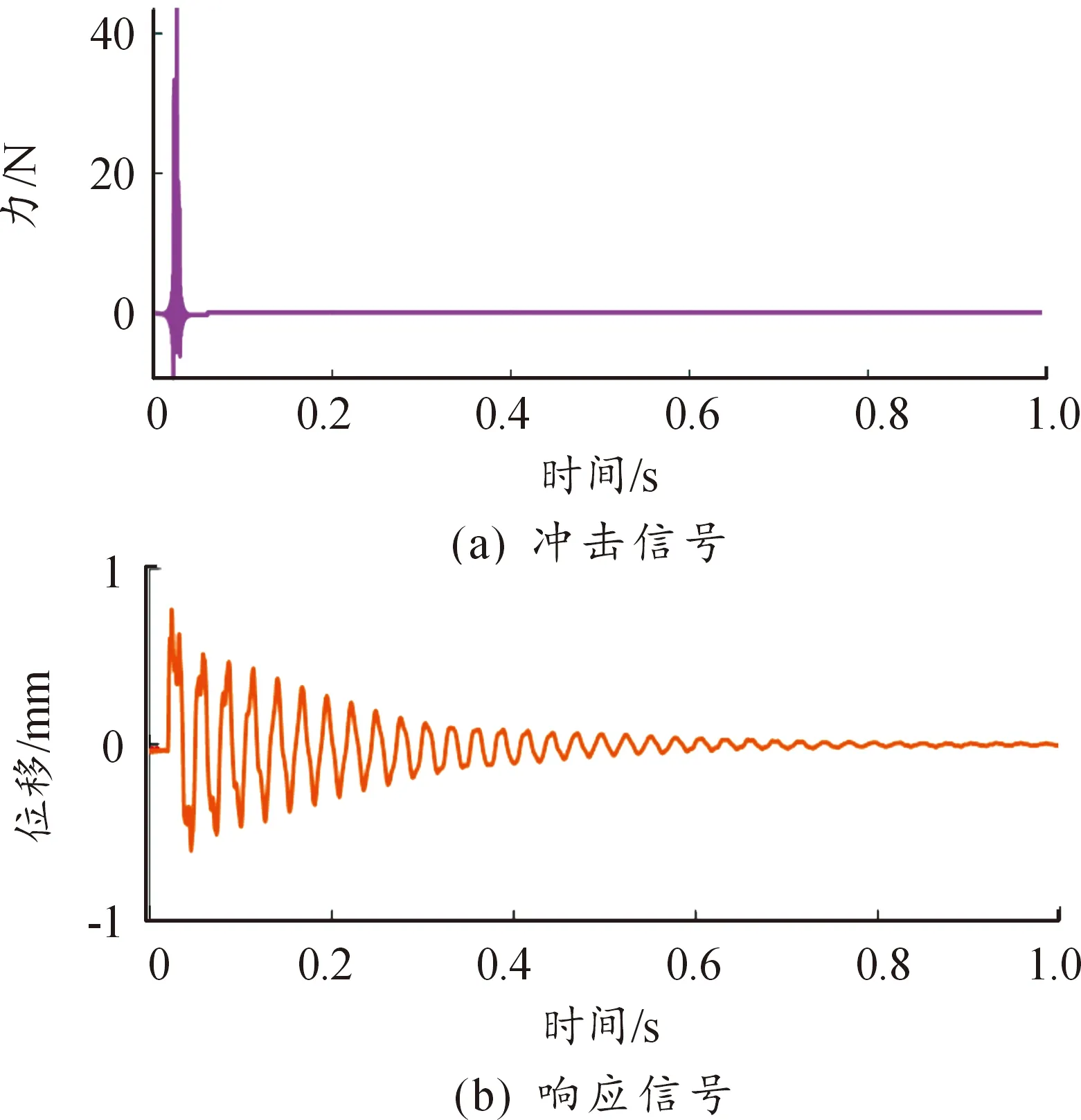
圖7 加窗后時域信號波形

選取感興趣的頻帶為1～400 Hz，F=400。分別采用譜估計方法和本文方法對螺旋槳葉片的FRF進行估計，結果如圖8所示。2種方法估計的FRF基本吻合，但相較于譜估計方法，由于借助先驗信息和全局建模的優勢，本文方法估計的FRF波動更小，即隨機擾動更小。此外，FRF的譜估計在145 Hz附近存在異常凸起，這極可能是高速相機風扇運轉產生的噪聲峰值[16]，本文方法則能獲得更加準確的FRF估計。

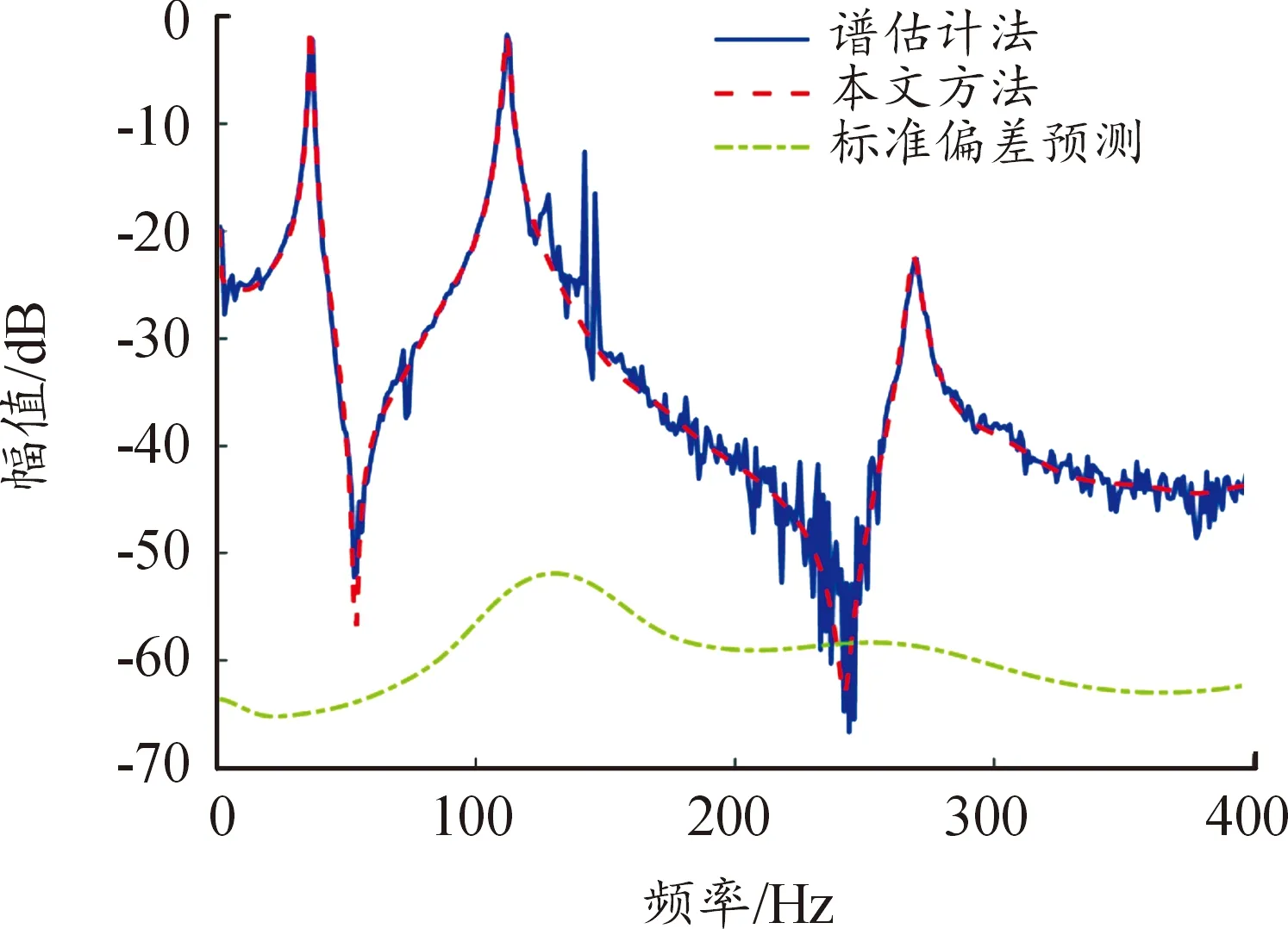
圖8 葉片的FRF估計曲線

根據式(12)預測了FRF估計的標準偏差，反映了FRF估計的精度，同時刻畫了FRF估計的不確定度在頻域的分布情況，在120～150 Hz附近不確定度最大，與該頻段存在異常噪聲的事實相切合。

4 結論

為了提高沖擊載荷下實驗模態分析的精度，本文發展了一種基于GPR方法的FRF非參數辨識方法。該方法利用貝葉斯學習技術融合了測試系統的樣本信息和模型信息，給出了FRF的最大后驗估計及其方差，其有效性和可靠性在平板沖擊仿真和葉片振動實驗中得到了驗證。相比于經典的譜估計方法，本文提出的方法具有更高的FRF估計精度，同時還可給出FRF估計的不確定度描述，為模態測試等領域提供了有力的工具。在下一步工作中，將致力把該方法擴展至有色噪聲情形。