一種對極數互質的高精度絕對式角位移傳感器

吳昶亮,于治成，蒲紅吉，展丙男，樊星辰

(1.重慶理工大學 機械檢測技術與裝備教育部工程研究中心， 重慶 400054；2.北京理工大學 機械與車輛學院， 北京 100081；3.合肥工業大學 儀器科學與光電工程學院， 合肥 230009)

0 引言

精密角位移傳感器在精密運動控制領域廣泛應用，如智能機器人、航空航天、半導體器件制造等領域[1-2]。隨著科學技術的進步和角位移傳感器應用要求的提高，傳感器不僅需要精度高，還要能提供角位移的絕對位置測量。當前有多種類型的傳感器可以實現絕對式角位移測量，應用較廣的有磁場編碼器、光柵編碼器和電容式傳感器[3-5]。絕對式磁場編碼器通常應用于粉塵污染嚴重或機械振動較大等惡劣工作環境，但其測量精度較低，難以完成高精度角位移測量[6-7]。

光柵編碼器可以實現超高精度的測量,且具有高分辨率、壽命高、抗干擾能力強等優點，在高性能數控機床等精密測量領域應用廣泛。絕對式光柵編碼器的內部碼盤分為精碼道和粗碼道，精碼道的刻畫相比于粗碼道更加精密，直接決定光柵編碼器的精度；粗碼道在編碼器整周無重復編碼，保證碼盤在整周任意位置編碼唯一，從而實現光柵編碼器的絕對位置測量[8-9]。光柵編碼器的測量精度和分辨率完全取決于精碼道上刻畫柵線的精密程度，但由于超精密光刻和高穩定高倍數細分上的限制，已經進入了發展的瓶頸期[10]，并且在光柵編碼器的粗碼道設計過程中，不僅要保證無重復位置編碼，還要考慮編碼的容錯、易處理等多方面因素[11]。此外，光柵編碼器對工作環境要求較高，難以在惡劣條件下應用[8,12]。

電容式角位移傳感器采用平板電容器作為傳感元件，兩組電容極片的相對有效面積決定了電場的強度，而且電容式傳感器的整個平面面積都可以覆蓋電容極片，可以輸出較強的信號，在受到機械安裝或者震動影響時，電容式傳感器會表現出更強的抗干擾能力。另外，電容式傳感器結構相對簡單，大大降低了制造要求和成本[13]。時柵傳感器利用時間量完成空間位移測量，不同于光柵傳感器依賴超精密光刻技術，極片加工工藝成熟簡單，降低了制造難度[14-16]，且時柵傳感器在刻畫精度不及光柵傳感器的情況下采用時鐘脈沖插補空間脈沖來保證高分辨率[17]，在精密測量領域具有很高的發展前景。

本文中提出了一種基于時柵測量原理的高精度電容式絕對角位移傳感器，實現了高精度角位移測量的同時，具有結構簡單、成本低、功耗低、易于制造等優點。該傳感器由2個單環增量式時柵傳感器構成，它們被布置為電容陣列的外圈和內圈，分別包含N和M個測量周期，N和M為互質數。周期數少的作為傳感器粗測部分，周期數多的作為傳感器精測部分，實現高精度角位移測量，利用2組傳感器輸出行波相位差和空間角度唯一對應關系實現絕對角位移測量，該絕對定位方法實現簡單，避免了復雜的編碼解碼過程。

1 傳感器測量原理

1.1 電場式時柵傳感器測量原理

傳感器由動尺和定尺2個部分組成，單圈增量電場式角位移傳感器的部分結構如圖1所示，定尺和動尺基體上的極片分別采用矩形激勵電極和雙正弦感應電極，4組激勵電極通過電極下沿4根導線連接，相鄰4個極片構成一組對極(周期)，然后依次將N個對極布置在圓的整周上，因此傳感器的單個對極的角度θ=2π/N，對傳感器激勵對極組4個極片施加相位依次相差π/2的四路正弦激勵信號UIS+=Amsinωt，UIC+=Amcosωt，UIS-=-Amsinωt，UIC-=-Amcosωt，其中，Am表示激勵信號的幅值，ω表示激勵信號的角頻率，t表示時間。

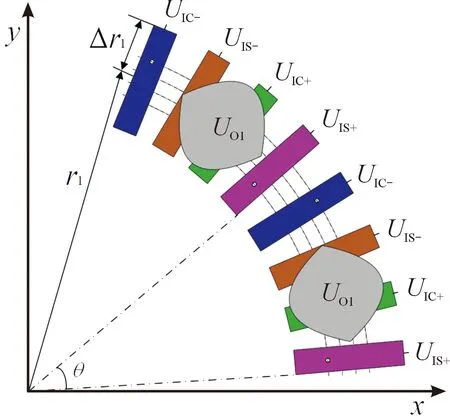
圖1 增量電場式時柵測量原理示意圖

將電極的邊緣效應忽略，激勵電極構成一個理想平板電容器，平板電容器的電容C=εS/d，其中ε是極片間介質的介電常數，S是動尺感應電極和定尺激勵電極的重疊面積，d是感應電極和激勵電極之間的間隔距離。當ε和d的值不變時，輸出信號是重疊面積S的線性響應，即當動尺相對定子轉動時，轉動的角位移值與平板電容器的有效重疊面積成正比關系。同一感應電極受到4組激勵信號傳遞的耦合信號，分別用UOS+、UOC+、UOS-、UOC-表示，只考慮IS+組形成的平面電容時，輸出信號可以表示為：

UOS+=KeΔSS+UIS+

(1)

式中：Ke是電場耦合系數，取決于間隙d；ΔSS+是有效面積的變化值。根據面積積分法，圍繞其中心旋轉任意角度θ得到ΔSS+(θ)，可以表示為：

(2)

式中：r1是感應電極在動尺上的圓周半徑；Δr1是感應電極的幅值形式。式(2)可以簡化為：

ΔSS+(θ)=2r1Δr1[1-cos(Nθ)]

θ∈[0,2π/N]

(3)

將式(3)代入式(1)，可以得到：

UOS+=2KeAr1Δr1[1-cos(Nθ)]sin(ωt)

(4)

同理，耦合信號UOC+、UOS-、UOC-也可以用上述方法得到，當傳感器處于工作狀態時，4組激勵電極同時施加四路空間相位依次相差π/2的激勵信號，將輸出信號UOS+、UOC+、UOS-和UOC-矢量疊加得到最終的感應輸出信號UO，可以表示為：

UO=UOS ++UOC ++UOS-+UOC-=

-4KeAr1Δr1sin(ωt-Nθ)=

K1sin(ωt-Nθ)

(5)

式中：K1=-4KeAr1Δr1是UO的幅值；Nθ是信號UO的相位，與傳感器的對極數N成正比變化。

由于外界電磁場會對傳感器電極的排布規律造成干擾[18]，這些干擾會導致傳感器產生非線性相位變化，從而產生較大的對極內誤差[19-20]。為了提高傳感器測量精度，提出如圖2所示的差動結構來改進傳感器傳感結構，以消除電磁場干擾導致的傳感器測量誤差。

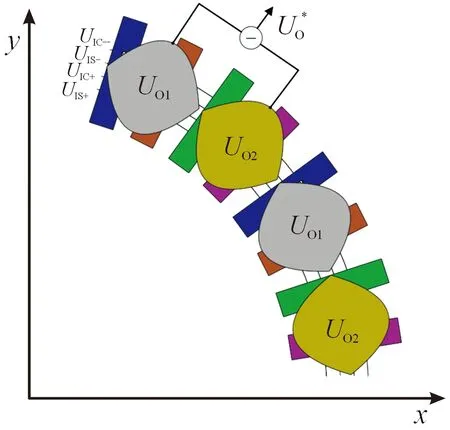
圖2 差動結構示意圖

差動結構單個對極內布置2個感應極片，且空間位置相差1/2個對極，即感應信號相位相差π，此時單個對極的2個不同的感應信號相位相反，而外界電磁場給2個感應電極帶來的干擾信號一致，在理想情況下將2個感應信號作差可以將干擾信號消除，改進后的差動傳感結構的耦合信號可表示為：

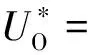
K1sin(ωt-Nθ)+

UE-[-K1sin(ωt-Nθ)+UE]=

2K1sin(ωt-Nθ)

(6)

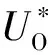
1.2 絕對式角位移測量方法

單圈式傳感器為增量式傳感器，雖然能夠實現精密測量，但采用的是增量計數方式，當傳感器啟動時，無法確定傳感器的初始位置，且傳感器突然斷電時會造成測量數據丟失，很大程度限制了其應用場景。因此，提出了一種基于傳感器外圈和內圈的對極數互質定位原理的絕對式時柵角位移傳感新方法，外圈為對極數多的N對極，采用差動傳感結構輸出耦合信號Uout；對極數少的M對極作為內圈，同樣采用差動傳感結構輸出信號Uin，傳感器結構及工作配合如圖3所示。

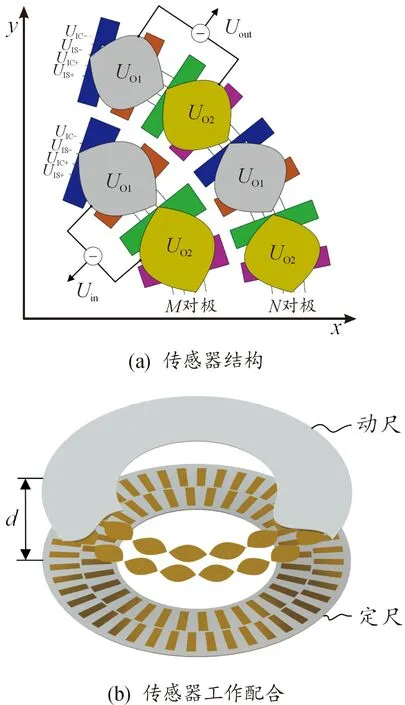
圖3 傳感器結構和工作配合示意圖

這種互質結構的傳感器誤差限Eor的表達式如下：

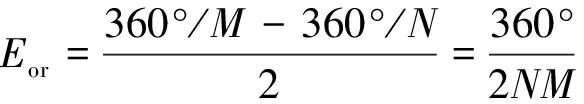
(7)

前期研究的絕對式時柵角位移傳感器采用“單對極粗測+多對極精測”和差極定位2種方案來實現絕對位置的測量。這2種方案為對極數N和M為互質數的特殊情況，其中“單對極+多對極”為1個對極和N個對極的傳感器組合；差極為N-1個對極和N個對極的傳感器組合。由于傳感器外圈和內圈在整周測量范圍內測量誤差的差值小于絕對定位誤差限時才能夠實現絕對定位，傳感器的誤差限越大，實現絕對定位的可靠性越高。由式(7)誤差限的表達式易知，當精測部分對極數N一定時，M=1 的“單對極+多對極”組合的誤差限為3種方案中最大；M=N-1 的差極組合誤差限最小。但是“單對極+多對極”的組合對單對極的測量精度要求高，不易實現絕對定位；差極組合粗測部分測量精度高但是誤差限較小，也不容易實現絕對定位。而對極數互質定位方法的絕對式傳感器與差極絕對定位方法相比誤差限更大，更容易達到絕對定位要求；且相比于“單對極+多對極”的組合方案粗測部分精度更高。因此，互質結構的絕對式角位移傳感器既能夠較容易地實現絕對定位，又能夠保證高精度。

互質結構的絕對式角位移傳感器分三步實現絕對定位，首先利用對極數為N的外圈傳感器和對極數為M的內圈傳感器之間的相位差來獲得啟動時的初始位置，然后用對極數N的外圈精測部分獲得啟動后基于初始位置的角位移變化量，最后將初始位置和基于初始位置的角位移變化量相加得到傳感器的絕對角位移。

由式(6)得出的差動信號可同理得到外圈傳感器和內圈傳感器的最終行波信號表達式為：

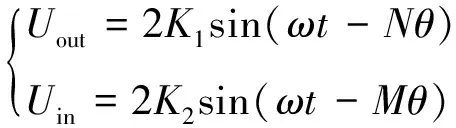
(8)

式中：K2=-4KeAr2Δr2，r2和Δr2分別為內圈感應電極在動尺上的半徑和幅值形式。通過內圈傳感器粗測和外圈傳感器精測組合測量的方式實現絕對定位功能，待測的角位移值用θa表示，外圈傳感器行波信號Uout與參考信號之間的相位差用φ1表示，內圈傳感器行波信號Uin與參考信號之間的相位差用φ2表示。φ1的值在0～2π/N周期性變化，φ2的值在0～2π/M周期性變化，φ1-φ2表示φ1和φ2之間的相位差，對于Δφ作如下定義：

(9)

傳感器絕對定位如圖4所示，相位φ1和φ2為鋸齒形，隨著其對極數呈周期性變化，Δφ在整個測量范圍內是線性變化的，具有唯一性。因此這種對極數互質的測量方法能夠實現絕對定位功能。

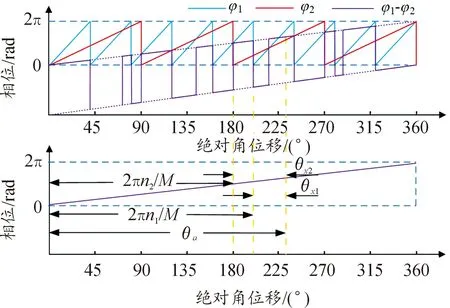
圖4 傳感器絕對定位原理示意圖

傳感器工作時，絕對角位移θa在外圈和內圈傳感器所包含的最大整數周期數n1和n2可以通過取整函數表示如下：

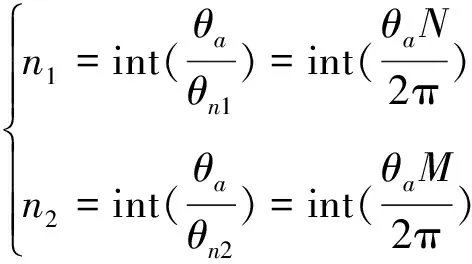
(10)

式中：θn1和θn2為外圈傳感器和內圈傳感器單對極的角位移值，則角位移值θa可以表示為：

θa=n1θn1+θx1=n2θn2+θx2=

(11)

式中：θx1和θx2為θa在外圈傳感器和內圈傳感器除了最大整數周期外的剩余角位移值。在實際測量中，盡量采用高分辨率的傳感器作為精測來提高測量精度，角位移值θa可以直接表示為：

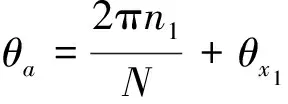
(12)

式中：θx1是精測分量；2πn1/N是粗測分量，兩測量分量相加可以得到絕對角位移θa。

2 實驗驗證

為了有效驗證這種對極數互質的絕對式角位移傳感器的性能，在恒溫恒濕的超潔凈實驗室進行實驗驗證，實驗平臺裝置如圖5所示，為了減小振動對實驗結果的影響，將RPI精密氣浮轉臺安裝在經過防震處理過的大理石平臺上，利用配套的RPI轉臺控制系統控制轉臺轉動，轉臺內部采用海德漢RON 905光柵作位置反饋，在整周范圍內該測試系統精度能夠達到±0.5″。

圖5 實驗平臺裝置

傳感器樣機采用印制電路板(PCB)制造工藝制作，主要參數為外徑154 mm、內徑100 mm、厚度2 mm，傳感器樣機的外圈為精測部分，對極數N設計成180對極，內圈為粗測部分，對極數M設計成119對極。在保持恒溫濕度的環境搭建好測試平臺，定尺和轉尺安裝在大理石基座上，定尺和動尺安裝間隙為0.6 mm，通過反復調整保證定尺、轉尺、氣浮旋轉臺同軸安裝，減少安裝帶來的測量誤差。信號處理系統采用FPGA芯片生成相位相差π/2的四路標準正弦交流激勵信號和一路參考信號，將激勵信號產生電路和耦合信號處理電路集成到信號處理系統中，通過耦合信號處理電路完成行波信號拾取、濾波、放大和整形處理后送入到FPGA，經過計算得到含有絕對位置信息的絕對角位移值。

3 實驗結果和誤差分析

傳感器樣機內外圈有同樣的測量誤差機制，傳感器樣機的精度取決于精測部分的測量誤差。傳感器外圈單個對極量程為2°，內圈單個對極量程約為3°，將動定子安裝間隙調整為0.6 mm，在沒有補償的情況下以步長增量為0.1°和0.15°控制轉臺分別對傳感器樣機進行靜態采樣，每個對極的數據樣本為20個點，對采樣點數據與轉臺內部光柵測得的數據作差，得到對極內測量誤差，并對結果進行頻譜分析，得到結果如圖6所示，外圈和內圈的對極內測量誤差的峰峰值分別為3.2″和4.2″，且外圈和內圈的對極內誤差規律基本相同，經過傅里葉頻譜分析，誤差成分包含一次、二次、四次諧波誤差，主要由四次諧波誤差組成。

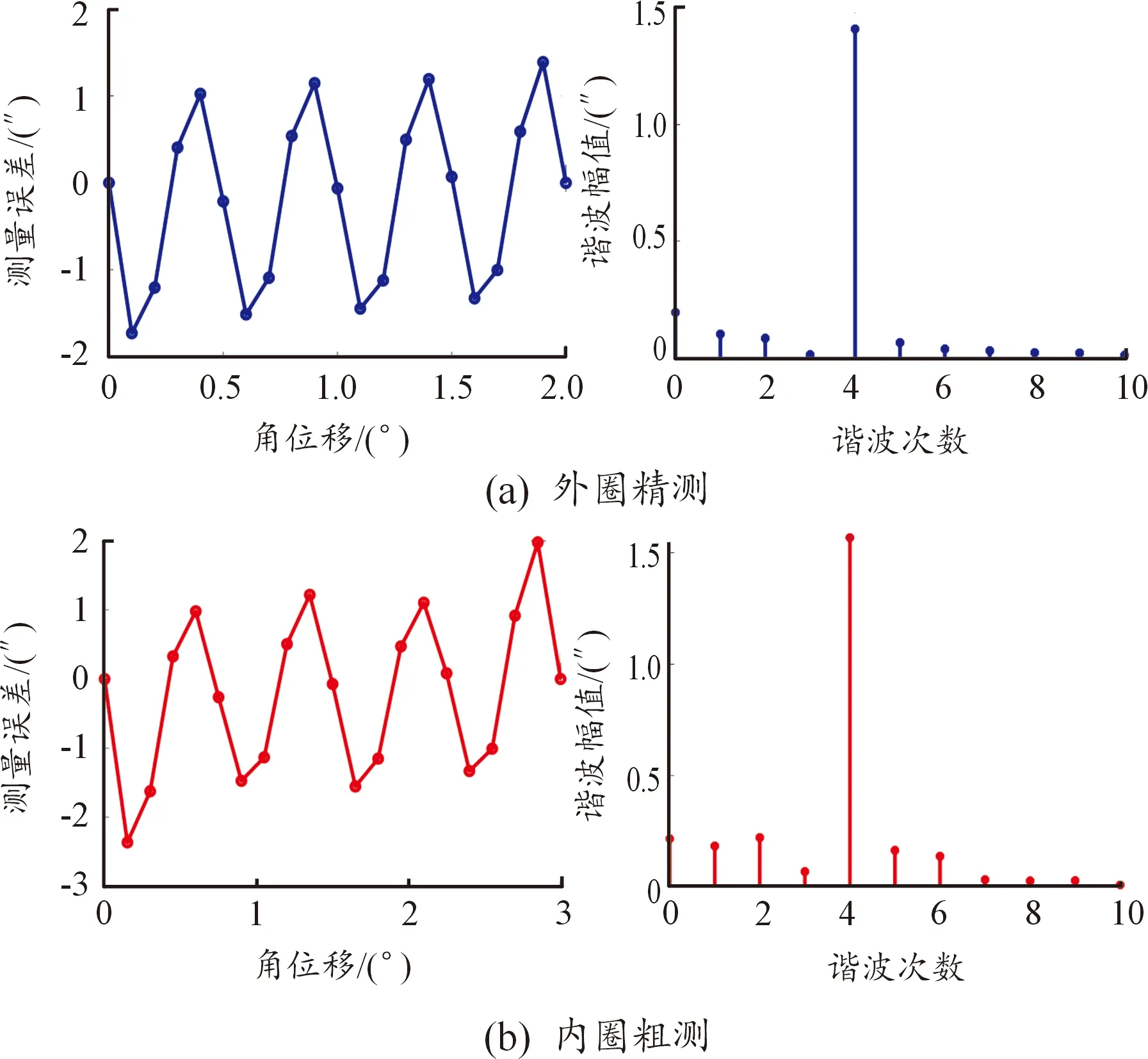
圖6 傳感器樣機對極內誤差曲線

導致四次諧波誤差產生的原因是電場的非線性分布和平板電容邊緣效應的影響。由于電場式時柵傳感器屬于電容式傳感器，電容式傳感器的電容極板之間存在靜電場，使得電容極板邊緣處的電場分布不均勻，傳感器一個對極由4個平板電容極片組成，受邊緣效應的影響，一個對極會存在4個電場分布不均勻的區域，從而引入對極內的四次諧波誤差[16,20]。

在同等條件下以步長增量0.9°控制轉臺對傳感器樣機進行靜態采樣，測量傳感器樣機外圈和內圈的整周誤差，測量誤差曲線如圖7所示。

傳感器樣機外圈和內圈的整周測量誤差的峰峰值分別為3.6″和4.5″，并且整周誤差除了存在安裝導致的少量一次誤差外基本都是對極內的4次誤差。根據式(6)可計算得出該絕對式傳感器樣機的誤差限Eor=360°/(2*180*119) ≈30.25″。測量結果遠遠小于傳感器的誤差限，能夠實現絕對定位，且傳感器樣機在整周360°沒有補償的情況下絕對式角位移測量誤差為±1.8″。

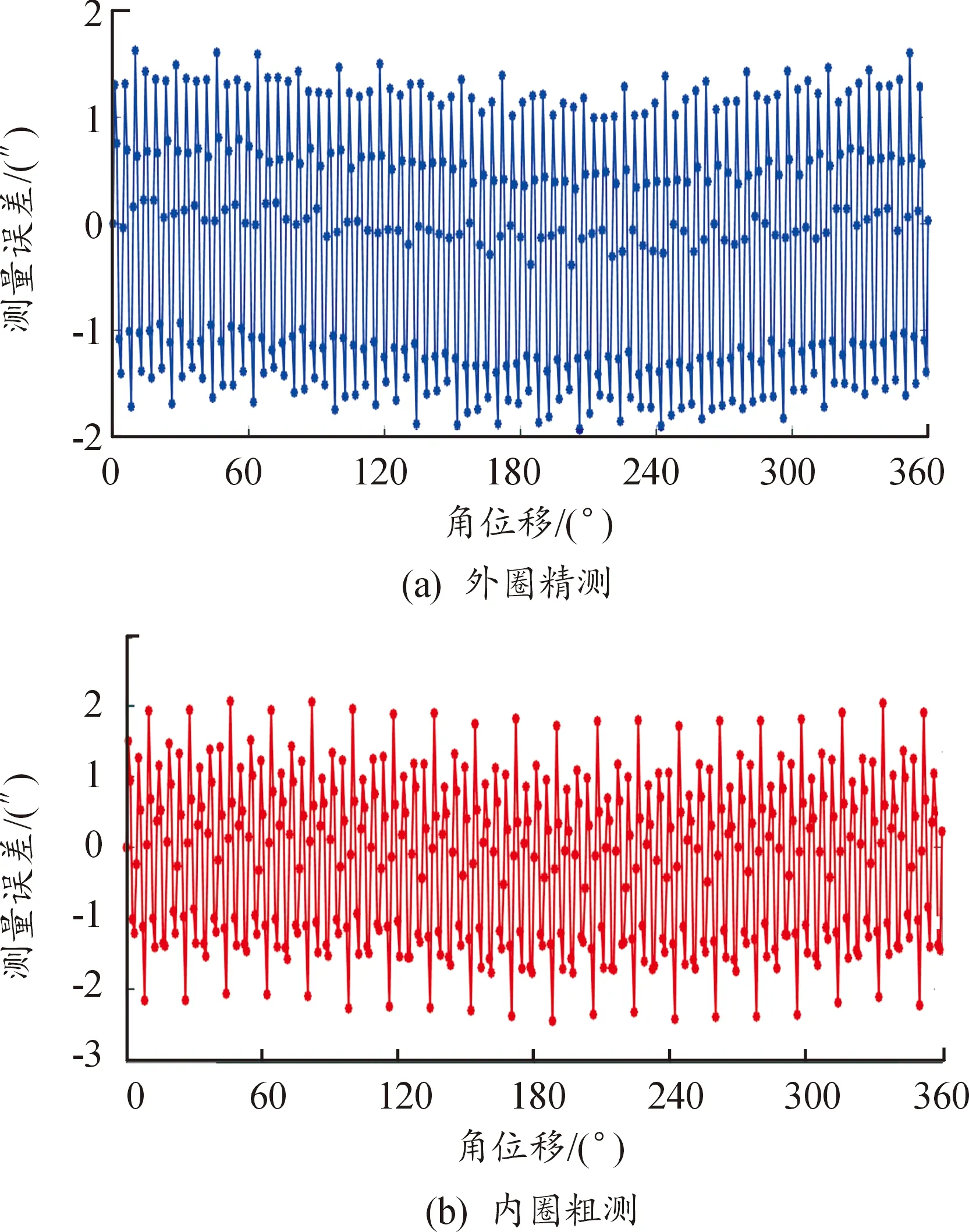
圖7 傳感器樣機整周誤差曲線

4 結論

提出了一種對極數互質的高精度絕對式時柵角位移傳感器，將2個不同周期的增量式傳感器組合測量實現傳感器的絕對定位功能，在傳感器設計階段采用差動結構消除共模干擾，并且使傳感器信號強度翻倍。通過PCB工藝制造了外徑 154 mm、內徑100 mm、厚度2 mm的傳感器樣機，對傳感器樣機進行測試，測得傳感器在整周360°沒有補償的情況下測量精度為±1.8″，實現了高精度角位移測量。在接下來的工作中，將對對極內殘留的四次諧波誤差進行詳細分析，進一步提高精細測量分量的原始測量精度。