協作機器人參數辨識與誤差補償算法研究

秦 蒙，陳良培，孟琨泰

(1.重慶電力高等專科學校 信息工程學院， 重慶 400053；2.中國科學院深圳先進技術研究院 光電工程技術中心， 廣東 深圳 518055；3.河北機電職業技術學院， 河北 邢臺 054000)

0 引言

隨著市場經濟的快速發展，個性化定制的市場體量正在日益擴大，實體工業生產模式正在從大批量、單一化的剛性生產線向著小批量、多樣化、定制化的柔性生產線轉變。工業企業對機器人的需求不再局限于單一重復性的作業，而是希望機器人能夠在多元化工作場景中像人一樣快速轉換完成各類復雜任務。因此協作機器人應運而生，它可以在指定協作區域內與人進行交互作業，具有安全性高、通用性好、易于編程使用的特點[1-2]。

目前市場上的協作機器人的構型大多采用7自由度的串聯式冗余機械臂構型。串聯構型的7R協作機器人長懸臂、大負載的限制，使得機器人剛柔耦合變形誤差較大[3-5]。另外，考慮制造誤差、加工誤差、控制器控制誤差以及溫度場等外界使用環境的影響使得冗余構型的協作機器人末端執行器的位置誤差較大，絕對定位精度較低，嚴重影響了協作機器人的高精度定位作業和人機協作、人機共融的發展。

協作機器人作為典型的多輸入多輸出的非線性時變動力學系統，在工作過程中往往要承受非線性摩擦、可變載荷、外界未知干擾、多物理場等的動態干擾。針對協作機器人串聯多關節的結構特點，傳統的控制策略主要有自適應控制、神經網絡控制、滑模控制(SMC)和變結構控制等[6-10]。其中滑模變結構控制因具有較強的魯棒性和對非線性、不確定動態和有界輸入擾動不敏感的特點，被廣泛應用于非線性系統的逼近。Yen等[11]研究了柔性機械臂在未知擾動下的期望軌跡跟蹤的非線性控制算法，基于歐拉-拉格朗日法推導了機械手的動力學方程，設計了非線性控制律[12]。Soltanpour等[13]提出了一種簡單的模糊滑模控制方法來實現對機械手的軌跡跟蹤。

考慮協作機器人剛柔耦合使得末端執行器產生較大的絕對位值誤差，單純的設計控制器將無法實現高精度軌跡跟蹤，必須對其進行非線性系統辨識[14-17]。目前，多場耦合柔性體系統往往呈現高度非線性、強耦合的動力學特性，且某些耦合因素對動力學行為的影響并不明朗，導致動力學模型存在未知部分，加深了協作機器人動力學系統的非線性，影響末端絕對位置精度。針對機器人位置精度提高的方法有2種：誤差預防法和誤差補償法[16]。誤差補償法相比于誤差預防法，成本低且補償效果明顯，是降低機器人位置誤差的重要途徑。常用的誤差補償方法有運動學標定和非運動學標定。運動學標定主要解決的是運動學建模時DH參數誤差(幾何誤差)，非運動學標定主要解決機器人的非幾何誤差，包括機器人桿件和關節的柔性變形、末端可變負載、溫度場等外力場引起的變形、變速齒輪的傳動誤差等。對于協作機器人大負載搬運應用領域，非幾何因素是影響機器人軌跡和定位精度的主導因素之一，因此進行協作機器人非幾何誤差的辨識極具實際應用意義。

針對機器人系統參數誤差辨識的問題，Gao等[18-19]基于BP神經網絡改進的粒子群優化算法進行工業機器人的參數辨識。Nubiola等[20]考慮所有可能的幾何誤差和位姿參數，采用最小二乘技術和大量實驗優化了ABB 1600型機器人末端位置誤差。 Madsen等[21]將已知的逆動力學辨識模型與剛性機器人非線性動力學的加權最小二乘模型相結合，通過降低建模誤差來提高標定精度，有效補償了轉子慣性力矩和非線性摩擦力。Qiao等[22]采用基于指數公式乘積的標定方法，通過伴隨變換來表示2個扭轉之間的變換關系，僅依賴于參考構型，通過一次標定即可獲得機器人的精確運動參數；王一等[23]通過建立柔性關節的彈性扭簧模型，將柔度誤差分解為外加負載柔度誤差和機械臂自重柔度誤差分別進行補償。

剛柔耦合狀態下的柔性關節、柔性桿的變形誤差、控制器控制誤差、末端變載荷變空間位姿下的變誤差的影響使得協作機器人末端執行器的軌跡跟蹤誤差較大。為了解決這些問題，以庫卡LBR協作機器人為例進行分析，基于網格化工作空間原理和線性化可變負載模型對協作機器人進行變參數誤差補償，基于有限元軟件建立協作機器人剛柔耦合模型，并利用ADAMS-Matlab/Simulink聯合進行協作機器人誤差分析與變參數補償算法驗證，提高末端執行器軌跡跟蹤精度。

1 協作機器人運動學與動力學分析

1.1 運動學建模

協作機器人正向運動學模型是進行絕對位置誤差標定的基礎。為了直觀地表述協作機器人關節空間位置，將各關節的坐標系建立在對應的關節軸上，如圖1所示。

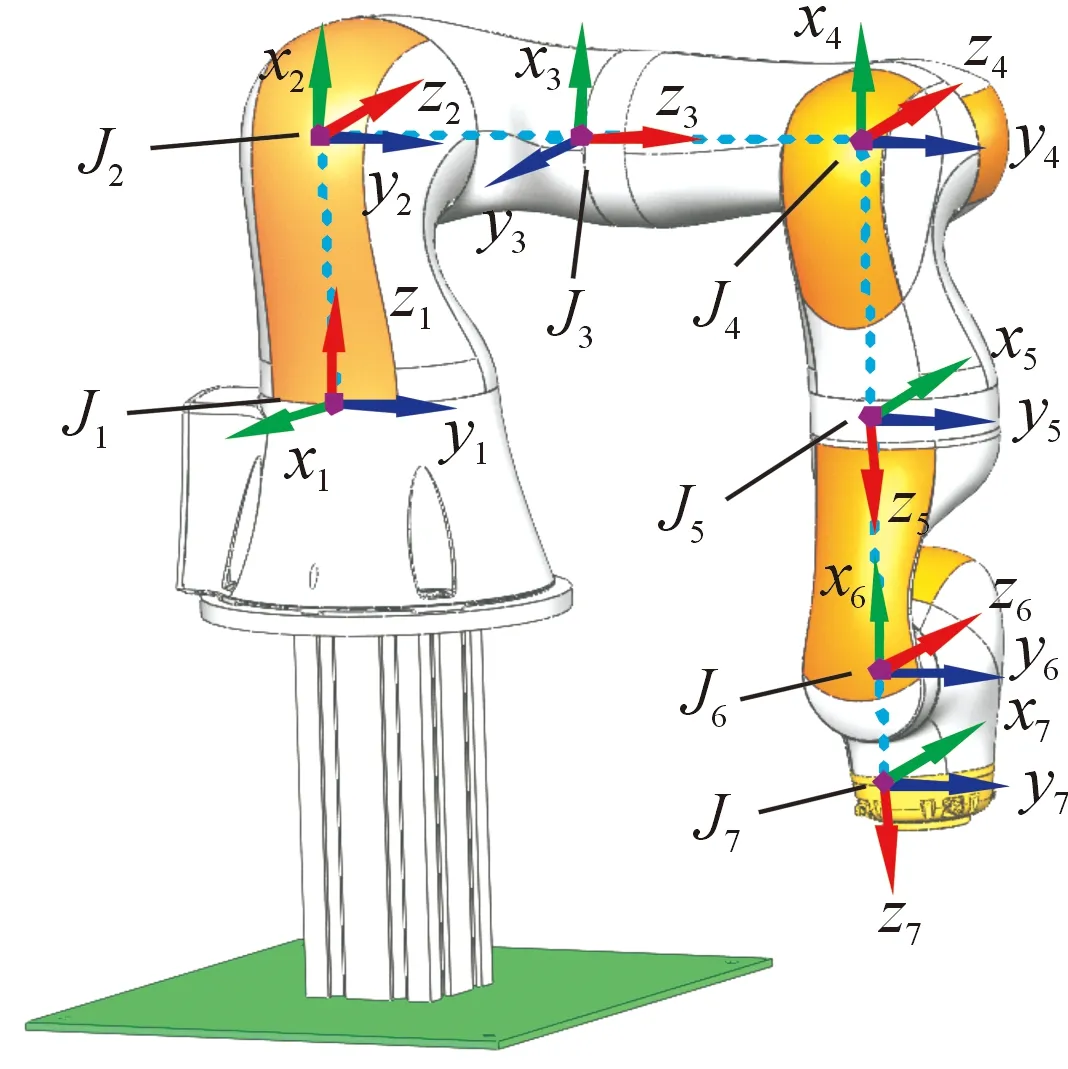
圖1 庫卡LBR協作機器人坐標系示意圖

正向運動學建模方法采用改進后的DH模型建立，具體參數如表1所示，相鄰兩連桿之間的齊次坐標變換矩陣為：

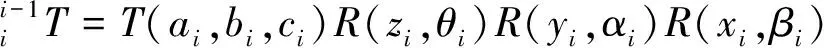
(1)

式中:ai,bi,ci為連桿偏距;θi,αi,βi為關節轉角共同組成改進后的DH參數。

則協作機器人末端負載相對于基坐標系的位置關系可以表示為：

(2)

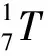
表1 LBR協作機器人改進的DH參數

1.2 動力學建模

通過拉格朗日方程建立機器人剛柔耦合動力學方程。庫卡LBR協作機器人是典型的串行多關節機械臂，最終動力學模型表示為：

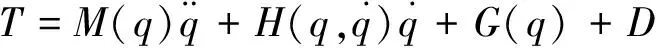
(3)

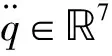
用拉格朗日方程展開式(3)可得任意關節p的扭矩為：

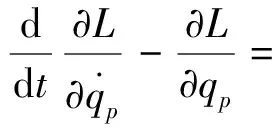
(4)

式中：L=K-P為拉格朗日函數，表示蛇機器人動能K與勢能P之差；Ii為偽慣量矩陣；mp為連桿質量;mgp為負載質量。

2 協作機器人控制系統建立

進行協作機器人參數辨識不但需要考慮幾何和非幾何參數的影響，控制誤差也是不可忽略的因素之一。協作機器人的控制目標是設計一個穩定的控制器，使各關節輸出軌跡q快速準確地跟蹤期望軌跡qd，即保證跟蹤誤差e在有限時間內收斂到零。基于1.2節協作機器人動力學方程的特點，設計了一種基于RBF神經網絡的滑模自適應控制器(RSMC)，原理如圖2所示。

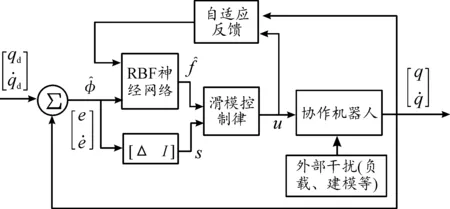
圖2 神經網絡滑模自適應控制原理示意圖

對協作機器人動力學方程式(3)進行滑模控制器設計，假設理想角度為qd，誤差為e(t)=q-qd，則可設計滑模控制律為：

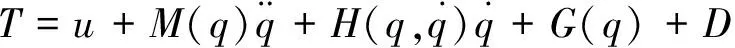
(5)

式中:u為反饋控制律。將式(5)代入式(3)可得到：

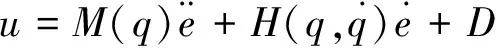
(6)

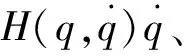
針對以上特點，并結合神經網絡的萬能逼近特性，可以逼近外界干擾及不確定性，并加以補償。因此可采用RBF神經網絡與滑模控制結合實現上述不確定性系統的控制。

神經網絡由于其固有的逼近能力，被廣泛用于逼近未知非線性曲線[24]。用RBF網絡逼近一個連續函數Vi(X)∶Rq→Rp可以表示為：

Vi(X)p×1=WTh(Xin)+ε(Xin)

(7)

式中：Xin=[x1,…xn]是網絡輸入；W∈Rp×q是網絡權值；n>1,是神經元數量；[h1(Xin)…hq(Xin)]T∈Rq為高斯基函數；ε(Xin)為網絡逼近誤差。

高斯RBF神經網絡基函數h1(Xin)網絡算法為：

i=1,2,…，n

(8)

式中：Ci,bi為第i個神經元的中心和寬度。

(9)

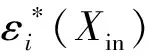
3 參數辨識及誤差補償算法

3.1 矩陣微分法誤差建模

機器人在關節空間內的參數誤差因連桿柔性、關節柔性、自重、負載和電機控制等因素的影響，呈現出不均勻分布的特點。對于協作機器人，由于各關節參數存在誤差，根據微分變換法對相鄰連桿間的坐標變換進行全微分可得：

(10)

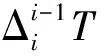
由于關節參數存在誤差，末端坐標系相對于基坐標系的齊次變換矩陣為：

(11)

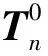
(12)

可得協作機器人末端位置偏差ΔP為：

ΔP=PR-PN=BΔη

(13)

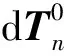
為求解式(13)中的參數誤差值，需要引入多個采樣點：

(14)

式中，n為采樣的個數。

協作機器人在關節空間內的參數誤差因連桿的柔度、關節的柔度、控制器控制誤差、自重、負載的變化而變化。隨著協作機器人關節空間內轉角的變化，關節轉角會產生一定誤差，但同時伴隨著連桿柔度誤差、控制器控制誤差，其他參數也會產生一定程度的變化[26]。因此，協作機器人的各個參數誤差均可以表示成關于關節空間內關節角的函數：

Δη=(Δθ,Δα,Δa,Δd)=f(θ1…θ7)

(15)

式中：Δη表示參數誤差的集合。因為協作機器人各關節轉角θ1…θ7相互耦合，難以建立關節空間內的誤差模型，因此可以將協作機器人關節空間內的確定空間位姿轉換到工作空間進行求解：

f(θ1…θ7)=g(x,y,z)

(16)

3.2 工作空間變參數誤差補償

由式(15)、(16)可知，給定關節空間或者工作空間內的一組位姿參數就可以確定該位姿下的協作機器人參數誤差Δη。協作機器人末端執行器在工作空間中的位姿變化較大，各個空間位姿下的連桿柔度、關節柔度、控制器控制誤差、自重等非幾何因素造成末端執行器位置誤差分布不均。另外，協作機器人末端承受十幾千克可變負載，對末端執行器的位置精度也具有較大影響。因此，采用單一的固定參數誤差集合Δη補償整個工作空間內的位置誤差時，協作機器人末端執行器的絕對位置精度提升有限。

采用對協作機器人工作空間進行網格化的變參數誤差補償方法，如圖3所示。對工作空間進行網格劃分，依次辨識各個網格內的參數誤差Δηi，從而提高協作機器人末端執行器在整個工作空間內的絕對定位精度。針對協作機器人工作空間內的單個網格，如圖 3所示，末端負載恒定時，協作機器人所受連桿柔度、關節柔度、控制器控制誤差、自重等非幾何因素影響非常接近，因此在小范圍內犧牲一定程度位置精度的前提下，可采用單一參數誤差集合Δηi進行誤差補償。當負載變化時，在單個網格內協作機器人可以簡化為線彈性懸臂梁結構(忽略隨機誤差的影響)，因此其末端的位置誤差可以等效為：

Δx=kamg+Δx0

(17)

式中：Δx為空間位置誤差；ka為位置誤差系數；Δx0為零負載下的位置誤差。

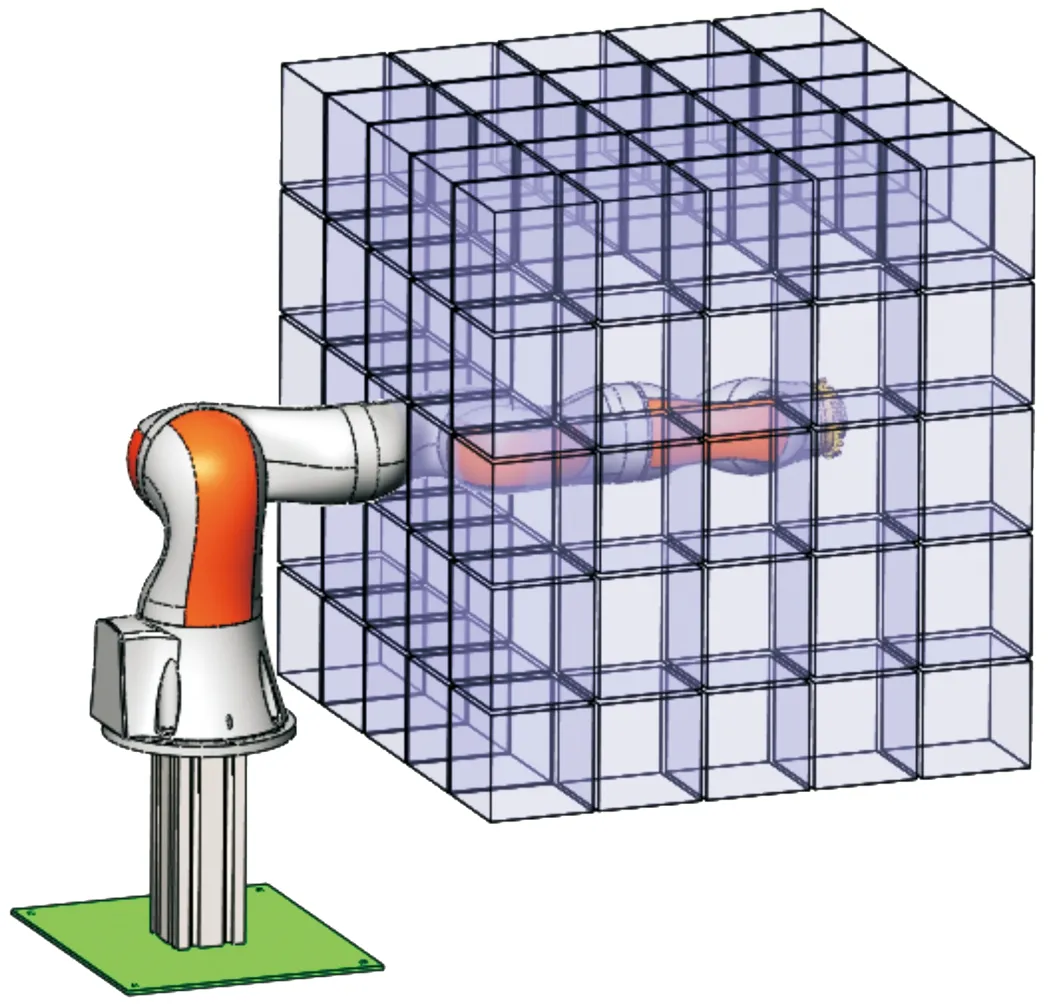
圖3 工作空間網格化原理示意圖

同理，可以得到關節空間內變負載下的一組參數誤差矩陣為：

(18)

根據上述分析可知，單個網格劃分得越小，協作機器人所受連桿柔度、關節柔度、控制器控制誤差、自重等非幾何因素影響越接近，單個網格內的協作機器人線彈性懸臂梁結構相似度越高，從而末端執行器在整個工作空間內的絕對定位精度越高。

3.3 參數誤差求解流程

采用非線性阻尼最小二乘算法中的Levenberg-Marquardt (LM)算法進行協作機器人參數誤差求解。LM 算法是使用最廣泛的一種優化算法，其最終目標是尋找一組使函數具有最小值的參數向量，是利用梯度來求極值的算法。相較于高斯牛頓法與梯度下降法，LM算法既有梯度下降法的全局搜索、快速尋優的能力，也具有高斯牛頓法的快速收斂到最優解的能力，在處理冗余參數問題時具有獨特的優勢，在參數求解時能有效避免陷入局部最優，處理復雜問題的效率也較高。

高斯牛頓法的迭代式為：

xk+1=xk+hgn

(19)

xk+1=xk+H-1▽f

(20)

(21)

式中：▽f為雅可比矩陣;H為海塞矩陣。因此：

(22)

Levenberg-Marquardt算法是對高斯牛頓的改進，在迭代步長上略有不同：

(23)

根據機器人具體結構和理論結構參數對雅克比矩陣及其他參數進行初始化，ε>0，α1>m>0，0≤p0≤p1≤p2≤1，k=1。LM算法的每次迭代主要包括5部分：

步驟1建立目標函數，根據式(39)可得ΔP=PR-PN=BΔη，式中ΔP為末端空間位置偏差；Δη為待求的參數誤差向量；

步驟2 根據機器人具體結構和理論結構參數對雅克比矩陣及其他參數進行初始化，確定尋優初始值Δη，終止控制常數ε≥0，并根據初值Δη計算第k次迭代時的當前空間位置誤差ΔP；

步驟3根據第k次估計值計算第k次迭代時雅可比矩陣J(xk)；并利用阻尼最小二乘法求解參數誤差矩陣：

Δxk=-(JT(xk)J(xk)+λkI)-1JT(xk)ΔP(xk)

(24)

式中：k表示迭代次數；Δxk表示第k次迭代時的參數誤差改變值；xk表示第k次迭代的參數誤差；λk表示第k次迭代時的阻尼因子。

(25)

計算更新參數誤差矩陣后第k+1次迭代時的機器人當前空間位置誤差:

ΔP(xk-Δxk)=PR-PN(xk-Δxk)

(26)

計算第k次迭代時實際下降量ΔFk與預估下降量ΔLk的比值qk:

(27)

(28)

定義實際下降量ΔFk和預估下降量ΔLk的比值qk來監控步長的質量：

(29)

步驟4更新迭代參數。

預估下降量ΔLk>0是人為構造，因此，若qk很小或者為負值，說明迭代失效，此時xk+Δxk不能作為下一個迭代點，須增大阻尼因子λk、減小步長xk-Δxk，進行重新求解以便下次迭代時更接近于梯度下降法。實現全局搜索；若qk很大，此時迭代有效，可以減小阻尼因子λk，增大步長xk-Δxk，以便下次迭代時算法更接近高斯牛頓算法，實現快速收斂到最優解，其他情況下阻尼因子λk與迭代步長不變。由此可得第k次迭代參數更新法則。

第k+1次參數誤差矩陣更新法則：

(30)

第k+1次阻尼因子更新法則：

(31)

k=k+1

(32)

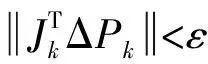
4 仿真驗證

為了驗證RSMC控制器對協作機器人剛柔耦合模型軌跡跟蹤精度，以及LM變參數誤差補償算法的效果，在Matlab/Simulink環境下對RSMC控制器進行建模，并結合ADAMS動力學分析軟件建立協作機器人三維動力學模型，利用ANASYS軟件有限元軟件對協作機器人剛性連桿進行柔性化處理實現剛柔耦合聯合仿真。協作機器人基座連桿變形較小，剩余連桿為鋁合金材料變形較大，設定第一關節后的鋁合金連桿彈性模量70 GPa，泊松比為0.3，進行柔性化處理，可得如圖4所示機電一體化仿真模型結構。剛柔耦合的變形結果如圖5所示。

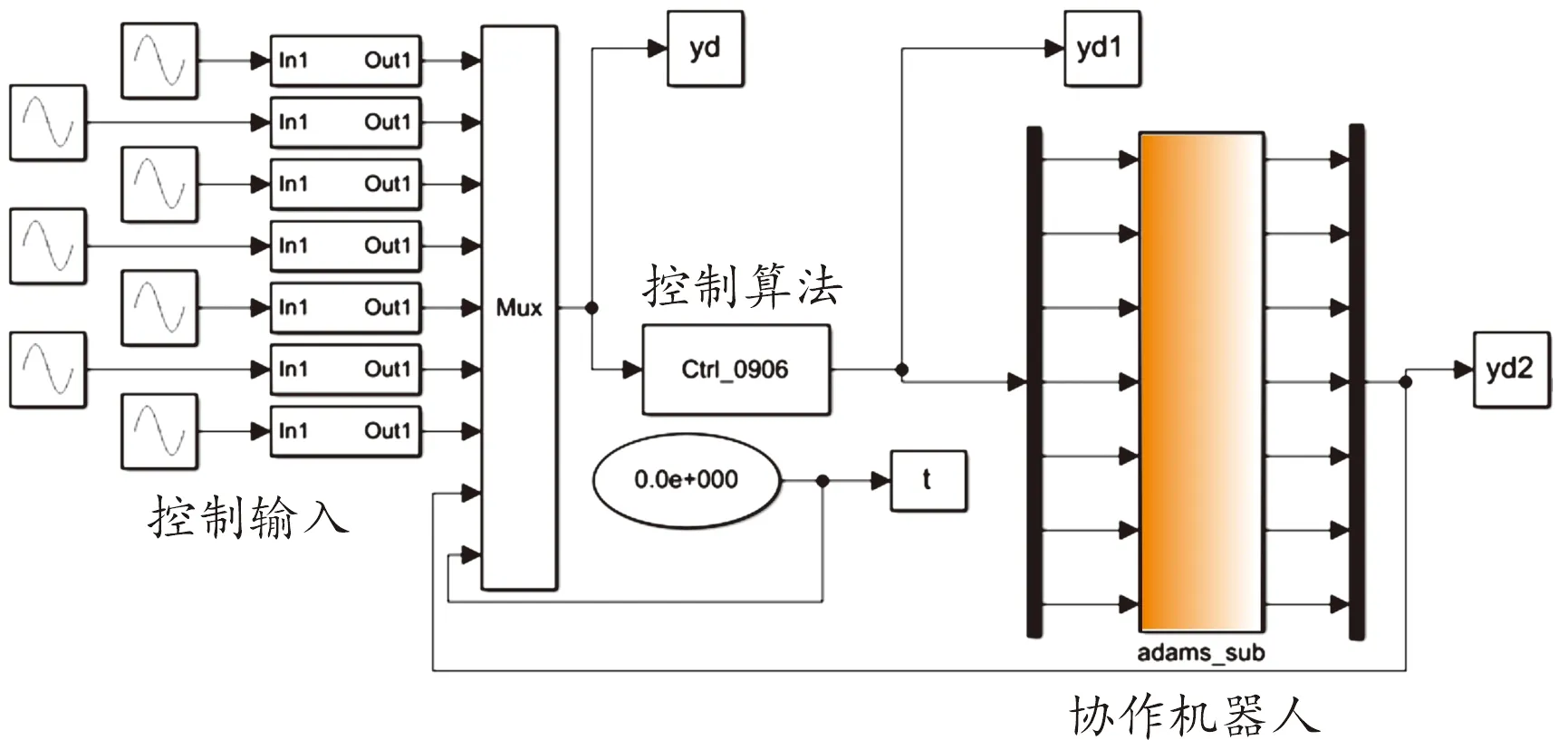
圖4 協作機器人機電一體化仿真模型結構

圖5 剛柔耦合的變形結果

4.1 RSMC控制器控制效果

給定關節2正弦曲線控制信號如圖 6(a)，設定末端執行器不同負載(0～6 kg)進行RSMC控制器控制性能仿真，仿真時序如圖5所示，結果如圖6所示。分析結果可得：仿真過程中關節扭矩輸出平穩，僅起始階段存在阻尼振蕩；極限工況下關節角位移最大跟蹤誤差約為0.008 rad，平均角位移誤差約為0.000 1 rad，末端執行器沿Z軸最大位置誤差約為7 mm，平均位置誤差約為 4.7 mm，主要來自于協作機器人柔性連桿自重和末端負載引起的沿Z軸的位置誤差。總的來說，設計的RSMC控制器性能較好，位置誤差較小。

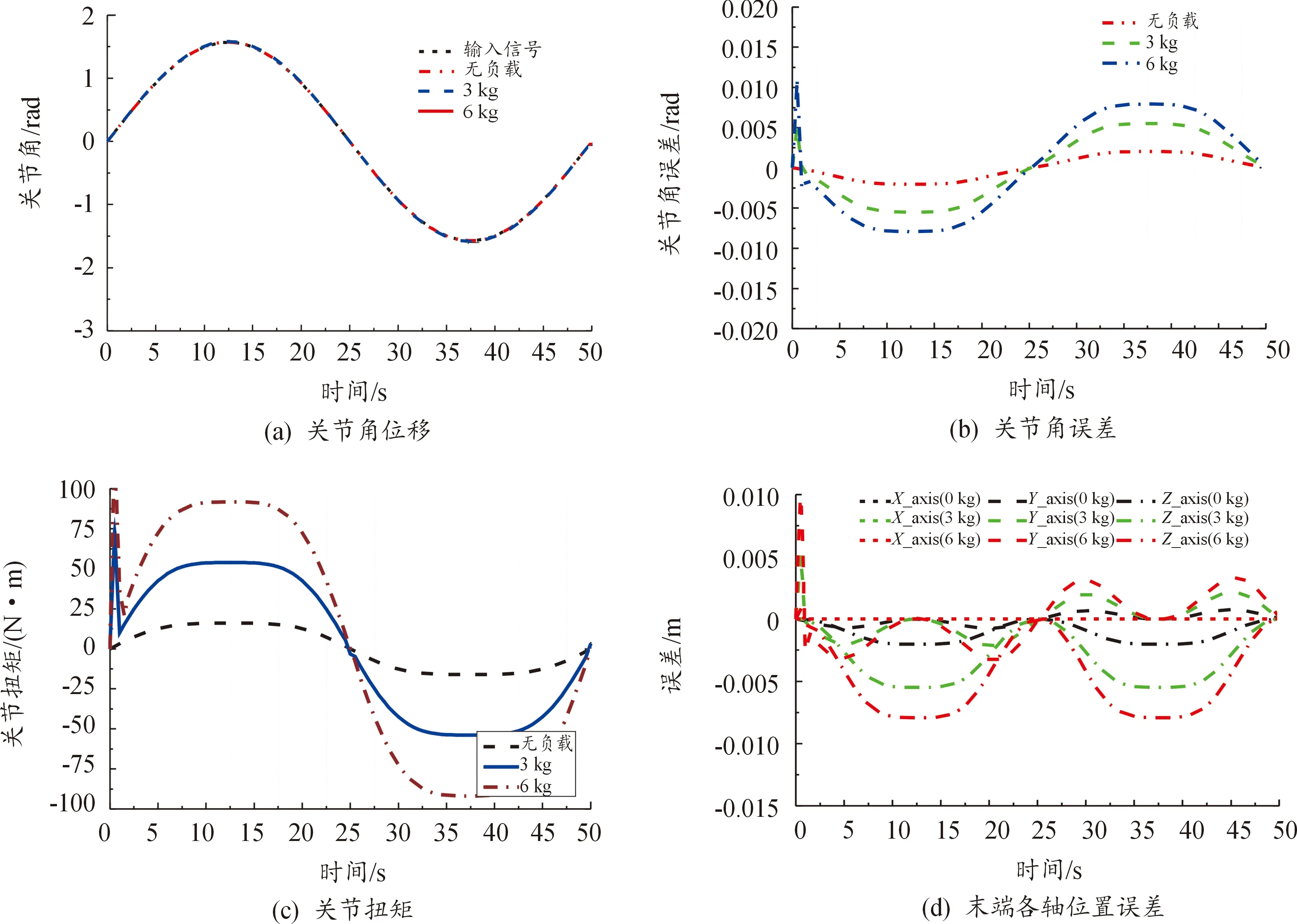
圖6 基于RSMC控制器協作機器人剛柔耦合仿真結果

4.2 LM算法位置誤差補償修正

將協作機器人工作空間沿基坐標系Y軸均勻分成1、4和8份，分別利用LM算法、網格化工作空間和線性化可變負載模型進行變參數誤差補償。不同末端負載下(0～6 kg)各網格化的工作空間內補償參數如表2、3所示，將補償參數代入RSMC控制器重新仿真，結果如圖7—9所示。負載越大，關節角誤差、末端位置誤差越大。補償后協作機器人極限工況下關節角平均誤差小于0.002 rad，沿Z末端平均位置誤差小于0.2 mm，大大降低了末端位置誤差補償，效果明顯。圖7—9中，在起始、終止以及中間時刻(25 s)的位置誤差較大，主要是該區域誤差值的變化范圍較大、網格化工作空間較為稀疏導致，可進一步細化網格以提高位置精度。

4.3 線性化變負載補償

將同一空間網格下不同負載的參數誤差補償值繪制成曲線圖，如圖10所示，發現同一空間網格不同負載下的參數誤差補償值與負載成線性關系。通過計算斜率即可得到各種負載質量下的位值誤差補償值。

表2 工作空間4網格位置下的補償值 rad

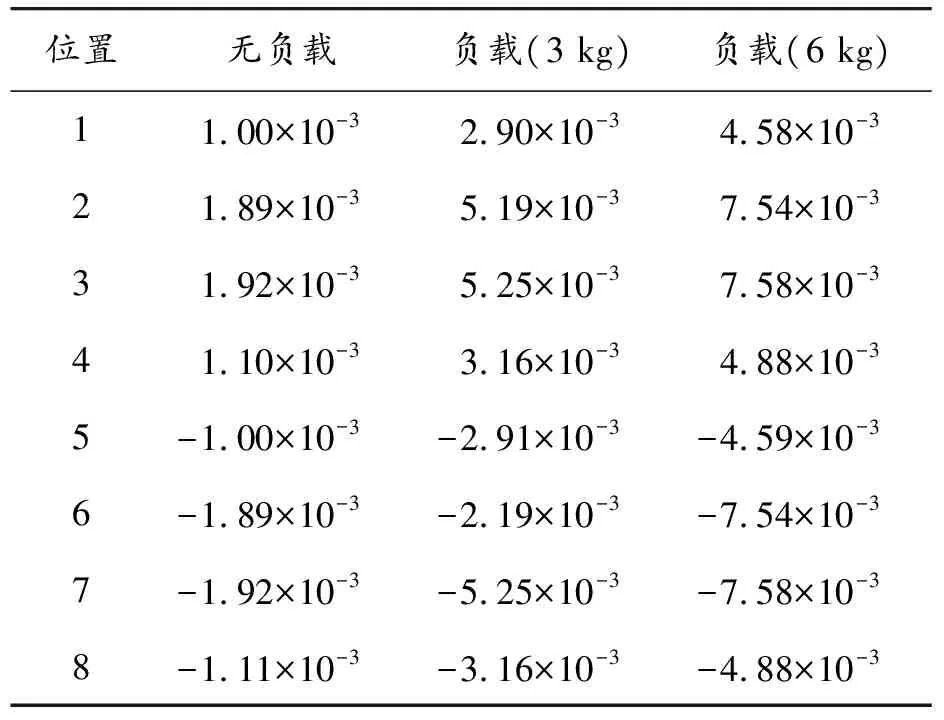
表3 工作空間8網格位置下的補償值 rad

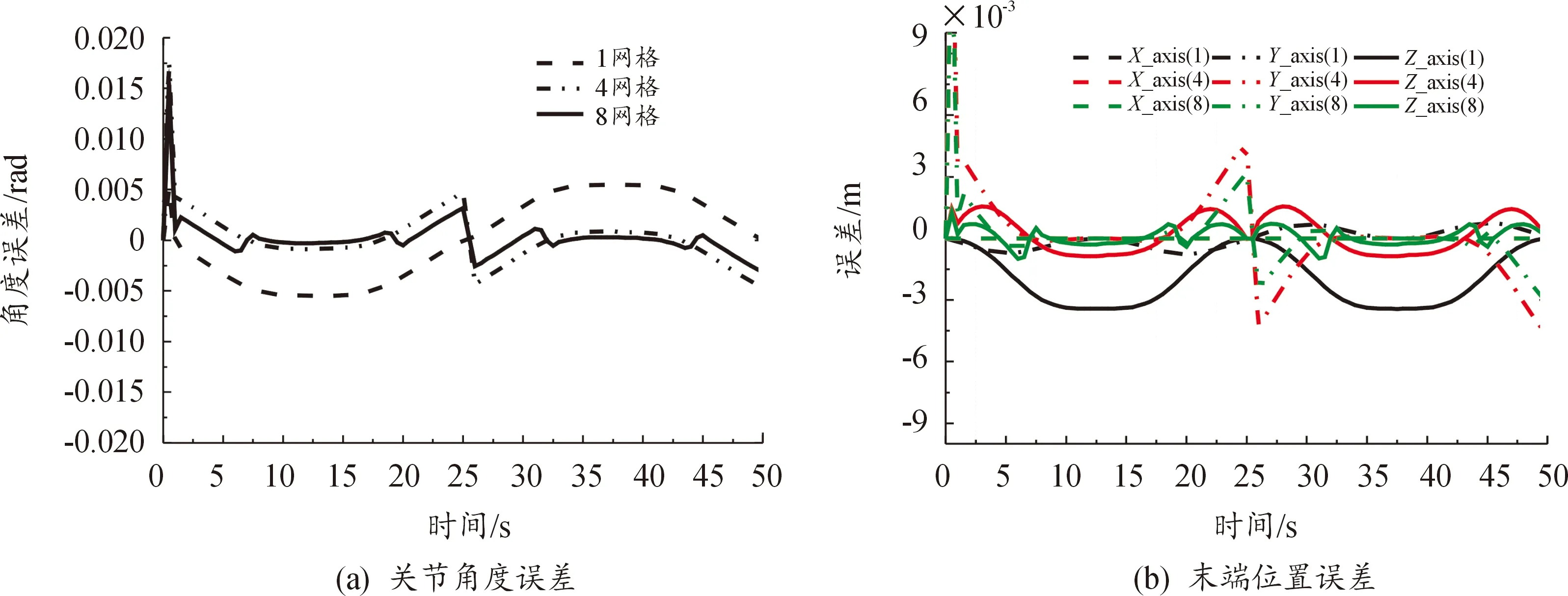
圖8 協作機器人3 kg負載變參數誤差補償結果

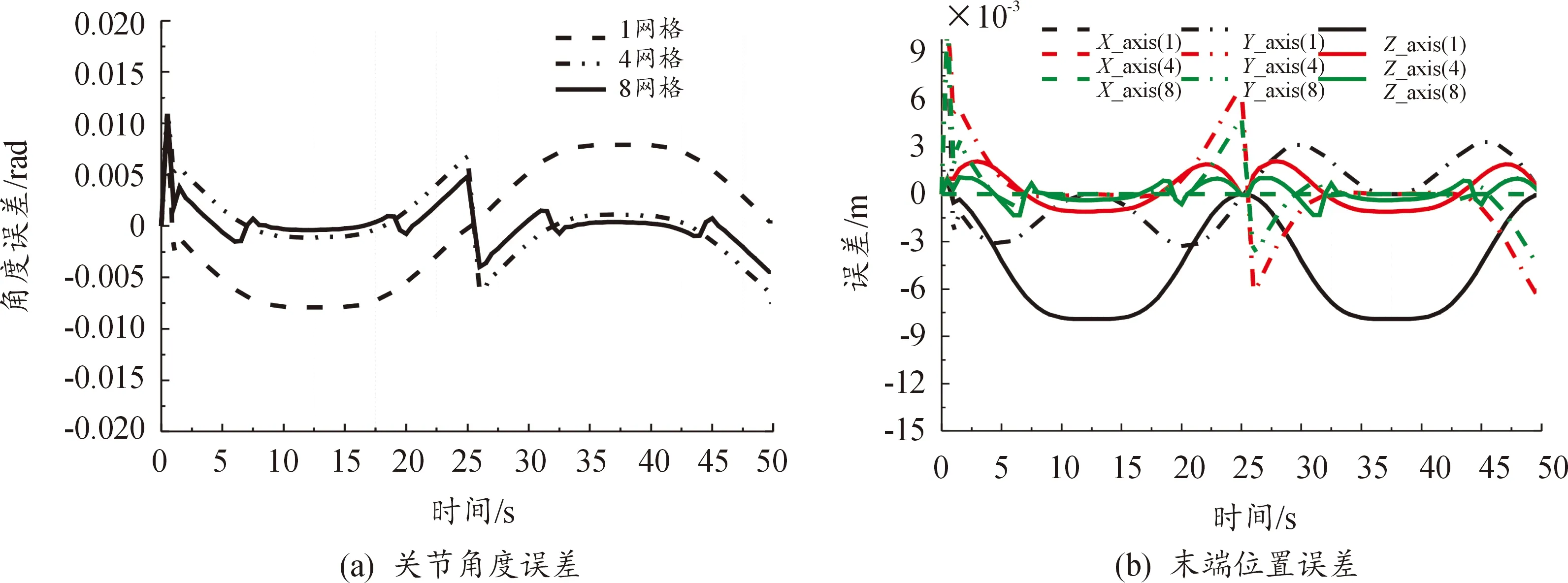
圖9 協作機器人6 kg負載變參數誤差補償結果

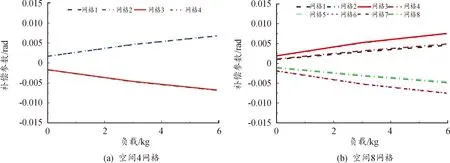
圖10 線性化可變負載補償

5 結論

基于協作機器人剛柔耦合動力學模型，設計了一種基于RBF神經網絡的滑模自適應控制器。通過ADAMS-Matlab/Simulink聯合仿真驗證了控制器的效果。分析了協作機器人剛柔耦合模型極限位姿下的軌跡跟蹤誤差。結果表明：極限位姿下協作機器人剛柔耦合模型末端執行器位置誤差極值約為7 mm，平均誤差約為4.7 mm。其誤差來源主要是控制誤差、懸臂狀態下沿Z軸負載及自重造成的協作機器人桿件變形誤差。為了補償位置誤差，基于L-M非線性阻尼最小二乘法，結合空間網格和線性化可變負載模型推導了協作機器人工作空間變參數誤差補償算法。通過聯合仿真驗證了軌跡跟蹤誤差補償效果，結果表明，變參數誤差補償算法大大降低了協作機器人極限位姿下的軌跡跟蹤誤差，極限位置下的平均位置誤差小于0.2 mm。其中，起始、終止以及中間時刻(25 s)的位置誤差較大，該區域誤差值變化較大，通過細化網格密度可進一步提高位置精度。所提方法可為協作機器人控制器的設計和剛柔耦合模型位置誤差補償的研究提供參考。