多源異構數據貝葉斯變權融合可靠性評估模型

唐 莉，程世娟，張曉潔，蔣玉婷

(1.西南交通大學 數學學院， 成都 611756; 2.西南交通大學希望學院 基礎部， 成都 610400)

0 引言

科技的不斷進步和新型材料的不斷出現，使產品的壽命越來越長，這些高長壽命產品在正常試驗條件下在短時間內的失效數據較少，這些小樣本攜帶的信息量不足以支撐傳統的統計分析。很多研究學者開始探索信息融合的方法，為小樣本可靠性評估提出了一些新的研究思路[1]。

王鳳飛等[2]通過融合歷史退化數據和失效壽命數據，發現多源信息融合可以提高剩余壽命預測的準確性。貝葉斯方法在信息融合計算方面有著廣泛應用，基于貝葉斯理論，賈祥等[3]融合不同的專家經驗信息和壽命試驗數據來擴充可靠性信息；王博等[4]融合多類型研制試驗數據來評估航天閥門的可靠性；Papananias等[5]融合不同來源和制造階段的數據和信息來提高產品質量。為了提高融合的精準度，有學者考慮在進行數據融合之前，先對信息源給予一個加權處理，比如，王保昌等[6]基于相關函數的多源信息融合方法實現了多個驗前分布的融合；文獻[7-10]分別采用自適應加權數據融合、利用指數衰減函數度量傳感器觀測值的相互支持程度、通過定義一致性和可靠性測度進行數據融合權值分配、提出一種基于最優權值的數據加權融合等方法，實現了傳感器信息數據的加權融合。張金槐[11]提出了產品驗前信息和現場信息進行融合的可信度加權融合方法；Zhang等[12]提出了一種新的加權數據融合方法，該方法可以計算多組先驗數據的定量可信度。對先驗信息的加權融合有了較深研究后，邵松世等[13]采用似然權重系數對不同來源可靠性信息的可信程度進行了量化，再基于貝葉斯方法實現了多源先驗信息的融合及可靠性分析。

以上研究解決了多個先驗信息如何進行加權，再與現場信息進行融合的問題，但是其研究僅考慮了不同先驗分布的權重，對于多個不同信息源數據信息的變權融合研究甚少。Berger指出先驗分布對離群值有較好排除能力的理論[14]，以此理論作為準則，在考慮現場真實數據對先驗分布權重影響的情況下，實現各個信息源的權重分配，提出一種對多源異構壽命數據信息進行變權融合的貝葉斯可靠性評估模型。

1 權重的確定

多源指試驗信息具有多種信息源，異構指這些信息源的數據類型或特征等不一致，在統計學領域認為這類數據不屬于同一總體，簡稱多源異構數據。下面討論獨立異構的壽命信息如何進行加權融合。

假設信息源獲取數據的環境條件相同，并將這些數據信息看作是傳感器對同一物理量采集到的。記n1,n2,…,nN表示N個信息源分別所對應的樣本數，x(i)={xi1,xi2,…,xini},i=1,2,…,N表示第i個信息源下獨立同分布的樣本；并假設第N個信息源為現場試驗信息源獲取的真實現場數據。

1.1 各信息源權重的確定

根據各信息源獲取的數據信息x(i)={xi1,xi2,…,xini},i=1,2,…,N所反應的總體分布特征，選擇適合各信息源的分布類型，擬合得到分布Fi(θ;x)，求得各信息源的似然函數Li(x(i)|θ)，其似然函數的尾部梯度特征[15]可表示為：

(1)

由現場試驗數據x(N)=(xN1,xN2,…,xNnN)，求得其似然函數LN(x(N)|θ)的尾部梯度特征為：

(2)

若通過查閱資料等途徑獲得參數θ的先驗分布為φ(θ;u1,u2,…,uk)，其中u1,u2,…,uk為先驗分布中的超參數，當關于θ的先驗信息在其分布的尾部區域取值θ0時，即可得到上述各信息源的尾部梯度特征值τi(Li(x(i)|θ0)),i=1,2,…,N和τN(LN(x(N)|θ0))，比較各信息源和現場試驗數據的尾部梯度特征值的絕對值差可得

hi=|τN(LN(x(N)|θ0))-τi(Li(x(i)|θ0))|,

i=1,2,…,N

(3)

當信息源的尾部特征和現場試驗數據的尾部特征越靠近時，說明此信息源和現場試驗數據越相似，信息源的可信度也越高，所占的權重也應該更高。即各信息源和現場試驗數據的尾部梯度特征值的絕對值誤差越小，此信息源數據信息所占的權重越大。故各信息源的權重可確定為：

(4)

2 確定各信息源的先驗信息

2.1 有先驗分布的情形

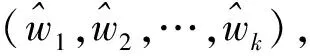
(5)

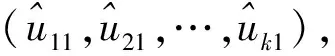
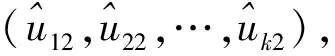
i=1,2,…,N

(6)

2.2 無先驗分布的情形

若無關于參數θ的任何先驗信息，根據Fisher信息陣的理論知識[16]，基于第i個信息源的數據信息x(i)=(xi1,xi2,…,xini),i=1,2,…,N得到其概率分布fi(x;θ)，得似然函數為：

計算出參數θ(單參數情形)的Fisher信息陣：

因此，單參數場合下的無信息先驗密度函數為：

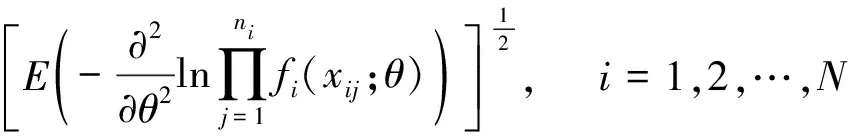
(7)

3 基于貝葉斯變權融合的可靠性分析

結合前文獲取的各信息源權重εi和先驗分布φi(θ|x(i)),i=1,2,…,N，以及第N個現場信息源壽命數據關于參數θ的似然函數LN(x(N)|θ)，采用貝葉斯估計法[17]，考慮對各信息源數據信息估計的先驗分布進行加權處理，并且將通過現場試驗獲得的信息融合到先驗信息的估計中，得到一個更客觀、合理的先驗分布，再以現場試驗數據作為樣本信息。最終，得到N個信息源數據信息融合后，關于參數θ的聯合后驗密度為：

φ1,2,…,N(θ|x(1),x(2),…,x(N))=

(8)

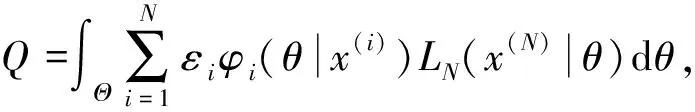
(9)

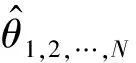
(10)

4 仿真分析

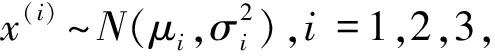
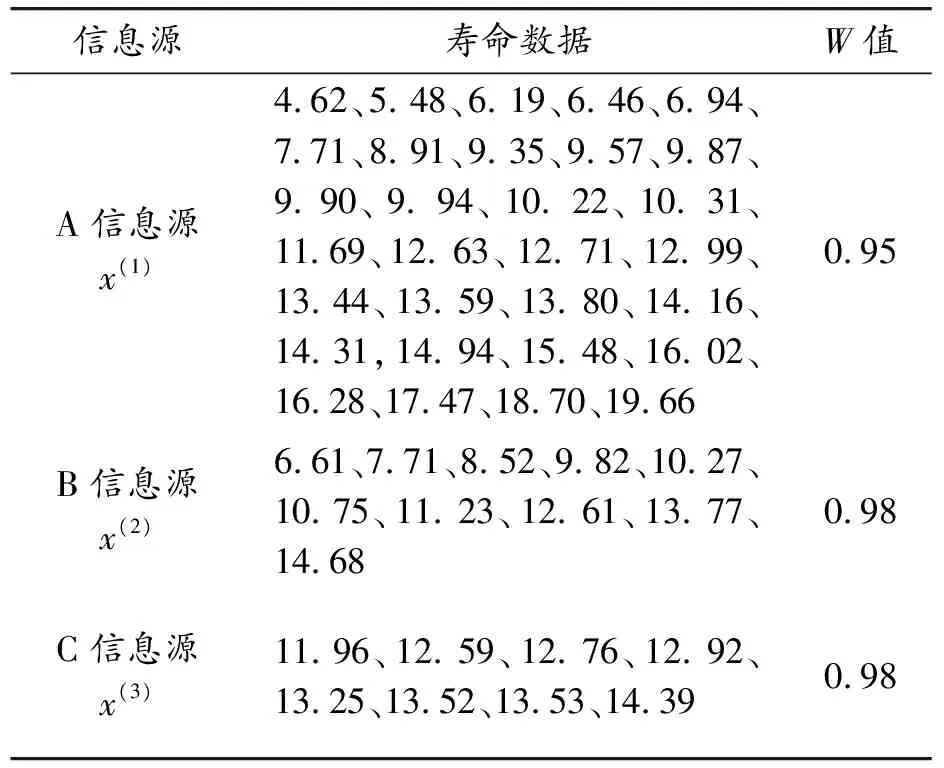
表1 不同信息源數據 年

采用2種變權方式：

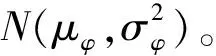
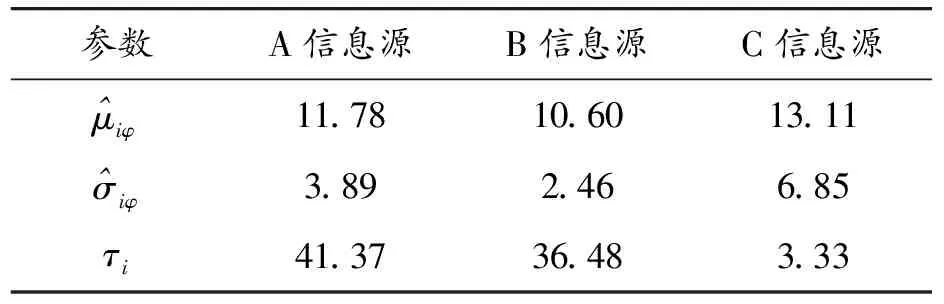
表2 3個信息源先驗分布的參數估計結果

根據式(1)和式(2)，計算得到A、B、C信息源的尾部梯度特征分別為：

τA=41.37，τB=36.48，τC=τ0=3.33

在參數μ的先驗正態分布的尾部3σ域內取值μ0=32.65時，根據式(3)和式(4)，獲取各信息源的權重占比(見表3)分別為：

εA=0.23，εB=0.27，εC=0.50

根據式(8)，可以寫出3源樣本數據變權融合后，關于平均壽命參數μ的后驗密度為：

φA,B,C(μ|x(1),x(2),x(3))=

由式(9)，得到在平方損失函數下，產品的平均壽命為：

2) 假設僅對A、B 2個信息源(不考慮現場試驗數據對參數μ先驗信息的影響)進行加權融合，同理求解，得到A、B信息源的權重占比為：

此時的后驗密度為：

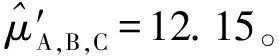
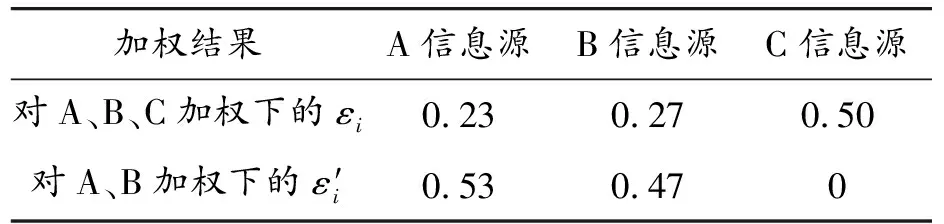
表3 不同加權方式的權重結果

為驗證各組壽命數據經過變權實現融合所得到的融合結果，相較于等權融合而言，更具真實有效性，此處使用相同數據，采用貝葉斯理論進行3源等權融合[18]，可得到3源等權融合后的后驗分布為：

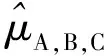
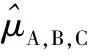
表4 3種不同融合方式獲取參數的檢驗結果

利用表1—4中的數據及參數估計的檢驗結果可知，通過極大似然法得到A、B、C源的平均壽命分別為11.78、10.60、13.11年，在3源加權、僅對A、B信息源加權和3源等權的3種變權情況下，進行數據融合，獲取融合后的平均壽命分別為12.81、12.15、10.87年，說明3源加權融合的評估結果更客觀合理，驗證了加權融合方法的有效性、合理性。

3源信息均變權進行融合后，得到產品的總體失效密度函數為：

可靠度函數的貝葉斯估計為：

式中：Φ(·)為標準正態分布的分布函數。在3種不同變權融合方式情形下，得到融合前后的可靠度函數曲線，如圖1所示。

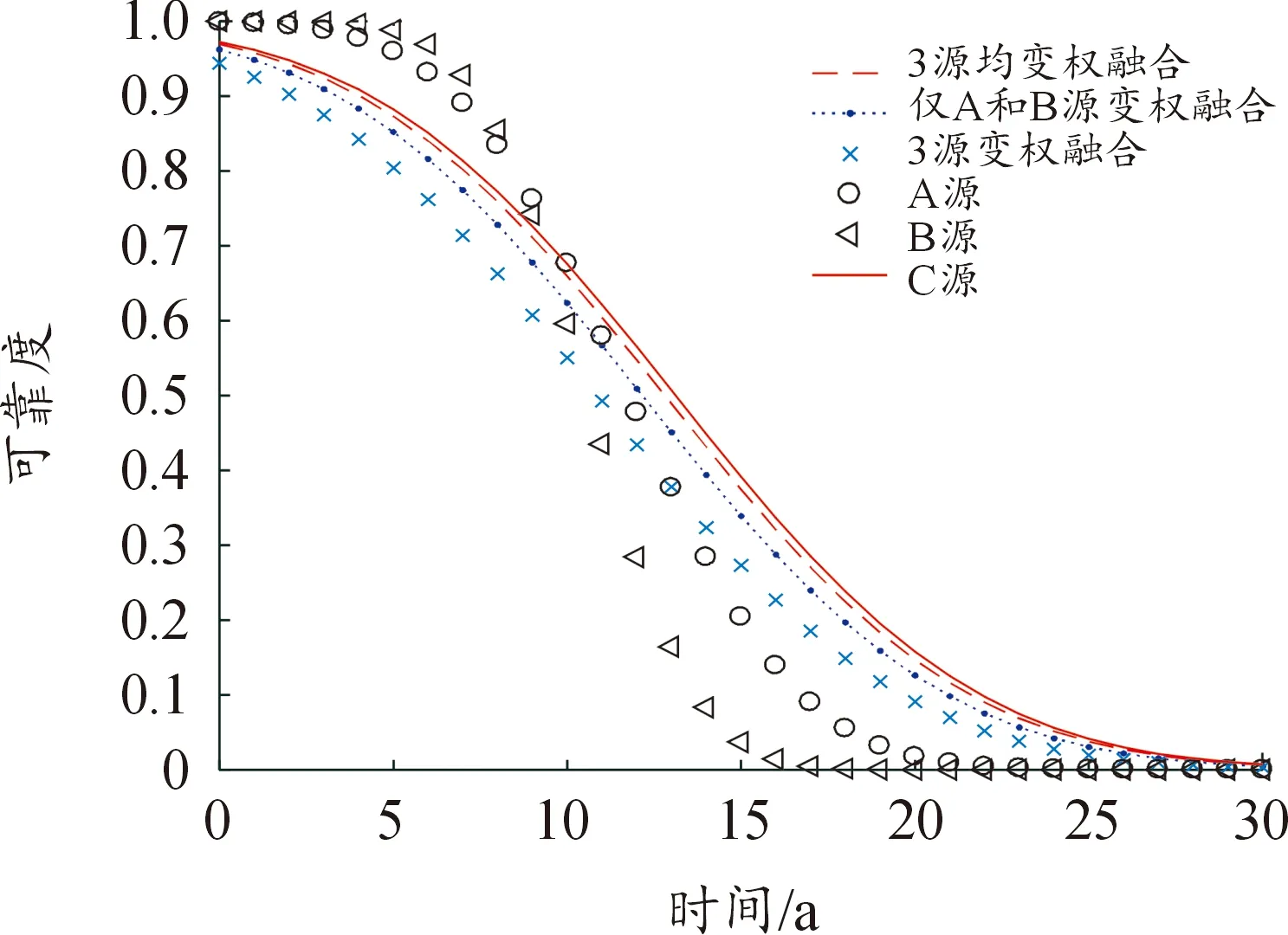
圖1 3源數據在不同加權融合情況下的可靠度函數曲線

通過圖1發現3源均變權和僅對A、B變權，2種融合方式得到的可靠度函數結果，介于3源等權融合和C源現場數據融合結果之間，并且3源均變權的結果更靠近C源現場數據的結果，可知變權融合效果優于等權，3源均變權的融合效果優于僅對A、B信息源變權，3源變權融合后的分布總體明顯更接近真實現場試驗數據的分布總體。因此，將現場試驗數據融入先驗信息，考慮對各信息源權重占比的影響，使得利用貝葉斯方法做數據融合估計時，先驗信息中含有更全面、更客觀的參數信息，能更科學合理地評估產品的可靠性。

5 結論

針對小樣本數據，提出了基于貝葉斯理論進行多源壽命數據變權融合的可靠性評估模型，獲得產品的壽命分布信息及可靠性特性。仿真結果表明，該模型簡單易操作，考慮了現場試驗數據對參數先驗和各信息源權重占比的影響，可以提高評估精準度。從信息論的角度而言，利用各種途徑獲取的信息數據，避免資源浪費，能夠得到對產品更科學合理的可靠性評估分析結論，在統計決策方面也有更好的穩健性，為產品后續的預測研究奠定了基礎。