基于STSS模型的改進及其應用

匡 嬋,鄭海濤,趙宜嬋,韋洪雷

(西南交通大學 數學學院， 成都 611730)

0 引言

隨著信息技術的迅猛發展和大數據時代的到來，以環境、交通、金融、醫療等為代表的多個領域產生大量數據，這些數據中蘊含著豐富的時空信息。例如醫學成像數據[1]、環境監測衛星遙感數據[2-3]、國家環境信息中心數據集NCEI(national centers for environmental information)等。針對不同類型的時空數據，需要找到合適的表達來描述數據反映出的各項信息。而采用合適的模型來對不同類型的時空數據進行分析，會提高對時空特性探究的準確度，以及對數據變化趨勢有更真實的描述，這對時空數據的應用發展有著重要的意義。

近年來，國內外關于不同類型時空數據的應用研究都是比較頻繁的。例如，Cabrera等[4]通過廣義加性混合模型建立時空數據模型來觀察天氣和登革熱傳播之間的復雜關系，這項研究匯集了來自不同來源的大型數據集，包括委內瑞拉衛生部，還包括美國國家航空航天局提供的遠程衛星氣候數據。再例如，Ghosh等[5]提出了一個端到端的交通關聯規則挖掘框架，通過分析城市的出租車出行軌跡，有助于提取城市交通動態，此研究使用NYC綠色和黃色出租車跟蹤、羅馬出租車數據集和舊金山出租車數據集的真實GPS跟蹤數據集，屬于軌跡數據類。而許熳靈等[6]也同樣使用軌跡數據，他們基于智能交通卡數據，以南京市為例，通過建立一種季節性差分自回歸移動平均模型，解釋了不同種類的天氣因素(如降雨、氣溫、相對濕度、風速等)對地鐵客流量時空分布的影響程度。

對于收集到的一些海量的、有噪聲的數據進行平滑處理是了解其時空特征的關鍵。例如，對于NARCCAP(the North American regional climate change assessment program)[7-8]這樣的大規模時空數據集，French等[9]提出了一種平滑處理方法STSS(spatio-temporal sandwich smoother)。在2013年Xiao等[10]提出的OSS(the original sandwich smoother)的基礎上，發展了一種懲罰樣條方法來表示具有主光滑成分的連續時空數據，分別對空間和時間維度采用不同的基函數來進行處理，他們還用模擬和實際數據證明了此方法的實用性。French等提出的STSS模型不僅能在保留數據時空特性下對數據做平滑處理，還具有高效的計算效率。而NCEI收集到的數據集不僅具有大規模的特性，還包含各種不同的信息變量。針對呈現出多維信息的時空數據，需要合適的表達來描述這類時空數據的特征。

French等提出的STSS模型能在時間、空間上捕捉到關鍵特征，但當協變量對響應有影響且有周期特征時，STSS模型還是不能很好地解釋數據的變化。因此，引入了協變量函數和周期函數。協變量函數用來描述各種信息變量對響應變量的影響，而周期函數用來補償解釋數據的周期性。利用STSS模型關于基函數和懲罰函數的運用，可以對大規模數據進行平滑處理；同時還伴隨著協變量和周期性對觀察變量的影響。關于協變量函數使用的是常見的多元線性模型，而周期函數則考慮了不同周期長度的描述，這樣能探究出數據更真實的周期變化。為了更好地處理上述類型的時空數據，提出的模型不只是單一地討論數據的時空結構，也可以觀測其相關信息對數據變化的影響，還包括探測數據變化是否具有一定的周期性，這樣的結合使得所提的模型能更全面、更貼合實際地描述時空數據的結構和變化。

論文的結構如下：第1節介紹了所提出的改進模型，包括模型的表達形式和參數估計方法；第2節利用蒙特卡洛的方法對所提出的模型進行了模擬研究；第3節將改進模型應用于實際時空數據集，并對分析結果進行了討論；第4節對所提出的方法進行了總結。

1 模型介紹

對于一些數據集，它們收集的區域范圍廣，統計年份長，呈現出大規模的數據集，還包含著多種信息變量，并且數據變化存在明顯的周期性。而期望能在對數據做平滑處理的同時，還能觀察一些相關因素對數據的影響和數據的周期變化情況，因此在French等提出的STSS模型基礎上，引入了協變量函數和周期函數。關于描述協變量與響應變量之間的關系使用的是常見的多元線性模型，周期函數則也考慮了不同周期長度的描述。下面是關于模型的具體介紹。

1.1 模型表達

假設在某個區域內觀測到n1個不同地點和n2個不同時間的響應，用數學模型可表示成

yij=y(xij;si,tj)=

f(xij)+d(tj)+z(si,tj)+ε(si,tj)，

i=1,2，…,n1,j=1,2，…,n2

(1)

其中：y是響應變量，f(x)是有關影響y的協變量x的函數，d(t)是關于時間t的周期函數，z(s,t)是考慮成空間位置s和時間t對y的一個影響，誤差過程ε(s,t)滿足Ε(ε(s,t))=0，Ε(ε2(s,t))=σ2。如上文所述，考慮f(x)是關于x的多元線性函數，z(s,t)則是使用STSS模型的方法，即空間基函數和時間基函數的張量積，令

其中：p是協變量的個數，C是一個由周期函數構成的矩陣，殘差εij=ε(si,tj),1≤i≤n1,1≤j≤n2，這里的周期函數d(t)可以采用如下形式：

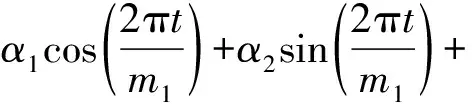
(2)

其中：α1,α2,…,α2k-1,α2k是函數的系數，2k是周期函數的個數，m1,m2,…,mk取值為正整數。在應用于實際數據的時候，可以綜合考慮周期呈半年、季度以及月度等的變化來確定k和m1,m2,…,mk的取值，以便觀察數據更真實的周期性。則周期函數矩陣也可以表示成

則上述數學模型(1)可以表示成矩陣的形式：

y=Xβ+Cα+Bθ+ε

(3)

式(3)中，基函數的張量積B=B2?B1，其中B1、B2分別是關于空間和時間的基函數矩陣，具體形式如下：

其中：rk(si),1≤k≤c1,1≤i≤n1是描述空間的徑向基函數，bl(tj),1≤l≤c2,1≤j≤n2是描述時間的B樣條基函數。

這里采用的徑向基函數是Wendlend協方差函數[11]，基本形式為：

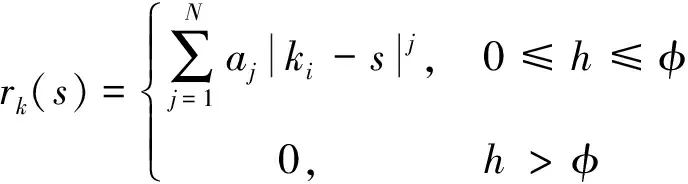
其中：k=1,2,…,c1，h=|ki-s|是空間中2點之間的距離，ki,i=1,2,…,c1表示空間節點，N是多項式階數，φ是函數的支撐(也稱帶寬參數)，aj,j=1,2,…,N為一組非零系數。關于Wendland協方差函數的更多細節可以在文獻[11-12]中找到。采用的B樣條基函數的一個遞歸定義[13-14]如下，設τ0≤τ1≤…≤τM為一組時間節點，記第i個d次B樣條基函數為Bi,d(t)，定義

其中i=0,1,…,M-1。當節點數M和次數d確定時，得到一組B樣條基bl(t),1≤l≤c2，其中c2=M+d+1。

1.2 參數估計

在給定的懲罰參數λ1、λ2下，關于上述模型(3)的目標函數可表示為：

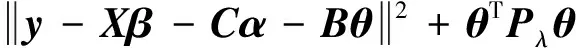
(4)

其中

λ1λ2(Dm)TDm?(Sm)TSm

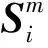
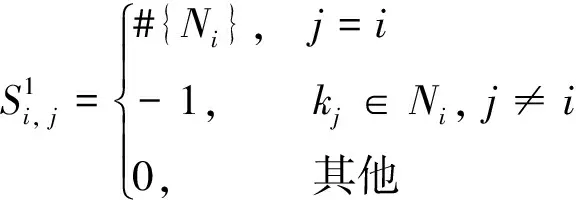
其中#{Ni}為近鄰集Ni元素的個數；當m≥2時，定義

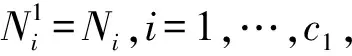
則依次計算出Sm的每一行元素。關于空間差分矩陣更多的運用細節可以在French等的文章中找到。懲罰參數λ1、λ2可通過廣義交叉驗證[15-17]的方法進行選擇。

令參數

q是周期函數系數的個數，根據1.1小節的描述可知q=2k，則上述目標函數(4)可以轉化為以下形式：

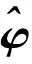
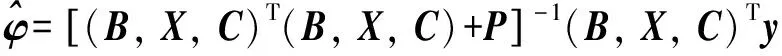
(B,X,C)Ty

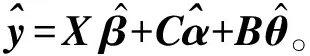
2 模擬研究

根據所提出的模型隨機生成數據，然后進行多次模擬，來觀察其參數估計的結果、模型擬合的效果以及模型殘差的分析結果，模擬設置如下：

1) 樣本容量n=n1×n2×n3，n1、n2是關于空間位置的樣本大小(一共有n1×n2個空間位置)，n3是時間長度的樣本大小。模擬取5×5個空間點，分小樣本n=5×5×50、中樣本n=5×5×200和大樣本n=5×5×500。

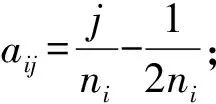
3) 根據2得到空間維和時間維的基函數矩陣B1、B2和差分矩陣Sm、Dm；確定周期函數矩陣，模擬將周期矩陣設置為：

由上述的模擬設置，在不同的樣本容量和標準差的情況下，各進行了1 000次的重復模擬，最后取每個參數估計結果的均值。與參數模擬取值的比較如表1—3所示，從估計結果看，取不同大小的樣本容量以及不同的標準差，得到的估計值與模擬取值相差都比較小。模擬數據的周期函數系數僅α1、α2取值不為零，其余的周期系數均取值為零，而其余的周期函數系數α3、α4、α5和α6的估計都非常接近于0，則可以說明周期項得到的估計結果與模擬數據周期項也非常相近，即可以說明提出的模型能反映數據的真實周期變化。參數估計結果的均方差(MSE)如表1—3括號中的數值所示，表中數據顯示隨著樣本容量的增加均方差在逐漸減小，而隨著標準差取值的增加均方差也在增加，其各均方差值也都比較小，表示參數估計結果的波動比較小。

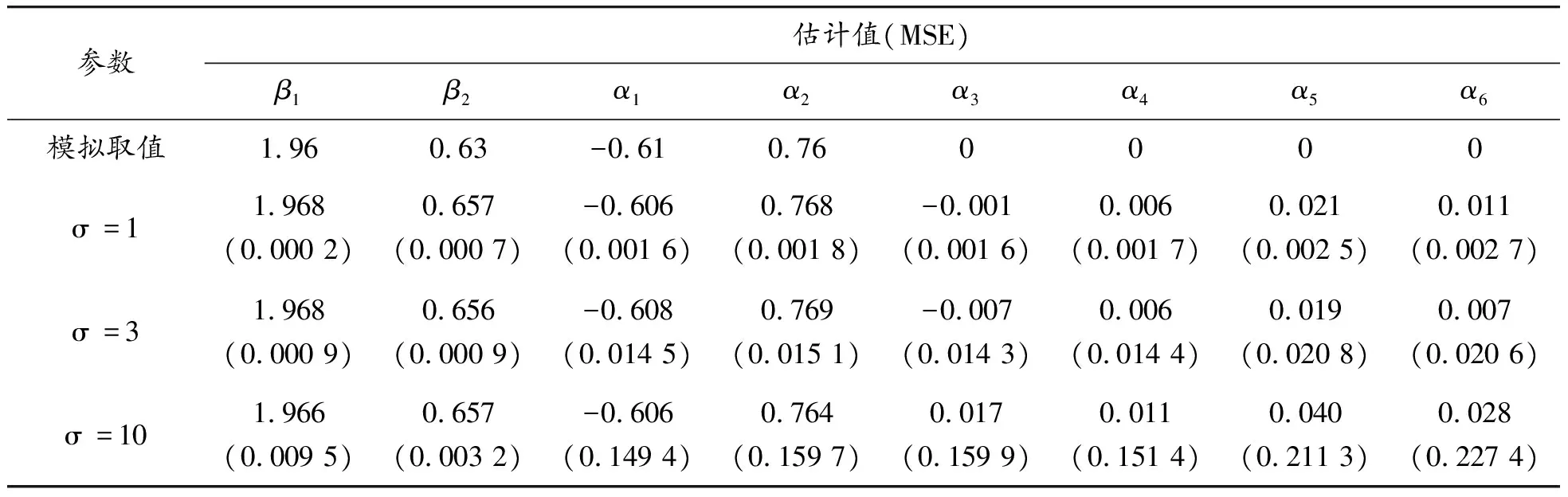
表1 小樣本模擬數據參數估計結果

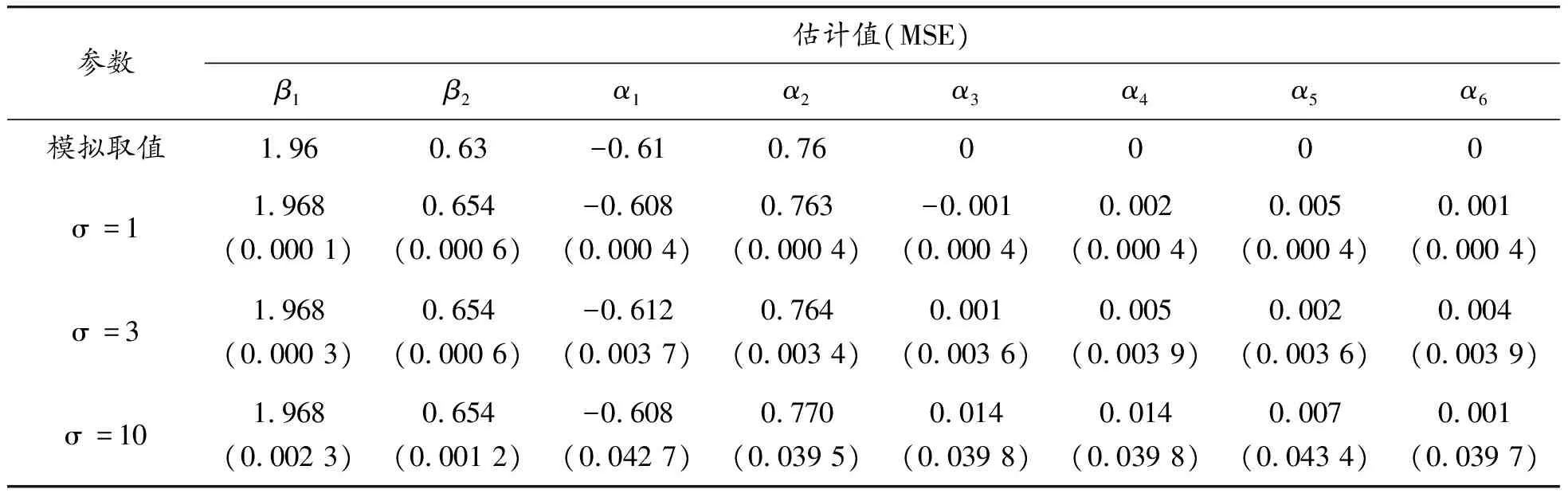
表2 中樣本模擬數據參數估計結果

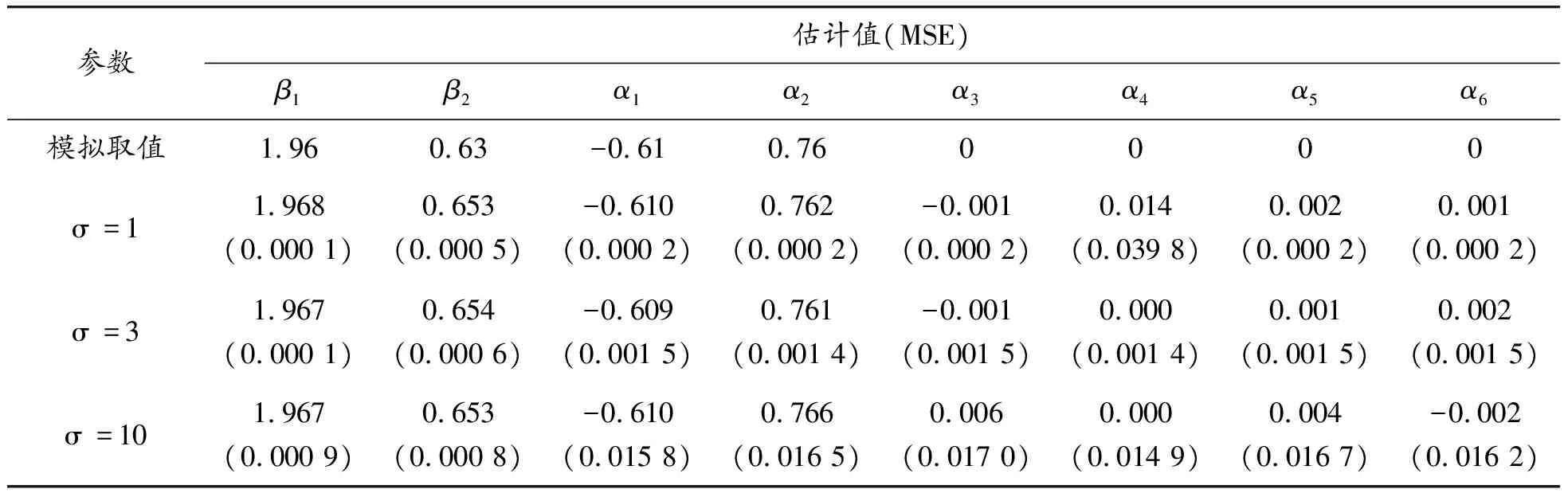
表3 大樣本模擬數據參數估計結果

任意選取一個空間位置，在3種樣本大小和3種標準差的情況下，分別觀察模型的擬合效果。圖1是同一空間位置的觀測值與擬合值，其中紅色實線為觀測值，綠色虛線為擬合值。如圖1所示，可以看到圖中的擬合效果都是比較好的，而隨著標準差取值的增加會使得其擬合值與觀測值之間的差變大。從任一位置的擬合圖形可以看到，不管是小樣本、中樣本還是大樣本，其模型的擬合效果都是非常好的，隨著標準差取值的增加，觀測值的波動會稍微變大，而擬合值會相對平滑一些。此外，還對任一空間位置進行了殘差分析，結果顯示不同樣本不同標準差情況下的殘差都呈現出非常好的隨機性和正態性。各種殘差圖形以及正態性檢驗結果如圖2—4和表4所示，表4中顯示檢驗的P值均大于0.05，可判斷殘差服從正態分布。也就意味著所提出的改進模型有較好的適用性，下面通過實際數據的應用來證實模型的實用性。

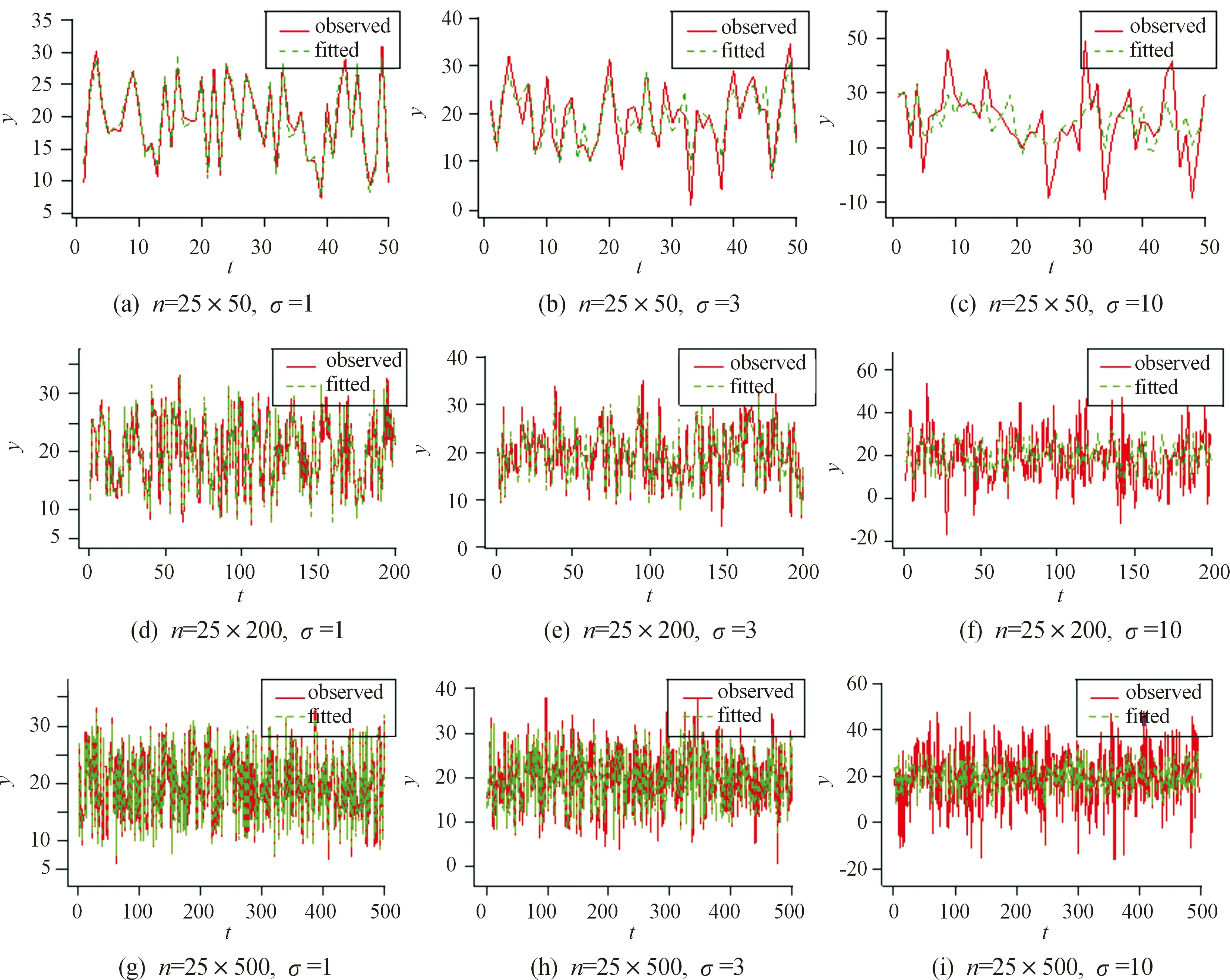
圖1 3種樣本容量不同標準差下的擬合圖

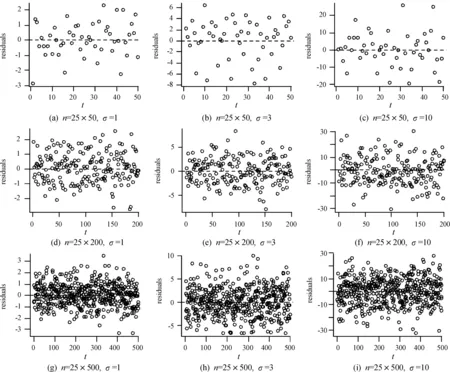
圖2 3種樣本容量不同標準差下的殘差圖

圖3 3種樣本容量不同標準差下的殘差Q-Q圖

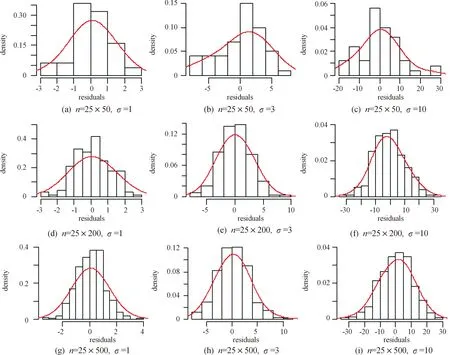
圖4 3種樣本容量不同標準差下的殘差直方圖

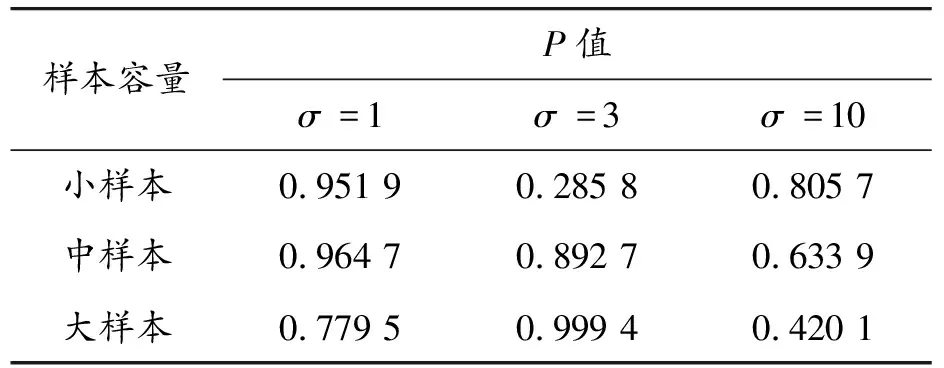
表4 殘差的正態性檢驗(Kolmogorov-Smirnov)結果

3 案例分析

在這一節中將用上述改進的模型應用于實際時空數據，并與STSS模型做比較。實際應用的時空數據是由NCEI收集的數據集。隨機選取美國的Colorado州中57個站點的月平均溫度(華氏度)數據，將此作為待觀測的響應變量，其中各個站點的空間位置由經緯度表示，時間長度為從2000年1月到2020年12月，形成了252個月份內在57個空間位置觀測到的時間序列，總共有14 364個響應值。圖5中的黑色圓點表示各個站點的位置。其余的信息變量還包括各個站點的海拔和月降水量，將這2個信息變量作為待觀測數據的協變量。

現在考慮將改進的模型應用于這些數據。在關于基函數的處理上，空間維度使用2種不同分辨率下的Wendland協方差函數，分別使用4節點和20節點(共24個節點)，每個分辨率的節點位置在圖5(b)中用不同顏色和形狀的符號表示，采用m=2階的空間差分懲罰；時間維數使用了12個B樣條基函數。為了能更準確地抓住數據的真實周期變化，這里考慮設置周期函數的個數為q=16和正整數取值(m1,m2,…,m8)=(2,4,6,8,10,12,24,36)。

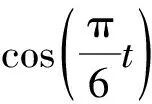
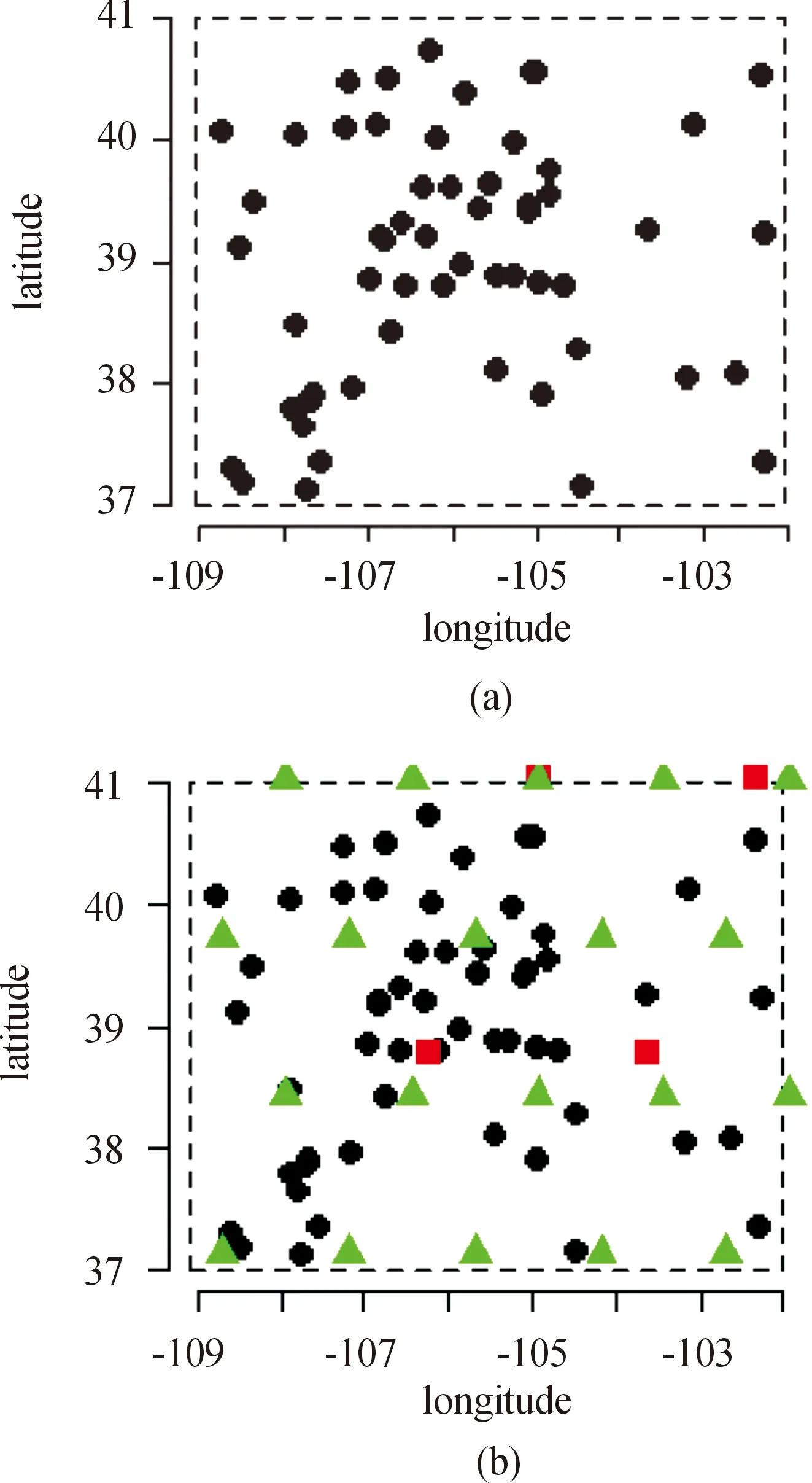
圖5 Colorado州中57個站點的位置

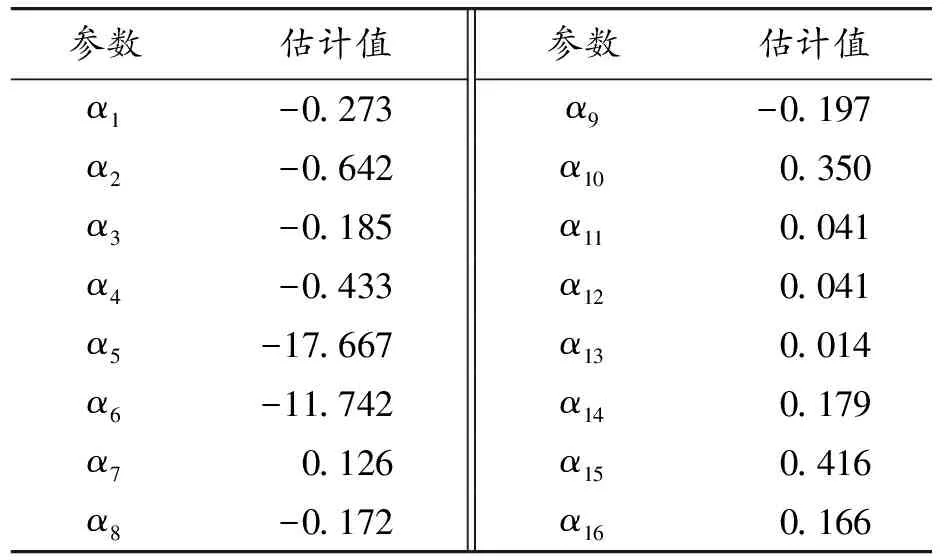
表5 周期函數參數估計結果

接下來將觀察模型的擬合效果和殘差分析。圖6是選取的任一站點位置的擬合圖，圖中紅色實線為月平均溫度的真實觀測值，綠色虛線為擬合值。從圖6可以看到2條線非常貼合，說明模型的擬合效果是很不錯的。圖7是整體殘差的相關圖形，圖7 (a)是整體殘差圖，圖7 (b)是殘差直方圖，殘差圖中的數值大致均勻分布在零均值線上下，從圖7可以看到,整體殘差的隨機性和正態性都表現得很好，說明模型適用于實際時空數據。

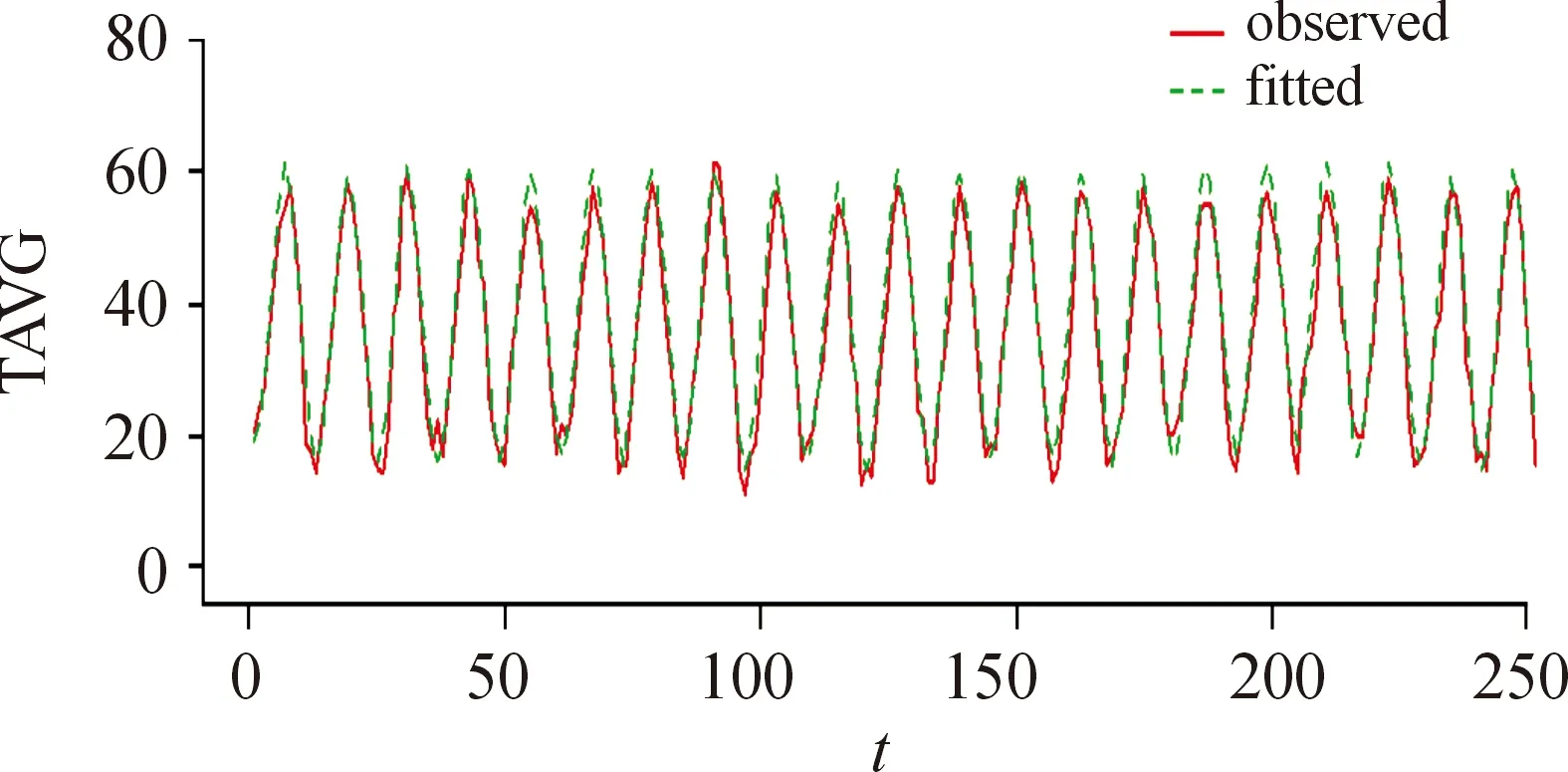
圖6 任一站點位置的擬合圖

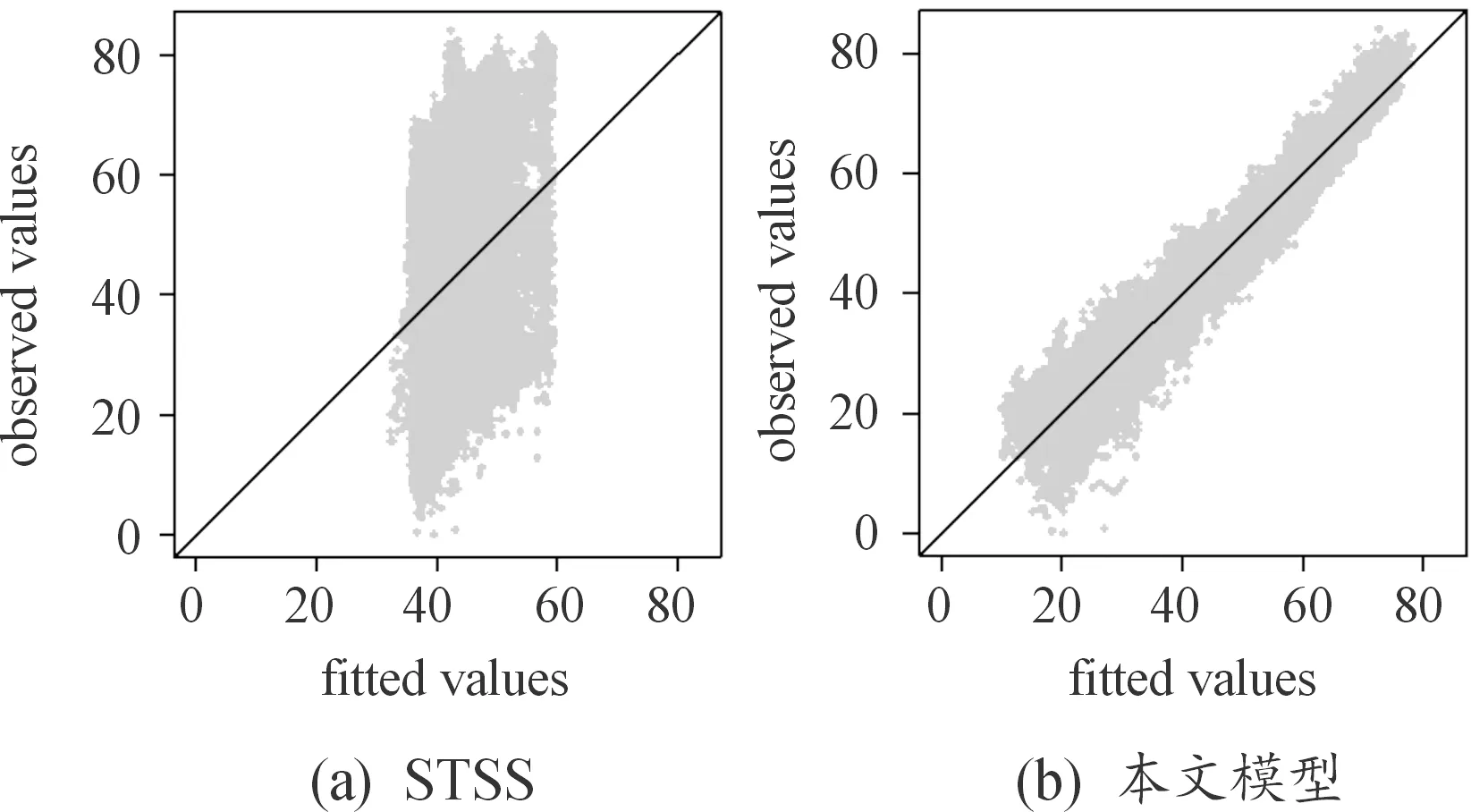
圖8 觀測到的月平均溫度(華氏度)和擬合值的散射圖

表6是2個模型的均方差比較，從表中數值可以看出，改進模型的均方差比STSS模型小很多，說明改進的模型要比STSS模型更適合于時空數據。圖8分別是2個模型的擬合數據和觀測數據的散射圖，其中圖8(a)是STSS模型，圖8 (b)是本文模型的散射圖，顯示了變量之間期望的線性關系，可以看到改進的模型比STSS模型能更完整地捕獲原始月平均溫度數據的總體模式。

表6 模型的均方差

French等提出的STSS模型具有高效的計算效益和很好的數據結構捕獲效益，但也提到在應用STSS模型時，會因為模型中的一些調整參數的不同設置導致模型得到的結果存在差異。例如，基函數的節點數，太少會導致擬合結果過于平滑，但節點數太多又會使得基函數的參數增多從而使得計算量增大；再比如，帶寬參數φ的選擇，French等建議至少是每個節點與其近鄰點之間最大距離的2倍，但φ太大也會導致計算不穩定，因為生成的基函數矩陣將具有高度相關的列。還有基函數的階數、差分矩陣的階數m，等等。也就是說，在應用于實際時空數據的時候，有時會因為一些原因使得模型的這些調整參數不一定取到最合適的數值，這樣會很容易降低模型的使用效益，也會減少模型的實用性。而從圖8(a)和圖8(b)的對比結果可以看到，提出的改進模型會大大減少這種情況對結果產生的影響，能在一定程度上有效地保證模型的使用效益，從而確保模型的實用性。

4 結論

在French等提出的STSS模型基礎上進行了改進，使其更適用于包含多維信息的大規模時空數據。在STSS模型上引入了協變量函數和周期函數，協變量函數描述各信息變量對觀察變量的影響，周期函數描述數據的周期性。其中關于協變量與觀察變量之間的關系使用的是常見的多元線性模型，而周期函數則考慮了不同周期長度的描述。與STSS模型相比，所提的改進模型既能在保留時空結構下對數據做平滑處理，還可以觀測其相關因素對數據的影響，探測數據變化的周期性。然后通過模擬實驗和NCEI收集的實際時空數據應用驗證了改進模型的適用性和實際性。

模擬研究結果表明，改進的模型呈現較好的擬合效果，而隨著數據標準差取值的增加，觀測值的波動稍微變大，模型的擬合更趨于平滑。此外，模型的殘差在各種情況下都呈現良好的正態性，即顯示了改進的模型有很好的適用性。將改進的模型應用于實際時空數據，分析結果呈現了良好的擬合效果，顯示了改進模型的優良性。與STSS模型進行對比，改進的模型比STSS模型能更完整地捕獲原始數據的整體變化。