考慮充電調度的電動無人車配送路徑規劃問題研究

曹珍　韓曙光

摘 要： 在充電站有充電容量約束的情況下，研究充電調度電動無人車配送路徑規劃問題。首先以極小化車隊中電動無人車的最大行駛距離為目標，構建數學規劃模型，為電動無人車車隊安排配送路徑，使得各車的行駛距離盡可能均衡；其次應用動態規劃算法（Dynamic programming algorithm， DP）求解小規模算例，改進遺傳-模擬退火算法（Genetic-simulated annealing algorithm， GA-SA）優化較大規模算例的電動無人車路徑和充電策略；最后對相關因素進行靈敏度分析，以驗證所提出算法的可行性與合理性。結果表明：DP算法解小規模算例表現良好；改進GA-SA算法與單純遺傳算法（Genetic algorithm， GA）相比，求解大規模算例時優化的路徑效果更佳，且大大縮短電動無人車車隊的最長子路徑的長度和總行駛距離。該研究可以為物流公司的電動無人車配送業務發展提供參考，幫助企業提高電動無人車的運輸效率和服務水平，降低配送成本。

關鍵詞： 電動無人車；配送路徑規劃；充電容量約束；充電調度；動態規劃；遺傳-模擬退火算法

中圖分類號： O223.1；O223.4

文獻標志碼： A

文章編號： 1673-3851 （2023） 11-0784-11

引文格式：曹珍，韓曙光.考慮充電調度的電動無人車配送路徑規劃問題研究［J］. 浙江理工大學學報（自然科學），2023，49（6）：784-794.

Reference Format： CAO Zhen， HAN Shuguang. Research on the distribution routing problem of electric unmanned vehicle considering charging scheduling［J］. Journal of Zhejiang Sci-Tech University，2023，49（6）：784-794.

Research on the distribution routing problem of electric unmanned vehicle considering charging scheduling

CAO Zhen， HAN Shuguang

Abstract：? Under the restriction that the charging station has charging capacity constraints， we focus on researching the distribution routing problem of electric unmanned vehicles with charge scheduling. A mathematical programming model was firstly established with the objective of minimizing the maximum travel distance of electric unmanned vehicles of the fleet， so as to arrange the distribution path for the unmanned vehicle fleet and balance the travel distance of each vehicle as much as possible. Secondly， dynamic programming （DP） algorithm was applied to solve small-scale examples， and genetic-simulated annealing algorithm （GA-SA） was improved to optimize the route and charging strategy of electric unmanned vehicles for large-scale examples. Finally， related factors were analyzed to verify the feasibility and rationality of the proposed algorithm. The results show that the DP algorithm performs well in solving small-scale examples. Compared with the simple genetic algorithm （GA）， the improved GA-SA can get a more reasonable solution when solving large-scale examples， and greatly shorten the length of the longest sub-path and the total driving distance of the electric unmanned vehicle fleet. This study can provide reference for the development of electric unmanned vehicle distribution business of logistics companies， help enterprises improve the transportation efficiency and service level of electric unmanned vehicles， and reduce distribution costs.

Key words： electric unmanned vehicles; distribution route planning; charging capacity constraints; charging scheduling; dynamic programming; genetic-simulated annealing algorithm

0 引 言

近年來，隨著能源價格不斷上漲，電動無人車在城市物流配送環節逐漸成為傳統內燃機汽車的替代品，但電動無人車在實際配送中面臨電池續航能力不強、充電設施不足等問題。因此，研究電動車輛（Electric vehicle，EV）的路徑規劃和充電策略，對于推廣電動無人車進行物流配送具有重要的現實意義。

傳統的車輛路徑規劃問題（Vehicle routing problem，VRP）最早由Dantzig等［1］提出，是組合優化中研究最廣泛的問題之一，至今已有大量的相關研究成果。張玉州等［2］考慮救災物資車輛路徑規劃問題，極小化救災車輛的總運輸距離，根據任務緊急度設計了任務再分配策略的遺傳算法（Genetic algorithm，GA），優化了應急物資的配送路徑；Tamke等［3］研究有二維裝載容量約束的車輛路徑規劃問題，設計了分支切割算法求解。隨著綠色環保的電動汽車的普及與發展，電動車輛路徑規劃問題（Electric vehicle routing problem，EVRP）擴展了傳統的VRP問題，逐漸成為路徑規劃的研究熱點。葛顯龍等［4］結合部分充電策略建立整數規劃模型，設計了混合模擬退火算法（Simulated annealing algorithm，SA），優化了電動汽車的物流配送路徑；揭婉晨等［5］考慮了客戶需求可拆分的情況，通過改進分支定價算法求得EVRP問題的最優解；Wu等［6］采用自適應調整信息素揮發因子和突變算子，提出了一種混合的蟻群算法以求解帶時間窗的EVRP問題。以上研究的優化目標多是極小化總行駛距離；然而，在實際生活中，物流公司追求的往往不是尋求整個車隊的總行駛距離最短，而是均衡利用車輛，降低電池的退化率。該問題的優化目標可以描述為極小化車隊中車輛的最大行駛距離，這類問題稱為最小最大車輛路徑規劃問題（Min-max vehicle routing problem，MMVRP），如在線m-steiner旅行商問題［7］、災區無人機監控［8］等均屬于該類問題。

目前MMVRP問題的相關研究主要集中在近似算法和啟發式算法上。當無固定倉庫點，起點任意且車輛的數量k也任意時，Yu等［9］給出了一個5-近似算法；隨后Yu等［10］證明了MMVRP問題的最壞情況界下界為5/4；Yakc［11］考慮了單配送中心的最小最大車輛路徑規劃問題，采用蟻群優化以及其他隨機方法分配客戶給車輛，進一步用3-opt方法局部優化；Sze等［12］研究了有容量約束的MMVRP問題，通過并行貪婪插入方法生成初始解，再利用自適應變量鄰域搜索改進；李小川等［13］根據問題特征并結合人工魚群算法的尋優思想，提出了一種精英反向學習魚群算法來解決MMVRP問題。近些年智能物流配送逐漸發展，研究最小最大電動車輛路徑規劃問題（Min-max electrical vehicle routing problem，MMEVRP）具有一定的現實意義；然而以上帶充電的路徑規劃研究往往都忽略了充電站容量問題，一般假設一個充電站可同時容納無數車輛充電。

近年來已有學者開始研究充電站有容量約束的充電路徑規劃問題以及相關求解算法。例如：Bruglieri等［14］考慮了充電站內的充電樁數量有限的電動車輛路徑問題，基于弧變量建立混合整數規劃模型，設計割平面的方法精確求解小規模算例；李默涵等［15］考慮了充電站內車輛排隊等待充電的時間對路徑成本的影響，采用自適應大規模鄰域搜索算法求解路徑；Keskin等［16］研究充電站出現排隊情況對路徑選擇的影響，考慮依賴排隊時間的分段線性充電，使用自適應大鄰域搜索可行空間和確定可行路徑。

雖然有關充電站有容量約束的路徑規劃問題研究已取得了一定的進展，但涉及充電站有容量約束的MMEVRP問題研究相對較少，且現有模型并沒有考慮充電等待時間。本文在上述研究基礎上，結合物流配送的實際狀況，針對充電站有容量限制的情況，以極小化車隊中電動無人車的最大行駛距離為目標，結合充電等待時間建立了可多次完全充電的混合整數規劃模型，研究電動無人車的路徑規劃和充電調度。最后應用動態規劃算法（Dynamic programming algorithm，DP）和改進遺傳-模擬退火算法（Genetic-simulated annealing algorithm，GA-SA）求解該模型，并通過Solomon標準算例驗證算法的有效性和策略的可行性。電動無人車路徑規劃研究可為物流企業運營調度車輛提供決策性參考意見。

1 問題描述與模型構建

1.1 問題描述

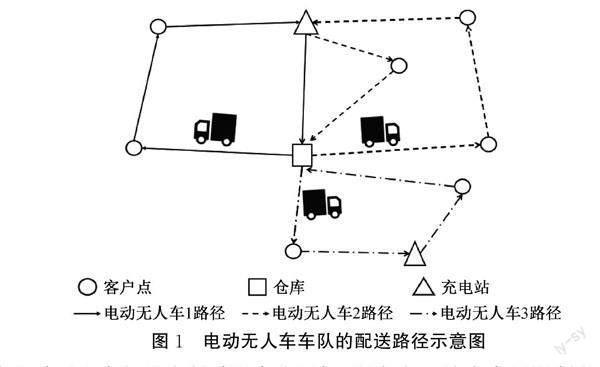
假設某物流快遞公司配有一個配送中心，另有若干個充電站點，充電站的充電樁數量有限，由若干數量的裝載容量和電池容量均相同的電動無人車組成配送車隊給客戶派送貨物。在不超過車輛的裝載容量的情況下，電動無人車充滿電后出發，完成配送任務后返回配送中心；由于車輛的電池容量有限，在行駛過程中可能需要根據實時電量前往充電站進行充電。例如：受充電站數量限制，電動無人車1和電動無人車2在行駛過程中需要前往同一個充電站補充電量，此時可能存在排隊等待充電的情況，對應的電動無人車車隊的配送路徑示意圖如圖1所示。本文作如下假設：a）為保證交付效率，每個客戶只訪問一次；b）電動無人車以恒定速度行駛，且電池電量消耗系數恒定，消耗的電量與行駛距離呈線性關系；c）充電站內的充電樁數量有限，每個充電樁充電功能均正常，且充電速率一樣；d）當電動無人車前往充電站充電時，車輛的電池總是充滿電離開的；e）電動無人車在客戶點停留過程中不消耗電量；f）不考慮客戶點與充電站的時間窗限制。

以極小化車隊中電動無人車的最大行駛距離為目標，研究充電站有容量限制的電動無人車的路徑規劃和充電調度問題，合理地安排各無人車的行駛路徑和充電計劃，以滿足客戶的配送需求，盡可能減少充電次數和排隊充電等待時間，均衡各無人車的工作時長。

1.2 MMEVRP數學模型構建

本文中的符號及其含義見表1。無向圖j表示配送網絡；V=｛C∪F′∪｛o｝｝表示全部點的集合；E=（i，j）i，j∈V，i≠j表示弧集，每條弧關聯一個非負的行駛時間tij和距離dij；車輛集合K是由電池容量和裝載容量均相同的同一車型組成，表示至多有k輛無人車可以被分配來執行送貨任務。

考慮充電站容量有限的電動無人車車輛路徑規劃問題數學模型如下：

式（1）表示極小化車隊中電動無人車的最大行駛距離；式（3）—（4）表示所有客戶點的貨物僅由一輛電動無人車配送一次；式（5）—（6）表示電動無人車均從配送中心出發，最終返回配送中心；式（7）表示到達和離開同一點的弧的數量相等，即每個點需保持流量平衡；式（8）表示消除不包含配送中心的子回路；式（9）表示電動無人車的載貨能力限制；式（10）表示電動無人車從客戶點i行駛到客戶點j時，載重量的變化約束；式（11）表示電動無人車的電池電量的變化；式（12）表示到達任意客戶點的電量和離開該客戶點的電量是一樣的，即在客戶點處不耗電池電量；式（13）表示電動無人車的電池電量不大于電池容量；式（14）表示電動無人車在充電站的充電量；式（15）—（16）表示每輛電動無人車到達各節點的時間變化約束；式（17）表示電動無人車在充電站處完全充電所需時間；式（18）表示在充電站處電動無人車等待充電的時間；式（19）表示0-1變量約束。

2 模型求解

2.1 動態規劃算法

傳統的VRP問題是NP難問題，而最小最大電動車輛路徑規劃問題是VRP問題的擴展，因此MMEVRP問題也是NP難問題。由于該問題的復雜性，大部分研究利用GA算法或蟻群算法等啟發式算法求解，這些算法通常可以在較短的時間內得到解，但無法保證解的質量，因此本文先采用可精確求解的DP算法求解此問題。

DP算法常用來解決多階段決策過程的優化問題，在路徑規劃方面也有較好的應用成果，利用DP算法求解最優路徑可以節省反復搜索可行路徑的時間。

由袁森等［17］證明的引理可知，最小最大圈覆蓋問題的最優解將客戶集C恰好劃分成了k個子集，構成集合C=｛S1，S2，…，Sk｝。為解決小規模的MMEVRP問題，首先逆時針依次篩選出一定角度范圍內的所有客戶點，這些客戶點的貨物需求之和不能超過無人車的裝載容量，所有客戶點恰好分成k個客戶集合，分別由k輛車派送。

DP算法可快速求解MMEVRP問題小規模實例，但隨著問題規模的增大計算時間會呈指數型增長，導致算法性能降低，甚至可能無法求解出問題的最優解，因此精確算法在求解大規模實例時不再適用。此時需要利用尋優性能好的啟發式算法對大規模算例進行求解，本文改進GA算法能在可接受時間內得到問題較好的全局最優解。

2.2 改進遺傳-模擬退火算法

GA算法是源于生物界的啟發式算法，是一種高效的隨機全局搜索優化方法，常用來求解各種車輛路徑規劃問題。為更好地求解電動無人車的配送路徑以及選取合適的充電站充電，本文對GA算法進行了兩個方面的改進。首先為優化充電站位置的選取與充電策略的選取，設計了一個充電站最優插入策略；其次由于GA算法容易陷入局部最優，引入Metropolis準則，以一定概率接受劣質解，增大算法迭代過程中的搜索空間，提高所提出算法的求解質量。

改進遺傳-模擬退火GA-SA算法的主要步驟如下：

a）確定染色體編碼規則。在模型求解過程中，要確定電動無人車數量、每輛車需要服務的客戶集合以及訪問的充電樁，采用自然數編碼會比較直觀得到每輛無人車的配送順序，用o表示配送中心，用1，2，…，n表示對應的客戶點，n+1，n+2，…，n+p表示配送網絡中的充電樁編號，即配送網絡中一共存在p個充電樁（包括虛擬充電樁），最后在起點和終點分別插入配送中心，即構成1條染色體。

b）計算適應度函數。適應度函數用于評價種群中染色體優劣以及趨近于最優解的程度，適應度越大，表明染色體質量越高，被選擇的可能性越大，本文的目標函數是使得車輛的最大距離最小，取目標函數f的倒數作為適應度函數fit（i）。

c）選擇算子。基于對個體適應度的評估，計算種群的每個個體的fit（i），遺傳概率為pi=fit（i）/∑nj=1fit（j），計算個體累計概率為qi=∑nj=1pj，最后采用輪盤比例選擇適應度較大的個體進入下一次迭代。

d）設計搜索算子。使用部分匹配交叉和基因倒位插入變異兩種策略進行尋優。鄰域尋優策略示意圖如圖2所示。交叉操作分別在兩個染色體中隨機截取相同大小的基因片段，拼接到另一個染色體前端，再將拼接后的兩個染色體中與拼接基因重復的基因刪去，部分匹配交叉操作的示意圖如圖（a）所示；在一個染色體上隨機挑選兩個基因片段互換位置。這樣可以保證種群的多樣性，避免交叉操作引起的局部收斂，變異操作的示意圖如圖（b）所示。

e）運用自適應Metropolis準則。對原始種群進行GA算法的選擇、交叉、變異等操作后，形成新一代種群，再運用Metropolis準則增強算法的局部搜索能力，分情況選擇個體。若新解w′的目標函數f（w′）小于初始解w的目標函數f（w），即f（w′）

f）選擇充電站插入。由于車輛的電池容量有限，配送過程中要考慮電動無人車的電量情況。GA算法構造的未插入充電站的初始路徑解中可能存在違背距離約束的配送路徑，因此，這些路徑還要插入充電站，對應車輛需要去充電站補充電量。由于配送網絡中含有的充電站數量相對較少，所以電動無人車在充電站處可能產生等待時間。

為此本文設計了一個充電站最優插入策略，改進GA-SA算法流程如圖3所示，具體步驟如下：

步驟1。找出所有未插入充電站的解中違背距離約束的不可行配送路徑。

步驟2。在不可行配送路徑中，找到電動無人車出發后電量低于電池安全電量閾值α之前能到達的最遠客戶點，此時安排該車輛前往附近充電站充電，若不能到達則轉步驟4，否則轉步驟3。

步驟3。對當前在該充電站內的電動無人車按到達充電站（站內有m個充電樁）時間順序進行編號｛n1，n2，…，ni｝，根據先到先充原則充電，若ni≤m，說明有充電樁空閑，車輛無需等待可馬上充電；若ni>m，說明車輛等待充電樁空閑才能充電，接在充滿電后離開此充電站的有最小編號的車輛nj（j

步驟4。電量低于電池電量閾值α時不能到達附近充電站視為不可行路徑，繼續迭代搜索可行路徑解。

步驟5。若所有車輛均完成貨物配送，則結束本次調度；否則重復以上步驟，直到達到迭代次數條件，結束算法。

3 實驗分析

本文使用Matlab 2016a與Python3.7編程語言對算例進行求解，運行環境為64位Windows操作系統，運行內存為4 GiB，處理器為Intel（R） Core（TM） i5-7200U CPU@2.50 GiHz 2.71 GiHz的計算機。選取Solomon標準測試集中部分數據［18］進行實驗，數據集根據客戶的分布特點分為三類：C類數據集的點是聚類分布的，R類數據集的點是隨機分布的，RC類數據集是半聚類半隨機分布的。

3.1 算例一分析

首先選取Solomon算例中C101的9個點作為基礎測試，編號0表示配送中心，編號5和9表示配送網絡中的充電站，站內只有單個充電樁，設配送中心內可使用的相同類型電動無人車最大數量為3，該類型的無人車的裝載容量為50 kg，距離約束為65 km，電池耗電系數為1.1 kWh/km，充電系數為100 kWh/h，恒定的行駛速度為60 km/h，利用DP算法可以快速求出具體路徑分別是：0-3-1-9-0、0-7-8-5-6-0、0-2-4-0。由于配送網絡中有2個充電站，3輛無人車只有2輛車前往充電站充電，此算例沒有等待時間，3條子路徑長度為77.97、68.53、63.22，因此車隊中電動無人車的最大行駛距離是77.9，該值即為目標函數值。各客戶點、倉庫點橫縱坐標X和Y的位置信息，以及算例一電動無人車配送路徑如圖4所示。

3.2 算例二分析

算例二以“數據類別-客戶點數量-充電站數量-每個站內充電樁數量”命名，例如“C101-40-1-2”表示在C101標準實例中選取前40個點進行實驗，取1個點為充電站，該充電站中有充電樁接口2個。設C101-40-1-2中配送中心編號為0，充電站編號為29，設配送中心中可使用的電動無人車最大數量為5輛，車輛的裝載容量為200 kg，距離約束為80 km，電池耗電系數為1.1 kWh/km，充電速率為100 kWh/h，行駛速度為60 km/h，電池電量閾值α設為20%，同時設定算法的最大迭代次數G=2000次，初始溫度為10000 ℃，冷卻因子為0.99，交叉概率為pc=0.9，變異概率為pm=0.1，變異次數為10次。目標是使得電動無人車車隊的最大行駛距離盡可能地小，合理調度充電車輛，減少充電次數以及排隊等待充電時間，提高配送效率。

利用單純的GA得到的目標函數值為196.16，車輛的總配送距離為925.83，無人車隊在充電站處共充電9次，充電時間共為552.63，等待充電時間為44.60，其中車輛1的充電等待時間達28.40，車輛4的充電等待時間為16.20，其他車輛充電沒有排隊等待時間；而使用本文提出的改進GA-SA求解的最小最大子路徑長度為100.51，車隊的總配送距離為498.11，電動無人車車輛在充電站共充電5次，總的充電時間為366.59，充電等待時間均為0。優化后的目標函數值，即最小最大子回路長度縮短了48.76%，電動無人車車隊的總行駛距離減少了46.20%，而且充電時間與等待時間也顯著減少，電動無人車配送工作效率提高明顯。

表2為改進GA-SA算法求解MMEVRP算例的求解結果，從表中數據可以看出，各無人車的路徑長度相差較小，工作時長較均衡，符合目標要求。改進GA-SA算法生成的電動無人車配送路徑如圖5所示，GA算法和改進GA-SA算法求解的優化過程收斂曲線對比如圖6所示，改進GA-SA算法在迭代1000次左右時逐漸收斂，得到最優目標函數值，雖然比GA算法的收斂速度慢，但是從適應度函數值的變化過程可看出本文改進的算法優化效果更佳，求解質量更優。

3.3 算例三分析

為了進一步驗證本文提出的算法求解不同類型和規模算例的性能，結合客戶總需求，假設可使用的無人車最大數量增加為8輛，其他參數設置同算例二，對一些算例進行仿真實驗，分別用未改進的GA算法和所提出的改進GA-SA算法單獨求解10次，記錄每次的運行結果、充電次數以及程序運行時間，將10次計算的平均運行時間和最優解對比記錄見表3。

從上述求解結果可以看出，本文所提出的改進GA-SA算法在求解不同類型和規模的MMEVRP實例時都給出了更優的配送路徑，安排更少的充電次數能夠滿足電量需求。在配送網絡完全相同的情況下，從目標函數列中可以看出對比未改進前結果，改進GA-SA算法縮短電動無人車車隊中最長子路徑的長度顯著，與單純的GA算法相比，優化率（未改進結果與改進結果的差值與未改進結果的百分比）達30%以上，極大地提高了電動無人車的配送效率。雖然算法的求解時間隨著問題規模的增大而增加，但求解結果更優、質量更高。可以預測，在求解更大規模的實際物流配送問題時，該算法也將表現出更快的求解速率和更好的優化性能，能合理有效地給出電動無人車車隊的物流配送路徑規劃和充電調度，給物流公司提供一些指導性意見。

3.4 影響無人車行駛距離的關鍵因素的靈敏度分析

在MMEVRP問題中，實驗的計算結果會受無人車數量和充電站中充電樁數量影響，因此下文將分析這兩個因素的改變對計算結果的影響。從C101中選取數據進行測試，客戶數為50，充電站數量為2，站內只有單個充電樁。

a）無人車數量。將電動無人車的耗電系數設為1.1 kWh/km，最多可使用的無人車數量分別設為3輛、5輛、7輛。電動無人車的數量與其最大行駛距離和總行駛距離的關系如圖7所示，從該圖可以看出電動無人車數量對不同算例的子路徑中的最大行駛距離和車隊的總行駛距離的變化趨勢。當電動無人車的耗電系數不變，車輛數量增加時，無人車隊中最長配送子路徑長度逐漸減小，這符合實際配送情況，所需要服務的相同客戶數量時，可使用的車輛數量越多，分配給各無人車的客戶數量會相應減少，因此配送路徑中的最大行駛距離會變小，但是車隊的總行駛距離相應的有所增加。車隊中的最大行駛距離和總行駛距離都受數據集中客戶點分布影響，由于R101和RC101數據中客戶點分布較分散，行駛過程中車輛的充電次數不可避免地增加，此時目標函數和總行駛距離都會比聚類分布的C101大。

b）車輛的耗電系數。將最多可使用的無人車數量設為5輛，車輛的耗電系數分別設為0.8、1.1 kWh/km和1.4 kWh/km，電動無人車耗電系數與無人車的最大行駛距離和總行駛距離的關系如圖8所示。從圖8可以看出，當電動無人車的耗電系數越來越大時，充電次數會有所增加，所以最大子路徑長度也會隨之增加，車隊行駛的總距離也逐漸增加。這符合實際情況，耗電系數越大，說明電動無人車行駛單位距離電池電量消耗的越多，而符合電量約束的可行路徑減少，電量不足時無人車需要多次前往充電站充電，所以會改變無人車的行駛路徑，這時各輛無人車的行駛距離以及車隊的總距離都會相應地有所增加。同樣地，由于數據集中客戶點分布情況不同，耗電系數增大時，較為分散的數據集R101和RC101行駛過程中充電次數增加的可能更多，此時子路徑的最長距離和車隊的總行駛距離都隨之增大。

由以上實驗可以看出，利用電動無人車在城市中配送貨物，可以通過增加電動無人車數量和開發新技術降低耗電系數使得最長子路徑距離盡可能地短，均衡各無人車的工作時長。

4 結 語

本文研究了在充電站有充電容量約束的情況下，考慮配送途中的充電次數以及可能存在的充電等待時間的電動無人車的路徑規劃和充電調度優化問題，建立了MMEVRP的數學規劃模型。針對小規模算例，應用DP算法精確求解無人車配送路徑；針對中大規模算例，改進GA-SA算法求解，增強算法搜索能力，避免算法陷入局部最優。數值實驗以及靈敏度分析結果表明，本文提出的優化算法可以減少充電次數以及充電等待時間，同時縮短車隊中最長子路徑的長度和車隊的總行駛距離，使得車隊中車輛的工作時間更加均衡，減少車輛的電池損耗率。本文為物流企業選取電動無人車來進行物流配送提供一定參考，幫助物流企業提高電動無人車的利用率和配送效率，降低物流公司的配送成本。

在實際城市無人物流配送系統中，還需考慮客戶點的服務時間窗口等其他限制，因此后續研究可以進一步考慮客戶時間窗的路徑規劃、部分充電的充電調度策略等。

參考文獻：

［1］Dantzig G B， Ramser J H. The truck dispatching problem［J］. Management Science，1959，6（1）： 80-91.

［2］張玉州，徐廷政，鄭軍帥， 等.考慮緊急度的救災車輛路徑問題建模與優化［J］.計算機應用，2019，39（8）：2444-2449.

［3］Tamke F， Buscher U. A branch-and-cut algorithm for the vehicle routing problem with drones［J］. Transportation Research Part B： Methodological， 2021，144：174-203.

［4］葛顯龍，李祖偉，葛小波.考慮靈活充電策略的帶時間窗物流配送路徑優化研究［J］.控制理論與應用，2020，37（6）：1293-1301.

［5］揭婉晨，侍穎，楊珺， 等.需求可拆分電動汽車車輛路徑問題及其改進分支定價算法研究［J］.管理學報，2020，17（12）：1873-1880.

［6］Wu H G， Gao Y L， Wang W T， et al. A hybrid ant colony algorithm based on multiple strategies for the vehicle routing problem with time windows［J］. Complex & Intelligent Systems， 2023， 9（3）： 2491-2508.

［7］Zhang Y B， Zhang Z， Liu Z H， et al.An asymptotically tight online algorithm for m-Steiner Traveling Salesman Problem［J］. Information Processing Letters， 2022，174：106177.

［8］Guo Q， Peng J， Xu W Z， et al. Minimizing the longest tour time among a fleet of UAVs for disaster area surveillance［J］. IEEE Transactions on Mobile Computing， 2022， 21（7）： 2451-2465.

［9］Zhang Y B， Zhang Z， Liu Z H，Yu W， Liu Z H.Improved approximation algorithms for some min-max and minimum cycle cover problems［J］. Theoretical Computer Science， 2016，654： 45-58.

［10］Yu W，Liu Z H.Better approximability results for min-max tree/cycle/path cover problems［J］. Journal of Combinatorial Optimization， 2019，37（2）：563-578.

［11］Yakc E.A heuristic approach for solving a rich min-max vehicle routing problem with mixed fleet and mixed demand［J］. Computers & Industrial Engineering， 2017，109：288-294.

［12］Sze J F，Salhi S，Wassan N.The cumulative capacitated vehicle routing problem with min-sum and min-max objectives：An effective hybridisation of adaptive variable neighbourhood search and large neighbourhood search［J］. Transportation Research Part B： Methodological， 2017，101：162-184.

［13］李小川，劉媛華，王影歌.求解最小最大VRP的精英反向學習魚群算法［J］.傳感器與微系統，2020，39（2）：140-143.

［14］Bruglieri M，Mancini S，Pisacane O. The green vehicle routing problem with capacitated alternative fuel stations［J］. Computers & Operations Research， 2019，112： 104759.

［15］李默涵，毛李帆，鄭從鎮， 等.考慮充電等待成本的電動汽車路徑問題［J］.廣東電力，2020，33（7）：33-41.

［16］Keskin M，Laporte G，atay B.Electric vehicle routing problem with time-dependent waiting times at recharging stations［J］. Computers & Operations Research， 2019， 107： 77-94.

［17］袁森，陳開奇，李江坤， 等.最小最大圈覆蓋問題的精確算法［J］.中國科學：信息科學，2022，52（6）：960-970.

［18］Solomon M M. Algorithms for the vehicle routing and scheduling problems with time window constraints［J］. Operations Research， 1987，35（2）： 254-265.

（責任編輯：康 鋒）

收稿日期： 2022-11-29網絡出版日期：2023-06-07

基金項目： 國家自然科學基金項目（12071436）

作者簡介： 曹 珍（1998- ），女，江西贛州人，碩士研究生，主要從事組合優化方面的研究。

通信作者： 韓曙光，E-mail：zist001@163.com