無應(yīng)力狀態(tài)法在系桿拱橋吊桿張拉控制中的應(yīng)用
詹遠(yuǎn)藝 朱智宇 周群

摘要:為研究無應(yīng)力狀態(tài)法在系桿拱橋吊桿張拉控制中的應(yīng)用,文章以某鋼箱系桿拱橋為研究對象,針對其吊桿張拉控制難題,提出了無應(yīng)力索長迭代求解新方法,并開展了背景工程中的實橋應(yīng)用,成功解決了其吊桿張拉控制難題。結(jié)果表明:無應(yīng)力控制法在系桿拱橋吊索張拉中的適用性良好,可進(jìn)一步在同類拱橋吊桿張拉控制中進(jìn)行推廣應(yīng)用。
關(guān)鍵詞:鋼箱;系桿拱橋;施工控制;無應(yīng)力;吊桿張拉
0引言
下承式系桿拱橋是拱橋建設(shè)領(lǐng)域的一大創(chuàng)新,主要應(yīng)用于一些建筑高度受限、地質(zhì)條件較差但又需要較大跨徑的地方,尤其在一些城市橋梁建設(shè)工程中,非常受到青睞。然而,系桿拱橋與其他有推力的大跨度拱橋施工方法不一樣,最大的區(qū)別在于系桿拱橋需要通過張拉吊桿完成體系轉(zhuǎn)換,吊桿的張拉控制也是整橋施工最核心的環(huán)節(jié),直接影響整座橋梁成橋內(nèi)力狀態(tài)[1-2]。
目前對于索力張拉控制主要有倒拆法、正裝-倒拆迭代法和無應(yīng)力狀態(tài)法等3種控制方法,前兩種控制方法以索力控制為主,但受吊桿張拉順序、吊桿張拉索力、環(huán)境溫度等因素影響較大,易造成最終成橋狀態(tài)與理論設(shè)計狀態(tài)偏差較大,施工控制難度較大[3-6]。無應(yīng)力狀態(tài)法則直接建立施工狀態(tài)與成橋狀態(tài)之間的關(guān)系,不隨結(jié)構(gòu)體系和外荷載的變化而變化,避免了施工過程的影響,很好地解決了系桿拱橋分階段施工的結(jié)構(gòu)問題,尤其在索結(jié)構(gòu)橋梁施工控制中應(yīng)用最為廣泛。
本文以某施工中的鋼箱系桿拱橋為研究對象,探討無應(yīng)力狀態(tài)法在系桿拱橋吊桿張拉中的應(yīng)用,為背景工程施工提供技術(shù)保障,為類似工程提供借鑒。
1 工程背景簡介
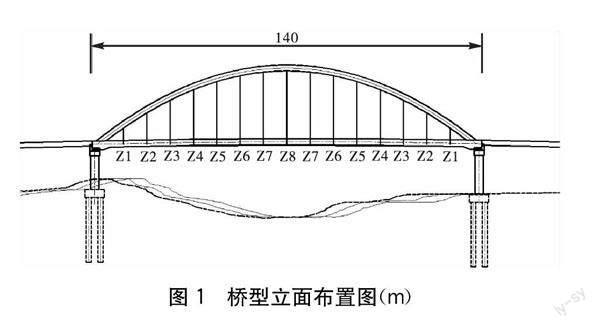
某城市跨河流主干路橋梁,主橋采用跨度為140 m的鋼箱系桿拱橋,橋面寬15 m,計算跨徑為136 m,矢跨比為1/5.0,拱軸線采用拋物線,主拱圈、橫撐均采用等截面鋼箱結(jié)構(gòu),橋面系縱橫梁均采用工字鋼結(jié)構(gòu),均為Q355鋼。橋型立面如圖1所示。
全橋吊桿共設(shè)置15對,間距為9.0 m,上下游對稱布置,依次編號為Z1-Z8(拱腳至跨中),均采用1 860 MPa級別的索體,型號為15.2-19。
為保證高精度的成橋索力及成橋線形,本項目考慮采用無應(yīng)力狀態(tài)控制法進(jìn)行吊索張拉,探討無應(yīng)力狀態(tài)法在系桿拱橋吊桿張拉中的應(yīng)用。
2 有限元模型的建立
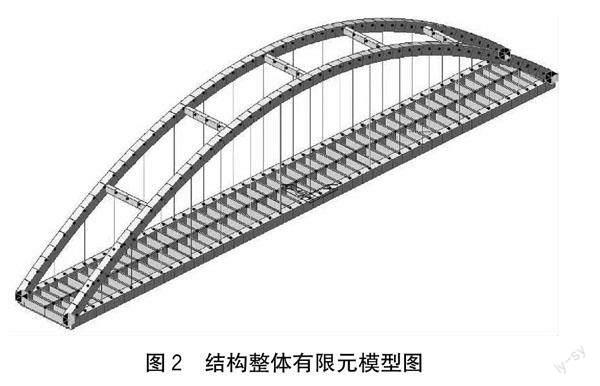
為探討無應(yīng)力狀態(tài)法在系桿拱橋吊桿張拉中的應(yīng)用,本文采用Midas Civil軟件建立結(jié)構(gòu)整體有限元模型,如圖2所示。
吊桿采用只受拉索單元進(jìn)行模擬,其余主梁結(jié)構(gòu)均采用一般梁單元進(jìn)行模擬。考慮到實際施工的滿堂支架主要提供豎向承載力,因此采用只受壓彈性支撐模擬滿堂支架。全橋共計423個節(jié)點,405個單元。
3 吊桿無應(yīng)力索長的求解分析
一般而言,無應(yīng)力狀態(tài)法計算結(jié)構(gòu)合理施工狀態(tài)是采用無應(yīng)力狀態(tài)量參數(shù)進(jìn)行控制,保證中間施工無應(yīng)力狀態(tài)量與合理成橋無應(yīng)力狀態(tài)量保持一致,成橋狀態(tài)與施工過程無關(guān)。本文吊桿無應(yīng)力張拉控制以吊桿無應(yīng)力索長作為控制量,即控制吊桿實際施工下料長度。
根據(jù)材料力學(xué)計算公式,吊桿無應(yīng)力索長計算公式為:
l=l0+(Nl0/EA)(1)
式中:l——吊桿有應(yīng)力索長(mm);
l0——吊桿無應(yīng)力索長(mm);
N——吊桿力(kN);
E——彈性模量(MPa);
A——吊桿截面積(mm2)。
由式(1)分析可知,已知吊桿力及吊桿有應(yīng)力索長,即可計算出吊桿無應(yīng)力索長。因此,吊桿實際施工控制可以設(shè)計成橋索力作為吊桿已知索力,設(shè)計成橋索長作為吊桿有應(yīng)力索長,即可求得吊桿無應(yīng)力索長。
當(dāng)然,吊桿作為索單元,應(yīng)考慮其軸向剛度與索力、索長、自重等所成的非線性關(guān)系,即吊桿彈性模量E在索單元計算中并非是固定值,一般考慮采用等效彈性模量法進(jìn)行迭代計算。
為解決這一非線性難題,本文提出一種吊桿無應(yīng)力索長有限元迭代計算方法,具體計算過程如下:
(1)建立全橋一次落架整體有限元模型,采用多點彈性支撐法、剛性橫梁法或未知荷載系數(shù)法對成橋設(shè)計索力進(jìn)行復(fù)核計算,保證所建模型與原設(shè)計基本一致。
(2)取設(shè)計成橋索力(一般由設(shè)計方提供)作為各吊桿索單元初拉力,采用NewZon-Raphson法進(jìn)行吊桿非線性(幾何非線性)分析,求解出吊桿無應(yīng)力索長。
(3)取(2)中計算得到的吊桿無應(yīng)力索長作為其索單元計算時無應(yīng)力索長初值,同樣采用NewZon-Raphson法進(jìn)行吊桿非線性(幾何非線性)分析,求解出各吊桿索力;與設(shè)計成橋索力作比對,求出差值,再反向加在上一步各吊桿索單元初拉力上,作為下一步各吊桿索單元初拉力。
(4)重復(fù)(2)、(3)的迭代計算,直至計算得到的成橋索力及無應(yīng)力索長誤差滿足精度要求。
經(jīng)過多個算例驗證,基于以上迭代計算得到的成橋索力誤差控制在<2%即可滿足吊桿無應(yīng)力索長前后兩次長度差值<1 mm,此精度完全滿足實際施工控制精度要求。
基于以上迭代算法,以設(shè)計圖紙上各吊桿理論索長(即理論有應(yīng)力索長,由吊桿在拱肋內(nèi)上錨點算至橫梁底錨墊板底面)為例,求得各吊桿無應(yīng)力索長及其對應(yīng)求得的成橋索力如表1所示。
由表1分析可知,經(jīng)多次迭代計算后(一般4、5次就能滿足精度要求),吊桿成橋索力誤差已控制在<2%,無應(yīng)力索長前后兩次計算差值最大為0.95 mm,已達(dá)到施工控制精度要求。
4 吊桿無應(yīng)力張拉控制分析
基于前文吊桿無應(yīng)力索長迭代計算方法即可求得全橋各吊桿高精度的無應(yīng)力索長,下文將在此基礎(chǔ)上以背景工程為研究對象,進(jìn)行吊桿無應(yīng)力張拉控制法的實橋應(yīng)用,總結(jié)歸納吊桿具體無應(yīng)力張拉控制過程如下:
(1)根據(jù)設(shè)計圖紙、拱肋實際成拱標(biāo)高、橋面標(biāo)高、預(yù)拱度等,精確計算成橋狀態(tài)下各吊桿實際索長(即實際有應(yīng)力索長,由吊桿在拱肋內(nèi)上錨點算至橫梁底錨墊板底面)。
(2)根據(jù)實際有應(yīng)力索長及前文迭代計算方法,精確計算出各吊桿實際無應(yīng)力索長。
(3)統(tǒng)一控制吊桿伸出量為25 cm(為方便量測,一般以伸出量20 cm或25 cm進(jìn)行控制),并計入吊桿下料長度中,即吊桿下料長度等于吊桿實際無應(yīng)力索長與吊桿伸出量之和。
(4)根據(jù)現(xiàn)場實際情況,制定施工最為方便的吊桿張拉順序進(jìn)行吊桿張拉,以每根吊桿伸出錨墊板的伸出量25 cm進(jìn)行控制。
以上4個主要步驟即吊桿無應(yīng)力張拉控制的核心過程。步驟1及步驟4相關(guān)注意事項如下:
步驟1中對實際拱肋及橋面系拼裝完成后的實際成拱標(biāo)高、橋面標(biāo)高等測量精度要求非常高,重點是對吊桿孔位進(jìn)行精確測量,在一些不易測量的位置可以考慮轉(zhuǎn)點,但一定需要保證測量數(shù)據(jù)的精度,以及計算結(jié)果的準(zhǔn)確性。
步驟4對于吊桿伸出錨墊板的伸出量25 cm也需要進(jìn)行嚴(yán)格控制,且盡可能采用受溫度影響較小的刻度尺進(jìn)行量測。
基于以上控制方法及控制要求,結(jié)合現(xiàn)場拱肋、橋面等實測數(shù)據(jù),求得吊桿實際無應(yīng)力索長、下料長度,計算結(jié)果如表2所示。
對比表1、表2分析可知,由精確測量的拱肋實際成拱標(biāo)高、橋面標(biāo)高、預(yù)拱度等計算得到的成橋狀態(tài)下各吊桿實際索長雖與設(shè)計圖紙理論索長有偏差,但根據(jù)實際索長采用本文第3節(jié)迭代計算方法求得實際無應(yīng)力索長,并以此實際無應(yīng)力索長求得的成橋索力誤差值仍能保證在2%以內(nèi),精度完全能滿足施工要求。
此外,采用無應(yīng)力狀態(tài)法進(jìn)行吊索的張拉控制只需要控制每根吊桿伸出錨墊板的伸出量25 cm即可保證成橋狀態(tài)吊索的索力精度,與實際施工過程無關(guān),即與吊索張拉順序無關(guān)。下文為驗證這一結(jié)論的準(zhǔn)確性,以及驗證無應(yīng)力狀態(tài)法在吊索張拉控制中的適應(yīng)性,制定了常見的3種吊索張拉方案,通過對比最終成橋索力是否一致來進(jìn)行驗證,并確定本橋吊桿合理張拉順序。具體張拉方案如表3所示。
根據(jù)以上吊桿張拉方案,建立吊索張拉順序的正裝模型,得出各方案詳細(xì)計算結(jié)果如表4所示。
由表4分析可知,各吊桿張拉方案中的最終成橋索力幾乎一致,且與表2一次成橋計算結(jié)果也幾乎一致。由此可見,無應(yīng)力狀態(tài)法在吊索張拉控制中是可行的,且同時證明了采用無應(yīng)力狀態(tài)法得到的成橋狀態(tài)只與無應(yīng)力索長有關(guān),與施工順序無關(guān)。
此外,對比不同張拉順序可知,雖然最終成橋狀態(tài)是一致的,但不同張拉順序?qū)?yīng)的吊桿施工階段最大張拉力(均在各吊桿張拉時達(dá)到最大)有所不同,表4中方案B吊桿施工階段最大張拉力優(yōu)于方案A與方案C,方案B相對更合理。
本文背景工程最終選擇方案B進(jìn)行吊桿無應(yīng)力張拉控制,張拉過程中通過液壓千斤頂油表讀數(shù)及吊桿伸出錨墊板的伸出量進(jìn)行索力與索長雙控,以吊桿伸出錨墊板的伸出量控制為主,千斤頂油表讀數(shù)為輔,最終成功完成全橋吊桿張拉。經(jīng)測量,錨墊板的伸出量最大誤差值≤3 mm,橋面實際成橋線形與設(shè)計線形吻合良好,最大誤差≤5 mm。
5 結(jié)語
本文以背景工程為研究對象,將無應(yīng)力張拉控制法成功應(yīng)用于系桿拱橋吊索張拉控制中,主要對無應(yīng)力索長的迭代求解方法,及無應(yīng)力控制法在吊索張拉中的具體應(yīng)用做了詳細(xì)的闡述,實橋應(yīng)用也充分證明了無應(yīng)力控制法在系桿拱橋吊索張拉中的適用性及方便性,可進(jìn)一步在同類橋型中推廣應(yīng)用。
參考文獻(xiàn):
[1]王家豪,張志程,徐 韜.無應(yīng)力狀態(tài)法在吊桿拱橋索力張拉控制中的應(yīng)用研究[J].湖南交通科技,2022,48(2):152-155.
[2]吳海軍,何 立,王邵銳,等.基于無應(yīng)力狀態(tài)法的大跨鋼管混凝土拱橋拱肋線形控制方法[J].橋梁建設(shè),2020,50(6):20-26.
[3]周 倩,周建庭,陳靜雯,等.鋼管混凝土拱橋扣索一次張拉索力優(yōu)化改進(jìn)算法[J].福州大學(xué)學(xué)報(自然科學(xué)版),2019,47(3):412-416.
[4]傅金龍,黃天立.鋼管混凝土拱橋吊桿張拉方案優(yōu)化研究[J].橋梁建設(shè),2016,46(4):67-72.
[5]周小勇,呂志敏,王加輝,等.支架現(xiàn)澆系桿拱橋吊桿張拉方案優(yōu)化[J].中外公路,2022,42(2):125-130.
[6]邵志向.鋼箱系桿拱橋無應(yīng)力狀態(tài)法施工控制研究[D].西安:長安大學(xué),2018.
作者簡介:詹遠(yuǎn)藝(1989—),工程師,主要從事橋梁設(shè)計工作。

