高考中概率統計問題的分析與展望
河北省廊坊市第一中學 楊明
通過對近幾年高考試卷的研究,發現概率統計模塊的考查更注重在數學知識交匯處命題,強調數學知識的綜合性與應用性。解答題中對于概率統計的考查,新高考數學試題朝著“重視基礎、強調綜合、體現應用與著力創新”等特點的命題方向發展。
一、強調綜合
“綜合性”主要體現在概率統計模塊的知識與其他數學知識之間的綜合與應用,特別是與函數、方程、不等式、數列等知識的交匯,同時與其他學科及數學思想方法的綜合。
例1數據顯示,中國直播購物規模近幾年保持高速增長態勢,而直播購物中的商品質量問題逐漸成為人們關注的重點。已知某顧客在直播電商處購買了n(n∈N*)件商品。
(1)若n=10,且買到的商品中恰好有2件不合格品,該顧客等可能地依次對商品進行檢查。求顧客檢查的前4件商品中不合格品件數X的分布列。
(2)抽檢中發現直播電商產品不合格率為0.2。若顧客購買的n件商品中,至少有2件合格產品的概率不小于0.998 4,求n的最小值。
解析:(1)由題意可知,X的所有可能取值為0,1,2。
所以X的分布列為表1。

表1
(2)記“顧客購買的n件商品中,至少有2件合格產品”為事件A,則P(A)=1-0.2n,由題意可知1-(1+4n)×0.2n≥0.998 4,所以(1+4n)×0.2n≤0.001 6,即(1+4n)×0.2n-4≤1。
設f(n)=(1+4n)×0.2n-4,則f(n+1)-f(n)=(5+4n)×0.2n-3-(1+4n)×0.2n-4=-16n×0.2n-3<0,所以f(n+1)<f(n),因為f(5)=21×0.2=4.2>1,f(6)=25×0.04=1,所以當n≥6 時,f(n)≤1成立,所以n的最小值為6。
點評:借助超幾何分布的計算、分布列的確定及概率中最值問題的應用等,將概率統計知識與函數等相關知識加以綜合。“綜合性”不是數學知識、思想方法等的“大雜燴”,而是借助創新情境來合理創設,充分把學科間、知識間、思想方法間的不同要素加以綜合與聯系。
二、體現應用
“應用性”的要求主要體現在同學們能夠以生產生活情境中的實際問題,融入閱讀能力,學科綜合,應用意識等,借助數學抽象與數學建模,綜合邏輯推理、數學運算和數據分析等,對問題進行合理的判斷、識別與決策。
例2數學建模是高中數學核心素養的一個組成部分,數學建模能力是應用意識和創新意識的重要表現。為全面推動數學建模活動的開展,某學校舉行了一次數學建模競賽活動。已知該競賽共有60名學生參加,他們成績的頻率分布直方圖如圖1所示。
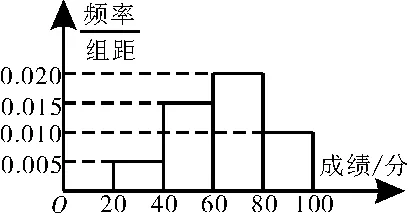
圖1
(1)為了對數據進行分析,將60分以下的成績定為不合格,60分以上的成績定為合格。為科學評估該校學生數學建模水平,決定利用分層隨機抽樣的方法從這60名學生中選取10人,然后從這10人中抽取4人參加座談會。記ξ為抽取的4人中成績不合格的人數,求ξ的分布列和數學期望。
(2)已知這60名學生的數學建模競賽成績X服從正態分布N(μ,σ2),其中μ可用樣本平均數近似代替,σ2可用樣本方差近似代替(用一組數據的中點值作代表),若成績在46分以上的學生均能得到獎勵,本次數學建模競賽滿分為100分,試估計此次競賽受到獎勵的人數。(結果根據四舍五入保留到整數位)
附:若X~N(μ,σ2),則P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3。
解析:(1)由頻率分布直方圖和分層抽樣的方法,可知抽取的10 人中合格的人數為(0.01+0.02)×20×10=6,不合格的人數為10-6=4,故ξ的所有可能取值為0,1,2,3,4。
故ξ的分布列為表2:

表2
(2)由題意可知,μ=(30×0.005+50×0.015+70×0.02+90×0.01)×20=64。
σ2=(30-64)2×0.1+(50-64)2×0.3+(70-64)2×0.4+(90-64)2×0.2=324,所以σ=18。
由X服從正態分布N(64,182),可得P(64-18<X≤64+18)=P(46<X≤82)≈0.682 7,則0.682 7)≈0.158 65,P(X>46)≈0.682 7+0.158 65=0.841 35,60×0.841 35≈50。
所以此次競賽受到獎勵的人數為50。
點評:綜合頻率分布直方圖、分層抽樣、正態分布、隨機變量的期望與方差等,實現問題的實際應用。高考試題設計注重實際應用,借助概率統計的分析結果,合理作出相應的科學決策。
三、著力創新
“創新性”的要求主要體現在同學們要具有獨立思考能力,具備批判性和創新性等思維方式。高考概率統計模塊的試題經常通過創新情境的探究性或開放性來設置,或探究應用,或開放結論,全面發展同學們的個性,并有效增強其創新意識與創新應用。
例3空氣質量指數AQI與空氣質量等級的對應關系如表3所示:
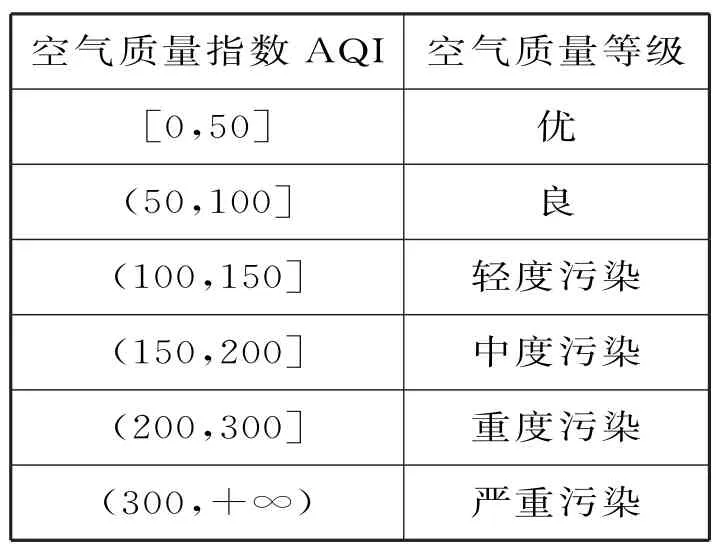
表3
某場館記錄了一個月(30天)的情況,如表4所示:

表4
(1)利用表4,估算該場館日平均AQI的值。(利用這組數據所在區間的中點值來代表對應組中的數據)
(2)如果把頻率視為概率,且每天空氣質量之間相互獨立,求未來一周(7 天)中該場館至少有兩天空氣質量等級達到“優或良”的概率。(參考數據:0.77≈0.082 4,結果精確到0.01)
(3)為提升空氣質量,該場館安裝了2套相互獨立的大型空氣凈化系統。已知每套凈化系統一年需要更換濾芯數量情況如表5所示:

表5
已知廠家每年年初有一次濾芯促銷活動,促銷期內每個濾芯售價1千元,促銷期結束后每個濾芯恢復原價2千元。該場館每年年初先在促銷期購買n(n≥8,且n∈N*)個濾芯,如果不夠用,則根據需要按原價購買補充。試問:該場館年初促銷期購買多少個濾芯,使當年購買濾芯的總花費最合理? 請說明理由。(不考慮往年剩余濾芯和下一年需求)
解析:(1)由題得125×15+175×6)=115。
(2)一個月30天中達到優或良的天數為9,空氣質量等級達到優或良的概率為,所以未來一周(7 天)中該場館至少有兩天空氣質量達到優或良的概率為0.3×0.76-0.77≈0.67。
(3)按照這個數據,每年需要6 到10 個濾芯,也就是n=8,9,10,假設需要為Z,則P(Z=10)=0.5×0.5=0.25,P(Z=9)=0.5×0.3×2=0.3,P(Z≤8)=1-0.25-0.3=0.45,那么當n=8 時,會有花費Cn=8的分布為P(Cn=8=1 000n)=P(Z≤8)=0.45,P(Cn=8=1 000n+2 000)=P(Z=9)=0.3,P(Cn=8=1 000n+4 000)=P(Z=10)=0.25,均值E(Cn=8)=0.45×8 000+0.3×10 000+0.25×12 000=9 600,同理算出E(Cn=9)=(0.45+0.3)×9 000+0.25×11 000=9 500,E(Cn=10)=10 000,故買9個最劃算。
點評:依據概率與統計學中的方法對數據進行分析,作出合理的決策,考查了數據分析素養和創新應用意識。設問的開放性、答題的多樣性,以及根據統計的意義作決策是本題的亮點。
概率統計模塊的解答題更加貼近生活實際,以實際應用情境來設置相應問題,同時情境更加接近于同學們的日常生活,數學應用模型更加合理與科學,注重數學內部知識的有機融合與交匯等。

