含能材料自催化分解特性的快速鑒別方法

平川， 甘強(qiáng)， 張蕊， 都振華， 馮長(zhǎng)根

(1.北京理工大學(xué) 爆炸科學(xué)與技術(shù)國(guó)家重點(diǎn)實(shí)驗(yàn)室， 北京 100081； 2.西安航天化學(xué)動(dòng)力有限公司， 陜西 西安 710025；3.陜西應(yīng)用物理化學(xué)研究所 應(yīng)用物理化學(xué)重點(diǎn)實(shí)驗(yàn)室， 陜西 西安 710061)

0 引言

自催化反應(yīng)是指分解產(chǎn)物在反應(yīng)過(guò)程中充當(dāng)催化劑的一種反應(yīng)類型[1]，這類反應(yīng)在含能材料的熱分解過(guò)程中很常見(jiàn)[2-5]。自催化分解反應(yīng)通常伴隨著熱量的突然釋放，因此這類反應(yīng)往往非常危險(xiǎn)且難以預(yù)測(cè)。含能材料的自催化分解現(xiàn)象在發(fā)生劇烈反應(yīng)(燃燒或熱爆炸)之前，很長(zhǎng)一段時(shí)間都不會(huì)有明顯的溫升現(xiàn)象，一旦產(chǎn)生明顯的溫升就會(huì)迅速成長(zhǎng)為燃燒或熱爆炸[6]，因此如何快速準(zhǔn)確地鑒別自催化反應(yīng)并判斷自催化反應(yīng)強(qiáng)度，一直是研究的熱點(diǎn)和難點(diǎn)[7-9]。

在以往的研究中，往往將具有自催化特性的物質(zhì)按照n級(jí)反應(yīng)進(jìn)行動(dòng)力學(xué)計(jì)算分析[10-12]，但會(huì)造成危險(xiǎn)性評(píng)估的偏差。為準(zhǔn)確描述物質(zhì)的自催化反應(yīng)，1944年P(guān)rout等[13]提出Prout-Tompkins反應(yīng)模型，描述了高錳酸鉀的自催化熱分解過(guò)程。1994年Dien等[14]基于Prout-Tompkins模型提出了通用性更強(qiáng)的Benito-Perez反應(yīng)模型，并給出了判斷自催化反應(yīng)強(qiáng)弱的依據(jù)。后續(xù)的Kamal-Sourour反應(yīng)模型[15]、Avrami-Erofeev反應(yīng)模型[16-19]等都是基于以上兩種反應(yīng)模型的改進(jìn)，以上自催化反應(yīng)模型的提出對(duì)于研究自催化反應(yīng)的進(jìn)程提供了有利條件。

表1給出了常見(jiàn)自催化反應(yīng)動(dòng)力學(xué)模型的機(jī)理函數(shù)表達(dá)式。需要特別指出的是，機(jī)理函數(shù)是定量描述反應(yīng)速率隨反應(yīng)進(jìn)度α變化關(guān)系的函數(shù)，并無(wú)分布函數(shù)特性。

1987年Keenan[20]提出了利用差示掃描量熱儀(DSC)或微熱量熱儀(C80)鑒別自催化反應(yīng)的等溫測(cè)量方法，通過(guò)測(cè)量反應(yīng)放熱速率曲線可靠鑒別自催化反應(yīng)。2002年Leila等[21]利用1階動(dòng)力學(xué)反應(yīng)模型擬合計(jì)算出物質(zhì)在初始分解階段的反應(yīng)活化能，認(rèn)為高于220 kJ/mol的物質(zhì)反應(yīng)類型均為自催化反應(yīng)。Malek[22]、Gotor等[23]、Sbirrazzuoli等[24]均提出了基于DSC的自催化反應(yīng)鑒定方法，但此種方法的起始計(jì)量溫度難以確定，起始溫度過(guò)高或過(guò)低均會(huì)對(duì)試驗(yàn)結(jié)果產(chǎn)生較大誤差，影響自催化反應(yīng)的判定。2013年Roduit等[25]研究了初始轉(zhuǎn)換率對(duì)自催化反應(yīng)進(jìn)程的影響。2014年Yang等[26]基于Roduit的研究提出了“中斷回掃法”鑒別自催化反應(yīng)。2016年Wang等[27]利用中斷回掃法完成了部分含能材料自催化反應(yīng)的準(zhǔn)確鑒別，但該方法需要進(jìn)行多次測(cè)量，測(cè)試過(guò)程較為繁瑣。

表1 常見(jiàn)的固體自催化反應(yīng)機(jī)理函數(shù)Table 1 Common autocatalytic reaction mechanism functions for solid

21世紀(jì)以來(lái)，絕熱加速量熱儀(ARC)等被大量應(yīng)用于含能材料的熱分解動(dòng)力學(xué)研究中[28-30]。與DSC相比，ARC可以進(jìn)行更大樣品量的試驗(yàn)，更接近物質(zhì)反應(yīng)的真實(shí)環(huán)境。2018年Dong等[31]利用ARC對(duì)危險(xiǎn)物質(zhì)的自催化反應(yīng)強(qiáng)度等級(jí)進(jìn)行了分類，該方法需要準(zhǔn)確計(jì)算熱動(dòng)力學(xué)參數(shù)。2020年Zhao等[32]提出了無(wú)需計(jì)算動(dòng)力學(xué)參數(shù)的絕熱環(huán)境自催化反應(yīng)鑒別方法，拓展了絕熱設(shè)備在自催化反應(yīng)研究方面的應(yīng)用，但該方法需要對(duì)物質(zhì)進(jìn)行完整的放熱試驗(yàn)，對(duì)于含能材料的試驗(yàn)極有可能造成嚴(yán)重的爆炸事故和精密儀器的損壞。

本文基于絕熱量熱法，提出一種在自催化反應(yīng)初期即可完成自催化反應(yīng)鑒別的方法，并可根據(jù)特征信號(hào)判斷自催化反應(yīng)強(qiáng)度。該方法能夠避免含能材料測(cè)量過(guò)程中的熱爆炸現(xiàn)象發(fā)生，同時(shí)快速準(zhǔn)確地鑒別出含能材料熱分解反應(yīng)類型，并判斷自催化特性強(qiáng)度。

1 鑒別方法的原理分析

1.1 理論依據(jù)

表1所示機(jī)理函數(shù)f(α)體現(xiàn)了反應(yīng)速率與反應(yīng)物(部分包括產(chǎn)物)物質(zhì)的量的相關(guān)性。由于遵循不同的反應(yīng)機(jī)理，在反應(yīng)物轉(zhuǎn)化率發(fā)生變化時(shí)，絕熱反應(yīng)體系的反應(yīng)速率必然會(huì)有不同變化。為量化這種變化，選取5種常見(jiàn)的機(jī)理函數(shù)(1級(jí)反應(yīng)，2級(jí)反應(yīng)，P-T反應(yīng)，A-E反應(yīng)，Cnm反應(yīng))，為模擬真實(shí)的分解反應(yīng)，以α1=0.06為初始計(jì)算點(diǎn)，計(jì)算機(jī)理函數(shù)隨轉(zhuǎn)化率變化的比值f(αn)/f(α1)，結(jié)果如圖1所示。

圖1 不同機(jī)理函數(shù)f(αn)/f(α1)隨轉(zhuǎn)化率α變化的計(jì)算結(jié)果Fig.1 Calculation of different mechanism functions f(αn)/f(α1) with the conversion rate α

由圖1可見(jiàn)，與n級(jí)反應(yīng)相比，自催化反應(yīng)(P-T反應(yīng)、A-E反應(yīng)、Cnm反應(yīng))的f(αn)/f(α1)值會(huì)隨著轉(zhuǎn)化率的增大迅速升高，且存在最大值，到達(dá)最大值后比值進(jìn)入下降區(qū)間，轉(zhuǎn)換率接近1時(shí)f(αn)/f(α1)值無(wú)限逼近于0。在上升區(qū)間內(nèi)自催化反應(yīng)的f(αn)/f(α1)初始值始終大于1。而n級(jí)反應(yīng)的f(αn)/f(α1)始終在1以下。利用這種差異可以鑒別熱分解反應(yīng)的反應(yīng)類型。

針對(duì)不同的反應(yīng)機(jī)理，都有特定的機(jī)理函數(shù)f(α)所決定的特性形狀，這會(huì)體現(xiàn)到反應(yīng)體系的反應(yīng)速率中。反應(yīng)體系的反應(yīng)速率一般可表示為

(1)

由圖1可以看出，f(αn)/f(α1)比值越高，該機(jī)理函數(shù)的數(shù)值增長(zhǎng)速度越快，反應(yīng)自催化特性也就越強(qiáng)，反應(yīng)越不容易得到控制，因此f(αn)/f(α1)能夠較好地量化自催化反應(yīng)機(jī)理函數(shù)f(α)的“加速特性”(自催化特性)。此結(jié)論對(duì)具有自催化特性物質(zhì)的鑒別和自催化反應(yīng)強(qiáng)度分類具有重要意義。

1.2 鑒別方法的公式推導(dǎo)

理想絕熱條件下，反應(yīng)物分解放出的熱量全部用于自身溫度的提升，由熱力學(xué)第一定律可知，在絕熱放熱反應(yīng)體系下存在：

dQ=Q∞×dα=cp×m×φ×dT

(2)

式中：dQ為任一時(shí)間段內(nèi)反應(yīng)體系的放熱量；Q∞為反應(yīng)總放熱量；dα為任一時(shí)刻反應(yīng)物的轉(zhuǎn)化率；cp為反應(yīng)物的比熱容，理想絕熱條件下反應(yīng)體系壓強(qiáng)不變，因此選用cp為反應(yīng)物的定壓比熱容；m為反應(yīng)物的比熱容和反應(yīng)物質(zhì)量；φ為絕熱反應(yīng)體系的熱慣性系數(shù)，理想狀態(tài)下其值為1；dT為任一時(shí)刻反應(yīng)體系的絕熱溫升。

假設(shè)cp不隨溫度的變化而變化，令c=cpmφ/Q∞，對(duì)于任一確定的反應(yīng)物，c為常數(shù)，有

(3)

式中：dt為轉(zhuǎn)化率由α1變化至αn所用的時(shí)間。根據(jù)阿倫尼烏斯定律，有

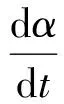
(4)

對(duì)于同一種反應(yīng)物，在不同的轉(zhuǎn)化率變化區(qū)間內(nèi)，有

(5)

(6)

式中：T1、T2分別為不同轉(zhuǎn)化率對(duì)應(yīng)的溫度。

令Δt1=Δt2，式(5)與式(6)相除，可得

(7)

結(jié)合式(3)可得

(8)

式(8)的意義在于，在已知反應(yīng)物絕熱放熱反應(yīng)過(guò)程中的活化能Ea和任意兩時(shí)刻反應(yīng)體系溫度及兩時(shí)刻對(duì)應(yīng)的溫度變化速率后，即可獲得機(jī)理函數(shù)隨轉(zhuǎn)化率變化的比值f(αn)/f(α1)。根據(jù)比值f(αn)/f(α1)即可完成自催化反應(yīng)以及反應(yīng)強(qiáng)度的判斷。通過(guò)ARC進(jìn)行的絕熱量熱試驗(yàn)往往很難獲得物質(zhì)精確的Ea，但在f(αn)/f(α1)的計(jì)算過(guò)程中，Ea往往對(duì)反應(yīng)結(jié)果的判斷沒(méi)有較大影響，此結(jié)論在本文第3節(jié)會(huì)有詳細(xì)闡述。為更好地驗(yàn)證公式推導(dǎo)的正確性，本文采用數(shù)值模擬方法對(duì)鑒別方法進(jìn)行驗(yàn)證。

2 絕熱體系分解反應(yīng)模型建立與計(jì)算分析

2.1 絕熱體系分解反應(yīng)模型的建立

參考Zhao等[32]的研究成果，建立對(duì)于絕熱反應(yīng)體系的放熱量關(guān)系式如下：

(9)

式中：Tf為反應(yīng)終止溫度；Ton為反應(yīng)初始放熱溫度；Q0為反應(yīng)初始放熱量；α0為初始轉(zhuǎn)化率。

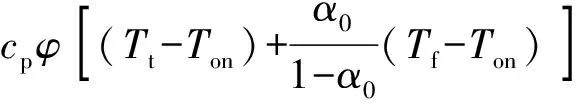
(10)

(11)

式中：Qt、Tt和αt分別為t時(shí)刻反應(yīng)放熱量、反應(yīng)溫度和轉(zhuǎn)化率。由式(11)可得

(12)

根據(jù)阿倫尼烏斯定律，有

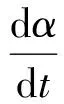
(13)

(14)

由此可得4種常見(jiàn)反應(yīng)類型的dT/dt的表達(dá)式，如表2所示。

由表2可知，根據(jù)式(11)、式(12)以及反應(yīng)機(jī)理函數(shù)f(α)，在已知反應(yīng)體系總放熱量Q∞和反應(yīng)初始放熱溫度Ton的情況下，即可完成不同反應(yīng)機(jī)理下絕熱量熱試驗(yàn)過(guò)程的模擬計(jì)算。

2.2 數(shù)值計(jì)算分析

首先計(jì)算φ=1時(shí)1級(jí)反應(yīng)、2級(jí)反應(yīng)、P-T反應(yīng)、Cnm反應(yīng)和A-E反應(yīng)的dT/dt與T之間的關(guān)系，如圖2所示。數(shù)值計(jì)算中用到的參數(shù)如表3所示。由圖2和表3可以看出，P-T、A-E反應(yīng)和Cnm反應(yīng)的放熱速率普遍高于1級(jí)反應(yīng)和2級(jí)反應(yīng)。

表2 4種常見(jiàn)反應(yīng)類型的dT/dt的表達(dá)式Table 2 Expressions for dT/dt for several common reaction types

圖2 φ=1時(shí)dT/dt隨T變化Fig.2 dT/dt varies with T for φ=1

表3 仿真計(jì)算參數(shù)Table 3 Parameters used in the simulations

圖3 不同熱慣性下5種反應(yīng)機(jī)理的dT/dt隨α變化Fig.3 Variation of dT/dt with α for five reaction mechanisms with different thermal inertia

計(jì)算φ取值分別為1、2、3、4、5、6時(shí)1級(jí)反應(yīng)、2級(jí)反應(yīng)、P-T反應(yīng)、Cnm反應(yīng)和A-E反應(yīng)的dT/dt與轉(zhuǎn)化率α之間的關(guān)系，如圖3所示。由于絕熱量熱儀的實(shí)際初始采樣值為0.02 ℃/min，將模擬計(jì)算時(shí)的dT/dt起始計(jì)算點(diǎn)α0也設(shè)置在0.02 ℃/min所對(duì)應(yīng)的轉(zhuǎn)化率。

由圖3可見(jiàn)，當(dāng)熱慣性系數(shù)過(guò)大時(shí)(如φ=6)，2級(jí)反應(yīng)出現(xiàn)了檢測(cè)不到放熱信號(hào)(反應(yīng)體系的放熱速率始終小于0.02 ℃/min)的情況。表2中dT/dt與熱慣性系數(shù)呈反比。由式(2)可見(jiàn)，反應(yīng)體系的絕熱溫升與熱慣性系數(shù)有直接關(guān)系，熱慣性系數(shù)越大，反應(yīng)的絕熱溫升越小。式(11)表明了反應(yīng)體系的絕熱溫升直接影響反應(yīng)體系的實(shí)時(shí)轉(zhuǎn)化率，對(duì)于熱慣性系數(shù)大的反應(yīng)體系，每升高1 ℃對(duì)應(yīng)反應(yīng)體系的轉(zhuǎn)化率增量也就越大，從而解釋了熱慣性過(guò)大時(shí)檢測(cè)不到放熱信號(hào)的現(xiàn)象。因此熱慣性過(guò)大時(shí)(如圖3中φ取值為5、6)，可檢測(cè)到放熱信號(hào)時(shí)反應(yīng)體系轉(zhuǎn)化率達(dá)到了一個(gè)較高的值，進(jìn)入了圖1所示轉(zhuǎn)化率α下降區(qū)間內(nèi)，造成了dT/dt隨轉(zhuǎn)化率的增加而降低。

圖4所示為熱慣性對(duì)4種反應(yīng)機(jī)理函數(shù)初始轉(zhuǎn)化率的影響規(guī)律。由圖4可見(jiàn)，熱慣性越大，起始考察點(diǎn)對(duì)應(yīng)的起始轉(zhuǎn)化率也越大，這是因?yàn)闊釕T性越大，樣品容器升溫所需熱量占總放熱量比例也就越大，導(dǎo)致反應(yīng)體系的升溫速率下降，絕熱溫升降低，進(jìn)而會(huì)出現(xiàn)起始考察點(diǎn)的放熱信號(hào)出現(xiàn)“滯后”的現(xiàn)象。對(duì)比可見(jiàn)，Cnm自催化反應(yīng)受熱慣性影響較小，A-E反應(yīng)和P-T反應(yīng)次之，2級(jí)反應(yīng)受熱慣性影響最大。

圖4 熱慣性對(duì)4種反應(yīng)機(jī)理函數(shù)初始轉(zhuǎn)化率的影響Fig.4 Effect of thermal inertia on the initial conversion rate of the four reaction mechanism functions

圖5 不同熱慣性下5種反應(yīng)機(jī)理函數(shù)隨α變化Fig.5 Variation of the five reaction mechanism functions with α for different thermal inertia

圖5為根據(jù)仿真結(jié)果計(jì)算出的不同反應(yīng)機(jī)理函數(shù)和熱慣性系數(shù)下的f(αn)/f(α1)值。由圖5可見(jiàn)，無(wú)論是n級(jí)反應(yīng)還是自催化反應(yīng)，在轉(zhuǎn)化率接近1時(shí)f(αn)/f(α1)值均無(wú)限接近于0；但n級(jí)反應(yīng)的f(αn)/f(α1)值從初始值1開(kāi)始單調(diào)遞減，自催化反應(yīng)的f(αn)/f(α1)值從初始值1開(kāi)始逐漸上升，到達(dá)一個(gè)峰值后再逐漸下降至0。

表4給出了數(shù)值模擬中5種反應(yīng)機(jī)理函數(shù)不同熱慣性系數(shù)下的f(αn)/f(α1)最大值。由表4可見(jiàn)，無(wú)論哪種熱慣性系數(shù)條件下，f(αn)/f(α1)值的大小排序均為Cnm>P-T>A-E，表明3種自催化反應(yīng)機(jī)理函數(shù)的自催化特性強(qiáng)度排序?yàn)镃nm>P-T>A-E。

表4 模擬計(jì)算自催化機(jī)理函數(shù)的 f(αn)/f(α1)最大值Table 4 Calculated maximum value of f(αn)/f(α1) by the autocatalytic mechanism function

在部分較大的熱慣性系數(shù)計(jì)算條件下，自催化反應(yīng)機(jī)理函數(shù)的f(αn)/f(α1)初始值在1以下，這是因?yàn)闊釕T性系數(shù)過(guò)大導(dǎo)致出現(xiàn)初始放熱信號(hào)時(shí)反應(yīng)體系的轉(zhuǎn)化率在機(jī)理函數(shù)數(shù)值的下降區(qū)間內(nèi)。因此，在實(shí)際測(cè)量過(guò)程中應(yīng)適當(dāng)增加樣品量以減小熱慣性，避免起始特征信號(hào)出現(xiàn)在圖5中機(jī)理函數(shù)數(shù)值的下降區(qū)間內(nèi)。

3 含能材料的絕熱量熱試驗(yàn)與結(jié)果分析

3.1 試驗(yàn)樣品

DTBP與甲苯的混合物在放熱過(guò)程中嚴(yán)格遵循1級(jí)反應(yīng)模型[31]，因此選取20%DTBP與甲苯的混合溶液、超細(xì)HNS-Ⅳ、BNCP、CL-20、CMC-LA 5種樣品進(jìn)行絕熱量熱試驗(yàn)。本文試驗(yàn)所用20%DTBP與甲苯混合溶液為分析純99.99%，超細(xì)HNS-Ⅳ粉體粒度分布為0.2～20 μm，與普通粒徑HNS-Ⅳ相比，超細(xì)HNS-Ⅳ放熱反應(yīng)更為劇烈，反應(yīng)特征信號(hào)更易辨別[33]。以上材料均為實(shí)驗(yàn)室自制，純度超過(guò)99%。

3.2 試驗(yàn)條件

利用德國(guó)耐馳儀器公司ARC254型絕熱加速量熱儀對(duì)樣品進(jìn)行初始放熱階段的測(cè)量。為精確測(cè)量樣品的放熱信號(hào)，選用H-W-S模式，靈敏度為0.02 ℃/min，升溫速率2 ℃/min，升溫臺(tái)階5 ℃。測(cè)試樣品容器選用耐馳NIB010816型Ti質(zhì)樣品球。為防止樣品發(fā)生劇烈的放熱反應(yīng)，放熱溫度緊急停止閾值設(shè)置為1.0 ℃/min。

3.3 絕熱量熱試驗(yàn)結(jié)果

考察以上5種材料從0.02 ℃/min～0.50 ℃/min的放熱過(guò)程溫度變化情況。為便于數(shù)據(jù)統(tǒng)一，將5種材料的起始放熱速率考察點(diǎn)設(shè)置為0.02 ℃/min，獲得20%DTBP與甲苯混合溶液、HNS-Ⅳ、BNCP、CL-20、CMC-LA熱分解初始階段放熱曲線如圖6所示。由圖6可見(jiàn)，初始分解溫度隨熱慣性系數(shù)的增加而升高，與圖5中的仿真計(jì)算結(jié)果一致。在放熱過(guò)程中，反應(yīng)溫度隨時(shí)間的增長(zhǎng)隨時(shí)間的增長(zhǎng)呈指數(shù)上升，表明0.02 ℃/min～0.50 ℃/min放熱過(guò)程中產(chǎn)物的熱分解均為增速反應(yīng)。

3.4 試驗(yàn)結(jié)果分析

根據(jù)圖6結(jié)果計(jì)算5種測(cè)試樣品的f(αn)/f(α1)值，結(jié)果如圖7所示，由于沒(méi)有準(zhǔn)確計(jì)算各樣品的活化能Ea，暫時(shí)將計(jì)算所需Ea統(tǒng)一設(shè)置為180 kJ/mol。為便于數(shù)據(jù)統(tǒng)一，將5種材料的初始采樣放熱速率設(shè)置在了0.02 ℃/min。

由圖7可以看出，隨著反應(yīng)溫度的升高，20%DTBP與甲苯混合溶液絕熱放熱反應(yīng)的f(αn)/f(α1)值自1開(kāi)始逐漸下降，表明20%DTBP與甲苯混合溶液的放熱反應(yīng)為n級(jí)反應(yīng)，與Dong等[31]分析結(jié)果一致。HNS-Ⅳ、BNCP、CL-20、CMC-LA的f(αn)/f(α1)計(jì)算值均在1以上，且該計(jì)算值隨著時(shí)間的增加而增加，表明以上4種含能材料的絕熱熱分解過(guò)程均為自催化反應(yīng)，與Lee等[34]、周建華等[35]、王凱等[36]和劉劍超等[37]的研究結(jié)果一致。根據(jù)各個(gè)樣品計(jì)算結(jié)果可見(jiàn)，熱慣性越大，f(αn)/f(α1)的值越小，即自催化反應(yīng)的特征信號(hào)隨熱慣性系數(shù)的增大而降低，較大的熱慣性能夠降低自催化反應(yīng)的反應(yīng)強(qiáng)度。

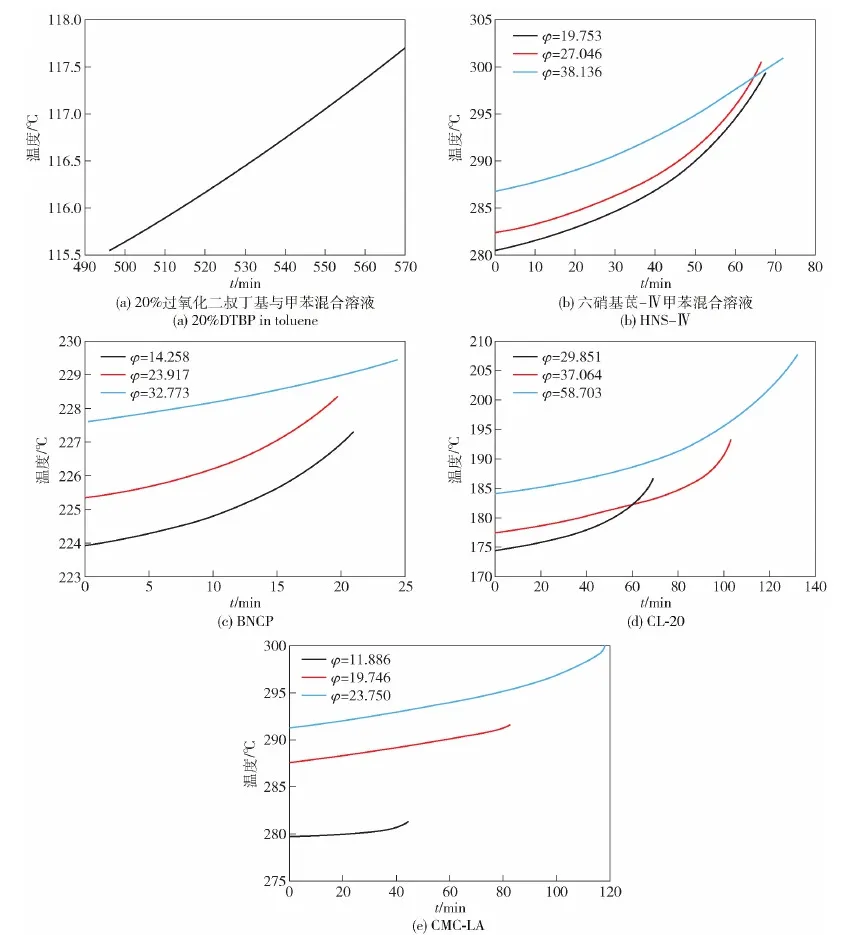
圖6 5種樣品的熱分解初始階段放熱曲線Fig.6 Exothermic curves for the initial stages of thermal decomposition of the five samples

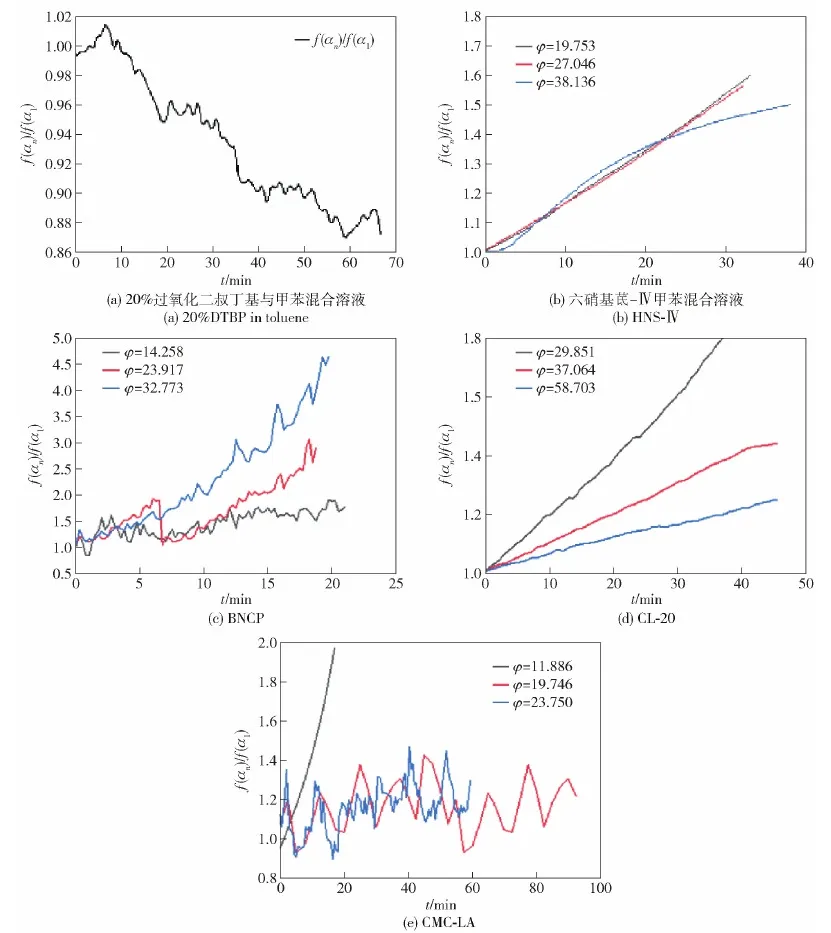
圖7 5種樣品的f(αn)/f(α1)計(jì)算值Fig.7 Calculated values of f(αn)/f(α1) for the five samples

為考察活化能Ea對(duì)f(αn)/f(α1)值的影響，將Ea分別取100 kJ/mol、150 kJ/mol、200 kJ/mol和250 kJ/mol，計(jì)算不同Ea時(shí)f(αn)/f(α1)值。表5 給出了f(αn)/f(α1)值的計(jì)算條件，其中不同活化能數(shù)值用/分隔開(kāi)。根據(jù)表5中的條件計(jì)算得出的f(αn)/f(α1)值見(jiàn)圖8。

由圖8可見(jiàn)，f(αn)/f(α1)計(jì)算值與活化能Ea值呈反比，Ea值越大，f(αn)/f(α1)計(jì)算值越小。但無(wú)論是n級(jí)反應(yīng)還是自催化反應(yīng)，Ea值均不影響f(αn)/f(α1)計(jì)算值隨時(shí)間變化的總體趨勢(shì)，即Ea取不同值時(shí)，n級(jí)反應(yīng)的f(αn)/f(α1)計(jì)算值仍為隨時(shí)間單調(diào)遞減，且計(jì)算值全部在1以內(nèi)，自催化反應(yīng)的f(αn)/f(α1)計(jì)算值仍為隨時(shí)間單調(diào)遞增，且計(jì)算值全部在1以上。這是因?yàn)榛罨蹺a值代表了反應(yīng)發(fā)生的難易程度，Ea值越大，反應(yīng)越難發(fā)生，反應(yīng)速率趨于平緩，表現(xiàn)在圖8中即為f(αn)/f(α1)值較小。機(jī)理函數(shù)f(α)代表了反應(yīng)進(jìn)行方式與反應(yīng)物消耗的相關(guān)性，Ea值雖能影響反應(yīng)速率卻不能影響反應(yīng)進(jìn)行方式的本質(zhì)，因此活化能Ea的取值不影響f(αn)/f(α1)計(jì)算值隨時(shí)間的整體變化趨勢(shì)，也不影響基于f(αn)/f(α1)計(jì)算值的反應(yīng)類型判斷。

4 結(jié)論

本文基于絕熱量熱法提出了可快速判斷物質(zhì)自催化分解特性和強(qiáng)度的方法，基于n級(jí)反應(yīng)和自催化反應(yīng)模型研究了熱慣性對(duì)機(jī)理函數(shù)隨時(shí)間變化率的比值f(αn)/f(α1)的影響規(guī)律，利用絕熱量熱法測(cè)量5種樣品并進(jìn)行自催化特性分析。得到如下主要結(jié)論：

1)仿真結(jié)果表明，3種自催化反應(yīng)機(jī)理函數(shù)的自催化特性強(qiáng)度排序?yàn)镃nm反應(yīng)>P-T反應(yīng)>A-E反應(yīng)，熱慣性系數(shù)深刻影響著物質(zhì)的絕熱放熱過(guò)程。熱慣性系數(shù)越大，物質(zhì)的放熱反應(yīng)強(qiáng)度越小，與此同時(shí)自催化反應(yīng)的特征信號(hào)越弱。

2)f(αn)/f(α1)計(jì)算值越高，表明該物質(zhì)分解自催化特性越強(qiáng)。計(jì)算表明，20%DTBP與甲苯混合溶液的絕熱熱分解反應(yīng)為n級(jí)反應(yīng)，HNS-Ⅳ、BNCP、CL-20和CMC-LA的絕熱放熱反應(yīng)為自催化反應(yīng)。

3)活化能Ea的值不影響f(αn)/f(α1)計(jì)算值隨反應(yīng)時(shí)間的走勢(shì)，也不影響基于f(αn)/f(α1)計(jì)算值判斷出的反應(yīng)類型結(jié)果。因此本文方法可迅速完成反應(yīng)類型的鑒別和自催化特性強(qiáng)度的判斷，相對(duì)于等溫法、中斷回掃法等方法可大大減少試驗(yàn)時(shí)間，并降低發(fā)生意外事故的危險(xiǎn)性，可靠性有待進(jìn)一步試驗(yàn)驗(yàn)證。

表5 f(αn)/f(α1)值的計(jì)算條件Table 5 Conditions for calculating the value of f(αn)/f(α1)

圖8 不同活化能下5種樣品f(αn)/f(α1)計(jì)算值Fig.8 Calculated values of f(αn)/f(α1) for the five samples at different activation energies