基于彈道彎曲角速度單矢量的制導炮彈滾轉角空中粗對準方法

楊啟帆， 王江， 范世鵬， 白嬋， 周永佳， 胡少勇

(1.北京理工大學 宇航學院， 北京 100081； 2.北京理工大學 中國- 阿聯酋智能無人系統“一帶一路”聯合實驗室， 北京 100081；3.西北工業集團有限公司， 陜西 西安 710043)

0 引言

精確制導炮彈在發射后通常會采取低速滾轉的飛行方案[1]，具有控制系統簡單、可有效對抗激光反導、改善質量偏心和軸系不對稱等優勢，得以廣泛應用[2]。為順應制導炮彈低成本、遠程化的發展趨勢，必須建立低成本導航系統。然而，制導炮彈內彈道呈現超高轉速、超大過載的特點，慣性導航系統無法進行初始對準。因此，必須在發射后的無控段對滾轉角進行快速空中粗對準，以便在滑翔段實施機動指令分解和組合導航精對準。

對于制導炮彈，無控段攻角與側滑角在很短時間內即可收斂于0°，可以通過衛星獲取的速度信息解算俯仰角和偏航角。然而，滾轉角很難獲得基準，如何實現滾轉角的空中對準，是當前制導炮彈的難點問題[3]。空中對準利用衛星、慣性制導(以下簡稱慣導)等組合系統的卡爾曼濾波技術得到更精確的彈體姿態，但必須進行輔助機動飛行。若在滾轉角快速時變且完全未知的條件下，制導炮彈控制系統無法完成空間指令分解，則輔助機動可能是空間中的任意方向，這是制導炮彈難以接受的。

利用地磁傳感器可以測量地磁場信息來獲取彈體姿態角[4-6]，抗過載能力強、誤差不隨時間累積，但受限于磁場測量精度并且要增加額外的硬件設備。為避免陀螺儀超量程及附加誤差大的問題[7]，無陀螺慣性系統用于在空中測量滾轉角，成本低、功耗小，但受限于加速度計的精度并存在計算量大的問題。近些年，衛星與慣導組合系統應用較廣泛，MEMS-GPS[8]組合系統的姿態對準方法應用于空中粗對準滾轉角，根據彈體轉動運動學方程解算滾轉角，但未考慮制導炮彈的姿態運動在實際飛行中特有的頻域特性，對慣性元件的誤差分析不足，僅針對較高精度、標定精確的慣導系統。佘浩平等[9]提出一種GPS-INS制導彈藥的空中粗對準滾轉角方法，但該方法利用GPS測量的速度信息求解彈道角，輸出頻率低、誤差較大，同樣未考慮彈體姿態運動的頻域特性帶來的誤差。Wu等[10-11]提出一種基于速度- 位置方程的積分算法，利用慣導、衛星組合系統對飛機進行空中姿態對準，但并未在制導炮彈領域應用。彭博等[12]提出一種基于速度匹配與機動輔助的滾轉角精對準方法，但需要提供機動控制參數，不適合在中制導前的無控段使用。

在慣導小型化、低成本的發展趨勢下，MEMS器件逐漸被廣泛應用于制導武器。然而，MEMS慣導由于慣性器件漂移大、安裝誤差標定困難，導致陀螺儀、加速度計的輸出誤差很大[13]。王思遠等[14]提出一種雙軸連續旋轉調制方法，補償了MEMS慣性器件的零偏、標度因子等誤差，但安裝構型復雜，不適合在滾轉體制的載體上應用。

針對上述問題，本文提出一種基于矢量定姿原理，利用單矢量即角速率陀螺敏感的彈體角速度，以近似彈道彎曲角速度矢量，在無控段實現滾轉角的粗對準。對比其他滾轉角空中對準算法，該方法巧妙地利用了制導炮彈低速滾轉特性，根據制導炮彈姿態運動的頻域特性處理中低精度的慣性元件誤差，不需要機動輔助，無需衛星信息，并減少地磁傳感器等元件的安裝，可在滿足粗對準精度要求的條件下降低成本、提高可靠性。

1 問題描述

制導炮彈在發射后，通過斜置尾翼或發動機噴管斜置，使彈體以一定角速率繞著縱軸旋轉。助推段結束后進行無控飛行，在彈體俯仰角滿足一定條件后，舵機啟控，進入慣導滑翔階段，最終進入末制導階段打擊目標。圖1為制導炮彈飛行全程彈道，炮彈飛行以北天東導航坐標系為參考。由于制導炮彈控制方式為單通道控制，需要獲取精確的滾轉角進行控制指令分解，另一方面，慣導的運行也需要精確的姿態初值，因此有必要在無控段進行滾轉角的對準。

本文所用的坐標系有導航坐標系OXnYnZn、彈體坐標系OXbYbZb、準彈體坐標系OXYZ、準速度坐標系OXvYvZv。選用北天東(NUE)作為導航坐標系，彈體坐標系定義為前、上、右方向。令θ表示彈道傾角，ψv表示彈道偏角，?、ψ、γ表示彈體坐標系與導航坐標系之間的轉動姿態角，分別表示俯仰角、偏航角、滾轉角。

建立導航坐標系與彈體坐標系的關系如圖2所示，平面OAB及OAC表示水平面和鉛垂面。準彈體坐標系與準速度坐標系的關系如圖3所示。圖3中，OABC平面代表飛行速度所在的鉛垂面，Xv軸表示炮彈速度矢量的方向，OCDE表示彈體縱軸所在的鉛垂面，稱之為射面。Yv、Y軸均在OCDE平面內，并分別與Xv、X軸垂直，準彈體坐標系可理解為不隨彈體滾轉的彈體坐標系。準速度坐標系的Yv軸與速度矢量所在鉛垂面OABC的夾角稱為速度傾斜角γv(見圖3)，表征速度矢量偏離彈體縱軸的程度。

圖2 導航坐標系與彈體坐標系的關系Fig.2 Relationship between navigation coordinate system and projectile coordinate system

圖3 準彈體坐標系與準速度坐標系的關系Fig.3 Relationship between quasi-projectile coordinate system and quasi-velocity coordinate system

彈體繞質心轉動的運動學方程[16]為

(1)

由式(1)的前兩式解得

(2)

由于無控段偏航角速率近似為0°/s，則簡化式(2)為

(3)

(4)

2 滾轉角粗對準方法

2.1 無控段角速率陀螺信息頻域分析

由式(3)可知，理論上，制導炮彈在無控段飛行過程中，安裝在彈體坐標系y軸、z軸上的陀螺測量值是幅值為俯仰角速率的周期信號。但在制導炮彈實際飛行過程中，陀螺儀誤差不僅具有零偏及隨機噪聲，而且存在更多復雜的誤差項。制導炮彈的姿態運動具有特定的頻域特性，反映在陀螺儀測量數據中。一般地，陀螺儀數據有如下3種較明顯的頻域分量。

1)由于陀螺儀安裝軸偏角，y軸、z軸陀螺儀會引入滾轉角速率的信息，即使進行標定，在小誤差角條件下仍然會有較大的滾轉角速率分量。由于滾轉角速率變化較慢，該信息為低頻分量；陀螺儀存在零偏誤差，該誤差為低頻分量。

2)彈體滾轉引起的周期性信號，該分量反映無控段俯仰角速度的信息，是在無干擾、陀螺儀無誤差條件下的理論值。

3)根據導彈飛行力學原理，彈體在飛行過程中受到偶然干擾而產生附加攻角，在穩定力矩作用下彈體以一定頻率振蕩，稱之為特征頻率，與彈體滾轉頻率相關[17-18]。理論上彈體俯仰角與彈道傾角相等，但彈體在干擾下受到縱向擾動，若彈體是動態穩定的，則會存在振幅為Δ?、振蕩特征頻率為ωc的擺動。假設振幅在短時間內不變，彈體的俯仰角及俯仰角速度可表示為

(5)

則陀螺儀測量值變為

(6)

根據積化和差公式，可變形為

(7)

由式(7)可知，存在縱向擾動的情況下，角速率陀螺的測量值除滾轉頻率分量外，還包含如下頻域分量：

(8)

2.2 基于單矢量定姿的滾轉角粗對準

根據導彈飛行動力學公式，彈道傾角微分方程可表示為

(9)

在無控段彈道，制導炮彈的攻角及側滑角快速收斂為0°，即準彈體坐標系的縱軸X與準速度坐標系的縱軸Xv重合，速度傾斜角γv近似為0°。

?≈θ,ψ≈ψv,γv≈0°

(10)

無控段彈道傾角微分方程可簡化為

(11)

無控段彈體在重力作用下產生彈道傾角速度，本文稱為彈道彎曲角速度，其在慣性空間內可近似視為恒定方向的矢量。在彈體滾轉過程中，俯仰角速度被滾轉角信息調制，角速率陀螺可以測得俯仰角速度在彈體坐標系下的分量，由于攻角幾乎為0°，可以將彈體俯仰角速度近似為彈道彎曲角速度。

圖4為準彈體坐標系與彈體坐標系之間的關系，二者之間由滾轉角聯系起來。

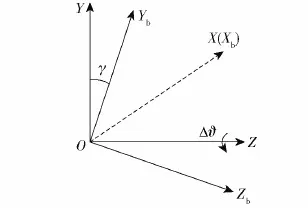
圖4 準彈體坐標系與彈體坐標系的關系Fig.4 The relation between quasi-projectile coordinate system and projectile coordinate system

根據制導炮彈的繞質心轉動的運動學方程可得到彈體姿態角速度的表達形式

(12)

式中：ωX、ωY、ωZ表示彈體姿態的角速度在準彈體坐標系的投影。制導炮彈的俯仰角速度矢量始終在準彈體坐標系的z軸上，即始終垂直與射面，則一段時間彈體俯仰角的變化Δ?也在該軸上，該矢量大小為負。本文方法將一段時間的俯仰角變化量投影至在起始時刻凍結的彈體坐標系下，從而實現滾轉角的對準。圖5為初始滾轉角對準方法示意圖。

圖5 初始滾轉角對準算法示意圖Fig.5 Schematic diagram of initial roll angle alignment algorithm

(13)

式中：

(14)

(15)

兩邊積分可得

(16)

展開得

(17)

(18)

(19)

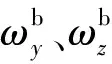
(20)

則滾轉角速率可通過滾轉軸的陀螺儀測量值近似，Δγ為當前時刻的彈體坐標系b(t)相對于初始彈體坐標系b(0)已滾過的滾轉角，可通過滾轉角速率測量值積分獲得。Δ?y表示一段時間俯仰角變化量在初始彈體坐標系y軸的投影，Δ?z表示一段時間俯仰角變化量在初始彈體坐標系z軸的投影。

在線對準滾轉角需要對離散陀螺儀數據數值積分。設定積分時間為t，N為采樣點，T為積分周期，

t=N×T

(21)

設定k代表第k個積分區間，

(22)

積分區間內已滾過的滾轉角可視為常值，計算方式如式(23)：

(23)

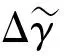
(24)

同理可得

(25)

定義滾轉角取值范圍γ∈[-180°,180°]，求得俯仰角變化量之后，通過Δ?y、Δ?z的符號進行滾轉角象限判斷，判斷依據如表1所示。

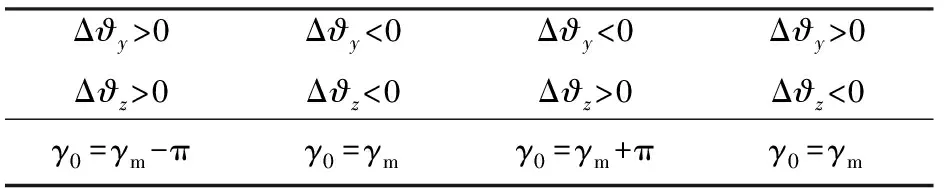
表1 象限判斷規則Table 1 Quadrant judgment rule

3 仿真與飛行試驗驗證

3.1 制導炮彈無控段滾轉角對準數學仿真

3.1.1 仿真條件

對制導炮彈進行無控段飛行仿真，設定初始飛行速度230 m/s，彈道傾角10°，滾轉角速率1 900°/s，初始滾轉角0°，陀螺儀輸出頻率100 Hz。理論上安裝在y軸、z軸的陀螺儀測量值是以俯仰角速率為幅值的周期信號。為模擬實際飛行條件，對輸出的陀螺儀數據添加誤差，由于MEMS陀螺在無控段啟動，在啟動初期零偏及量化噪聲尤其是低頻閃爍噪聲為主要誤差源[19]。在陀螺儀測量值經過帶通濾波器處理后，理論上僅存彈體轉速頻段的隨機噪聲，故簡化陀螺儀誤差模型如下。假設在該段時間彈體受到幅值為1°、頻率為2.5 Hz的縱向擾動；由于安裝誤差標定不完全，x軸陀螺儀信息在y軸、z軸上分別有0.5°、-0.25°的軸偏角投影；陀螺儀三軸存在標準差為0.25°/s的隨機白噪聲誤差及0.25°/s的零偏誤差。仿真構造的雙軸陀螺儀數據如圖6所示。

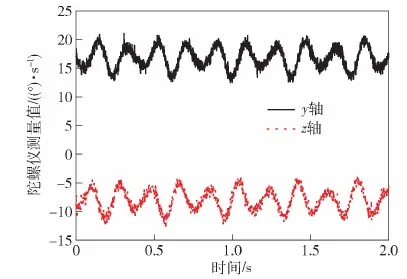
圖6 仿真陀螺儀測量值Fig.6 Simulation of gyroscope measurement

仿真得到的陀螺儀測量值具有多種誤差，首先對陀螺儀數據進行頻譜變換，角速率信號的頻域特性如圖7所示。由圖7可知，彈體姿態運動存在3種頻域分量，與理論分析相符。若要應用滾轉角對準方法，則需要利用FIR數字帶通濾波器提取陀螺儀測量值中與滾轉頻率有關的分量。

圖7 陀螺儀測量值頻譜圖Fig.7 Spectrum diagram of gyroscope measurement

3.1.2 滾轉角對準方法仿真驗證

選取3～7 s的陀螺儀數據，并提取與彈體滾轉頻率相關的分量，結果如圖8所示。

圖8 頻域處理后的陀螺儀測量值Fig.8 Gyroscope measurement processed in frequency domain

根據數字濾波器的窗函數截取特性[20]，濾波后的一段數據在端點處會出現幅值衰減至0的現象。因此，在方法實際應用時需要將端點附近的數據舍去。

由式(3)可得

(26)

通過頻域處理后的陀螺儀數據可計算彈道彎曲角速度大小，為驗證對彈道彎曲角速度重構的有效性，將彈道彎曲角速度處理結果與理論值進行對比，結果如圖9所示。通過對陀螺儀原始數據進行頻域處理，可以對彈道彎曲角速度進行重構，并保持良好的精度，便于應用于滾轉角對準。

圖9 彈道彎曲角速度重構效果Fig.9 Reconstruction effect of trajectory bending angular velocity

得到經過頻域處理的陀螺儀數據后，由式(4)可知，根據運動學公式，可利用某一時刻的y軸、z軸陀螺儀數據直接計算當前時刻滾轉角。而制導炮彈在實際飛行過程中，陀螺儀測量值存在著分布在各頻段的隨機噪聲，該誤差難以通過頻域處理全部分離。理論上采用積分策略會對隨機噪聲有平滑作用。仿真條件不變，對比兩種滾轉角對準方法的精度，計算4～5 s的滾轉角并與理論值對比，結果如圖10所示。

圖10 兩種對準方法的誤差對比Fig.10 Error comparison of the two alignment methods

對比利用運動學公式直接計算滾轉角的方法，本文提出的積分策略對準滾轉角對隨機噪聲有平滑作用，在陀螺儀存在多項誤差的情況下精度及可靠性較高，無明顯振蕩，對準精度保持在0.5°以內。

其他條件不變，假設陀螺儀測量值不存在白噪聲，選取滾轉通道陀螺零偏為0.25°/s、0.5°/s、0.75°/s 3種情況進行仿真分析，不同零偏條件下滾轉角對準誤差曲線如圖11所示。

圖11 陀螺儀零偏對滾轉角對準精度的影響Fig.11 Effect of gyroscope bias on roll Angle alignment accuracy

其他條件不變，假設陀螺儀測量值不存在零偏，設定陀螺儀分別存在標準差為0.25°/s、0.5°/s、0.75°/s的白噪聲的3種情況進行仿真分析，不同強度白噪聲條件下滾轉角對準誤差曲線如圖12所示。

圖12 陀螺儀白噪聲對對準精度的影響Fig.12 Effect of white noise of gyroscope on alignment accuracy

從圖11和圖12中可以看出，滾轉通道陀螺儀零偏會在一定程度上影響對準精度，但不會隨零偏的增大而發散，依然可以將精度控制在1°以內；陀螺儀測量值的白噪聲強度會影響對準的穩定性，在白噪聲較大的條件下，不同時刻的對準精度會有1°左右的波動。

3.2 飛行試驗驗證

將MEMS角速率陀螺搭載于某型號制導炮彈控制艙，對本文提出的粗對準方法進行飛行試驗驗證，實物圖如圖13所示。

圖13 實物圖Fig.13 Picture of real products

角速率陀螺輸出頻率為100 Hz，零偏指標為20°/h，搭載試驗未完全標定軸偏角誤差，由于所應用的制導炮彈射程在30 km以內，其工作時間較短，誤差影響較小，在飛行試驗中無需在線校正。在制導炮彈發射后35 s之前處于無控段，35 s開始中制導啟控。

該制導炮彈臨時裝有空間定向陀螺，為此次試驗提供滾轉基準，其結構如圖14(a)所示。定向陀螺在最高點解鎖后，彈軸與陀螺軸之間的夾角?g逐漸增大，外框架角αo隨滾轉角產生周期性變化，如圖14(b)所示。

圖14 空間定向陀螺示意圖Fig.14 Schematic diagram of gyroscope for spatial orientation

由圖14可知，當且僅當外框架角≥5°時，與外框架角固連的電位計信號將輸出5°片信號，其出現的中心時刻則為滾轉角為0°。利用空間定向陀螺可得到滾轉角，可對本文提出的滾轉角對準方法進行誤差分析。選取30～34 s內的陀螺測量數據，飛行試驗彈載記錄儀的角速率陀螺測量數據如圖15所示。

圖15 某型號制導炮彈的陀螺儀測量值Fig.15 Gyroscope measurement of a certain type of guided missile

在制導炮彈實際飛行中，陀螺儀測量值總體趨勢與仿真結果一致。對陀螺儀測量值進行頻譜分析，如圖16所示。

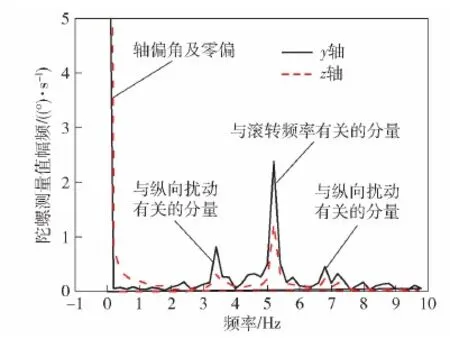
圖16 飛行試驗陀螺儀測量值頻譜圖Fig.16 Spectrum diagram of gyroscope measurement in flight test

在實際飛行條件下，陀螺儀數據除了存在已知的3種頻段外，在全頻段存在強度較大的隨機噪聲，利用帶通數字濾波器提取與彈體滾轉頻率相關的分量。依據帶通濾波器通帶設計原則，對本文飛行試驗設計的帶通濾波器進行分析。在30～34 s內，測得滾轉頻率在5.2～5.4 Hz之間，根據彈體設計的特征頻率2 Hz，求得通帶為[3.2 Hz,7.4 Hz]，該濾波器的特性如圖17所示。該濾波器可使滾轉頻率區間的信息完全通過，低頻段分量衰減至-40 dB以下，滿足彈道彎曲角速度重構的需求。

圖17 帶通濾波器幅頻特性Fig.17 Amplitude-frequency characteristics of bandpass filters

驗證彈道彎曲角速度重構的效果，結果如圖18、圖19所示。由式(11)可知，理論彈道彎曲角速度與速度有關，本文利用搭載試驗中獲取的速度信息計算得到的彈道彎曲角速度作為理論值。

圖18 飛行試驗頻域處理后的陀螺測量值Fig.18 Gyroscope measurement processed in frequency domain in flight test

圖19 飛行試驗彈道彎曲角速度重構效果Fig.19 Reconstruction effect of trajectory bending angular velocity in flight test

經過對陀螺儀測量的原始數據的頻域處理，可以在滿足一定精度的條件下重構彈道彎曲角速度，由于實際飛行過程中隨機噪聲較大，精度相比于數學仿真結果稍差。為避開頻域處理后陀螺儀數據端點幅值衰減現象，對31～31.8 s的滾轉角進行對準分析，每次對準均向后積分1 s。根據飛行試驗記錄，滾轉角為0°的基準信號分別在31.158 s、31.347 s、31.537 s、31.729 s時出現，記錄上述4個時刻的對準結果，圖20為滾轉角空中粗對準結果。圖21為該段時間段內滾轉角對準誤差曲線。

圖20 飛行試驗中滾轉角對準結果Fig.20 Roll Angle alignment results in flight test

圖21 飛行試驗中滾轉角對準誤差Fig.21 Roll Angle alignment error in flight test

從圖21中可以看出，對準誤差控制在2°以內，由于在飛行搭載試驗中陀螺儀測量隨機噪聲較大，不同時刻的對準精度存在一定波動。飛行搭載試驗是存在各種外界干擾及傳感器測量誤差，在此條件下仍可以保持較理想的滾轉角粗對準精度，充分驗證了本文提出的空中粗對準方法的有效性。

4 結論

本文針對制導炮彈發射后在空中難以獲取滾轉角的問題，根據矢量定姿原理，結合制導炮彈姿態運動特有的頻域特性，提出一種利用角速率陀螺敏感彈道彎曲角速度矢量的滾轉角空中粗對準方法，從而實現制導炮彈在無控段的滾轉角快速粗對準，為中制導組合導航精對準提供支撐。得出如下主要結論：

1)采用基于彈道彎曲角速度矢量的滾轉角空中粗對準方法，能夠在無控段迅速粗對準滾轉角，在角速率陀螺存在零偏、白噪聲、軸偏角的低精度條件下，粗對準精度保持在1°左右。

2)在制導炮彈復雜的飛行條件下，本文提出的滾轉角對準方法精度可達2°以內，對實際工程應用有一定的參考價值。