基于改進SOGI-FLL的旋轉彈舵機滯后測試方法
張鑫, 林凡, 沈鑫杰
(1.北京理工大學 機械與車輛學院, 北京 100081; 2.北京理工大學 宇航學院, 北京 100081)
0 引言
由于繞自身縱軸的持續滾轉,旋轉彈在簡化控制系統結構、減小制造誤差影響、避免激光攔截系統單面燒蝕等方面具有顯著優勢[1]。但是由于彈體的滾轉,旋轉彈的俯仰和偏航通道存在耦合[2],并且舵機滯后的存在會進一步產生控制耦合[3]。為消除耦合,在設計解耦方法的同時,需要對舵機的滯后進行補償[4-6]。舵機滯后產生的原因主要有兩方面:一是舵機的指令延遲,該延遲主要由于地磁等滾轉角測量傳感器存在滯后以及彈載計算機的指令滯后等原因造成;二是舵機的舵偏角響應的延遲,該延遲由舵機本身的頻率特性決定。
為補償舵機滯后,通常可使用安裝有高實時高精度滾轉角測量傳感器的單軸轉臺進行轉臺實驗,來對旋轉彈不同轉速下的舵機滯后進行標定。對于使用雙通道十字布局舵機作為執行機構的低速旋轉彈,其舵機的2個通道在彈體坐標系的舵指令均為正弦形式,以合成俯仰偏航方向的等效舵偏角[5]。因此,如果綜合考慮舵機實際輸出角度幅值的衰減,則舵機滯后測試數據處理問題最終歸結為舵機輸出舵偏角正弦曲線與標準正弦曲線之間幅值衰減和相位滯后的求取問題。
對于正弦信號幅值和相位差的處理,主要有兩種方法,即快速傅里葉變換(FFT)譜分析法和相關分析法[6-7]。FFT譜分析法本身存在相位測量時誤差較大的問題,并且該方法對噪聲敏感。相關分析法雖然原理上具有很強的噪聲和干擾抑制能力,但是由于實際測試的采樣樣本長度有限,使得測試正弦信號和噪聲信號并非完全的不相關,因此相關分析法的測試誤差與采樣點數及信號的信噪比有很大關系,另外相關分析法受信號直流分量干擾的影響嚴重。如果使用傳統的低通等濾波器對舵機滯后測試數據進行濾波以消除噪聲的影響,則會不可避免地給原正弦信號帶來因濾波造成的相位滯后和幅值衰減。
SOGI-FLL[8]方法在不同領域得到了充分運用。SOGI方法最初由Ciobotaru等[9]提出,接著Rodriguez等[10]提出使用多個SOGI加FLL的形式來檢測輸入信號不同階次諧波分量的方法。由于SOGI-FLL結構具有在電網電壓不平衡和頻率突變工況下良好的鎖頻特性,廣泛應用于電網并網時電壓基波信號的提取中[11]。SOGI結構簡單,能夠將輸入的正弦信號v在共振頻率下無滯后無衰減地濾波[12],當使用FLL自動調節共振頻率到v的基波頻率時,便能夠得到與v基波同幅值同相的純凈的信號v′和與其正交的信號qv′,再經過帶有PI環節的鎖相環(PLL)處理,便可以得到輸入正弦信號v的幅值和相位[13]。
目前,學者們對基于SOGI的FLL/PLL技術在電網系統中的應用進行了大量研究,特別是通過線性近似后的解析分析,給出了SOGI-FLL/PLL的參數調節指導方法,以獲得需求性能[14-16]。針對輸入信號中各階次諧波的進一步抑制以及直流分量偏移影響的消除問題,學者們對SOGI-FLL/PLL進行了不斷改進[17-18]。近年來,SOGI-FLL/PLL技術也被應用于永磁同步電機無傳感器控制中,用以從反電動勢波形中觀測電機轉子的角位置[19]。
本文使用改進SOGI-FLL方法對舵機滯后測試數據進行處理,實現在測試數據基波頻率處的無滯后無衰減的濾波,解決了傳統的FFT譜分析法和相關分析法噪聲敏感的問題。由于舵機存在標定誤差,舵偏角反饋中存在常值偏移,這也是滯后角測試中需要解決的問題。本文首先建立了旋轉彈舵機滯后模型,接著在常規SOGI-FLL的基礎上加入常值偏移補償回路進行改進,并對改進SOGI-FLL的傳遞函數進行了詳細分析。然后對帶有PI環節的PLL相角估計方法的原理進行了建模,并給出了PI參數選取方法。最后使用仿真及實驗數據對改進SOGI-FLL方法的有效性進行了分析,并將處理結果與FFT譜分析法及相關分析法的處理結果進行了對比。
1 旋轉彈滯后分析
旋轉彈舵偏角關系示意圖如圖1所示。圖1中,Ox1y1z1和Ox4y4z4分別為彈體坐標系和準彈體坐標系[20],γ為滾轉角,δz4和δy4分別為準彈體坐標系Ox4y4z4中俯仰舵和偏航舵的等效舵偏角;舵面十字布局,其中舵面1和舵面3聯動,由一路舵機控制,構成俯仰舵,δz1為彈體坐標系Ox1y1z1中的實際舵偏角;舵面2和舵面4聯動,由另一路舵機控制,構成偏航舵,δy1為彈體坐標系Ox1y1z1中的實際舵偏角。

圖1 舵偏角關系Fig.1 Actuator angles
可得彈體坐標系和準彈體坐標系下的舵偏角關系為
(1)
在旋轉彈控制中,飛控系統產生的是準彈體坐標系的等效舵偏角指令,根據彈上滾轉角傳感器測量輸出的滾轉角γ(t),飛控將該等效舵偏角指令轉化為彈體坐標系的實際舵偏角指令給兩路舵機,舵機響應指令做出動作。

(2)
進一步可寫成如下正弦信號形式:
(3)


(4)
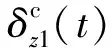
2 改進SOGI-FLL滯后角處理模型
2.1 改進SOGI-FLL模型推導
通過改進的SOGI-FLL方法對轉臺實驗得到的測試數據進行處理。改進的SOGI-FLL結構如圖2所示。圖2中,為輸入的帶有噪聲及常值偏移的正弦信號,′和q′為根據輸入觀測得到的兩正交信號,為經過補償的輸入信號,εe和εf分別為同步誤差信號和頻率誤差信號,e為估計角頻率,kdc和kSO以及Γ均為增益,x為定義的狀態量,s為拉普拉斯算子。

圖2 改進SOGI-FLL結構Fig.2 Structure of the improved SOGI-FLL
首先不考慮改進部分,只對圖2中標出的傳統SOGI-FLL部分進行分析。按照文獻[20]中的推導,可以得到如下傳遞函數:
(5)
式中:D(s)為帶通濾波器,并且在頻率e處無衰減無滯后;Q(s)為低通濾波器,在頻率e處無衰減,二者相位始終相差90°,因此生成的′和q′兩信號正交。同時文獻[20]給出了結論,FLL的估計角頻率e會收斂于輸入信號的角頻率,收斂的速度與增益Γ的取值有關。由于Q(s)為低通濾波器,當測試數據中含有低頻干擾乃至常值偏移時,q′將受到影響。因此如圖2所示,加入常值偏移補償回路進行改進,有
(6)
式中:zdc(s)為常值偏移補償項傳函。整理得到由到zdc的傳遞函數Z(s)
(7)
由圖2可知有
[(s)-zdc(s)]D(s)=′(s)
(8)
(9)
由
(10)
(11)
將式(5)代入式(9)和式(11),得到
(12)
由勞斯判據可知當kdc和kSO均大于0時,式(12)對應的系統穩定。觀察Dm(s)和Qm(s)的形式,可得二者相位始終相差90°,′和q′兩信號保持正交。為對比改進效果,取kdc=1,kSO=0.7和e=5 Hz后,畫出D(s)、Q(s)、Dm(s)和Qm(s)的Bode圖如圖3所示。

圖3 傳遞函數D(s)、Q(s)、Dm(s)和Qm(s) Bode圖Fig.3 Bode plot of the transfer functions D(s), Q(s), Dm(s) and Qm(s)
由圖3可見:D(s)和Dm(s)在e附近及高頻段的幅相頻特性相似,為帶通濾波器,均在e頻率處無衰減無滯后,但是在低頻段Dm(s)濾波效果更好;Q(s)和Qm(s)在e附近及高頻段的幅相頻特性相似,在e頻率處幅值無衰減,相位滯后90°,但是在低頻段,改進后得到的Qm(s)不再是低通濾波器,而是可以有效濾除常值偏移分量,這也是對SOGI-FLL進行改進的主要目的。
文獻[15-17]對調節kSO產生的效果進行了詳細分析,減小kSO能增強濾波作用,但是增大系統調節時間;反之增大kSO會減弱濾波作用,但使系統調節時間變快。下面考慮kdc的影響,對式(12)中的傳遞函數Dm(s)和Qm(s)進行分析可知,kdc主要在低頻段起作用,增大kdc會使低頻段濾波作用增強。取kSO=0.7和e=5 Hz,當kdc分別取值為0.4、1.0和1.6時,Dm(s)和Qm(s)的Bode圖如圖4所示,可見增大kdc后Dm(s)和Qm(s)的幅頻特性曲線在低頻段會加速衰減。

圖4 傳遞函數Dm(s)和Qm(s)不同kdc值下Bode圖Fig.4 Bode plot of the transfer functions Dm(s) and Qm(s) with different values of kdc
2.2 PLL相角和幅值估計
由2.1節已知′和q′為兩正交的正弦信號,因此可設兩信號分別為
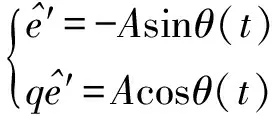
(13)
式中:A為幅值;θ(t)為相角。圖5為PLL結構,其中kp、ki分別為比例系數和積分系數。

圖5 PLL結構Fig.5 PLL structure

(14)

(15)
由圖5有如下拉氏變換:
(16)
由式(16)可得PLL傳遞函數為
(17)
由式(17),通過合理選取kp和ki,使相角估計(t)快速收斂到θ(t)。可采用2階傳遞函數的極點配置方法,通過選取阻尼比ξ和自然頻率ωn,利用
(18)
得到kp和ki的選取方法
(19)
(20)
綜上所述,在得到改進SOGI-FLL輸出的正交信號后,可對輸入信號的相角和幅值進行估計。


圖6 滯后角和幅值估計Fig.6 Estimation of lag angle and amplitude
3 仿真驗證與實驗分析
3.1 仿真驗證
為驗證本文提出的SOGI-FLL在旋轉彈舵機控制滯后測試數據處理中的有效性,分別使用仿真數據和轉臺實驗測試數據進行驗證。首先使用MATLAB/Simulink平臺進行仿真驗證。


圖7 仿真用和信號


圖8 ′和q′仿真結果Fig.8 ′ and q′ simulation results

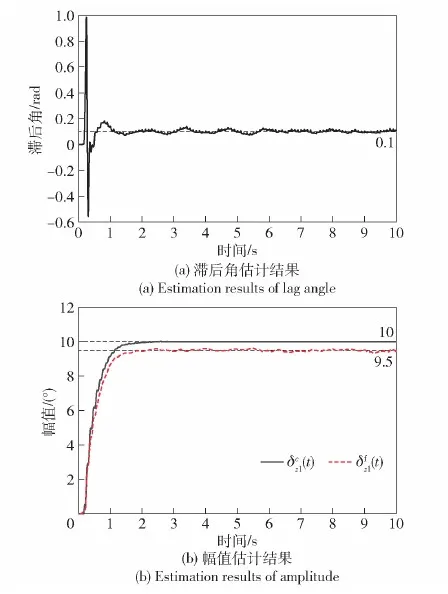
圖9 滯后角及幅值估計結果Fig.9 Estimation results of lag angle and amplitude
由于相關分析法在信號有常值偏移時存在原理性誤差,相關分析法在此種仿真情況下不適用,在此不使用相關分析法進行處理。

圖10 仿真FFT結果Fig.10 FFT simulation results
由表1可見,對于本次仿真,使用改進SOGI-FLL方法處理得到的結果相比于FFT方法,幅值衰減因子測試相對精度提高約0.21%,相位滯后測試相對精度提高約0.80%。由于旋轉彈舵機滯后角測試結果直接影響旋轉彈舵機滯后補償,進一步直接影響旋轉彈俯仰和偏航通道的耦合。因此認為當采用改進SOGI-FLL方法的測試結果進行解耦補償可提高1%量級的精度時,以文獻[3]提出的典型最優舵面超前角度補償方法的控制耦合在20%以下為參考,可知改進SOGI-FLL方法能較大程度地提高旋轉彈解耦精度。

表1 仿真結果Table 1 Simulation results
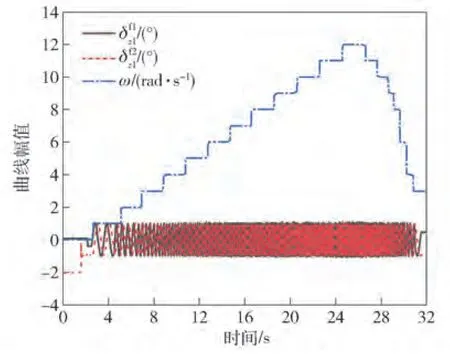
圖11 實驗曲線Fig.11 Experimental curves
3.2 實驗分析


圖12 轉速恒定段實驗曲線Fig.12 Experimental curves of the section with constant speed

圖13 轉臺實驗幅值和滯后角Fig.13 Amplitude and lag angle results in turntable experiment


表2 實驗結果Table 2 Experimental results

圖14 實驗FFT結果Fig.14 FFT experimental results
綜上,通過仿真和實驗數據,驗證了改進SOGI-FLL方法在旋轉彈舵機控制滯后測試數據處理中的有效性,并且相對于FFT方法和相關性分析方法,改進SOGI-FLL在存在噪聲和常值偏移下的處理精度更高。
4 結論
本文針對旋轉彈舵機滯后測試中存在的噪聲及常值偏移問題,利用改進SOGI-FLL對測試數據進行處理,提高了滯后角測試精度。得出主要結論如下:
1)建立了旋轉彈準彈體坐標系和彈體坐標系舵偏角之間關系,得到轉臺實驗中旋轉彈舵機幅值衰減因子和滯后角的模型,得出滯后角測試問題等效為從帶有噪聲及常值偏移的正弦信號中提取相位和幅值問題的結論。
2)在常規SOGI-FLL中加入了常值偏移補償回路進行改進,改進SOGI-FLL具有常值偏移濾除能力,并且在正弦信號基波頻率處無滯后無衰減的濾波,可有效消除測試數據中的噪聲和常值偏移的影響,并使用帶有PI環節的PLL進行相角估計,可有效提高測試精度。
3)通過仿真和實驗數據驗證,改進SOGI-FLL在測試數據受噪聲和常值偏移影響時,相比FFT方法和相關分析法,數據處理精度得到了有效提高。

