基于增強上下文信息長短期記憶網絡的彈道軌跡預測

任濟寰， 吳祥， 薄煜明， 吳盤龍， 何山

(南京理工大學 自動化學院, 江蘇 南京 210094)

0 引言

根據己方的觀測數據進行彈道軌跡預測，是提升現代陸軍反應速度和打擊精度的重要手段。在陸軍的進攻及防御反制措施中，對來襲彈進行攔截時，要求對彈道軌跡進行精準且高效的預測。

現役火控系統對彈道預測主要采用解算時間較短的射表函數逼近方法，通過建立運動學或動力學模型，利用函數逼近法等進行軌跡預報[1]。該方法設計過程繁瑣、精度有限，且不同彈種的具體彈道和修正量需要分別解算，不利于火控系統的通用性發展[2]。為克服上述問題，基于數值積分法求解彈道微分方程組的方法被逐漸應用起來。該方法利用雷達獲得來襲彈現在點位置、速度矢量及彈道參數，通過彈道解算來確定炮彈的未來運動軌跡[3]。彈道方程預測法雖然通用性較好，但需要多次彈道迭代才能得到較高精度的結果，實時性不強。

除以上彈道軌跡預測方法外，考慮到彈道軌跡是時序數據，可采用時序預測的方法對雷達采樣數據進行處理、分析并進行預測。近年來，在機器學習領域涌現了一批優秀的時序預測方法，其中包括經典結合隨機過程的高斯過程回歸(GPR)[4-6]及高斯混合模型(GMM)[7]。考慮到彈道軌跡是一段復雜的非線性曲線，可將炮彈的軌跡視為一個隨機過程，而隨機過程可以表達為基于某一核函數的高斯過程(GP)。GP作為一個特殊的隨機過程，它結合了貝葉斯后驗概率和核方法，提供了一個有效的概率方法用于回歸問題。當GP用于處理回歸問題時，被稱為GPR，而GMM使用不同類型的核函數分別做GPR建模，最后對各自輸出結果進行加權線性組合，進一步提高了預測精度。GMM預測法中，核函數直接決定了GPR的預測精度，它用于捕捉不同輸入點之間的關系，從輸入的訓練數據預測未知點的值。文獻[8]使用GMM，通過所收集的傳感器數據和操作監控信息對復雜工業系統組件的剩余壽命進行預測。文獻[9]利用GMM預測新冠疫情在全球的預期病例、死亡總數、結束日期。GMM具有容易實現、超參數自適應獲取的優點，但其存在因為非參數性質導致計算量大的問題，在面對大數據集時存在應用瓶頸[10]。

近年來，受人腦工作原理啟發而設計的神經網絡迅猛發展，其旨在模擬人腦的學習過程，實現對信息的智能處理及進一步決策。時序預測是神經網絡研究的一個重要領域，在處理時序信息的過程中，記憶是學習的核心環節。卷積神經網絡(CNN)[11]主要具有空間記憶能力。文獻[12]使用CNN對飛機的三維飛行軌跡進行預測，但受限于CNN有限的時序記憶能力，只能將飛行軌跡拆為3個坐標軸上的分量分別預測，其應用前景有限。

為更好地形成時空記憶，循環神經網絡(RNN)[13]通過隱狀態傳遞時序信息。RNN中每個隱狀態都會在下一時刻被更新，對短期內的信息更為敏感。在一些復雜場景，如軍用、戰場等環境中，往往需要處理較大規模的時序數據，要求神經網絡必須具備長期記憶能力，RNN就顯得力不從心。同時，RNN還存在難以訓練、收斂速度緩慢，并時常伴有致命的梯度消失與梯度爆炸等問題。長短期記憶(LSTM)網絡[14-16]克服了傳統RNN網絡存在的大部分問題，能夠從時空特征中提取出有效的信息。文獻[17]提出使用LSTM網絡對戰場目標進行建模，通過對其軌跡的預測來感知和預測戰場態勢，體現出了LSTM網絡在時序數據處理領域的優勢。但目前將LSTM網絡用于炮彈軌跡預測在國內外公開發表的文獻中未見報道。

針對彈道軌跡預測問題，本文提出了上下文增強的長短期記憶(CE-LSTM)網絡，進一步加強短期時序特征之間的關聯性，以模擬炮彈在飛行過程中的運動狀態。用實際彈丸參數建立包含13 500條不同口徑及氣象條件的彈道軌跡樣本數據集，以保證仿真結果的真實性。利用數據集中樣本的最后20 s軌跡的空間坐標，對CE-LSTM網絡進行訓練、驗證及測試。通過對比外彈道數值解法及GMM等方法，表明CE-LSTM網絡在有效保證實時性的同時提高了預測精度。

1 CE-LSTM網絡軌跡預測模型

1.1 LSTM網絡簡介

LSTM網絡是一種應用在深度學習特殊領域中的循環神經網絡，它克服了RNN訓練過程中的梯度爆炸和梯度消失問題，并針對短期記憶的問題進行了優化，能夠建立較長距離的時間依賴關系，在1997年由Sepp等首次提出[18]。LSTM網絡的核心在于引入了用于循環傳遞信息的LSTM單元(LSTM Cell)，能夠建立有效的時序依賴關系，適用于軍用場景中復雜時序數據的處理。同時，它也通過LSTM單元緩解了RNN訓練過程中存在的梯度爆炸和梯度消失等問題。

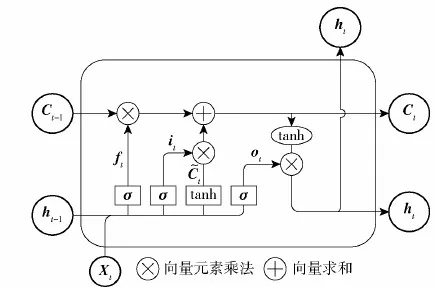
圖1 LSTM單元Fig.1 LSTM unit

LSTM單元中門控單元的工作機制和流程依次為：遺忘門以Xt和ht-1為輸入，經sigmoid函數壓縮至(0,1)區間后與Ct-1數乘，其中1表示全部保留，0表示全部丟棄，從而決定將要從Ct-1中丟棄哪些信息，其表達式如下：

ft=σ(Wf[ht-1,Xt]+bf)

(1)

式中：Wf、bf分別為遺忘門的權值與線性偏置。

并非所有的新信息都會被存入Ct，輸入門的輸入與遺忘門相同，其作用是過濾。輸入門決定了哪些新信息可以存入Ct，其表達式如下：

it=σ(Wi[ht-1,Xt]+bi)

(2)

(3)

式中：Wi、bi分別為輸入門的權值與線性偏置；Wc、bc分別為LSTM單元的權值與線性偏置。

(4)

最后由輸出門對網絡單元最終的輸出進行控制，其表達式如下：

ot=σ(Wo[ht-1,Xt]+bo)

(5)

ht=ot·tanh(Ct)

(6)

式中：Wo、bo分別為輸出門的權值與線性偏置。該單元的輸出ht分為隱藏層向更深層網絡的輸出以及橫向上對該層中其他神經元的輸出。

1.2 CE-LSTM模型

考慮到陸軍常規火炮的彈藥在發射后不具備主動改變軌跡的能力，氣象等條件在局部范圍內對其軌跡影響有限，因此彈道軌跡本質上是一條連續的、短時段內有一定規律的復雜且光滑曲線，具有時序關聯性強的特點。與尋常時序數據不同，彈道軌跡中當前時刻炮彈位置與上一時刻數據的聯系非常密切，在使用LSTM網絡對炮彈軌跡進行預測時對其進行相應的改進，在不丟失長期記憶的前提下進一步加強短期記憶，以獲得更佳的性能表現。

圖2 CE-LSTM單元Fig.2 CE-LSTM unit

由式(6)可見，循環結構單元在當前時刻隱藏層的輸出ht僅取決于當前時刻的ot與Ct，沒有著重考慮炮彈當前時刻位置信息對下一時刻的影響。針對該問題，CE-LSTM在原有LSTM循環結構單元的基礎上，充分考慮計算效率以及相鄰幀短時上下文信息利用效率，構建隱藏層輸出混合單元，對當前時刻隱藏層上輸出ht的形式進行改進。具體地，引入一個超參數α作為隱藏層輸出的權值，將當前時刻隱藏層輸出與前一時刻LSTM單元的隱藏層輸出進行線性加權組合，作為當前時刻的最終隱藏層輸出。CE-LSTM循環結構單元的結構如圖2所示，其中h′t為隱藏層輸出混合單元的輸出，α取值為0.9，

h′t=α·ht-1+(1-α)·ht

(7)

通過構建隱藏層輸出混合單元，任意兩個連續時刻之間產生了更緊密的聯系。在不損失長期記憶信息的情況下，大大增強了短期記憶能力以及短期記憶之間的相關性，使網絡結構更適用于炮彈軌跡預測場景。

2 基于CE-LSTM的軌跡預測

彈道軌跡預測是利用火控雷達所獲得的一定幀數炮彈在三維空間中連續的坐標，對該彈體之后的彈道軌跡進行預測。

2.1 彈道軌跡預處理

在彈道軌跡預測問題中，每一條樣本軌跡都存在多個潛在特征，這些特征往往存在量綱和數值量級上的差異，若使用原始樣本軌跡數據而不加處理，則會使神經網絡難以訓練，無法收斂。標準化可以克服以上問題，它為不同潛在特征提供統一的尺度，使不同的特征具有可比性。在神經網絡利用梯度進行訓練和學習參數時，標準化后的數據可使不同特征對同一參數的影響程度一致，從而加快訓練時梯度下降的速度，提高模型在迭代過程中的收斂速度，故應該對數據集做標準化處理。在不改變樣本數據原有概率分布的情況下，標準化使每條軌跡樣本數據均值為0、標準差為1，其公式如下：

(8)

式中：x′為經過標準化后的樣本；x為原始樣本；μ為全體樣本的均值；ρ為全體樣本的標準差。

2.2 彈道軌跡預測流程

外彈道學的研究表明，影響彈道的因素眾多，除溫度、濕度、氣壓等較穩定的基本氣象條件之外，還有橫風、縱風等不確定性強、波動幅度較大的干擾因素。因此對彈道軌跡的預測需要一個強時空相關性且高度復雜的非線性模型。LSTM理論上具有可以擬合任意非線性函數的優秀特質，而CE-LSTM在此基礎上進一步加強了模型對相鄰幀相關性特征的提取。

本文利用CE-LSTM進行彈道軌跡預測，其過程遵循以下步驟：

步驟1處理各型火炮的彈道數據，取彈丸命中目標前20 s的末段數據。

步驟2標準化數據。

步驟3由標準化后的彈道數據建立彈道軌跡的時序數據集，包括訓練集、驗證集和測試集。

步驟4構建CE-LSTM模型，設置參數和超參數后利用訓練集訓練CE-LSTM預測模型，并使用驗證集驗證模型的表現，直到模型達標。

步驟5將測試集中每個樣本一定幀數的炮彈在三維坐標信息輸入CE-LSTM模型，由模型進行預測并輸出炮彈后續20 s的軌跡。

詳細的彈道軌跡預測模型的訓練及預測流程如圖3所示。

圖3 模型訓練及預測流程Fig.3 Model training & prediction flowchart

3 仿真實驗與分析

3.1 實驗設定

3.1.1 構建訓練集與測試集

為讓模型得到有效訓練，本文通過采樣不同氣象條件、不同彈道條件、不同射擊諸元等不同條件下的各種彈道軌跡，構建軌跡樣本共13 500條，其中包含155 mm榴彈炮、122 mm榴彈炮、35 mm高射炮等3種不同口徑的陸軍常規火炮各4 500條樣本，它們分別以700 m/s、690 m/s、1 050 m/s的初速發射彈丸，武器高低角除35 mm高炮為30°～80°外，其他均為25°～65°。選擇使用多種不同類型彈道訓練同一個預測模型的目的，是因為在實戰中同時來襲的炮彈種類可能較多，若針對每一種彈道單獨訓練一個預測模型，則雖然精度會更高，但是會因為辨識彈道產生額外的計算開銷而影響實時性。此外，彈道辨識的準確性難以保證，存在錯誤辨識彈道類型并使用錯誤模型預測的“誤判”風險，大大犧牲預測模型的魯棒性。

為使預測模型更貼近實戰情況，在構建數據集時為3種火炮的彈頭初速均加上-30～30 m/s的隨機誤差，以模擬火炮發射過程中強烈沖擊與震蕩對彈頭初速造成的波動；為武器高低角加上-1°～1°的隨機誤差，以模擬跳角的誤差。為武器高低角加上隨機誤差的意義除模擬誤差外，還在于模擬敵方多次開火時重新瞄準所造成的武器線變動。隨機誤差的加入不僅貼近實戰，還讓預測模型具備了更強的魯棒性和泛化能力，使模型在面對未知軌跡時也能做出準確預測。

火炮發射過程中除武器線的變化之外，風速是影響外彈道的另一個極不穩定且重要的因素，其中橫風和縱風影響最大。為此，在同一口徑火炮的4 500條軌跡中，包含以下3種風況各1 500條：隨機選取8～12 m/s的恒定風力；每0.1 s隨機選取8～12 m/s的時變風力；每0.1 s增加0.02 m/s的線性時變風力。不同風況的引入進一步增強了外彈道的不確定性和非線性，雖然會增加模型訓練難度但同樣有利于增強模型的魯棒性和泛化能力。數據集構成如表1所示。

表1 數據集構成Table 1 Composition of datasets

將3種口徑火炮每種風況的1 500條軌跡中取出1 450條軌跡作為訓練集，40條軌跡作為測試集，剩余10條作為驗證集。

3.1.2 CE-LSTM網絡結構

網絡結構是影響神經網絡預測準確率的另一個決定性因素，在固定超參數的條件下，不同網絡結構的性能表現天差地別，為獲得高預測準確率，選擇合適的網絡結構非常重要。本文采用的CE-LSTM網絡結構包括輸入層、隱藏層、回歸層三部分，其中輸入層和回歸層形式固定，故確定網絡結構主要是對隱藏層進行設計。CE-LSTM炮彈軌跡預測網絡結構如圖4所示。

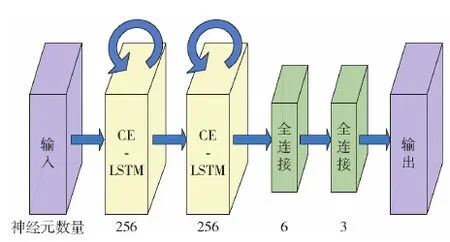
圖4 CE-LSTM網絡結構Fig.4 Schematic diagram of the CE-LSTM network

網絡在獲得輸入后共使用4層隱藏層：包括2層CE-LSTM和2層全連接層。其中2層CE-LSTM層再搭配適當的激活函數即可表示足夠精度的決策邊界，并可以擬合足夠精度的平滑映射。隱藏層內部的設計主要是選擇數量合適的神經元。在神經元數量選擇時，一方面，全連接層分別選擇6個和3個神經元，是為了數據傳遞時呈倒三角型逐層壓縮，最后形成3維輸出。另一方面，在其他參數、超參數和結構固定的條件下，為每層CE-LSTM分別選擇16、32、64、128、256、384、512個神經元，并在訓練神經網絡時，每50次迭代采樣一次當前網絡模型在驗證集上的均方根誤差(RMSE)，以確定最優神經元數量。不同數量神經元設定下預測的均方根誤差如圖5所示。

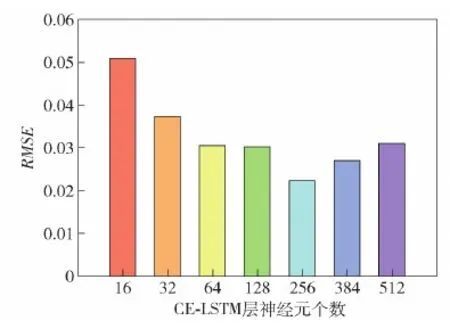
圖5 不同數量神經元對應RMSEFig.5 RMSE with different number of neurons

由圖5可知，神經網絡在測試集上由RMSE度量的預測準確率隨神經元數量的增加呈先減小后增大的趨勢，且在256個神經元時RMSE最小。此外，神經元數量應盡量選擇2的整數次冪，最大限度利用GPU的并行計算資源，提高計算速度，故每層CE-LSTM使用256個神經元。此外，包括隱藏層層數在內的其他參數調節均采用同樣方法，通過重復探索來進行局部優化，以獲得一組使模型預測精度令人滿意的參數組合。

對輸入權重及循環權重引入L2正則化以降低過擬合風險，訓練CE-LSTM網絡時初始學習率經過多次試驗后選擇0.001，且每訓練10輪便將學習率減半，既能保證收斂速度，又可在多輪迭代后使學習率盡量小，以逼近損失函數的全局最優值。

3.1.3 對比方法

3.1.3.1 彈道方程預測法

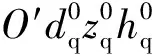
(9)

式中：vd、vz、vh分別為炮彈速度矢量在三坐標軸上的分量；C為彈道系數；Hτ(hq)為虛擬氣壓函數；G(vrτ)為虛擬阻力函數；wd、wz、wh分別為縱風、橫風、垂直風的風速；az(t)為偏流加速度。

彈道方程預測法的實施分為三步，首先根據雷達探測到的炮彈軌跡，濾波估計出其坐標位置與速度矢量；其次將濾波估計的結果作為輸入量代入彈道方程，得到關于彈道系數的方程，解方程得到彈道系數；最后將濾波估計的最新結果作為彈道起始條件，利用上一步得到的彈道系數，代入彈道方程組，使用4階龍格- 庫塔法[20]解算炮彈的未來軌跡。

3.1.3.2 GMM預測法

在確定核函數時，為符合炮彈軌跡的特點，本文選擇平方指數函數(SE)與有理二次函數(RQ)作為核函數，分別用kSE(r)、kRQ(r)表示，它們對應的GP均有光滑、平穩且無限可微的優秀性質，其一般表達式如下：

(10)

(11)

式中：β、l>0為待確定的超參數，l表征特征長度尺度；r為任意兩個隨機變量之間的距離。

GMM預測過程為：首先，將炮彈軌跡拆分為3個坐標軸上的獨立運動軌跡，并分別用GP表示；其次，將3條軌跡代入GPR回歸模型進行預測；最后，將預測結果重新整合為3D空間上炮彈的預測軌跡。t時刻單一坐標軸上的預測數據點Xt可表示為

Xt=ξxt,SE+ηxt,RQ

(12)

Pt={Dt,Zt,Ht}

(13)

3.2 實驗結果與分析

3.2.1 訓練結果評估

使用訓練集中的12 900條軌跡數據，訓練CE-LSTM網絡模型，記錄訓練過程中訓練集的損失變化情況，如圖6所示。

圖6 不同數量神經元對應損失Fig.6 Loss with different number of neurons

設定訓練400輪作為停止優化損失函數的停止條件。將擬合誤差邊界定義為：驗證集損失小于0.000 05，且最后10輪訓練時，驗證集損失的均值與訓練集損失的均值之比小于1.15。通過400輪訓練中損失函數值的變換情況可知，CE-LSTM網絡損失下降非常迅速，可在短短幾輪后降到0.1%左右，并在第50輪左右趨于零，在此之后雖然驗證集的損失會有所波動，但始終與訓練集的損失接近。在第150輪左右將圖6藍色矩形框中曲線放大，可見損失降至十萬分位水平，測試集損失曲線平穩，小于上述擬合誤差邊界，因此認為網絡已收斂。

3.2.2 彈道預測結果分析

使用訓練好的CE-LSTM網絡對測試集中的軌跡進行預測，隨機挑選具有代表性的4條軌跡，展示預測結果。在給定前1 s共100個坐標值和前0.5 s共50個坐標值的情況下，CE-LSTM和對比方法的預測結果分別如圖7和圖8所示。為進一步分析各種模型在預測軌跡時的特點，選擇圖8(a)中155 mm榴彈炮彈丸在全程恒定8～12 m/s隨機風力情況下的軌跡，分別作出3種預測模型在3個方向上預測值的絕對誤差隨時間變化的曲線，如圖9所示。

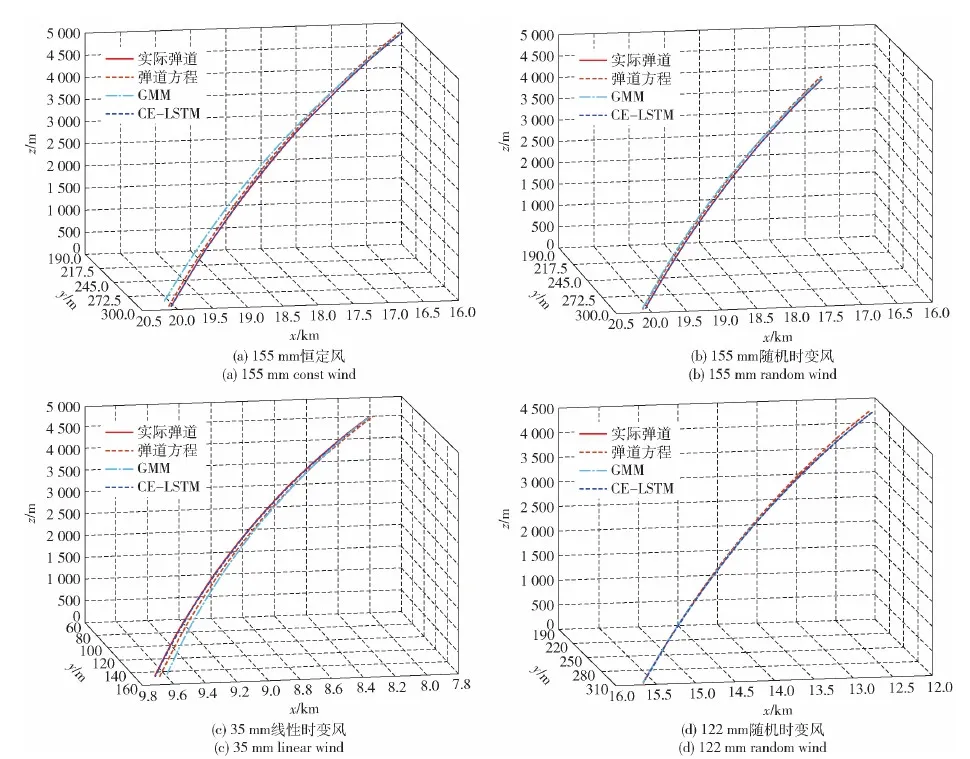
圖7 基于前100個坐標值的預測結果Fig.7 Prediction results based on the first 100 coordinate values

圖8 基于前50個坐標值的預測結果Fig.8 Prediction results based on the first 50 coordinate values

結合圖7與圖8的8組預測表現來看，CE-LSTM網絡的預測結果精度最高，整體表現平穩，該網絡在預測軌跡時幾乎不受外界不確定因素影響，可以對各型火炮在不同氣象條件下的炮彈軌跡進行精確預測。GMM模型的表現在軌跡初始段良好，但其精度隨時間推移整體呈逐漸下降的趨勢，誤差不斷累積，導致在軌跡末端的表現不佳。彈道方程解算模型的表現雖然整體較為平穩，但精度較低，同樣存在誤差隨時間積累的問題，并在軌跡初始段表現也不如其他兩種模型。

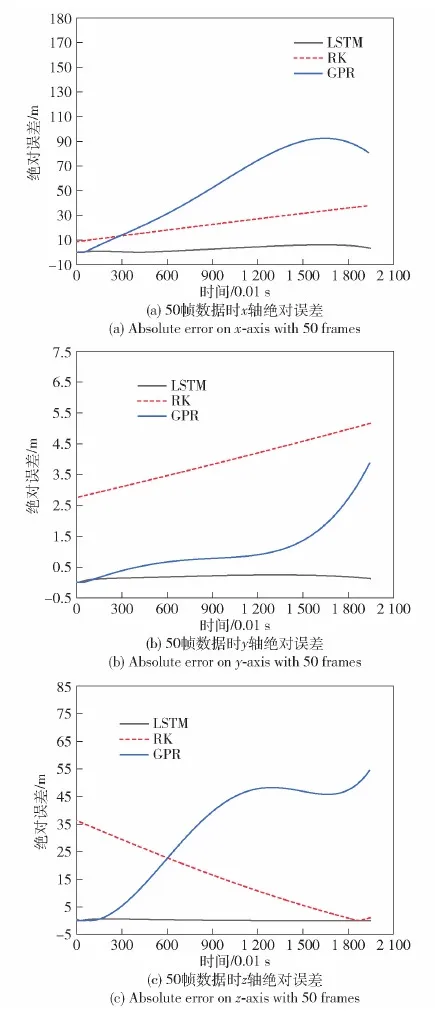
圖9 不同坐標軸上的絕對誤差Fig.9 Absolute errors for different coordinate axises

由圖7(c)與圖8(c)可知，無論是GMM方法還是彈道方程解算法，預測精度均明顯低于其他組，其原因是35 mm高炮彈丸自重僅0.685 kg，遠低于155 mm榴彈炮彈丸52.8 kg及122 mm榴彈炮彈丸21.76 kg，因此外彈道受氣象條件，諸如橫風與縱風的擾動所造成的影響被放大，導致其彈道非線性程度增大，軌跡復雜、更難預測，而CE-LSTM網絡表現依然良好，可見該模型在高擾動下的魯棒性優于其他兩種，得益于神經網絡能夠擬合任意非線性曲線的良好性質。

以圖7(a)與圖8(a)為例，橫向對比各模型在相同氣象條件下，在給定不同時長坐標值時的表現，并以預測值的均方根誤差度量，結果如表2所示。

由表2可知，提供給模型的觀測值數量越多，其預測精度越高，這一趨勢在彈道方程解算模型中表現尤為突出。

圖9形象地刻畫了各種模型的特點，可見CE-LSTM網絡的表現在全時段良好且平穩；GMM模型受累積誤差影響嚴重，逐漸發散；彈道方程模型精度低，且呈接近線性的趨勢發散，注意到圖9(c)雖然誤差看似逐漸降低，但其末段有重新上升趨勢，可以預估其隨時間推移，依然會發散。

綜上，可認為CE-LSTM網絡能夠在全時段精確地進行炮彈軌跡預測，GMM模型的預測結果在初始的2～3 s內可用，其在3個方向上的平均RMSE略大是因為軌跡中末段發散導致，而彈道方程解算模型所預測結果的可用區間則更窄。

表2 不同時長坐標值下均方根誤差表Table 2 RMSE with different time-length coordinate values

3.2.3 模型泛化能力測試

為進一步測試本文所提方法的魯棒性并驗證其泛化能力，在去掉原數據集中橫風、縱風等氣象條件的影響，保持原有射擊諸元、彈道條件不變的情況下，重新構建一個不含橫風與縱風影響的數據集，按照2.2節方法，訓練一個CE-LSTM預測模型，簡稱無風模型。之后，使用無風模型預測有橫風、縱風影響的軌跡數據，隨機選取兩條預測軌跡如圖10所示。

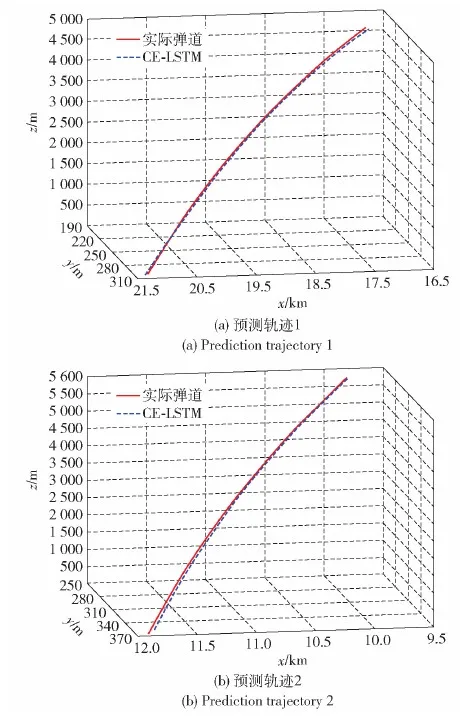
圖10 泛化能力交叉驗證Fig.10 Cross-validation for generalization capability

由圖10可知，CE-LSTM預測模型的表現在有一定相關性的全新數據集上雖然有所下降，但整體預測精度依然較高。通過這種交叉驗證的方式，證明了本文所提方法的魯棒性和泛化性較強，可以對一些未經訓練的彈道軌跡進行較為準確的預測。

3.2.4 預測用時分析

本文通過對測試集中所有彈道軌跡進行預測，并求取各種模型預測用時的平均值方式，有效地說明CE-LSTM網絡在實時性上的優勢。在MATLAB2020環境下(Windows 10，R7-4800H CPU，2.9 GHz 主頻，Nvidia RTX2060-MaxQ GPU，16GB RAM)其結果如圖11所示。由圖11可以看出，本文所提方法在預測階段的平均用時遠低于GMM方法與彈道方程方法：比GMM快約3倍，比彈道方程方法快約10倍。

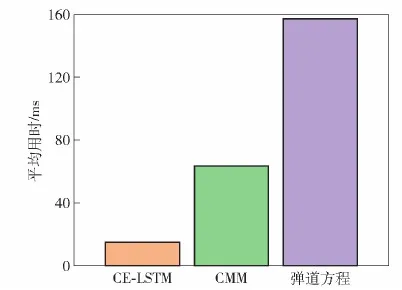
圖11 預測平均用時Fig.11 Average prediction duration

4 結論

本文在LSTM網絡的基礎上提出了基于新型CE-LSTM網絡的彈道軌跡預測方法，構建隱藏層輸出混合單元，更適合彈道軌跡預測場景。通過仿真實驗證明了該方法相比GMM方法和彈道方程解算方法，在預測精度和實時性上均有大幅提升，而且泛化能力測試證明了本文所提方法有能力預測一些有相關性的全新彈道軌跡。

目前本文方法暫停留在仿真階段，在工程實際中面臨的難點是如何獲取足量的敵方數據以訓練預測模型，可行的方案是先用仿真數據和我方數據對模型進行預訓練，再用有限的真實彈道數據進行微調，通過在線學習的方式提高模型的實戰精度。

在后續工作中，將實彈軌跡數據加入訓練集，并在靶場驗證模型的實戰精度。此外，彈道軌跡預測是順著來襲彈的軌跡進行的，后續工作可以考慮利用CE-LSTM模型逆軌跡而行，對來襲彈軌跡進行反向推演和坐標轉換，從而準確得出敵方火炮位置，進行反制和相關反火炮應用的研究。