基于圖特征學習的海雜波抑制算法
陳鵬, 許震, 曹振新, 王宗新
(東南大學 信息科學與工程學院 毫米波國家重點實驗室, 江蘇 南京 210096)
收稿日期:2021-10-09
基金項目:江蘇省優秀青年科學基金項目(BK20220128);國家重點研發計劃項目(2019YFE0120700);中國航天科技集團公司第八研究院產學研合作基金資助項目(SAST2021-039);國家自然科學基金項目(61801112)
0 引言
在海洋探測雷達系統中,雷達照射海面所產生的后向散射回波稱為海雜波[1]。由于海洋雷達受到復雜海況所產生的海雜波影響,極大地降低了雷達監視和檢測目標的能力[2]。因此,從海洋雷達接收的信號中抑制海雜波分量是亟需解決的問題。
由于海面的復雜運動,導致海雜波具有非線性、非高斯、非平穩特征[3]。傳統的隨機信號處理方法一般建立在信號是平穩性的假設前提下,單純采用時域或頻域的單一特征無法有效地描述海雜波的復雜特征。通過引入時頻變換的理論構造基于時域和頻域的聯合二維處理方法,將一維的時間信號投射成時間- 頻率的二維圖像,可以得到描述時間- 頻率- 能量三者關系的時頻譜,更加直觀地觀測到信號在時頻域上的局部變化規律[4]。目前,針對海雜波時頻變換的主要方法有短時傅里葉變換(STFT)、魏格納- 維爾分布(WVD)和小波變換(WT)等[5]。其中,STFT計算簡便,但時頻分辨率無法同時達到最優;WVD時頻分辨率可以同時達到理想情況,但在分析多分量信號時會產生嚴重的交叉項干擾;WT的多尺度分辨特性適合于分析非線性、非平穩信號,但受到小波基函數的約束,導致適應性較弱。
隨著近年來機器學習領域的迅速發展,人工智能算法也廣泛運用于海雜波的處理領域中。針對海雜波的仿真建模,可以通過反向傳播神經網絡和門控循環神經網絡進行幅度預測和參數估計[6-7]。在海面的弱小目標檢測中,深度學習和遷移學習被廣泛運用[8-10]。在海雜波抑制領域中,與傳統的海雜波抑制算法,如基于子空間分解的奇異值分解(SVD)算法[11-12]和基于時域對消的自適應雜波抑制算法[13]比較,運用經典的神經網絡模型同樣可以產生較好的抑制效果,如基于AlexNet的自適應雜波智能抑制方法[14]。
在人工智能領域,Joan Bruna等在卷積神經網絡(CNN)的基礎上提出了應用于圖結構的圖卷積網絡(GCN)[15],使得圖結構的特征分析越來越多地用于傳統圖像的處理中。Aditya Grover等在詞向量的數據處理算法word2vec[16]基礎上提出了應用于圖結構中的數據處理算法node2vec,該算法通過學習圖結構的特征構造出高維的節點特征向量,完成了節點分類和鏈路預測等任務[17]。
本文分析了海雜波的非平穩特性,發現了其時頻譜與目標回波信號的時頻譜之間具有明顯的結構特征區別。因此,提出基于圖特征學習的海雜波抑制算法,將雷達接收信號的時頻譜構造成圖結構的形式,并采用node2vec算法對圖進行圖嵌入處理,使用K-means聚類算法將圖嵌入的節點特征向量分類,實現在時頻域中海雜波和目標回波信號的分離,從而抑制了雷達接收信號中的海雜波分量。最后進行算法的仿真以及實測數據對比實驗,分析了該算法在不同超參數情況下的節點分類結果以及海雜波抑制效果,并給出了適合工程化應用的研究方向。
1 雷達接收信號模型
如圖1所示,機載或艦載雷達對海上目標進行監視或檢測時,海雜波會嚴重惡化雷達探測性能,此時雷達的接收信號r(t)可以表示為三部分:
r(t)=s(t)+x(t)+n(t)
(1)
式中:s(t)為目標回波信號;x(t)為海雜波回波信號;n(t)為復高斯白噪聲。海雜波的抑制問題就是在不損失目標回波信號s(t)的情況下,最大程度地抑制雜波信號x(t),提高信雜比(SCR)。

圖1 海洋雷達探測示意圖Fig.1 Schematic diagram of ocean radar detection
經過基本的雷達信號處理后,海上目標的回波信號s(t)可描述為等效復基帶形式
(2)
式中:K為目標個數;a(k)為第k個目標回波信號的雷達散射截面(RCS);fd(k)為第k個目標的多普勒頻率。
為了在海雜波干擾下有效地提取目標信息,采用STFT對雷達接收信號做預處理。STFT是典型的線性時頻變換,其計算簡便且不存在交叉項干擾的問題[18],定義為
(3)
式中:y(·)為初始信號;STFTy(t,f)表示針對y(·)信號的短時傅里葉變換;g(·)為窗函數,上標*為復共軛。對式(1)兩邊同時進行STFT,可以得到
STFTr(t,f)=STFTs(t,f)+STFTx(t,f)+STFTn(t,f)
(4)
式中:STFTr(t,f)、STFTs(t,f)、STFTx(t,f)、STFTn(t,f)分別表示針對r(t)信號、s(t)信號、x(t)信號和n(t)信號的短時傅里葉變換。
2 基于圖特征學習的海雜波抑制算法
2.1 時頻譜的圖構造
對于雷達接收信號中的目標回波信號和非平穩的海雜波信號,在經過STFT后均可以在時頻譜中表現出頻率隨時間變化的規律,且兩者的時頻譜在頻率上均是連續的。
通過對雷達接收信號的時頻譜分析,可以發現海雜波與目標回波信號時頻譜中的能量均主要分布在低頻部分,但由于海雜波的非平穩特性與目標回波信號的確定性,導致兩者在時頻譜中的能量分布情況存在著較大的結構特征差異,具體表現為:目標回波信號的能量分布比海雜波的能量分布更為集中與連續。這里將離散分布的海雜波時頻譜描述為結構相似性,將集中分布的目標回波信號時頻譜描述為社群相似性。
因此,雷達接收信號的時頻譜具有圖的結構形式,可以進行圖構造處理。將其時頻譜STFTr(t,f)進行圖構造的步驟如圖2所示。

圖2 時頻譜的圖構造流程
Fig.2 Graph construction flow of time spectrum
時頻譜的圖構造具體過程為:
步驟1提取式(4)中雷達接收信號時頻譜STFTr(t,f)圖像中的像素點,構造成二維初始矩陣S,大小為r×c。將時頻譜轉換為矩陣的形式,便于進行后續的算法處理。矩陣S表示為
(5)
步驟2設定閾值λ,記矩陣S中元素的最大值為sm(即第m個元素為最大值),對于矩陣S中的任意元素si,j,若si,j/sm<λ,則將si,j的值更新為0。記更新后的矩陣S中非0元素的個數為N。將矩陣中較小的元素賦值為0,以有利于降低矩陣的冗余度和算法的時間復雜度。此時矩陣S表示為
(6)
式中:為簡化描述,設置初始矩陣S中任意r×c-N個元素為0。
步驟3將矩陣S中為0的元素不變,其余N個非0元素重新賦值。具體的賦值方法為按照元素的下標順序,進行從1-N的連續遞增的整數賦值。圖結構中最重要的是節點之間的位置關系,使用連續遞增的整數賦值代替原本矩陣中的非0元素,便于進行圖結構中的節點關系表征。賦值更新后的矩陣S表示為
(7)
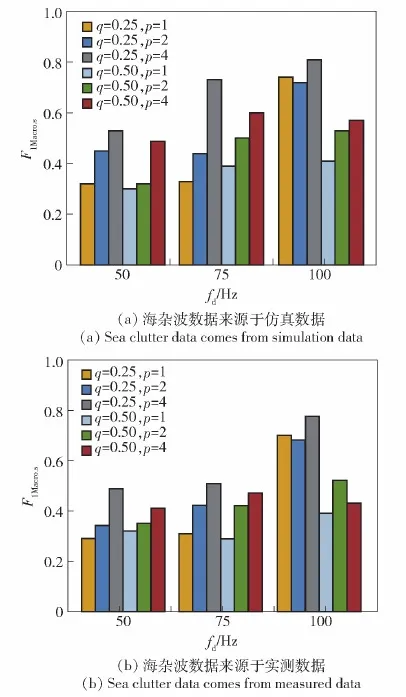
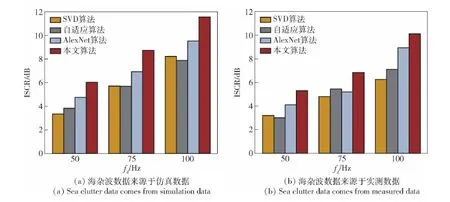
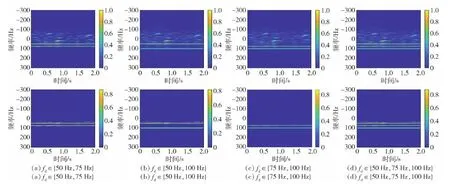
式中:4 步驟4此時矩陣S中有N個非0的連續元素值,將這N個元素看作圖結構中的N個不同節點,根據N個不同節點在矩陣S中的位置關系,構造出相對應的圖結構的鄰接矩陣Ar。 具體構造過程為:對矩陣S進行遍歷,每次所遍歷的區域大小為m×m,將遍歷區域記作Q,其余區域記作Q′,則矩陣S在遍歷過程中由Q和Q′組成,將遍歷的移動步長設置為1。在每一步遍歷中,將區域Q中節點之間的關系視為相關節點,區域Q中節點與區域Q′中節點之間的關系視為無關節點。在鄰接矩陣Ar中,將相關節點之間的權重設置為1,無關節點之間的權重設置為0,進而構造出大小為N×N的鄰接矩陣Ar。采取遍歷矩陣的方式,可以將m×m范圍內的節點看作是結構相似的,從而達到通過構造鄰接矩陣Ar來表征雷達接收信號時頻譜中不同節點之間結構位置關系的目的。 圖3 遍歷矩陣S的范圍和所對應的鄰接矩陣ArFig.3 The range of the traversal matrix S and the corresponding adjacency matrix Ar 為簡化描述,設置m=2,圖3為依次遍歷矩陣S中前4個2×2的范圍后得到相對應的鄰接矩陣Ar。對矩陣S以步長大小為1向右繼續移動遍歷,到達每行的末端時會向下移動1行,再從行首繼續以相同的方式遍歷,直到遍歷完成整個矩陣S。 步驟5通過步驟1~步驟4,可以得到式(4)中雷達接收信號的時頻譜STFTr(t,f)對應的鄰接矩陣Ar。通過Ar得到該信號的時頻譜對應的無向圖Gr,表示為 Gr=(Vr,Er,Wr) (8) 式中:Vr={vr1vr2vr3…vrN}為圖Gr中的所有節點集合;每兩個節點之間可能會存在邊;Er為這些邊的集合;Wr為每條邊上的權重共同構成的權重矩陣。這里只畫出圖3中鄰接矩陣Ar對應的圖Gr,如圖4所示。 圖4 鄰接矩陣Ar對應的圖GrFig.4 Graph Gr of adjacency matrix Ar 圖嵌入是用來挖掘圖的結構特征的方法。node2vec是一種典型的圖嵌入算法,該算法建立在傳統隨機游走策略[19-20]基礎上,結合了廣度優先搜索(BFS)和深度優先搜索(DFS)兩種圖結構的搜索策略,是一種帶有偏置的隨機游走策略,可以更加有效地檢索分散的相鄰節點[21]。 圖4所示的圖Gr中,演示node2vec算法中BFS和DFS的搜索策略,結果如圖5所示。 圖5 針對節點n2的兩種搜索策略(步長k=3)Fig.5 Two search strategies for nodes n2(step k=3) 在圖5中,如果從節點n2出發,當步長k=3時,采用BFS進行搜索所得到的節點集合是{1,n1,n3};采用DFS進行搜索所得到的節點集合是{2,3,4}。從圖5中可以發現,海雜波信號的時頻譜STFTx(t,f)的像素點呈現出的結構相似性與BFS的搜索策略是一致的,而目標回波信號的時頻譜STFTs(t,f)的像素點呈現出的社群相似性與DFS的搜索策略是一致的。因此,node2vec算法可以對由雷達接收信號的時頻譜所生成的無向圖進行圖嵌入處理,使用高維向量表征每個節點,對同一種信號節點之間的相似程度以及不同信號節點之間的差異程度進行描述。 在node2vec算法中,有兩個重要的超參數p和q,下面解釋這兩個超參數的作用。 圖4所示的圖Gr中,演示node2vec算法的隨機游走搜索策略:當從節點1到達節點n2后,評估離開節點n2時對下一個即將到達的節點的搜索策略,具體如圖6所示。 圖6 隨機游走的搜索策略Fig.6 Random walk search strategy 圖6中,α為隨機游走的搜索偏置,也可以被看作是從節點n2到下一個節點的轉移概率,其取值范圍為 (9) 式中:l1x表示節點1和節點x之間的最短距離,這里的節點x是指圖6中的節點1、節點2、節點n1和節點n3。 可以發現,轉移概率α受到超參數p和q的影響,因此超參數p和q的作用是調節隨機游走的搜索策略走向,對其具體的理解為: 1)超參數p控制著再次訪問已訪問節點的概率(返回節點1),超參數q控制著遠離已訪問節點的概率(走向節點2或者節點n3); 2)p的值越小,隨機游走的策略傾向于回溯節點1,當p的值越大,隨機游走的策略將更接近DFS,傾向于不回溯節點1,降低了2-hop的冗余度; 3)q的值越小,隨機游走的策略將更接近DFS,q的值越大,隨機游走的策略將更接近BFS[22]。 因此,通過調節node2vec算法中的超參數p和q,可以控制隨機游走序列中下一個節點的選擇。超參數p和q的引入使得BFS和DFS可以交互存在,進而實現不同特性的搜索策略,得到適合本文中圖Gr所對應的圖結構搜索方式。 通過使用node2vec算法,將圖Gr中的每個節點實現由低維度向高維度的映射,進而得到每個節點的高維特征向量。將node2vec算法的映射關系記作f,映射過程可以表示為 f:Vr→V′rvri=[i]→v′ri=[v′ri1v′ri2…v′rid] (10) (11) 式中:Vr和V′r分別表示圖Gr映射前后的節點集合;vri和v′ri分別為在圖Gr中映射前后的任意一個節點;d為維度為d的高維空間中的全體實向量集合。 可以發現,在進行圖嵌入前,節點集合Vr中節點之間的相關性只能通過鄰接矩陣Ar來表示,每個節點本身沒有攜帶任何信息;在進行圖嵌入后節點集合V′r中的每個節點都使用了d維向量進行表征,此時可以采用詞向量數據處理算法word2vec[16]中衡量向量相似度的方法來分析節點之間的相關性,計算方法如下: (12) 式中:D(v′ri,v′rj)為節點集合V′r中任意兩個節點v′ri和v′rj之間的歐式距離;u用來衡量節點之間的相似度,范圍為[0,1],取值越大,表明節點之間的相似度越大。 通過式(12)中節點之間的相似度u,可以得到雷達接收信號時頻譜中的像素點在經過圖嵌入處理后的相關性,依據相關性的大小,可以采用K-means聚類算法,將經過圖嵌入處理后圖Gr中的節點進行分類。這里將式(10)中的節點集合V′r劃分成n類,表示為 (13) 式中:V′s表示目標回波信號的節點集合;V′x表示海雜波的節點集合。在圖Gr中,目標回波信號中同一多普勒頻率對應的節點是集中連續的,其節點之間的相似度u較大,通過K-means聚類算法會將這些節點劃分為一類。根據式(2),目標回波信號中有K個不同的多普勒頻率分量,因此V′s是由K個節點集合構成的,V′x是由剩下的n-K個節點集合構成的。 節點集合V′r中的N個節點是與式(6)中矩陣S中的N個非0元素一一對應的,因此V′s和V′x也各自對應著矩陣S中的部分非0元素,矩陣S可以表示為 S=Ss+SxV′s→SsV′x→Sx (14) 式中:矩陣Ss表示目標回波信號的時頻譜對應的像素點矩陣;矩陣Sx表示海雜波信號的時頻譜對應的像素點矩陣,由此可以對式(4)中雷達接收信號的時頻譜STFTr(t,f)進行分離,得到其中的STFTs(t,f)部分和STFTx(t,f)部分,再去除STFTx(t,f)部分,就完成了在時頻域上對雷達接收信號中海雜波回波信號分量的抑制。 圖7 海雜波抑制算法Fig.7 Sea clutter suppression algorithm 因此,本文所提基于圖特征學習的海雜波抑制算法的流程圖(見圖7)主要包括4個步驟: 1)對目標回波信號和海雜波信號數據進行STFT,得到時頻譜; 2)對時頻譜進行圖構造處理,得到對應的鄰接矩陣Ar和圖Gr; 3)使用node2vec算法,對鄰接矩陣Ar進行圖嵌入處理; 4)使用K-means聚類算法,依據圖Gr中節點的特征向量進行節點分類,實現海雜波的抑制。 本文算法的參數主要由3個部分組成: 1)目標回波信號中的目標個數K,多普勒頻率分量的取值集合fd,采用基于實測數據的海雜波建模方法[23-24]生成海雜波的仿真數據時需要設置尺度參數和形狀參數; 2) node2vec算法中的超參數p和q,節點特征向量的維度d,隨機游走的次數r; 3) K-means聚類算法中的分類參數n。 具體的仿真參數設置如表1所示。 表1 仿真參數設置Table 1 Simulation parameter setting 本文將超參數p的取值集合設置為{1,2,4},將超參數q的取值集合設置為{0.25,0.50},主要有兩方面原因: 1)為減少在隨機游走的過程中對同一個節點重復回溯的搜索行為,降低node2vec算法的冗余度,因此超參數p需要較大的取值; 2)通過分析本文需要進行圖嵌入操作的圖結構特征,可以發現目標回波信號節點之間的有序性要遠大于海雜波節點之間的有序性,因此目標回波信號節點之間的結構關系更容易被探索,且目標回波信號時頻譜的結構表現為社群相似性,故本文的node2vec算法需要更傾向于DFS的搜索策略,超參數p需要較大的取值,超參數q需要較小的取值。 本文主要對node2vec算法、K-means聚類算法以及雷達接收信號中海雜波分量的抑制效果這3個方面進行評價。 1)對node2vec算法的有效性進行評價 計算雷達接收信號中目標回波信號節點之間的相似度平均值u1和目標回波信號節點與海雜波節點之間的相似度平均值u2,通過比較u1和u2的大小,可以表明node2vec算法所構造的特征向量的有效性。 2)對K-means聚類算法的有效性進行評價 將目標回波信號對應的節點作為正類節點,將海雜波回波信號對應的節點作為負類節點,則本文的節點分類問題本質上是一個二分類問題。針對本文的二分類模型,定義F1分數對其進行性能衡量,計算公式為 (15) 式中:P為分類模型的精確率;R為分類模型的召回率;TP表示將實際類別是正類的節點預測為正類的節點數目;FP表示將實際類別是負類的節點預測為正類的節點數目;FN表示將實際類別是正類的節點預測為負類的節點數目。 F1分數可以具體分為宏觀F1分數F1Macro,s和微觀F1分數F1Micro,s,計算公式分別為 (16) 式中:F1T和F1N分別表示正類和負類的F1分數。從二者的計算方式上可以看出,宏觀F1分數是平等地看待各個類別,它的值會受到稀有類別的影響;微觀F1分數則更容易受到常見類別的影響。宏觀F1分數和微觀F1分數的取值范圍均為[0,1],取值越大,則表明分類的效果越好。 因此,本文采用F1Macro,s和F1Micro,s對K-means聚類算法的有效性進行評價。 3)對雷達接收信號中海雜波分量的抑制效果進行評價 根據2.3節,在時頻域中可以分別得到經過分類模型處理后的目標回波信號功率和海雜波回波信號功率。為了衡量本文算法對雷達接收信號中海雜波分量的抑制效果,提出了信號雜波比(SCR)的改善因子ISCR(ISCR)[25],定義為 ISCR=SCRo-SCRi (17) 式中:SCRi和SCRo分別表示使用本文的海雜波抑制算法處理雷達接收信號前后的信雜比。 用于驗證本文海雜波抑制算法的海雜波數據有以下兩個來源: 1)仿真數據:采用基于實測數據的海雜波建模方法,所生成的100組海雜波仿真數據進行仿真驗證; 2)實測數據:采用海雜波實測數據[24],取第1 000個距離單元至1 100個距離單元的100組海雜波實測數據進行仿真驗證。 將集合fd中的多普勒頻率分量進行組合,得到表1中K在不同取值時的目標回波信號,分別添加至仿真數據和實測數據中。在K取值為1、2和3時,雷達接收信號的平均SCR分別為-15 dB、-12 dB和-9 dB。 本節將通過對超參數p和q的優化,時頻譜的直觀結果對比以及本文算法與現有算法的對比這3個方面進行仿真與實測結果的分析。 從3.1節中算法參數的設置可以看出,超參數p和q的取值是一個集合,因此首先需要通過仿真結果的評價指標選取本文算法中的最優超參數p和q。 首先,對K=1時的單目標環境進行仿真分析。使用node2vec算法進行圖嵌入處理后所得節點向量之間的相似度u1和u2對比情況如表2和表3所示。從表2和表3中可以發現:當多普勒頻率相同時,在不同的超參數情況下,相似度u1的值均遠大于u2,因此使用node2vec算法所構造的特征向量可以將兩種信號的節點進行有效區分;當超參數{p,q}={4,0.25}時,可以同時取到相似度u1的最大值和相似度u2的最小值,表明此時兩種信號節點之間的區分度最大。 在3種多普勒頻率下,圖8和圖9為使用K-means聚類算法后得到的仿真結果F1Macro,s和F1Micro,s。可以發現,二者均是超參數{p,q}={4,0.25}時取得最大值,表明此時得到了最好的分類效果。圖10為使用本文海雜波抑制算法前后的ISCR對比圖。由圖10可以發現,當超參數{p,q}={4,0.25}時,雷達接收信號的信雜比得到了最大提升,其中仿真數據的ISCR和實測數據的ISCR最高可分別達到11.59 dB和10.13 dB。 表2 海雜波數據來源于仿真數據Table 2 Sea clutter data comes from simulation data 表3 海雜波數據來源于實測數據Table 3 Sea clutter data comes from measured data 圖8 Macro-F1 scoreFig.8 Macro-F1 score 圖9 Micro-F1 scoreFig.9 Micro-F1 score 通過對上述3種評價指標的分析,均是在超參數為{4,0.25}時取得了最好的分類效果,因此本文算法的最優超參數選取為{p,q}={4,0.25}。 圖10 ISCRFig.10 ISCR 在3種不同的多普勒頻率下,取最優超參數時,使用本文的海雜波抑制算法處理實測海雜波數據的時頻譜如圖11所示,其中第1行圖片是使用抑制算法前雷達接收信號時頻譜,第2行圖片是使用抑制算法后從雷達接收信號中所分離出的目標回波信號時頻譜。由圖11可以發現,在單目標環境下,本文的海雜波抑制算法可以實現在時頻域上進行雷達接收信號中海雜波分量的抑制。 設置本文算法的超參數為最優超參數的情況下,與SVD算法、自適應雜波抑制算法和基于AlexNet的自適應雜波智能抑制方法進行仿真比較,得到的ISCR對比結果如圖12所示。 由圖12可以看出,針對上述兩種不同來源的海雜波數據,本文算法的ISCR均優于其他3種算法,進一步驗證了該算法的有效性。 對K=2和K=3時的多目標環境進行上述相同的仿真分析,得到的最優超參數均為{p,q}={4,0.25}。再使用本文的海雜波抑制算法處理實測海雜波數據的時頻譜如圖13所示,其中第1行圖片是雷達接收信號的時頻譜,第2行圖片是從雷達接收信號中分離出的目標回波信號的時頻譜。可以發現,在多目標環境下,本文的海雜波抑制算法同樣可以實現在時頻域上進行雷達接收信號中海雜波分量的抑制。 圖11 單目標環境下使用海雜波抑制算法前后的時頻譜對比Fig.11 Time spectrum comparison before and after sea clutter suppression algorithm in single target environment 圖12 4種算法進行海雜波抑制后的ISCR對比Fig.12 Four algorithms are used to compare ISCR after sea clutter suppression 圖13 多目標環境下使用海雜波抑制算法前后的時頻譜對比Fig.13 Time spectrum comparison before and after sea clutter suppression algorithm in multiple target environment 本節在單目標和多目標的環境下,分別對兩種不同來源的海雜波數據下的雷達接收信號模型進行算法的仿真分析。首先對比在不同超參數情況下的分類效果,得出了最優超參數的取值集合;然后在最優超參數下,使用本文的海雜波抑制算法處理實測海雜波數據,從時頻譜的角度驗證了本文算法的可行性;最后將本文算法與其他3種算法進行分析對比,進一步驗證了本文算法對抑制雷達接收信號中海雜波回波信號分量的有效性。 通過對雷達接收信號時頻譜的結構分析,將圖特征學習的理論引入到海雜波的抑制領域中。本文通過對時頻譜的圖嵌入和分類算法,實現了雷達接收信號中海雜波分量的有效抑制,同時驗證了圖論方法應用于海雜波處理中的可行性。新算法流程直觀簡單,但需要進行時間復雜度較高的海雜波數據的圖構造處理,因此在后續的研究中需要進一步優化數據預處理環節。

2.2 基于node2vec的圖嵌入算法


2.3 基于K-means的節點分類算法

3 仿真與實測結果及分析
3.1 參數設置

3.2 評價指標
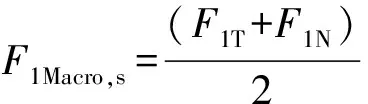
3.3 仿真與實測結果分析





4 結論

