艦艇編隊反導作戰中質心干擾運用策略研究

吳賜聰，于 瑩，程志鋒

(海軍工程大學,湖北 武漢 430033)

0 引 言

現代海戰中，反艦導彈由于其射程遠，精度高，威力大，一直是水面艦艇面臨的主要威脅。當受到導彈末制導雷達跟蹤時，艦艇實施質心干擾是有效的反導手段之一。實際運用中，單艦艇使用質心干擾可以達到較好的反導自衛效果；但編隊條件下，使用質心干擾就很容易出現由于目標艦艇質心干擾不當而導致鄰艦受到導彈二次威脅的情況。因此，艦艇編隊使用質心干擾需滿足一定條件，也就是編隊質心干擾運用策略。

1 艦艇質心干擾引偏效果分析

當受到導彈威脅時，艦艇使用質心干擾會使導彈末制導雷達分辨單元內存在2個或2個以上的目標，進而使導彈轉向跟蹤由這數個目標共同構成的能量中心(質心)，從而偏離艦艇方向[1]。干擾效果越好，則偏離角度越大。因此，理論上存在使導彈偏離角度最大的質心干擾發射角度[2-3]。

現建立三維直角坐標系，分析質心干擾最佳發射角度，如圖1所示。

圖1中，O、M′、T′分別表示艦艇、箔條云、導彈。O為坐標原點；λ表示導彈入射舷角；|OT′|=a0表示艦艇發現導彈時導彈與艦艇之間的距離；|OM′|=r0表示質心干擾的布放距離；D′表示艦艇O和箔條云M′的質心點；|OD′|=d0表示艦艇到質心點的距離。艦艇航向與y軸方向同向。α0為發射箔條彈的舷角(簡稱“發射舷角”，下同)；θ0為導彈空間引偏角。

為便于計算和判斷，將以上三維空間場景投影到水平面，M、T分別為箔條云和導彈在平面上的投影，平面圖如圖2所示。

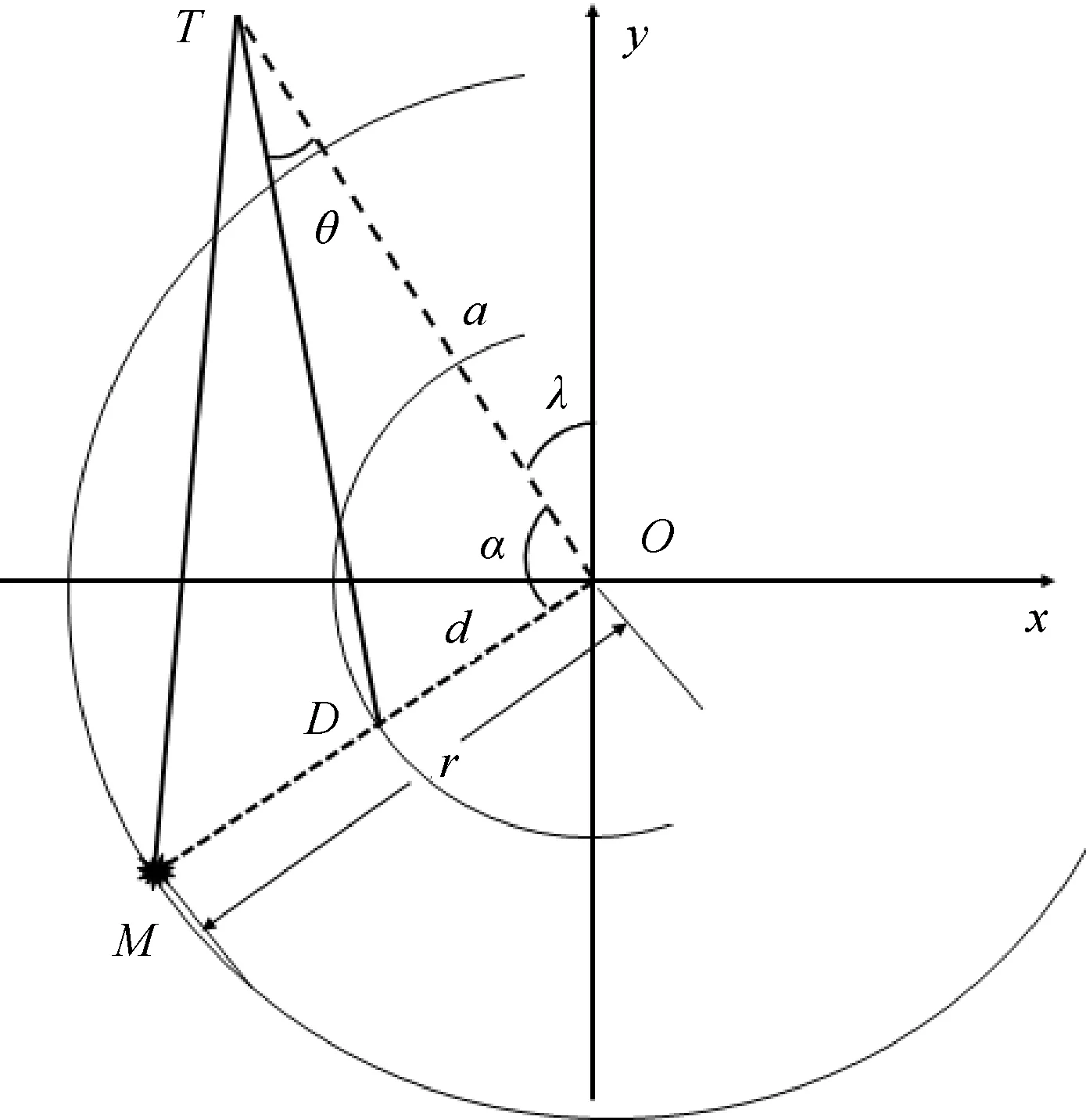
圖2 質心干擾布設平面圖

圖2中，|OT|=a表示導彈發現艦艇并開始跟蹤時導彈與艦艇之間的水平距離(簡稱“跟蹤距離”，下同)；|OM|=r表示質心干擾的布放水平距離；D為質心點D′的投影；|OD|=d表示艦艇到質心點的水平距離(簡稱“質心距離”，下同)；θ0在水平面上的投影為θ(稱為“引偏角”，下同)。α為由導彈入射方向轉向箔條彈發射方向的夾角(簡稱“發射夾角”，下同)。由圖1、圖2可見，由于空間上的θ0與平面上的θ具有相關變化關系，并且實戰中導彈一般都是低空掠海飛行，其高度遠小于其跟蹤距離，高度對θ計算結果的影響很小，所以投影到水平直角坐標系進行簡化討論是可行的。

任意時刻，若導彈已經發現并跟蹤艦艇，則表示艦艇和導彈雷達均能發現對方，此時距離a可確定。當質心干擾樣式確定時(布放距離、數量等)，艦艇到質心點D的距離即質心距離d也可確定。由此，在ΔOTD中，有：

(1)

可計算得出引偏角為：

(2)

1.1 不同質心距離下的引偏效果

設跟蹤距離a=20 km,當質心距離d分別取0.5 km、1.0 km、1.5 km時，可得發射夾角α與引偏角θ的關系，如圖3所示。

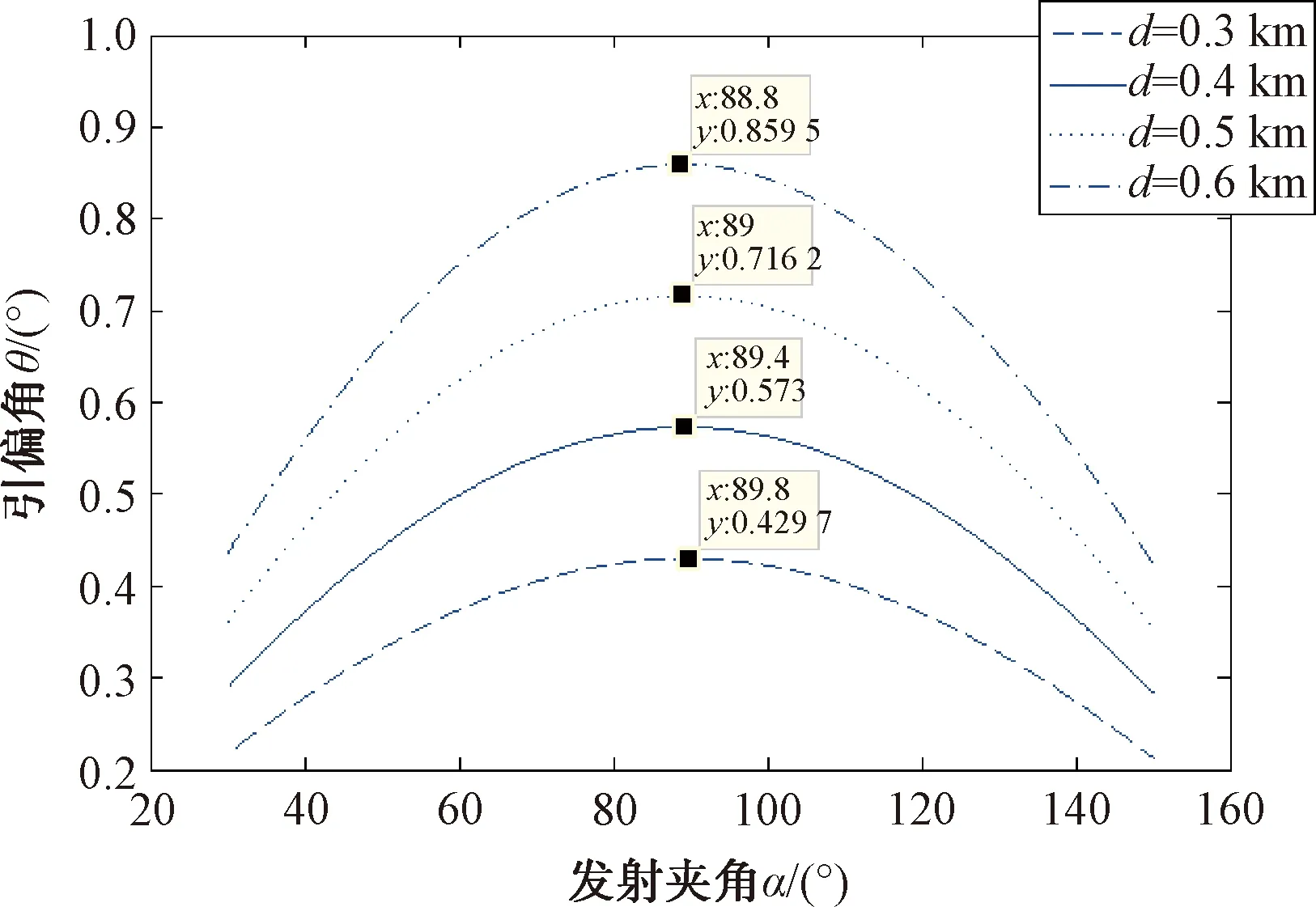
圖3 不同質心距離時干擾發射夾角與引偏角關系圖

由圖3可見，質心距離d一定時，發射夾角α在70°～ 110°之間都有較好的引偏效果，最佳發射夾角在80°～ 90°之間，此時引偏角θ最大，即引偏效果最好；質心距離d取值不同的情況下，d越大，引偏效果越好。為便于描述，在此定義αe為最佳發射夾角，即在其他條件固定，僅有發射夾角α變化時，使得θ值最大的α(下同)。

1.2 不同跟蹤距離下的引偏效果

設導彈的跟蹤距離a分別為10 km、20 km、30 km、40 km,取質心距離d=1.0 km，可得發射夾角α與引偏角θ的關系，如圖4所示。

圖4 不同跟蹤距離時發射夾角與引偏角關系圖

由圖4可見，導彈跟蹤距離a越大，相同條件下引偏角θ越小，使得引偏角θ取最大值的發射夾角α也越大。

2 艦艇實施質心干擾對鄰艦的影響

實際上，在編隊作戰時，使用質心干擾必須要考慮對鄰艦的影響。在此，假設編隊內各艦艇具有同等重要性，如驅逐艦編隊或驅護編隊，而不存在優先被保護艦艇。

一般來說，某一艦艇發射箔條彈后，必定會出現這種情況：導彈末制導雷達波束內同時存在艦艇和箔條云，使得導彈由于質心效應而偏離原方向并向質心飛行。這種情況下，導彈可能會直接穿過質心，其末制導雷達波束鎖定后方艦艇，或開啟搜索雷達進行二次搜索。下文討論即圍繞此種情況展開。

質心干擾的釋放時機是在導彈完成末制導搜索之后的跟蹤階段，這一階段導彈與艦艇的距離通常不超過20 km，艦艇沒有足夠的時間機動，質心干擾對導彈的引偏角度一般較小，難以使導彈飛行方向徹底偏離整個編隊。對于艦艇編隊而言，一般在來襲導彈同側實施質心干擾才可能有效引偏導彈(特別地，對于編隊最前或最后的艦艇，發射與導彈異側舷的箔條彈引偏效果更好)，但同時存在導彈穿過質心點威脅編隊其他艦艇的可能性。

艦艇編隊基本戰斗隊形包括單縱隊、單橫隊、方位隊列、人字隊列、菱形隊列、環形隊列等。本文選擇其中有代表性的方位隊列、人字隊列進行討論。圖5、圖6給出了方位隊列、人字隊列下質心干擾引偏導彈后威脅鄰艦的情況。

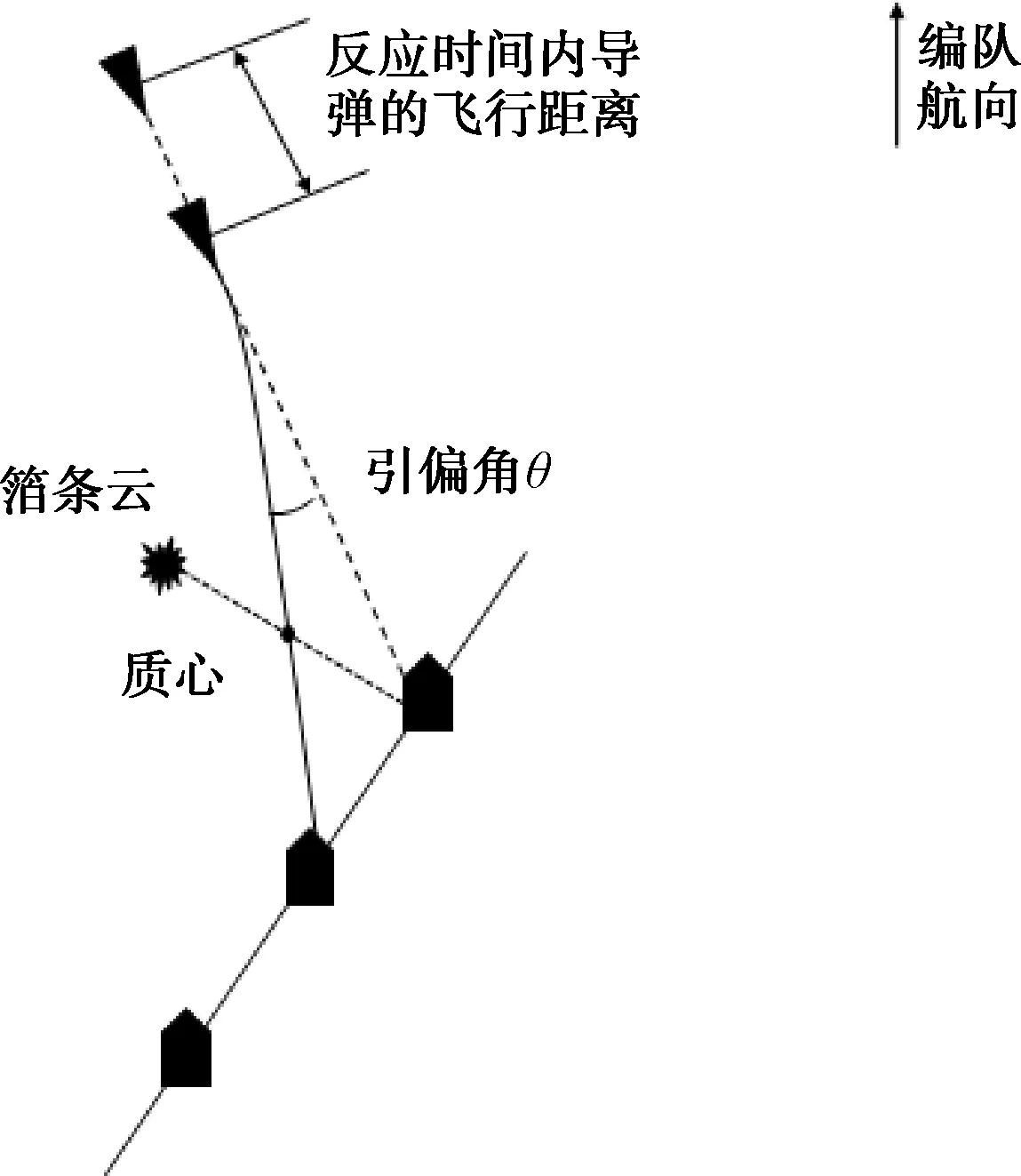
圖5 方位隊列下質心干擾導致鄰艦被攻擊示意圖

3 艦艇實施質心干擾時避免對鄰艦產生影響的策略

下面分別討論在方位隊列、人字隊列下，艦艇實施質心干擾如何避免對鄰艦造成威脅。

3.1 方位隊列下的質心干擾策略

方位隊列時，導彈可能被引偏飛向同側鄰艦，如圖7所示。在該平面直角坐標系中，A、B、C分別表示方位隊列下的3艘艦艇，T為來襲導彈，M為箔條云，λ表示導彈入射舷角，|AT|=a為跟蹤距離，|AM|=r表示質心干擾釋放距離，D為艦艇A和誘餌M的質心點，|AD|=d為質心距離，α為發射夾角，θ為引偏角，以上設置與前述相同。設|AB|=|AC|=b表示艦艇間距，β角為導彈被引偏后，其飛行方向與DB(質心點和后方艦艇連線)的夾角。

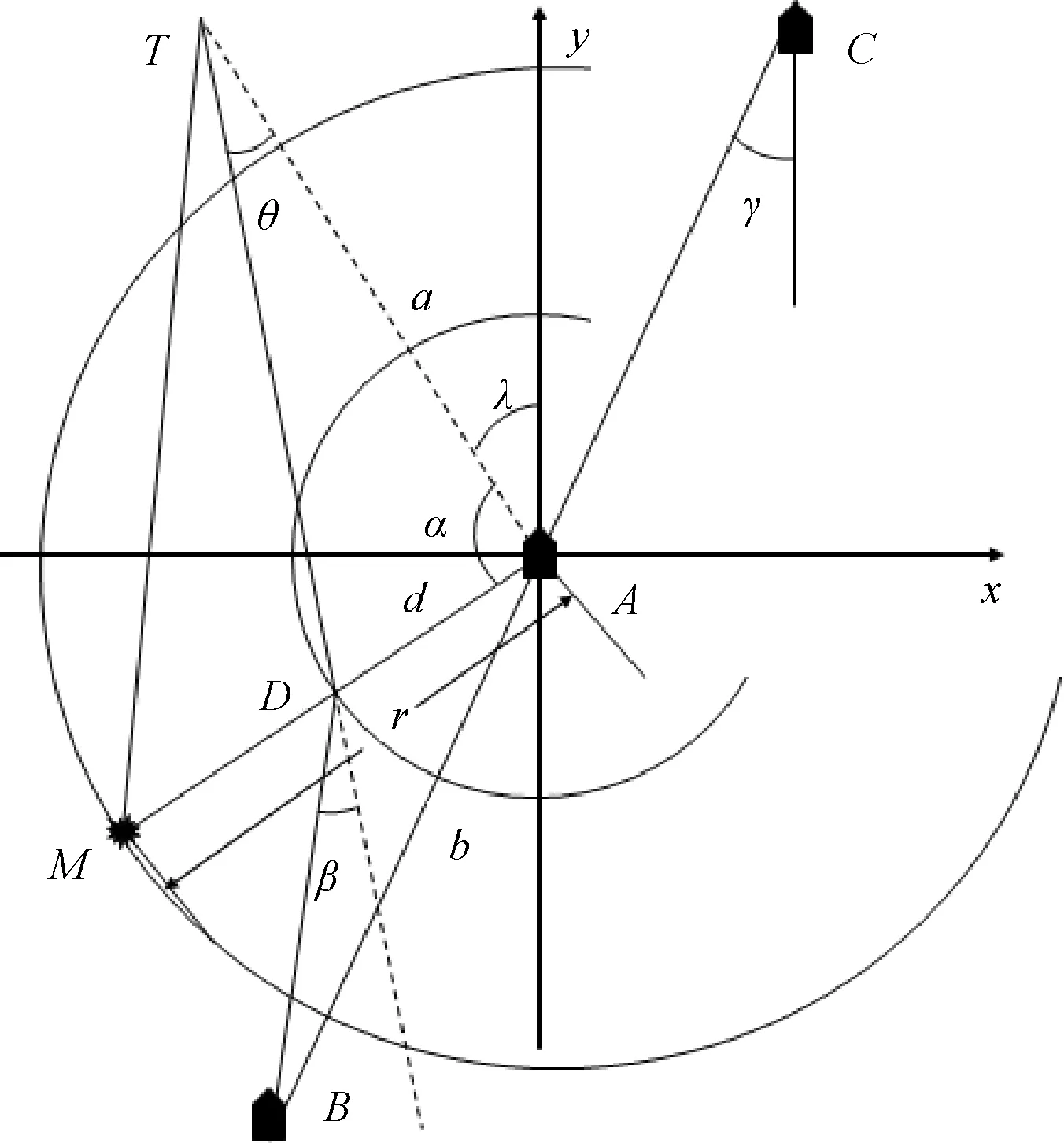
圖7 方位隊列下導彈攻擊鄰艦平面圖

圖7中，ΔABD具有如下角關系：

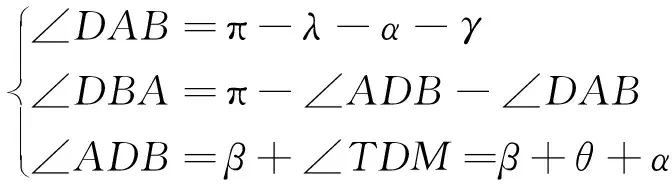
(3)

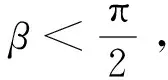
若艦艇使用與來襲導彈同側的干擾彈，應滿足λ+α+γ<π，否則質心干擾將在來襲導彈異側舷發射，對導彈的引偏效果變差，導致目標艦艇自身容易受到導彈威脅。同時，30°<α+λ<150°，否則艦艇武器裝備系統不能滿足箔條彈發射需要(發射管旋轉角度限制)。

利用正弦定理，在△ABD中得到如下關系式：

(4)

由式(3)和(4)計算得到β關于α的關系式：

(5)

式中：θ的算法同式(2)。

由式(5)可計算目標艦艇發射箔條彈方向的限制條件。

現假設跟蹤距離a=20 km，艦艇編隊隊列角γ=30°，質心距離d=0.5 km，艦艇間距b=5 km，箔條彈允許覆蓋的發射角度范圍為30°～150°舷角。導彈入射舷角λ分別取30°、45°、60°、90°、120°時，計算可得β值，如圖8所示。

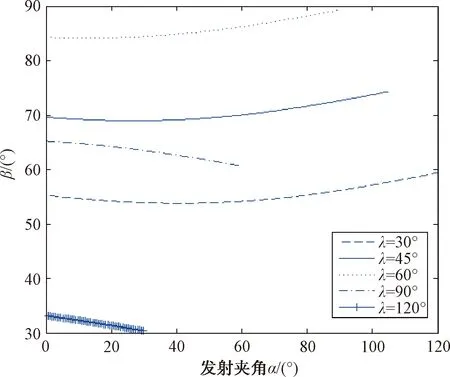
圖8 入射舷角不同時導彈對鄰艦的威脅隨發射夾角變化圖

由圖8可分析得到如下結論：

(1) 當導彈入射舷角小于90°時，箔條彈的發射夾角α越大，越不容易使導彈威脅鄰艦。但此時使得鄰艦受威脅最小的發射夾角α與1.1節所述最佳發射夾角αe并不重合。因此，應兼顧導彈引偏效果保證目標艦艇安全的同時，盡可能減小對鄰艦的威脅。在這2個要求下，發射夾角應根據實際情況來確定：當導彈入射舷角較小時，發射夾角α取值范圍在80°～100°之間時，綜合效果較好；當入射舷角較大但不超過90°時，發射夾角α應盡可能接近最佳發射夾角αe。

(2) 當導彈入射舷角大于90°時，發射夾角α越大，鄰艦受到的威脅越大，其原因是此時效果較好的發射舷角α0將小于入射舷角λ。這種情況下，可能受到導彈二次威脅的艦艇變為C艦，用于判斷B艦受威脅可能性的β消失，導致結果無法計算。若要繼續判斷C艦受威脅的可能性，則需重新計算角度關系，計算方法與前述方法相似，故不贅述。

(3) 假設導彈的跟蹤波束范圍為15°，由圖8可以看出，導彈以任意角度入射時，β均大于導彈的半波寬度7.5°，因此在該隊形下目標艦艇使用質心干擾幾乎不會對鄰艦造成二次導彈威脅；若導彈開啟二次搜索，其搜索波束范圍為120°，在導彈以小于45°舷角入射時，存在β小于半波寬度60°的情況，目標艦艇進行質心干擾可能導致鄰艦受到二次導彈威脅，需要鄰艦同時采取導彈抗擊措施。

3.2 人字隊列下的質心干擾策略

人字隊列時，導彈可能穿過這種復式隊形的一側，擊中另一側，如圖9所示。該人字隊列左右隊列角相同，設其余條件均與3.1節的方位隊列情況下相同。圖9為人字隊列下導彈攻擊鄰艦效果圖。

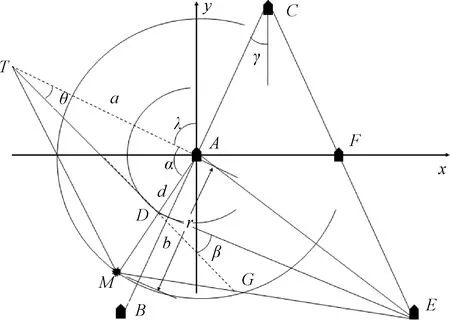
圖9 人字隊列下導彈攻擊鄰艦效果圖

據圖9可以判斷：β較大時，計算結果與3.1節結果類似，因此這里不做重復討論；β較小時，會對E艦造成威脅。β的計算式為：

β=arccos∠MDE-(π-θ-α)

(6)

式中：

(7)

△DEM、△ACE、△ADE中存在以下邊長關系：

(8)

在△ACE、△ADE中，存在以下角度關系：

(9)

式中：∠MAB>0，即α+λ+γ<π，若不滿足該條件，質心干擾將在來襲導彈異側舷發射，對導彈的引偏效果變差，導致目標艦艇自身容易受到導彈威脅；且α+λ>30°，否則艦艇武器系統不能滿足質心干擾發射需要(發射管旋轉角度限制),此部分的限制條件也與方位隊列情況下相同。

由式(6)～式(9)，求得β關于α表達式為：

(π-θ-α)

(10)

(11)

引偏角θ的計算同式(2)。

現假設導彈跟蹤距離a=20 km,艦艇編隊隊列角γ=30°，艦艇到質心點的距離d=0.5 km,艦艇間距b=5 km,箔條彈發射舷角范圍為30°～150°。導彈入射舷角λ分別取30°、45°、60°、90°、120°，計算可得β值，如圖10所示。

由圖10可分析得到如下結論：

(1) 導彈以不同入射舷角λ攻擊目標艦艇，λ較小時，發射夾角應取得范圍在80°～100°之間較好；若入射舷角較大但不超過90°時，發射夾角應盡可能接近最佳發射夾角αe。此部分結論也與3.1節類似。

(2) 當發射夾角小于90°時，發射夾角的起始值并非從0開始，這是因為此時若以一個小角度發射質心干擾，導彈引偏后受威脅的艦艇變為F艦，需重新計算角度關系。

(3) 假設導彈的跟蹤波束范圍為15°，由圖10可以看出，導彈入射舷角在60°～90°時，β小于半波寬度7.5°，即目標艦艇使用質心干擾容易對鄰艦造成2次導彈威脅；若導彈開啟2次搜索，其搜索波束范圍為120°，導彈在小于90°舷角時入射，因β均小于搜索半波寬度，可以認為必然會再次搜索到E艦；而在入射舷角大于90°時，效果較好的發射舷角α0將小于入射舷角λ，又容易導致C艦被導彈搜索跟蹤，因此需要這些艦艇同時采取導彈抗擊措施。由此可見，復雜隊形的艦艇編隊，在強化了打擊能力的同時，也增大了反導的難度，這對編隊整體的協同能力是很大的考驗。

利用公式(10)，也可以討論其他條件變化時，艦艇質心干擾的布設策略。設導彈入射角為λ=45°不變，改變隊列角γ、跟蹤距離a、艦艇間距b等參數，再按上述步驟計算β值，可以得出如下結果和結論：

(1) 跟蹤距離越大，被引偏的導彈越容易發現E艦，如圖11所示。這是因為跟蹤距離越大，導彈的雷達視野范圍越廣，導彈到A艦、E艦連線的夾角越小，那么引偏后，導彈越容易在雷達波束內發現E艦。

圖11 跟蹤距離不同時導彈對鄰艦的威脅隨發射夾角變化圖

(2) 適當增大艦艇隊列角γ，使得E艦能有效地遠離導彈雷達波束范圍，有利于避免導彈威脅，如圖12所示。

圖12 隊列角不同時導彈對鄰艦的威脅隨發射夾角變化圖

(3) 艦艇間距越大，E艦越容易進入被引偏的導彈的末制導雷達波束內，越容易受到威脅，如圖13所示。

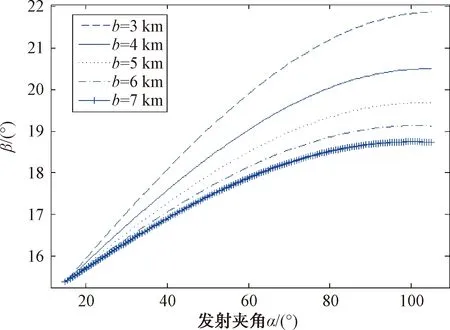
圖13 艦艇間距不同時導彈對鄰艦的威脅隨發射夾角變化圖

(4) 箔條云的雷達反射面積越大，即質心越接近云團，質心距離d越大，這種情況下對E艦威脅也越小，如圖14所示。

圖14 不同質心距離時導彈對鄰艦的威脅隨發射夾角變化圖

3.3 二次質心干擾策略

導彈被目標艦艇的質心干擾引偏后，可能對鄰艦造成威脅。這種情況下，鄰艦也可使用質心干擾(稱為二次質心干擾)，協同將導彈引偏至脫離編隊，保證編隊安全[2]。

根據3.1節的計算，方位隊列時，艦艏或艦艉方向45°范圍內入射的導彈在引偏后容易對鄰艦造成威脅。圖15所示為方位隊列艦艇編隊二次質心干擾圖。

圖15 方位隊列艦艇編隊二次質心干擾圖

對于像人字隊列這樣的復式隊列，導彈被引偏后的情況有多種，因此考慮條件較為復雜。目標艦艇同側鄰艦實施質心干擾的情形與方位隊列類似，如圖16所示。當導彈穿過編隊某一側的隊列線后，另一側的艦艇就需要視導彈來襲方向實施二次質心干擾，如圖17所示。

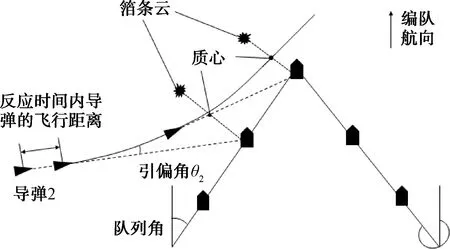
圖16 人字隊列艦艇編隊二次質心干擾圖1

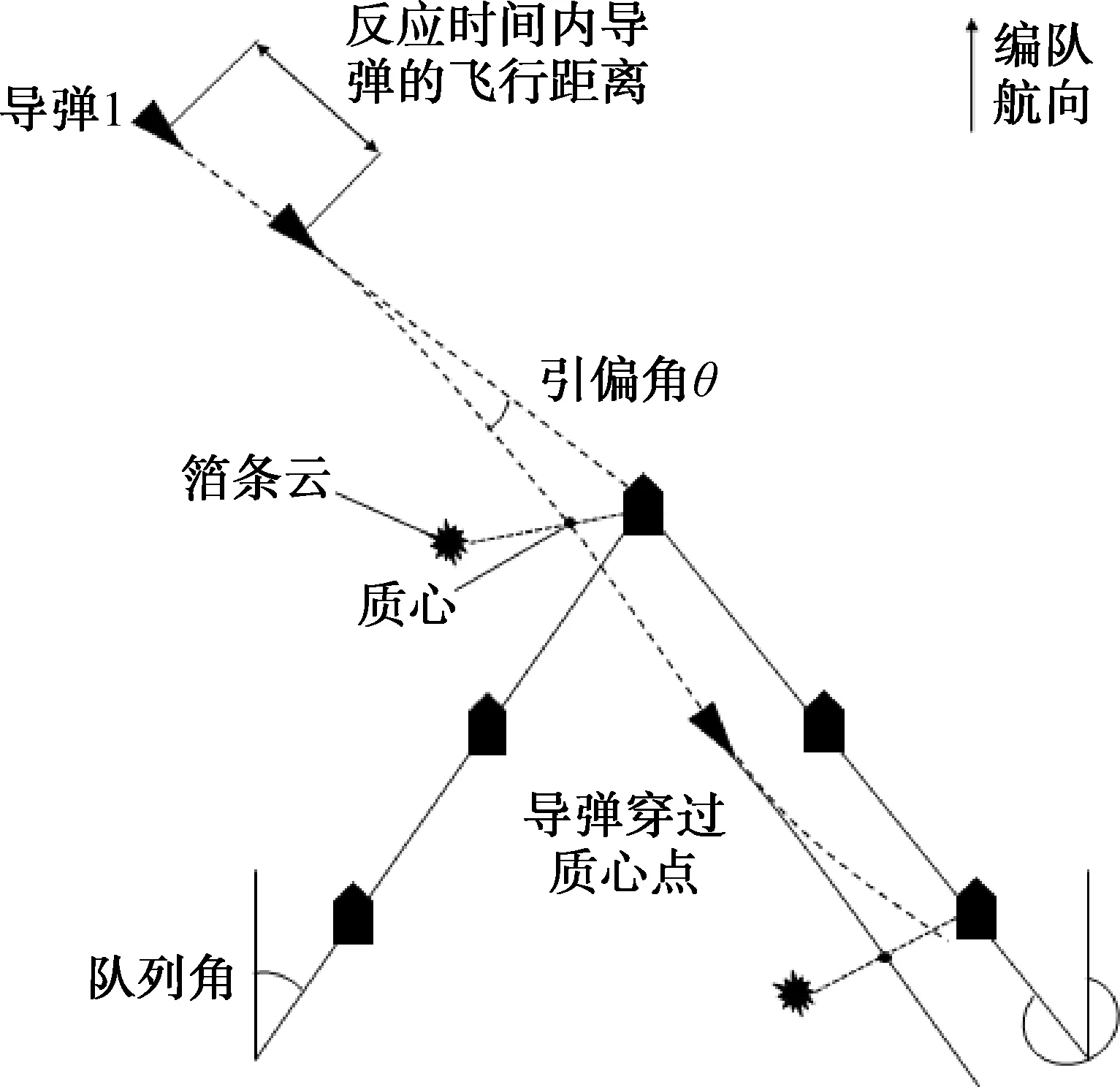
圖17 人字隊列艦艇編隊二次質心干擾圖2

4 結束語

文章旨在通過一種較為簡單的計算方法，分析導彈引偏效果，建立目標艦艇實施質心干擾與編隊受導彈二次威脅之間的關聯關系，以計算仿真的方法，通過定性和定量給出編隊質心干擾策略。計算方法較為便捷，對于艦艇編隊快速判斷威脅并擬定質心干擾策略有一定幫助。