基于數值模擬的裂縫型儲層巖石導電效率響應規律研究

＊馬庭堅

（長江大學地球物理與石油資源學院 湖北 430100）

1.引言

裂縫儲層是一種重要的油氣儲層類型，廣泛發育于致密砂巖、油頁巖、碳酸鹽巖、火山巖、變質巖等多種巖性中[1]。非常規儲層中，裂縫是重要的儲集空間和主要的滲流通道，在儲層的評價中占有重要作用，其有效性將直接影響產能[2-6]。目前，裂縫的常規測井識別主要利用深、淺雙側向電阻率幅度差異及三孔隙度測井曲線[7-9]。而成像測井識別和陣列聲波測井識別是非常規測井的主要方式，通過對成像測井的圖像處理能有效得到裂縫的定量參數，但只能反應井壁裂縫的情況，無法評價裂縫向井外延伸情況。陣列聲波測井的最大優勢是探測范圍大，利用陣列聲波測井識別裂縫能彌補成像測井識別的不足[10-11]。但其測井成本巨大，廣泛應用受到限制。

導電效率受地層非均質影響小，廣泛應用于建立碳酸鹽巖儲層飽和度模型及儲層裂縫類型的識別[12-14]。最早由Herrick等提出其定義式[15]，高楚橋等首次將其用于識別碳酸鹽巖儲層類型[16]，袁秀婷等利用測井資料計算的導電效率較好地識別塔河油田碳酸鹽巖儲集層的類型[17]。李兆平等在高楚橋提出的儲層模型上進行改進，推到了適用于復雜地層的導電效率表達式[18]。

因此本文通過數值模擬的方法對裂縫不同情況下的導電效率進行計算分析。根據數學模型，在數值模擬軟件中建立裂縫-孔洞模型。通過設置不同的裂縫寬度、裂縫傾角、孔洞大小及基巖孔隙度等參數，計算得到相應的導電效率并分析。為區分裂縫型儲層的儲集空間類型提供參考。

2.導電效率的定義及測井計算式

Herrick和Kennedy最早提出了巖石導電效率的概念[15]。將與巖石長度、含水體積以及水礦化度都相同的條件下的全含水直毛管定義為“標準毛管”，導電效率定義為Pt與Ps之比：

式中，E為巖石的導電效率；Pt和Ps分別為在相同電勢差下，巖石消耗的平均功率和“標準毛管”消耗的功率。

從導電效率的定義上可以得出：（1）巖石的導電效率反映的是巖石的綜合導電能力，一般來說巖石的導電能力受孔隙結構、孔隙的連通性、孔喉尺寸、含油氣性、泥質含量及導電礦物等多種因素的影響，而導電效率可以綜合反映這些因素的影響。（2）“標準毛管”是相同長度、相同含水體積以及相同水礦化度條件下，導電性最高的情況，即消耗功率最大的情況，當巖石中不含地層水以外的導電組分時（如黏土和導電礦物），其導電效率應滿足0≤E≤1。

根據高楚橋等人的推導[12]，對于僅地層水導電，且均勻各向同性的巖石，由導電效率的定義，可得出其測井計算式：

其中，Rw為地層水電阻率；Rt為地層深電阻率；φ為孔隙度；φw為含水孔隙度；Sw為含水飽和度。

測井計算式中，孔隙度φ在地層中主要受裂縫寬度、裂縫傾角、孔洞大小等影響，地層深電阻率Rt由巖石巖性及基巖孔隙度等控制，因此在研究裂縫型儲層巖石導電效率時，主要針對這幾種因素進行研究。

3.巖石導電效率數值模擬

高楚橋等對如圖1（a）所示巖石模型的導電效率進行研究分析，推導并討論了巖石導電效率與孔洞大小、裂縫寬度等之間的關系，并利用巖石導電效率識別碳酸鹽巖儲層類型[16]。在此基礎上，增加了裂縫傾角與基巖孔隙度的變化，如圖1（b）所示。

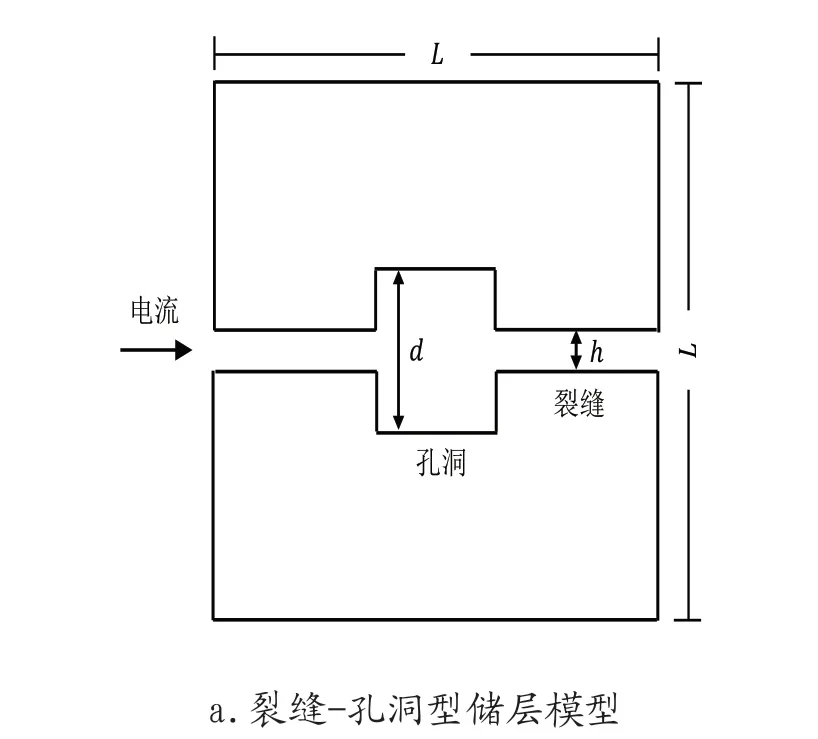
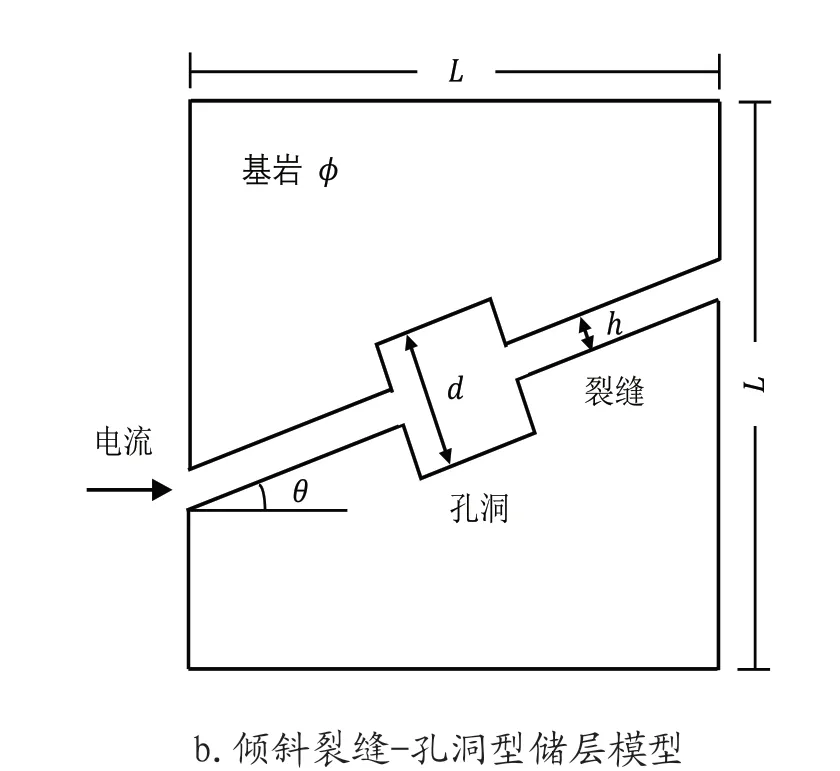
圖1 巖石地質模型

在傾斜裂縫-孔洞型儲層模型中，巖石的長、寬、高均為L，基巖孔隙度為φ，一條寬度為h的裂縫以傾斜角θ貫穿巖石，在裂縫上有一邊長為d的正方體孔洞，孔洞與裂縫中充滿電阻率為Rw的地層水。最終，電流從水平方向進入巖石。

在數值模擬中，根據地質模型建立相應的物理模型并根據導電效率的定義式建立對應的等體積標準毛管模型如圖2所示。在數值模擬軟件中，利用電流物理場，分別在兩個模型的兩端設置相等大小的電勢差，計算得到穩態時巖石和標準毛管所消耗的功率的比值，即導電效率。

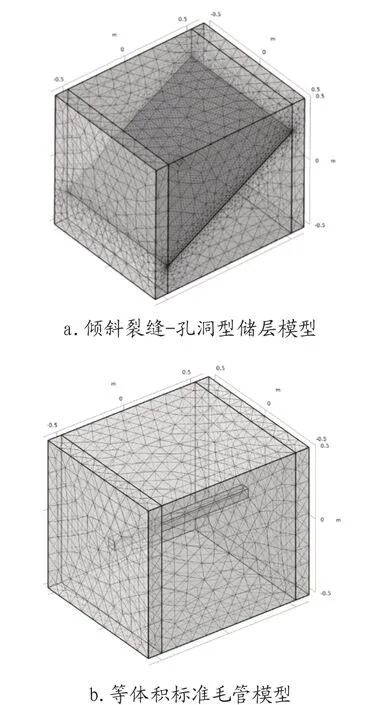
圖2 巖石物理模型

由于影響巖石導電效率的因素眾多，且各因素之間又會相互作用，如果一次數值模擬計算同時考慮多種因素，則不能分析出某一因素對導電效率的影響。因此，數值模擬時采用控制單一變量來逐一分析的方法。主要針對裂縫寬度、裂縫傾角、基巖孔隙度和孔洞大小對導電效率的影響進行分析，各因素的取值范圍如表1所示。

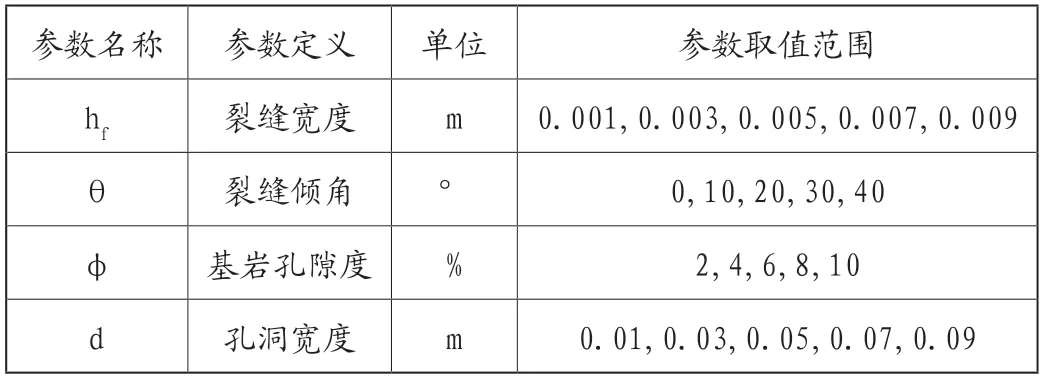
表1 參數定義及取值范圍

4.巖石導電效率影響因素分析

(1)裂縫寬度與巖石導電效率的關系

令裂縫傾角θ分別為0°、20°、40°，基巖孔隙度φ=0.04，孔洞大小d=0.09m，得出巖石導電效率與裂縫寬度hf的關系圖（圖3）。可見巖石導電效率隨裂縫寬度的增大而逐漸增大，且變化的幅度逐漸減小；而隨著裂縫傾角的增大，巖石導電效率隨裂縫寬度的變化趨勢越來越平緩。由于裂縫充滿低電阻率的地層水，裂縫寬度的增大使得巖石整體的電阻率變小，因而巖石耗散的功率增大，導電效率變高。而隨著裂縫傾角的增大，裂縫有效寬度的增加量變小，因此巖石導電效率隨裂縫寬度增加而增加的趨勢也變緩。

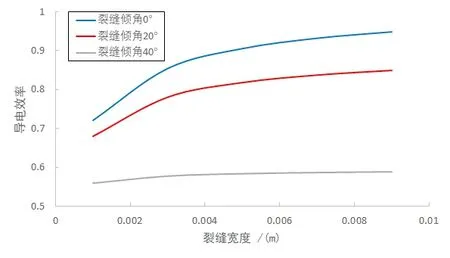
圖3 不同裂縫傾角下裂縫寬度與巖石導電效率的關系

當考慮不同孔洞大小時，巖石導電效率與裂縫寬度的關系如圖4所示。裂縫傾角θ=20°，基巖孔隙度φ=0.04。可見隨著孔洞大小的增大，巖石導電效率的變化趨勢隨裂縫寬度的增大越來越急劇。孔洞大小與裂縫寬度的比值可以表明裂縫整體的不規則程度，寬度越大，裂縫整體越規則，導電效率越高；孔洞大小與裂縫寬度的比值越大，裂縫越不規則，裂縫寬度的增大對導電效率的影響越明顯。

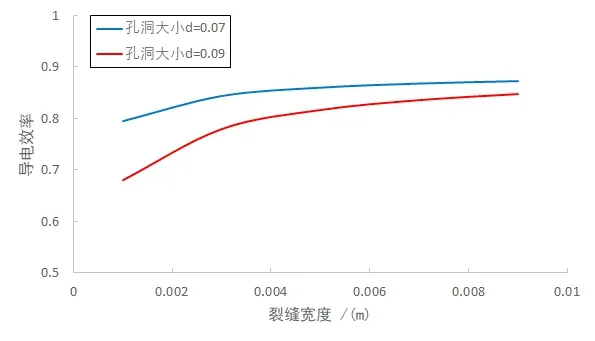
圖4 不同孔洞大小下裂縫寬度與巖石導電效率的關系

(2)裂縫傾角與巖石導電效率的關系

令裂縫寬度hf=0.005m，基巖孔隙度φ=0.04，孔洞大小d=0.09m，得出巖石導電效率與裂縫傾角θ的關系圖（圖5）。可見：由于裂縫傾角的增大，裂縫的有效寬度迅速減小，巖石導電效率也隨之減小。

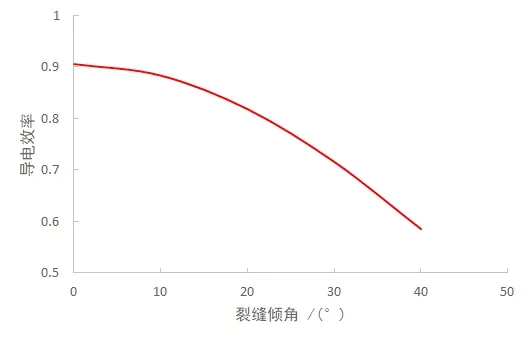
圖5 裂縫傾角與巖石導電效率的關系

(3)孔洞大小與巖石導電效率的關系

令裂縫寬度hf=0.005m，裂縫傾角θ=20°，基巖孔隙度φ=0.04，得出巖石導電效率與孔洞大小d的關系圖（圖6）。可見巖石導電效率隨孔洞的增大而減小，孔洞越大，裂縫整體越不規則，導電效率越低。

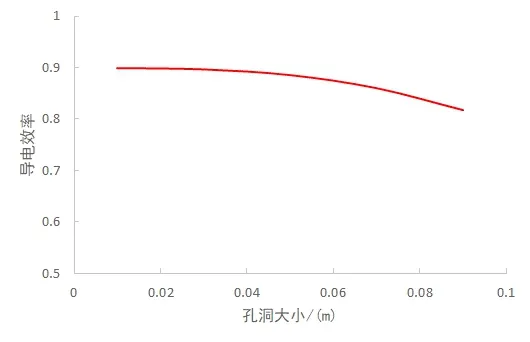
圖6 孔洞大小與巖石導電效率的關系

(4)基巖孔隙度與巖石導電效率的關系

令裂縫寬度hf=0.005m，裂縫傾角θ=20°，孔洞大小d=0.09m，得出巖石導電效率與基巖孔隙度φ的關系圖（圖7）。可見巖石導電效率隨基巖孔隙度的增大而緩慢增大。由于基巖孔隙度的增大導致基巖電阻率降低，使得巖石整體的電阻率降低，在相同電勢差下，巖石整體消耗的功率增大，導電效率升高。但基巖孔隙度對基巖電阻率的影響較小，因而導電效率升高的幅度也較小。

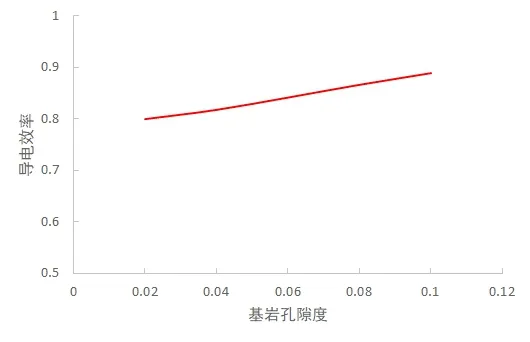
圖7 基巖孔隙度與巖石導電效率的關系

5.結論

基于裂縫型儲層地質特征，建立對應的簡化物理模型，并利用數值模擬的方法研究裂縫-孔洞型儲層導電效率的影響因素，逐一分析了裂縫寬度、裂縫傾角、孔洞大小和基巖孔隙度對導電效率的影響，具體結論如下：

（1）巖石導電效率隨裂縫寬度的增大而逐漸增大，且變化的幅度逐漸減小；而隨著裂縫傾角的增大，裂縫有效寬度的增加量變小，巖石導電效率隨裂縫寬度的變化趨勢越來越平緩；隨著孔洞大小的增大，裂縫整體越不規則，巖石導電效率的變化趨勢隨裂縫寬度的增大越來越急劇。

（2）隨裂縫傾角的增大，巖石導電效率快速減小，對巖石導電效率產生影響的有效裂縫寬度也逐漸變小。

（3）巖石導電效率隨孔洞的增大而減小，孔洞越大，裂縫整體越不規則，導電效率越低；對于越不規則的裂縫，裂縫寬度的增大對導電效率的影響越明顯。

（4）巖石導電效率隨基巖孔隙度的增大而緩慢增大，但基巖孔隙度對基巖電阻率的影響較小，因而導電效率升高的幅度也較小。