Arrhenius 公式和環境作用動力學對壓縮橡膠的精度比較

封先河，魏小琴，楊萬均，何建新，李迪凡

（西南技術工程研究所，重慶 400039）

橡膠制成的O 形密封圈常作為密封材料，廣泛應用于油、氣、水等管道的密封和武器裝備。特別是火箭發動機的密封，長期工作或者倉庫貯存時，由于受機械應力、介質及空氣中氧和溫度的作用，O 形密封圈產生累積永久變形，導致其壓縮比減小而引起泄漏，喪失密封性能，進而導致整個密封系統的功能喪失或報廢，故需對其老化壽命進行預測[1-13]。準確預測其老化壽命的前提是對O 形密封圈老化規律的精準描述。

現行的老化壽命評估方法基本上是采用阿倫尼烏茲公式及其修正公式，并且建立了一系列標準[14-16]。比如GJΒ 92.1 和GJΒ 92.2，以及GΒ/T 27800—2011《靜密封橡膠制品使用壽命的快速預測方法》、GΒ/T 3512—2014《硫化橡膠或熱塑性橡膠熱空氣加速老化和耐熱試驗》。在對這些標準和阿倫尼烏茲公式的實際使用過程中，有時會存在著較大的預估誤差。

環境作用動力學作為一種新的理論[17-21]，正在逐步得到廣泛的應用。本文通過氟硅橡膠高溫加速試驗獲取的試驗數據，分別采用環境作用動力學通解和阿倫尼烏茲公式建立了氟硅橡膠壓縮永久變形率模型，通過3.5 a 的自然環境試驗數據與其進行對比研究。

1 原理

1.1 阿倫尼烏茲公式

早在19 世紀，人們就已經知道溫度對反應速率影響的定性規律。荷蘭化學家Van't Hoff 指出，在室溫附近，溫度升高10 ℃，反應速率增至原來的2～4倍。這條經驗規律稱為Van't Hoff 規則。

1889 年，瑞典化學家Arrhenius（阿侖尼烏斯）在研究蔗糖水解速率與溫度關系時，提出了如下經驗公式：

式中：R為熱力學常數；k為反應速率；A為指前因子或頻率因子；Ea為Arrhenius 活化能。A和Ea是Arrhenius 方程中2 個重要參數。

1.2 環境作用動力學

環境作用動力學建立于21 世紀初，是一個新興的理論。經過10 多年的發展，理論更加成熟，應用逐漸增多，涉及彈簧、橡膠、塑料、彈鏈、膠粘劑、吸波結構等材料及零部件。環境作用動力學由活化粒子、活化粒子濃度、變化進程、變化度量值、環境作用、特征能量值、環境適應性、環境響應性、變化重復性等8 個主要定義和2 個主要假設組成[20]，由假設2 構建了環境作用動力學方程：

式中：I(t,T)為變化度量值；j為比例系數，同時平衡量綱；S(t)為環境適應性；U(T)為環境響應性；Q(t,T)為變化重復性；σ為環境作用。

2 氟硅橡膠壓縮永久變形模型建立

2.1 壓縮永久變形溫度加速試驗

試驗條件基本情況如下：

1）試驗對象：火箭發動機的氟硅橡膠O 形圈。

2）試樣狀態：試樣無孔隙、裂紋、雜質、氣泡、毛邊和機械損傷，表面應當光滑、清潔。試樣處于受壓狀態，在特制夾具中進行，壓縮率為23%。

3）試驗溫度：選取了100、125、150、175、200 ℃等5 個溫度點作為熱空氣加速老化溫度，每個溫度點以3 個試件做平行試驗。

4）試驗設備：熱老化設備為CS101 型電熱鼓風干燥箱。

5）性能指標：壓縮永久變形率ε。

6）試驗標準：參照GΒ/T 7759—1996《硫化橡膠、熱塑性橡膠 常溫、高溫和低溫下壓縮永久變形測定》檢測壓縮永久變形率；參照HG/T 3087—2001《靜密封橡膠零件貯存期快速測定方法》計算氟硅橡膠O 形圈的貯存老化壽命。

首先校正老化烘箱及溫度計，測量橡膠圈的原始高度h0，并將O 形橡膠圈按確定的壓縮比（23%）安放在夾具內，投入高溫老化箱內，按一定周期取出，在標準溫、濕度環境下恢復2 h，測量老化后高度h2，按照式（2）計算壓縮永久變形率ε：

式中：h1為夾具限制器高度；h2為老化后高度；h0為橡膠圈的原始高度。試驗結果見表1。

2.2 基于阿倫尼烏茲公式的氟硅橡膠壓縮永久變形模型

按照阿倫尼烏茲公式（1），于是有：

兩邊同時除以h0，有：

其中：h1/h0=0.758。應用氟硅橡膠壓縮永久變形溫度加速試驗數據，有：A=0.972 45，K25=0.000 214，α=0.74。于是得到25 ℃基于阿倫尼烏茲公式的氟硅橡膠壓縮永久變形模型為：

2.3 基于環境作用動力學的氟硅橡膠壓縮永久變形模型

氟硅橡膠O 形圈的變化度量值I定義為：I=h2/h0。其中，h1為夾具限制器高度；h2為老化后高度；h0為橡膠圈的原始高度。

壓縮作用為壓縮變形量h1/h0減去老化度量值I，隨著自由長度的變化，壓縮作用σ也是變化的。即：

應用環境作用動力學方程可以得到壓縮橡膠的永久變形[22]為：

應用氟硅橡膠壓縮永久變形溫度加速試驗數據，構建誤差函數Y：

式中：Ii為加速試驗數據，Ii(ti,Ti)為計算數據；n為加速試驗數據個數；i=1-n。采用全局最優化計算方法，使得函數Y最小，于是有：E0=-15 172，f=-0.136，g=97.046。

代入式（10）得基于環境作用動力學的氟硅橡膠壓縮永久變形模型：

3 阿倫尼烏茲公式模型和環境作用動力學模型對比研究

3.1 自然環境試驗

氟硅橡膠壓縮永久變形試驗采用溫度加速試驗相同的樣品、工裝、測試方法，試驗地點在海南萬寧試驗站庫房，年平均溫度為27.6 ℃。

3.2 阿倫尼烏茲公式模型和環境作用動力學模型對比

將阿倫尼烏茲公式模型、環境作用動力學模型和試驗結果進行對比（以海南萬寧試驗站庫房年平均溫度為準），如圖1 所示。圖1 中，圓點表示海南萬寧試驗站庫房實際的試驗數據，環境作用動力學的模型靠近實際的試驗數據，阿倫尼烏茲公式模型偏差較大。數值誤差比較見表2。

圖1 阿倫尼烏茲公式模型和環境作用動力學模型對比 Fig.1 Comparison between Arrhenius formula model and environmental action dynamics model

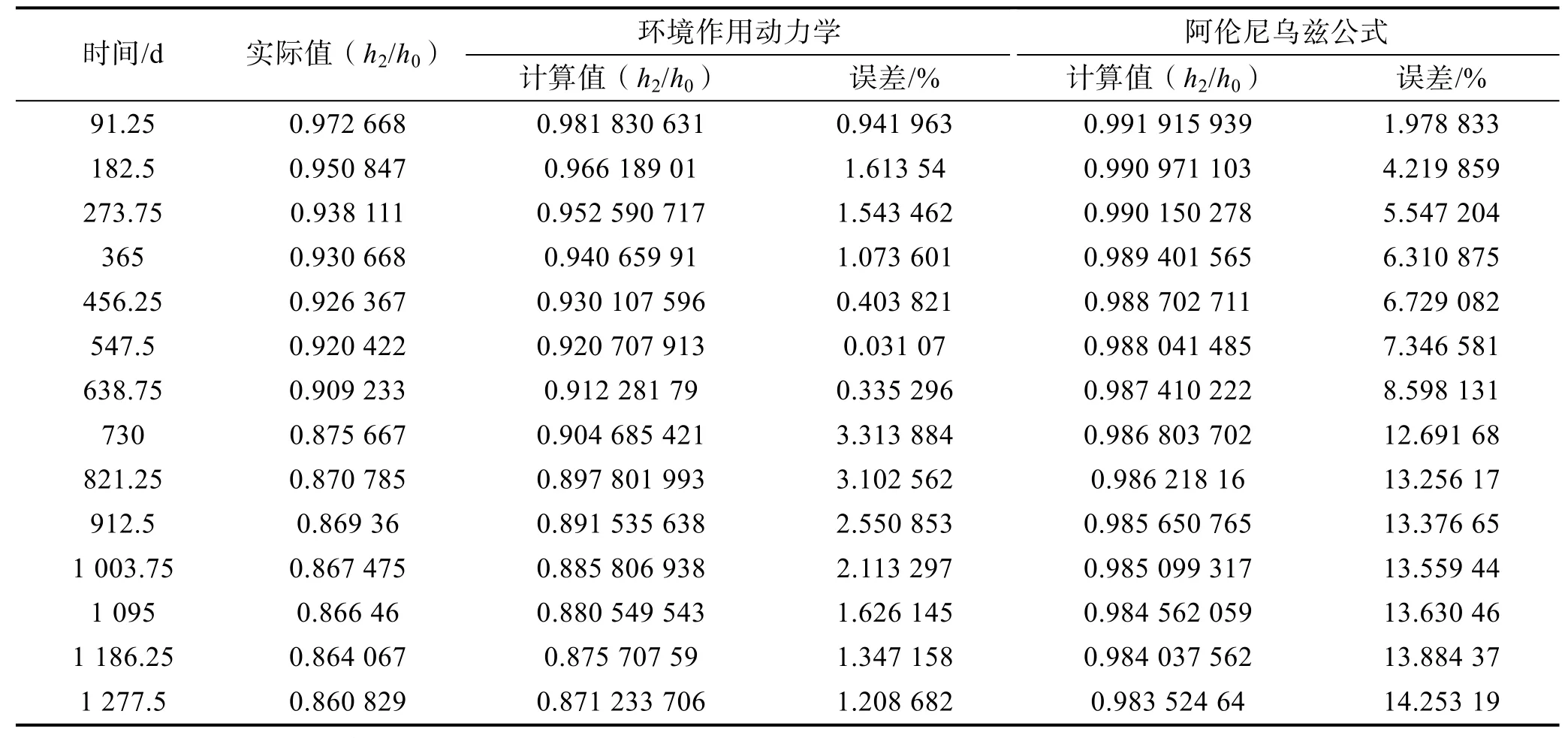
表2 誤差比較 Tab.2 Error comparison

3.3 結果分析

阿倫尼烏茲公式由于不能引入環境作用的概念，將壓縮量固定為夾具限制器高度h1，與實際情況不符，因而造成較大誤差。同時，固定的活化能也是阿倫尼烏茲公式一個誤差來源。

壓縮氟硅橡膠在開始時（時間t=0），氟硅橡膠的原始長度為h0，受到的壓縮量是h0-h1。經過一段時間后，在t=t1時刻氟硅橡膠的長度變為h2，受到的壓縮量是h2-h1。直到t=∞，氟硅橡膠的長度變為h1，受到的壓縮量是為0。

環境作用動力學模型，以壓縮作用σ考慮了壓縮氟硅橡膠壓縮量的變化，從而更加準確地描述了壓縮氟硅橡膠的變化規律。同時，用E0+fT2+gT表示的活化能更加精準。

4 結論

由于阿倫尼烏茲公式沒有考慮環境作用的影響，或者說只考慮了固定環境作用的影響，因此阿倫尼烏茲公式只適用于沒有環境作用或固定環境作用下的物質特征變化。環境作用動力學方程中，有明確的環境作用項σ，適用于復雜環境作用下的物質特征變化規律描述。壓縮氟硅橡膠存在變化的壓縮作用σ，應用環境作用動力學更加合理。實際結果證明，阿倫尼烏茲公式模型與自然環境試驗數據最大誤差為14.25%，環境作用動力學模型與自然環境試驗數據最大誤差為3.32%。