振打機構擺臂疲勞壽命仿真及可靠性分析

張博，趙剛，李元奎

（核工業理化工程研究院，天津 300180）

振打機構擺臂作為反應器的重要組成部分，主要作用于反應過程中粘附在工裝上的物料，通過擺臂傳動電機制造的彈力于器件上，實現物料的高效收集。反應器處于封閉的箱式內，檢維修操作難以進行，振打機構擺臂作為主要傳動與受力部件，直接關系到設備的穩定運行，對擺臂進行疲勞壽命仿真及可靠性分析十分必要[1-3]。

疲勞壽命分析可以為裝置設計提供可靠性數據，提高裝置運行的穩定性，為裝置設計定型奠定基礎[4-7]。游孟平等[8]對壓縮機曲軸進行了動力學分析，獲得了連桿軸頸載荷譜，結合Pairs 公式，計算得到了剩余壽命。王啟瑞[9]對潤滑桿關節軸承進行了仿真分析和實驗驗證，基于桿端體S-N曲線，計算了軸承疲勞壽命，仿真方法與實驗結果相匹配，并滿足設計要求。彭李想[10]基于S-N曲線分析計算了軌道車輛轉向架構架焊縫上的應力集中和焊縫的疲勞損傷，根據疲勞壽命改善技術有效提高了其抗疲勞能力。余建星等[11]基于S-N曲線對浮力風力機張力腿進行了疲勞壽命評估，結果表明，張力筋腱的壽命隨預張力的增大而減小，并以5 MW Sea stars 式風力機平臺為例，驗證了該方法的可行性。本文在疲勞壽命仿真的基礎上，對關鍵影響參數進行影響程度分析，并進行可靠性分析，聚焦薄弱點提出改善建議。

振打機構屬于運動機構，其受力情況復雜，受彈簧彈性系數、壓縮行程、機構質量等影響，因此在進行疲勞仿真前，需對運動機構進行動力學仿真，依次獲得振打機構在各時刻下的應力，在此基礎上進行振打機構的疲勞仿真。疲勞壽命是通過S-N曲線法求解而得，通過對振打機構的動力學仿真及應力仿真得到零件的應力大小S，通過查找零件的S-N曲線，計算其相應的壽命循環數N[11-14]。通過對影響振打機構擺臂疲勞壽命的關鍵參數進行影響程度仿真分析，獲得其壽命分布及其可靠壽命，校核振打機構的可靠性是否滿足要求。其流程如圖1 所示。

圖1 疲勞仿真及可靠性分析流程 Fig.1 Flow chart of fatigue simulation and reliability analysis

1 疲勞壽命仿真方法

1.1 振打機構模型

振打機構如圖2 所示，主要由機架、振打電機組件、撥輪、擺臂、波紋管及彈簧等組成。振打電機的工作原理如下：電機旋轉帶動撥輪旋轉，撥動振打裝置中波紋管的后端板向后運動，從而后部的彈簧儲能，當電機撥輪旋轉到另一端時，波紋管后端板和撥輪脫離接觸，其在彈簧作用線向工件方向快速運動，帶動擺臂也向工件運動，敲擊工件或工裝，形成振打。根據工藝要求，反應器保持在一定溫度下運行，溫度區間為常溫至500 ℃，振打機構保持周期性運行。根據使用期限要求，振打機構擺臂設計壽命為1.44×106次。

1.2 動力學仿真約束及載荷設置

在進行振打機構擺臂的疲勞仿真前，需進行動力學仿真，以獲得疲勞仿真所需的應力輸入。本仿真試驗的動力學約束有鉸鏈約束、棱柱約束、凸輪機構約束、彈簧阻尼器和接觸面約束。

在固定端和撥輪間設置鉸鏈關節，模擬電機與撥輪的約束，并在源端設置轉速以提供動力。在撥輪和波紋管后端面間設置凸輪-從動件1 約束，使得波紋管后端面隨著波紋的轉動而移動。在波紋管后端板的后部與機架間設置彈簧-阻尼器1 約束，設置彈簧彈性系數為4 900 N/m，模擬儲能彈簧作用，并在彈簧-阻尼器1 的設置中設置彈簧作用方式為僅壓縮。在波紋管后端板的前部與機架間設置彈簧-阻尼器2 約束，設置彈簧彈性系數為192.8 N/m，模擬波紋管作用，并在彈簧-阻尼器2 的設置中設置彈簧作用方式為雙向。在擺臂堵頭和工件間設置接觸約束，模擬振打接觸表面。

1.3 疲勞模型設置

添加疲勞物理場，選取并添加應力壽命模型，準則選擇逼近S-N曲線，設置過渡應力、過渡壽命、持久極限、持久壽命如圖3 所示。過渡應力為材料S-N曲線上所選取的應力，一般選取壽命為1 000 次所對應的應力作為過渡應力，過渡應力下的壽命即為材料的過渡壽命。持久應力為材料的對稱循環疲勞持久極限，疲勞持久極限所對應的壽命循環數一般取107。S-N曲線數據根據試驗數據與資料查閱所得[15-17]。

實驗采用Bech-Rafae-lsen躁狂量表對患者進行評分,同時將患者的臨床治療效果分為治愈、顯著進步、好轉、無效幾個層次。BRMS減分率高于75%時,為治愈;當BRMS減分率在50%和74%之間時,為顯著進步;當BRMS減分率在25%和49%之間時,為好轉;當BRMS減分率低于24%時,為無效。臨床治療總有效率包括治愈、顯著進步和好轉。另對患者的不良反應發生情況進行統計。

圖3 S-N 曲線設置 Fig.3 Setting of S-N curve

1.4 參數影響程度及壽命可靠性分析

本仿真試驗使用對數正態分布對產品可靠性進行分析。壽命可靠性分析的前提是獲得各壽命影響參數發生微小變異后的壽命改變量，從而計算其系數ti。因此，需選取對疲勞壽命有較大影響的參數作為研究對象。對疲勞壽命有影響的參數主要為性能參數，性能參數的變異系數取0.05，影響參數均視為正態分布[18]。壽命影響參數的標準差為其變異系數與均值的乘積，取0.1 倍的參數標準差作為該參數的變異值[19-20]。

系數ti=ΔTi/Δxi，其中ΔTi為參數變異后壽命改變量，Δxi=0.1σxi，為變異值。通過研究分析，振打機構擺臂的主要參數有抗拉強度、彈性模量E、表面加工系數，均為性能參數。各參數均值、標準差及其變異值見表1。

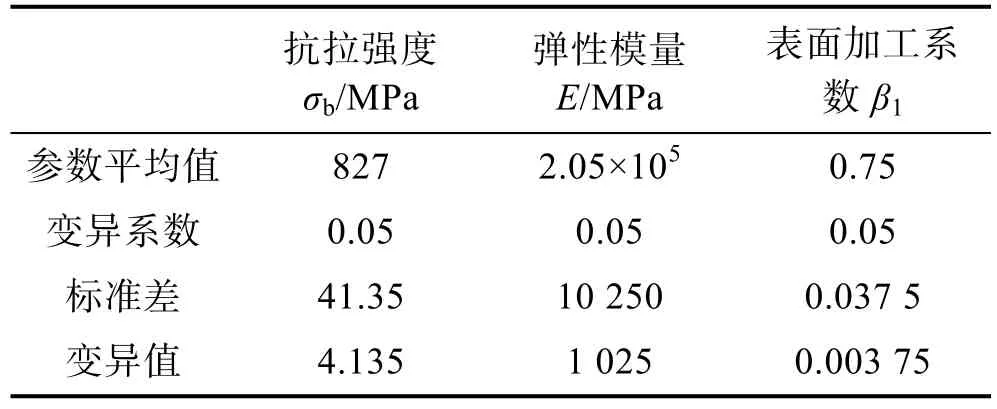
表1 振打機構擺臂疲勞壽命影響參數 Tab.1 Effect parameters on fatigue life of swing arm of rapping mechanism

2 仿真結果與討論

2.1 動力學仿真結果

振打機構擺臂各時間點下的位移如圖4a—d 所示。擺臂從壓縮極限位置到沖擊工件再到回彈整個過程的速度隨時間的變化曲線如圖4e 所示，位移隨時間的變化曲線如圖4f 所示。由圖4 可知，振打機構擺臂振打進給時間約為0.28 s，沖擊速度約為3 m/s，回彈速度約為2.7 m/s。

圖4 振打機構擺臂位移及擺臂運動速度、位移隨時間的變化曲線 Fig.4 Displacement of swing arm of rapping mechanism and movement speed and displacement of swing arm over time: a) initial position;b) compression limit position;c) impact workpiece position;d) position after rebound;e) movement speed of swing arm;f) movement displacement of swing arm

振打機構各時間點下的應力云圖如圖5 所示。由圖5 可知，振打機構擺臂運動過程中的最大工作應力為559 MPa，位于擺臂前端部與擺臂堵頭連接位置。這是由于該處與振打作用位置十分接近，且桿體為空心桿，其截面在此處急劇減小，引起應力集中。

圖5 擺臂初始位置、極限位置、接觸面及回彈位置應力云圖 Fig.5 Stress pattern of swing arm at (a) initial position,(b) limit position,(c) contact surface and (d) rebound position

2.2 振打機構疲勞仿真結果

疲勞仿真結果如圖6 所示。常溫下擺臂的最低壽命為9.55×105次載荷循環，500 ℃環境溫度下擺臂的最低壽命為1.58×106次載荷循環，大于常溫下的疲勞壽命。這是由于高溫環境下材料彈性模量變小，材料更易發生變形，從而增強了材料的抗沖擊能力。由于擺臂并非時時處在500 ℃高溫環境，采用保守計算方法，取常溫下擺臂的疲勞壽命作為擺臂的疲勞壽命估計值。

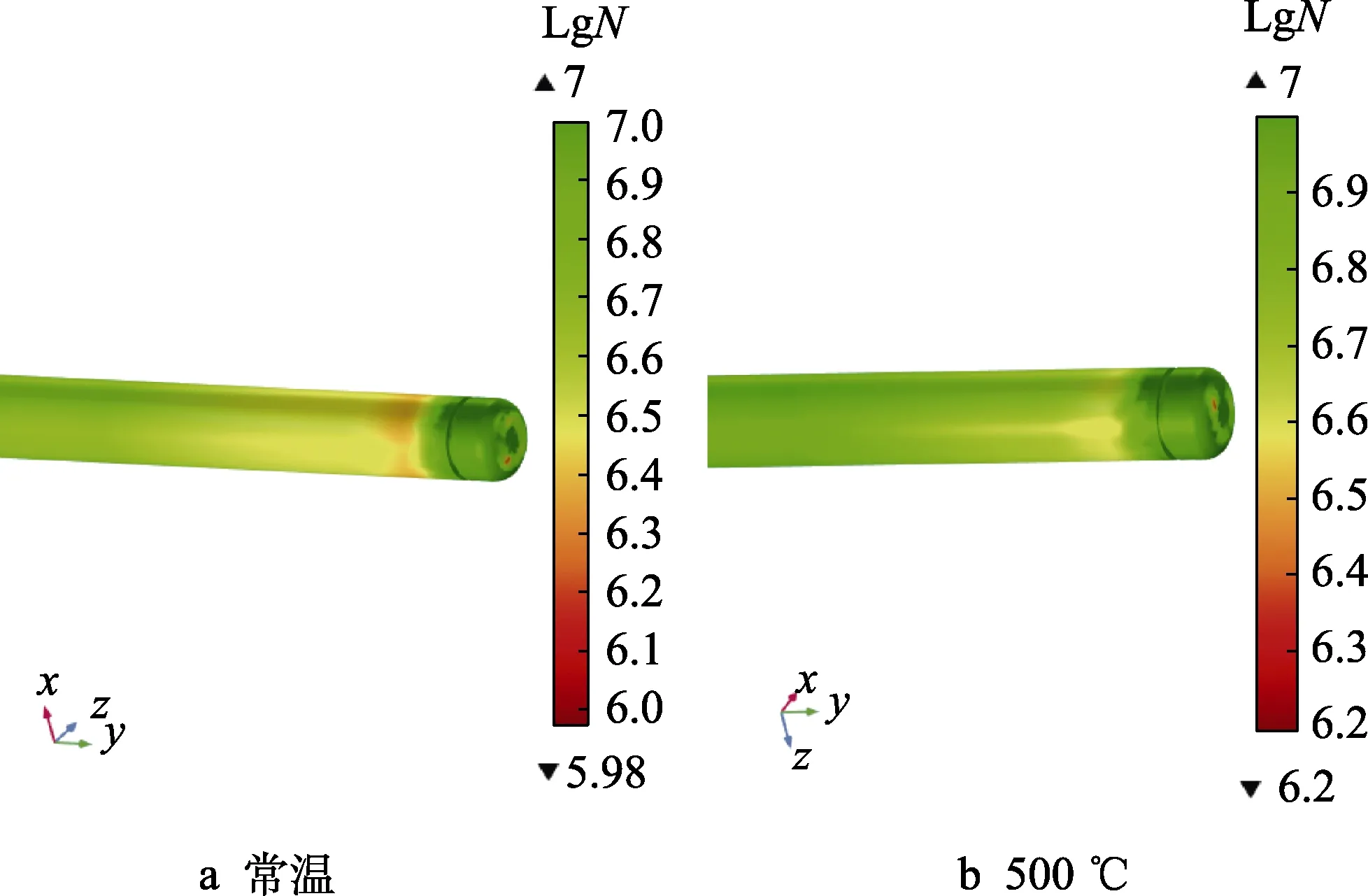
圖6 常溫及500 ℃下擺臂的疲勞壽命云圖 Fig.6 Fatigue life pattern of swing arm at normal temperature (a) and 500 ℃ (b)

在對擺臂疲勞分析時，當選取最大應力為482 MPa 時，疲勞壽命增加到1.95×106，滿足1.44×106次工作循環的設計要求。若要使得擺臂內部應力由559 MPa 降低到482 MPa，壁厚應由原來的1.5 mm增大到1.77 mm。當管壁壁厚選取為3 mm 時，擺臂內部應力降為280 MPa，經仿真計算，擺臂為無限壽命件。

2.3 參數影響程度仿真分析結果

依次對振打機構的各壽命影響參數添加表1 中的變異值，得到擺臂的疲勞壽命云圖如圖7 所示。圖7 a 為抗拉強度σb正負變異后壽命云圖，當抗拉強度參數分別進行正負0.1 的變異后，擺臂壽命分別為976 787.3、926 616.4 次。圖7b 為表面加工系數β1正負變異后的壽命云圖，當表面加工系數分別進行正負0.1 的變異后，擺臂壽命分別為975 438.7、927 897.5次。圖7c 為彈性模量E正負變異后的壽命云圖，當彈性模量參數分別進行正負0.1 的變異后，擺臂壽命分別為344 270.7 次及1459 486 次。由此可見，彈性模量的變異對擺臂壽命的影響最大。

圖7 擺臂壽命影響參數抗拉強度、表面加工系數和彈性模量影響程度仿真結果 Fig.7 Simulation results of effect parameters of swing arm life in terms of tensile strength (a),surface processing coefficient (b) and effect degree of elastic modulus (c)

變異值分別取正、負所得的壽命影響參數系數ti的計算結果分別見表2 與表3。其中，ti-1為變異值取正的系數計算結果，ti-2為變異值取負的系數計算結果。可靠性參數的計算結果見表4。

表2 擺臂壽命影響參數系數計算結果（變異值取正）Tab.2 Calculation results of parameter coefficients affecting swing arm life (the variation value is positive)

表3 擺臂壽命影響參數系數計算結果（變異值取負）Tab.3 Calculation results of parameter coefficients affecting swing arm life (the variation value is negative)

表4 擺臂可靠性參數計算結果 Tab.4 Calculation results of reliability parameters of swing arm

2.4 可靠性分析

本文對壁厚為1.5 mm 的擺臂進行可靠性分析，具體過程如下。

式中：μT為壽命均值；σT為壽命標準差。解得常數t0=1.027×108，標準差σT=5.587×106。當參數取中間值時，仿真所計算的壽命為產品的平均壽命，即μT=9.515×105次循環。因此，μT、σT可用式（3）和式（4）表示：

令μT=1.44×106，保持σb、β1不變，解得E=2.041× 105MPa；保持E、β1不變，解得σb=907.76 MPa；保持σb、E不變，解得β1=0.827 3。

將μT、σT的值代入式（5）和式（6）。

計算得μlgT=5.203 4，σlgT=0.880 3。

將μlgT、σlgT的值代入式可靠度方程，得到擺臂的可靠度函數，如式（7）所示。

繪制擺臂可靠度與疲勞壽命（R-T）關系曲線，如圖8 所示。

從圖8 中可知，當壽命次數T=1 440 000 時，可靠度R值為0.138 78；當R=0.8 時，其壽命值約為29 005 次；當R=0.9 時，其壽命值約為11 891 次。

圖8 擺臂可靠度壽命曲線 Fig.8 Reliability life curve of swing arm

2.5 實驗驗證

采用2 mm 壁厚的擺臂進行振打實驗驗證，振打次數超過1.5×106，擺臂仍可正常運行，這與仿真結果相符合。

3 結論

通過對振打機構進行疲勞仿真及壽命分析，獲得以下結論：

1）當擺臂壁厚取值＞1.77 mm 時，擺臂的平均壽命大于144 萬次，滿足產品設計要求。

2）振打機構擺臂應力最大的位置位于擺臂與前部堵頭連接的位置，這是由于該處存在截面突變，且靠近振打工作點，引起應力集中。

3）疲勞壽命與彈性模量E負相關，與抗拉強度σb和表面加工系數β1正相關。

4）對于壁厚度為1.5 mm 的擺臂，可靠度R取0.8 時，擺臂的可靠壽命約為29 005 次；可靠度R取0.9 時，擺臂的可靠壽命約為11 891 次。

根據仿真分析結果，對振打機構擺臂提出以下改進建議：

1）在不降低材質抗拉強度σb及表面質量系數β1的前提下，選取彈性模量E小于2.041×105MPa 的材質作為擺臂材質。

2）在不提高材質彈性模量E及不降低表面質量系數β1的前提下，選取抗拉強度σb大于907.76 MPa的材質作為擺臂材質。

3）提高擺臂及堵頭的表面質量，改為精車表面（β1=0.9），使表面質量系數β1大于0.827 3，從而提高疲勞壽命。

4）使擺臂的壁厚不小于1.77 mm，減小擺臂所承受的應力。

5）改進擺臂截面設計，使得堵頭與擺臂連接處的截面緩慢變化，減少應力集中。

本文基于S-N曲線，針對振打機構擺臂開展疲勞壽命仿真及關鍵參數影響程度仿真分析，獲得結構、材質、加工系數等參數與壽命的關系，為擺臂的設計定型及制造加工提供數據支撐。本文為具有震動、彈性等功能的機械加工件的仿真分析提供方法與思路，針對關鍵參數進行疲勞壽命仿真分析，提出設計及加工建議，保證產品的壽命達到要求。