中考復習:從“數與式”出發
文/江海人

一、知識塊解析
實數的相關概念,包括相反數、絕對值、科學記數法、實數的大小比較等;平方根、算術平方根和立方根及相關運算;實數的混合運算也是高頻考點,比如絕對值化簡、零次冪、平方、立方、負數次冪、開平方、開立方等。
整式的考點主要是代數式的求值,整式化簡后代入求值,整式的運算(包括冪的運算性質、合并同類項、乘法公式等),還有因式分解。
二次根式的考點主要涉及二次根式的性質、化簡及運算,二次根式的估值等。
分式的考點主要是分式和最簡分式的概念,分式的基本性質,分式的約分與通分,分式的加、減、乘、除運算,整數指數冪的概念及運算性質。
二、知識結構圖
1.實數知識結構圖
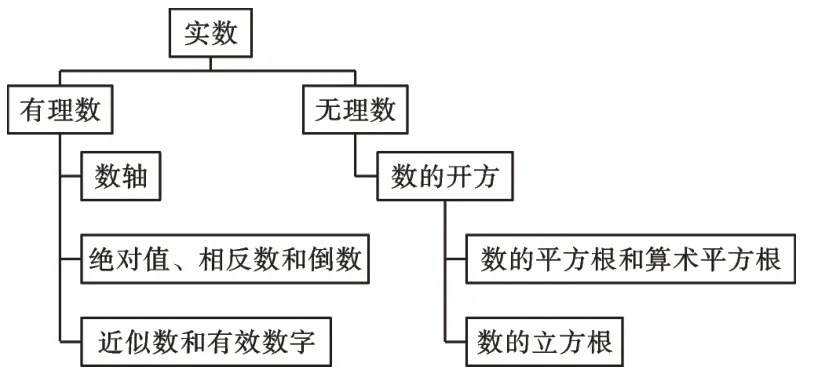
2.整式、分式、二次根式知識結構圖
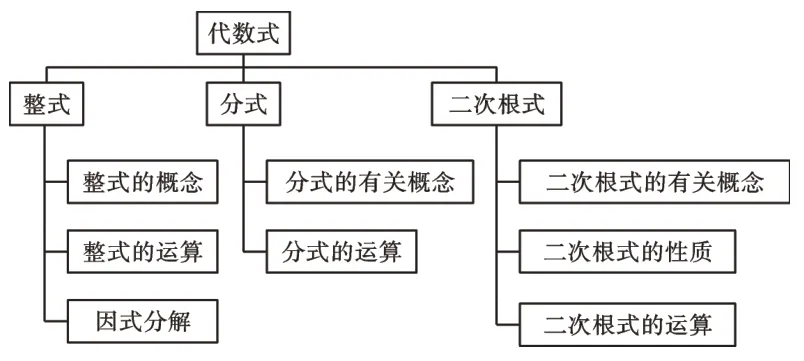
三、易混點辨析
實數的易混點主要為:對平方根、算術平方根、立方根的概念與性質理解不透。比如,求一個正數的平方根時漏掉一個,而求立方根時又多寫了一個;又如,對一個實數歸類時只看表面形式,應該化簡后再判斷;再如,實數混合運算中的“序”也可能出現錯誤。
整式知識塊的易混點也較多。其一,合并同類項與同底數冪的運算要注意辨析;其二,冪的乘方、積的乘方與同底數冪的乘法的不同;其三,整式乘法與因式分解的差別;其四,幾個乘法公式之間不能混用。
分式的易混點主要是分式的運算。比如,分式的乘除運算,對于形式上比較繁雜的分式,在約分時容易出錯;對于分式的加減運算,主要是在進行異分母分式加減運算時,通常要經歷找公分母、通分、加減、化簡這4個步驟,由于步驟多、運算量大、綜合性強,很容易出錯。復習時,我們首先要找準公分母。
要注意辨析二次根式的運算對被開方數(式)的取值范圍的限制。一般來說,要“先觀察,后計算”“先化為最簡二次根式,后計算”“利用乘法公式進行計算”等。值得注意的是,雖然教材以“理解二次根式的性質和運算,并會熟練運用法則進行運算”為重點,突出二次根式的性質和法則的數學本質,而對分母有理化、同類二次根式等概念采取淡化處理,只結合具體例子進行說明,但這并不意味著可以弱化分母有理化。同時要注意,“根號下僅限于數的二次根式的四則運算”的限制是最低要求,復習時要適當訓練含有字母的二次根式的化簡、四則運算,因為這類二次根式的化簡運算不一定會直接考查,有時可能會出現在一些綜合題的解題過程中。

