基于覓食能力分配搜索任務的侏儒貓鼬優化算法

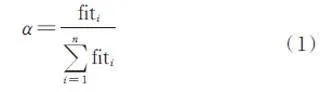
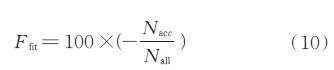
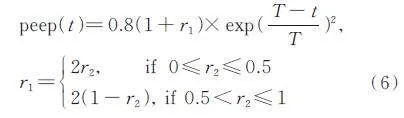
摘 要：針對侏儒貓鼬優化算法存在的不足，提出一種基于覓食能力分配搜索任務的侏儒貓鼬優化算法。首先采用tent 混沌自適應步長平衡全局搜索與局部開發；針對al?pha 組搜索盲目性問題，優化其移動方向及移動能力；針對偵察組算法移動方向存在誤導性問題，增強其個體糾錯能力，從而提升個體覓食能力；改進保姆組移動算法，提升種群的局部開發能力；最后提出一種新的種群覓食策略，平衡各算法之間調用策略，提升算法整體性能。通過解決12 個基準測試函數與支持向量機的參數優化問題，對該文算法性能進行數值實驗驗證。實驗結果表明FADMO 的全局收斂精度與全局收斂速度均有明顯提高，并適用于實際問題求解。

關鍵詞：智能優化；侏儒貓鼬優化算法（DMO）；覓食能力分配任務；支持向量機參數優化

中圖分類號： TP391 文獻標識碼： A 文章編號： 1673-8462（2023）03-0074-12

0 引言

由于群智能優化算法在科學、工程等諸多領域（如圖像處理［1-2］、路徑規劃［3-4］、參數優化［5-6］等）已經得到了較好的應用，因而群智能優化算法的研究越來越受到國內外研究者的重視。目前針對群智能優化算法的研究主要有：一種是原創性地提出群智能優化算法（如海鷗優化算法（SOA）［7］、麻雀搜索算法（SSA）［8］、學生心理優化算法（SPBO）［9］、黑寡婦優化算法（BWO）［10］、算術優化算法（AOA）［11］、阿奎拉優化算法（AO）［12］等）；另一種是進一步完善現有群智能優化算法［13-15］，并將其應用于解決工程等方面的實際問題。

侏儒貓鼬優化算法（Dwarf Mongoose Optimiza?tion，DMO）［16］是Agushaka 等人受侏儒貓鼬群體內部社會分工及各分工下協同覓食行為的啟發，于2022 年提出的一種新的群智能優化算法。然而DMO 存在全局收斂速度慢、優化精度不高、易陷入局部最優等問題。針對DMO 存在之不足，國內外研究者提出了各種改進方法：Elaziz 等人［17］通過引入量子進化算法改進局部搜索，以期避免陷入局部最優陷阱；Olatunji 等人［18］通過引入模擬退火算法改進局部搜索，以期提升算法的局部搜索能力；賈鶴鳴等人［19］通過引入透鏡成像反向學習與精英池策略，以期提升算法的收斂性能；Agushaka 等人［20］通過改進種群內各分工算法策略，以期能提升算法的探索和開發能力；趙世杰等人［21］通過引入領導者策略與支配解動態縮減進化策略，以期提升算法的收斂性能與多樣性。盡管文獻［17-21］提出的改進策略在一定程度上改善了DMO的優化性能，但仍存在收斂速度較慢、優化精度不高之不足，仍有待進一步提升。

基于此，筆者提出基于覓食能力分配搜索任務的侏儒貓鼬優化算法（The Dwarf mongoose Optimiza?tion Algorithm based on Foraging Ability to AllocateSearch Tasks， FADMO）：首先通過tent 混沌自適應步長優化個體移動距離，平衡算法全局搜索與局部開發的能力；通過優化alpha 組搜索模型使得其個體移動方向更加明確；通過優化偵查組搜索模型改進偵查組個體定向開發能力；通過優化保姆組搜索模型使得保姆組在局部尋優上具有更強的性能；最后通過構建一種新的種群內個體任務分配方法使得種群內個體根據個體信息在不同搜索模式上變換，從而提升算法整體尋優精度與收斂速度。并通過數值實驗仿真與解決SVM 參數調優問題驗證了本文提出的改進策略是有效的和可行的。

1 DMO 算法簡介

1.1 DMO 算法基本思想

侏儒貓鼬優化算法（DMO）［16］的基本思想如下：

DMO 算法中將侏儒貓鼬種群的社會結構分為al?pha 組、偵查組和保姆組。其中alpha 組與偵查組為同一組個體，即尋找新的睡眠丘與覓食是由同一群貓鼬完成的，當alpha 組進行覓食活動時，若保姆交換條件達成，它們就會變更為偵察組去尋找拜訪新的睡眠丘。

在侏儒貓鼬種群中，alpha 組為模擬種群作為一個整體覓食，其首領由概率α 根據公式（1）計算得出。

其中，fiti 表示個體i 的適應度，alpha 組個體數為n - bs，bs 為保姆組個數。

alpha 組在雌性首領鳴叫的引導下，根據公式（2）尋覓食物源。

xi （ t + 1 ）= xi （ t ）+ phi × peep （2）

其中，phi 為[-1，1 ] 中的均勻隨機數，peep 為雌性首領“發聲”距離（DMO 置peep = 2），t 為當前迭代時刻。且在每次迭代后，根據公式（3）計算alpha 組睡眠丘值，并根據公式（4）計算alpha 組睡眠丘的平均值。

標準DMO 中，保姆組的表現形式為保姆交換條件：當alpha 組內個體覓食活動耗時C 超過DMO 設置的保姆交換條件L 時，則代表該個體覓食效率不佳，激活保姆交換條件，alpha 組中覓食能力較差的個體將會被alpha 組舍去并隨機生成新的位置。完成保姆交換條件判斷后，alpha 組將變為偵察組用于尋覓種群中的下一個睡眠丘。

1.2 DMO 算法實現步驟

基于以上算法思想，DMO 給出的算法模型和實現步驟如下：

開始：輸入目標函數f （ x ），種群規模n，保姆組個數bs，alpha 組個數n = n - bs，保姆交換條件L。

Step1：初始化種群xi，i = 1，…，n。

Step2：設置個體計數器C，并計算每一個體的適應度fiti = f （ xi ），i = 1，…，n。

Step3：選取alpha 組雌性首領。alpha 組中雌性個體i 被選為首領的概率α 按公式（1）計算。

Step4：alpha 組中個體在雌性首領的引導下，按公式（2）尋覓食物。

Step5：計算由Step4 確定的新位置的適應度值fiti （ t + 1 ），若fiti （ t + 1 ） 優于fiti （ t ），則更新個體位置，反之不變。

Step6：根據公式（3）計算新的睡眠丘。

Step7：根據公式（4）計算alpha 組睡眠丘的平均值。

Step8：判斷alpha 組個體是否滿足保姆交換條件，若滿足則重新初始化對應個體，并計算其適應度值。

Step9：alpha 組轉換為偵察組，按公式（5）更新位置，并計算xi （ t + 1 ）的適應度。

Step10：判斷是否達成停止條件：若是則轉Step11；否則轉Step3。

Step11：算法停止，輸出最優位置和相應最優值。

2 本文算法

2.1 tent 混沌自適應步長

標準DMO 中，搜索步長取定值（DMO 置peep =2）限制了個體搜索的靈活機動性，削弱了個體的全局探索和局部開發能力。且現實生活中，隨覓食時間增加，種群成員逐漸聚集，呼喚同伴所需要的“ 發聲”距離也會越短。針對上述特性，本文算法提出tent 混沌自適應步長：

其中，t 為當前迭代次數，T 為最大迭代次數，r2 為[ 0，1 ] 中的隨機數。peep（ t ） 關于時間t 的變化關系如圖1 所示。

分析公式（6）：a）peep（ t ） 呈現混沌下降波動特征，這可增強個體搜索的遍歷性、隨機性和靈活性，從而增強了種群在算法前期的全局探索能力。b）peep（ t ） 的波動范圍隨著搜索時間t 的增加呈現越來越窄趨勢且步長逐漸減小，提升了個體在算法后期的局部搜索能力，進而增強了算法的局部開發能力，也反映了覓食時間越長，發聲距離越短的特征。

2.2 改進Alpha 組搜索模型

標準DMO 中alpha 組搜索模型為公式（2），其目的是讓alpha 組個體不受群體其他個體的影響，而開展球域范圍內的自由活動。但這種搜索策略為無目的盲目移動，造成尋優方向無序，影響算法收斂性能；且該覓食策略使得覓食引領者之間各自為政，僅根據自身位置規劃覓食路徑，降低了種群找到全局最優的效率。現實生活中，若覓食引領者（alpha 組）中的某個成員發現某地方的食物比較多，通常會呼喚同伴前來這一區域覓食。基于上述問題，本文算法針對標準DMO中alpha 組覓食算法（公式（2）），提出改進alpha 組搜索方法如下：

xi （ t + 1 ）= xi （ t ）+ r × peep（ t ）×（（ 0.7 × Gbest （ t ）+0.3 × xj （ t ） ）- xi （ t ） ） （7）

i = 1，…，l s，j = 1，…，ls。其中：r 為[ 0，1 ] 中的均勻隨機數，Gbest （ t ） 為算法當前全局最優位置，xj 為al?pha 組隨機選擇的一個個體。

分析公式（7）：a）公式（7）通過引入當前全局最優位置Gbest （ t ） 與alpha 組隨機個體xj 進行加權組合，使得本文算法alpha 組在保證移動方向偏向當前全局最優位置的同時增加了擾動，避免算法出現早熟和陷入局部最優陷阱的情況。b）通過引用tent 混沌自適應步長peep（ t ） 替代標準DMO 中的固定步長peep 使得覓食引領者的運動距離更具多樣性，提升了算法求解的靈活機動性，增強了個體的覓食能力與跳出局部最優陷阱的能力。

2.3 偵察者搜索模型

標準DMO 中偵查組為alpha 組轉換而來，所用移動公式為公式（5）。其目的是比較alpha 組內所有個體當前時刻與上一時刻適應度值的優劣，進而修正alpha組個體的移動方向，使個體朝向理論最優位置移動。觀察可得：a）φ 由公式（4）生成，為alpha 組所有個體睡眠丘的平均值；b）移動向量M 由公式（7）生成，是決定貓鼬移動到新的睡眠丘的方向向量。但alpha 組中不同個體的位置不同，所需要修正的方向與距離均不相同。因此，公式（5）易造成單一個體進行錯誤的覓食移動，影響算法的收斂性能。基于上述問題，本文算法針對標準DMO 中偵察組覓食算法（公式（5）），提出改進偵查組搜索方法如下：

xi （ t + 1 ）= xi （ t ）+ b × exp （ |smi |）× peep（ t ）×xi （ t ）+ c × peep（ t ）×（ Gbest （ t ）- xi （ t ） ） （8）

其中b = smi /| smi |，smi 由公式（3）確定，c = 0.01，Gbest （ t ）為種群當前最優位置。

分析公式（8）：a）smi 反映了個體i 當前時刻與上一時刻適應度值的優劣。其中：smi lt; 0 表示個體i 當前時刻對應位置更靠近理論最優位置，反之表示個體i當前時刻對應位置更遠離理論最優位置；b）| smi |則表示個體i 當前時刻與上一時刻適應度值變化幅度，| smi |越大表示個體i 當前時刻較上一時刻適應度值變化明顯，應采用大步長進行全局開發，反之表示個體i當前時刻較上一時刻適應度值變化微弱，應采用小步長進行局部尋優。基于上述兩點，公式（8）添加b =smi /| smi |，其值為1 或-1，為偵察組個體前進方向；添加exp （ |smi |） 作為偵察組移動步長權重；添加c ×peep（ t ）×（ Gbest （ t ）- xi （ t ） ），增加個體i 覓食移動的多樣性，避免算法陷入局部最優。

2.4 保姆者搜索模型

標準DMO 中，對滿足保姆交換條件的個體進行隨機位置生成，屬于隨機覓食策略。這種搜索策略因其過于盲目，會造成算法整體收斂速度過慢，收斂精度較低的問題。且保姆組負責照顧侏儒貓鼬幼崽成長，隨機位置生成會導致食物質量不一。現實生活中，為了確保種群中侏儒貓鼬幼崽的成長，在找到更優的覓食區域后種群會將睡眠丘（老巢）安置于此，方便幼崽覓食成長，并由種群中覓食能力較弱者擔任保姆，覓食的同時負責幼崽的安全保衛工作。基于上述問題，本文算法針對標準DMO 中保姆組（滿足保姆交換條件）的隨機覓食策略，提出改進保姆組搜索方法如下：

xi （ t + 1 ）= Gbest （ t ）+ d × r × peep（ t ）× Gbest （ t ） （9）

其中d 取0.7，r 為[-1，1 ] 中的均勻隨機數，Gbest （ t ） 為當前迭代時刻中的種群最優位置。

分析公式（9）：a）本文算法將保姆組個體遷移至種群當前最優位置，其目的為保證具有充足的食物，從而更好的照顧侏儒貓鼬幼崽的成長；b）公式（9）以種群當前最優位置為球心，使個體i 在球域范圍內開展局部搜索。因保姆組需要保護侏儒貓鼬幼崽的安全，其移動能力也會因此受到限制，故公式（9）中添加參數d（本論文取0.7）以模擬行動受限的移動算法。

2.5 個體任務分配方法

本文在標準DMO 基礎上對其三種不同的搜索算法進行了改進。為了有效地應用三種改進搜索算法，本文算法設置不同分組分配策略如下：1）本文算法設置保姆交換參數L = max { 0.02 × T，3 }，其中T 為最大迭代次數，設置計數參數Ci，其中i = 1，2，…，n；2）種群中個體i 初始化時其Ci = 0，在t + 1 時刻個體i 求得新位置適應度值劣于t 時刻適應度值時Ci = Ci + 1，反之Ci = 0；3）當個體i 的Ci lt; ceil（ L/3 ）時，即認為該個體尋優能力較強，設為alpha 組個體，執行移動策略公式（7），當ceil（ L/3 ） ≤ Ci lt; L 時，即認為該個體執行公式（7）策略效果較差，應由領袖變為偵察者，執行移動策略公式（8），當Ci = L 即代表該個體尋優能力最差，身份變更為保姆者，執行策略公式（9），并重置Ci = ceil（ L/3 ）- 1。其中ceil（ x ） 表示對x向上取整。

2.6 算法實現步驟

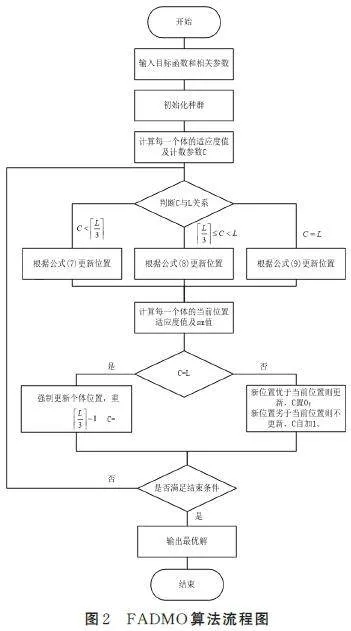
FADMO 算法流程圖見圖2，算法實現步驟如下：

Input： 目標函數f （ x ），種群規模n，搜索空間維數D，保姆交換參數L。

Step1： 初始化種群xi，評估每一個體的適應度值fiti （ t ），選出最優個體位置Gbest （ t ），重置個體Ci，i =1，2，…，n。

Step2： 根據個體任務分配方法判斷個體所屬組別，根據組別條件分別選擇公式（7）、（8）、（9）更新其位置。

Step3： 評估每一個體的適應度值fiti （ t + 1 ），若優于fiti （ t ），則更新個體位置，反之不變。

Step4： 根據新位置適應度評判與個體任務分配方法更新Ci，更新smi。

Step5： 判斷是否達成停止條件：若是則轉Step6；否則轉Step2。

Step6： 算法停止，輸出最優位置和相應最優值。

2.7 算法復雜度分析

設種群規模為n，最大迭代次數為T，搜索空間維度為D。初始化過程中時間復雜度為O （ N ），標準DMO 算法中的時間復雜度為O （ N ×（ T × D + 1 ） ）。本文算法中，對種群初始化未進行改動，時間復雜度為O （ N ），針對算法迭代并未添加其他算式，僅對不同分類組別算法算式進行優化，并優化種群個體任務分配方法，故算法迭代期間時間復雜度為O （ T × N ×D ）。因此本文算法的時間復雜度為O （ N ×（ T × D +1 ） ），與標準DMO 的時間復雜度一致。

3 數值實驗仿真分析

3.1 仿真實驗環境與測試函數

實驗仿真測試環境為：64 位Windows 10 操作系統，處理器為AMD 2600X，主頻3.6 GHz，內存16 GB，仿真軟件為Matlab R2020b。

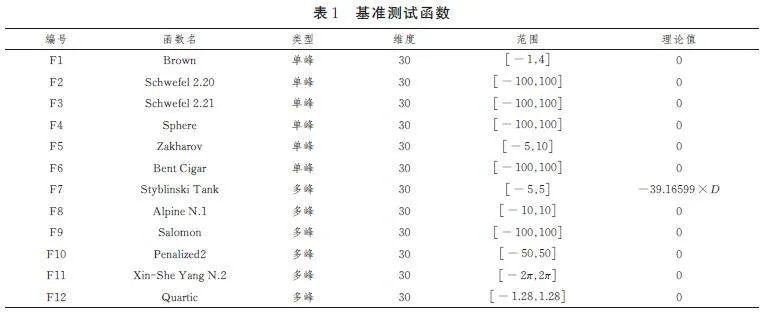
為了全面分析本文算法性能，與國內外學者對標準DMO 算法提出的改進算法BDMSAO［18］、IDMO［19］以及標準DMO［16］算法、海鷗優化算法（SOA）［10］、學生心理優化算法（SPBO）［12］進行仿真數值實驗分析，以此來具體分析本文算法與同類型改進之間的優劣差距及本文算法與其他優化算法之間優劣差距。本文選取了國內外學者常用的12 個經典基準測試函數作為本文算法的函數測試集，具體見表1。

3.2 數值實驗分析

為了公平性，所有對比算法均在同一實驗環境下進行數值實驗仿真。其中種群規模均設為30，算法最大迭代次數為500。其中DMO［16］ 、IDMO［19］ 、BDMSAO［18］、SPBO［12］、SOA［10］算法的參數設置均與相應文獻設置一致。

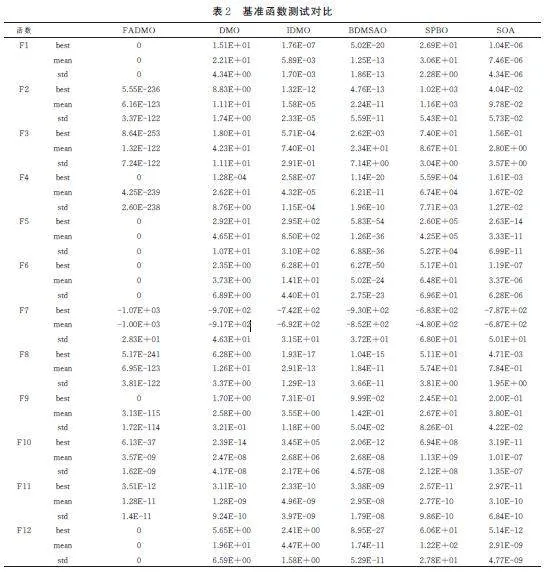
為了盡可能降低群智能優化算法自身隨機性對算法評價的影響，本文做數值實驗時，將本文算法與其他5 種算法針對每一基準測試函數均獨立進行了30次的測試實驗，并基于這30 次實驗所得結果，從中求出最優值（best）、平均值（mean）與標準差（std）3 個數據評價指標。這3 個評價指標在總體上反映了算法優化能力的強弱，其中：最優值指標反映了算法的尋優精度；平均值和標準差指標對應了算法的穩定性。六種算法分別求解表1 中的基準測試函數，其數值實驗分析結果在表2 中。

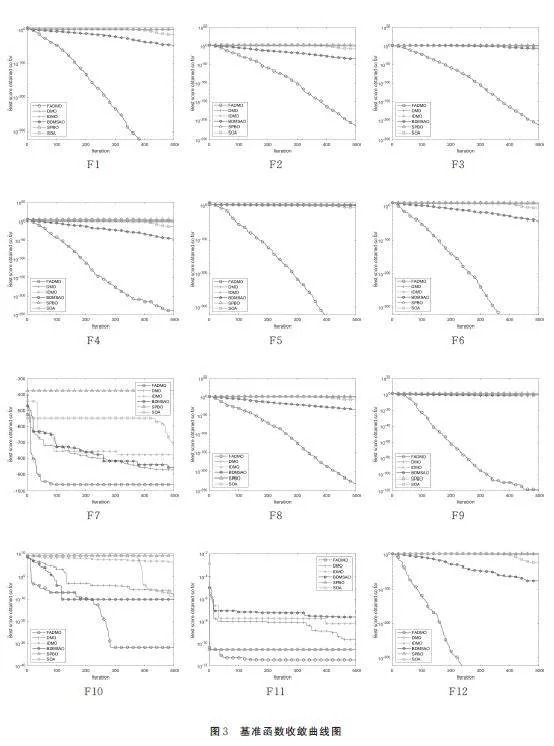
根據表2 實驗結果來比較六種算法各自的優化性能：1）本文算法在F1、F5、F6、F12 這4 個測試函數的最優值、平均值與標準差均為相應函數的理論最優值，這說明本文算法在求解這4 個函數時30 次獨立實驗均能找到其理論最優解，其余5 種算法求解這12 個基準測試函數均無法在30 次獨立實驗中找到對應函數的理論最優解。2）從最優值評價指標上看，在求解F4、F9 這2 個函數時，本文算法在30 次獨立實驗中有找到其理論最優解，其他算法求解F4、F9 這2 個函數時30 次獨立實驗均未能找到其理論最優解；求解F2、F3、F8 這3 個函數時尋優精度均比其余5 種算法提升230 個數量級以上；求解F7、F10、F11 這3 個函數時尋優精度均比其余5 種算法提升1 個數量級。3）從平均值與標準差評價指標上看，本文算法求解F2～F4、F8、F9 這5 個函數時尋優精度均比其余5 種算法提升100個數量級以上；求解F7、F10、F11 這3 個函數時尋優精度均比其余5 種算法提升1 個數量級。因此，本文算法在算法尋優精度與算法穩定性上相比其余5 種算法的提升程度非常明顯。

為了更直觀的比較6 種算法的收斂速度，本文給出6 種算法在求解表1 中基準測試函數的收斂曲線對比圖，具體見圖3。從圖3 中可以看出，本文算法在所有基準函數中的收斂曲線均在其他5 種對比算法收斂曲線的下方位置，因此本文算法對于所有基準函數的收斂效果均比其他5 種對比算法要好，本文算法的搜索速度是6 個算法中最快的。基于以上分析，說明了本文算法（FADMO）比其他5 種算法具有更快的全局收斂速度，更好的全局尋優精度，且優勢非常明顯。

3.3 求解不同規模下優化問題比較

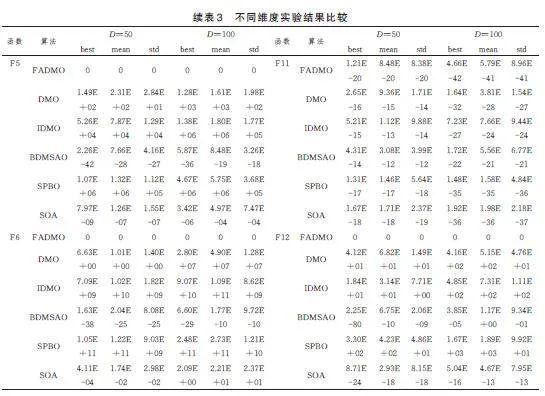
為了驗證本文算法在不同規模的優化問題時的性能，觀察算法是否會因為優化問題規模的增大而造成失靈現象出現，本文針對表1 中的12 個基準函數，分別取維度為50 和100 兩種情況。除維度外，數值實驗分析的其他參數與3.2 中設置完全一致。數值實驗分析結果詳情在表3 中。

依據表3 實驗結果分析6 種算法的性能。對于D=50 和100 兩種不同規模：1）本文算法在F1、F5、F6、F12 這4 個函數的3 個指標對應值仍為對應函數的理論最優值，表示隨維度增加本文算法在求解上述函數時性能未下降。其余5 種算法在求解12 個基準函數時，3 個指標對應值與D=30 相比均出現了數量級的下降，表示隨維度增加其他5 種算法尋優精度與穩定性均出現了下降。2）從最優值評價指標上看，本文算法求解F4、F9 這兩個函數時仍能找到其理論最優解，并未因維度增加造成算法尋優能力下降；求解F2、F3、F8、F10 這4 個函數時找到的最優值與D=30 時量級相當，沒有因維度增加出現失靈現象，其他5 種優化算法在求解12 個基準函數時，隨著維度的增加，最優值尋優精度均出現了下降；求解F7 時因測試函數自身理論最優值隨維度變化而變小，故可以觀察到D=50 和100 時尋優值逐漸更小，但本章算法求解適應度值在六種算法中仍為最優；求解F11 時6 種算法求解精度均隨維度增大尋優能力增強，對比D=30、50 和100 可以發現本文算法提升幅度最為明顯。3）從平均值與標準差評價指標上看，本文算法求解F2～F4、F8～F10這6 個測試函數的對應結果相比D=30 時收斂精度略有下降，但較其他5 種算法，下降幅度更小，性能最優；本文算法求解F7 時仍優于其他5 種算法；求解F11 時優于其他5 種算法并收斂精度提升數量級高于其他五種算法。基于以上分析，相比于其他5 種算法，本文算法不會隨維度規模增大而影響其尋優精度，求解較大規模優化問題時，仍表現出較好的優化性能和算法穩定性。

3.4 FADMO 解決SVM 參數調優問題

支持向量機（SVM）作為一種基于統計學理論的新型機器學習方法，因其具有很好的泛化性能，并在處理高維數據集時具有一定的優勢，在文本分類、圖像識別等方向得到了廣泛的應用。本章使用FADMO算法解決SVM 參數調優問題，分類器采用C-SVC。該分類算法共涉及到兩個重要參數：懲罰系數C、RBF 核函數寬度參數σ，可知問題維度為2。本章內容中取C ∈ [ 0.01，35000 ]，σ ∈ [ 0.01，100 ]。SVM 參數調優目的，是為了提升模型在測試集中的準確率，故準確率越高則參數選擇越適宜。為與本論文上述測試函數中適應度值越低越優相一致，本章節設置SVM 參數調優問題適應度函數定義公式（10），適應度值越低則表示參數選擇越適宜，模型準確率越高。

其中，Nacc 為測試集中分類正確的樣本數量，Nall 為測試集中總樣本數量。

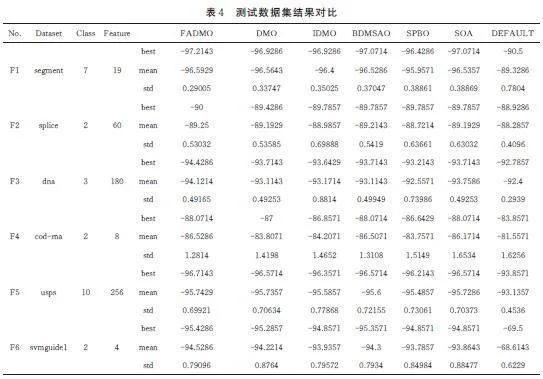
為了全面分析FADMO 算法求解SVM 參數調優問題性能，本文仿真中，種群規模均設為30，算法最大迭代次數為100。數據集預處理中，統一設置訓練集為700 個數據樣本，測試集為1400 個數據樣本，且均為從測試數據集中隨機選擇，訓練集與測試集均無相同樣本。將本文算法與DMO［16］、IDMO［19］、BDMSAO［18］、SPBO［12］、SOA［10］5 種算法及默認SVM 參數設置（C =1，σ = 1/k，其中k 為特征數量）對測試數據集進行仿真數值實驗分析，實驗環境及對比算法與3.2 一致。為了降低隨機性對算法評價的影響，針對每一測試數據集，每種算法均獨立進行10 次實驗，且每次實驗均隨機生成一次訓練集與測試集。基于這10 次實驗所得結果，從中求出最優值、平均值與標準差3 個數據作為算法評價指標。數據集相關信息及數值實驗結果見表4。

根據表4 實驗結果來比較6 種算法各自的優化性能：1）從最優值與平均值指標上看，FADMO 算法求解6 個測試數據集的準確率均優于默認參數。2）從最優值評價指標上看，FADMO 算法求解F1～F3、F5、F6這5 個測試數據集時求解精度優于其他5 種算法，在求解F4 這個測試數據集時求解精度與BDMSAO、SOA 兩算法并列最優。3）從平均值與標準差評價指標上看，FADMO 在F1～F6 這6 個測試數據集中10 次求解下平均準確率均高于其他5 種優化算法，且標準差均低于其他5 種優化算法。因此，FADMO 在SVM 參數調優問題中算法尋優精度、算法適用性、算法穩定性相比其余5 種算法的提升效果非常明顯。

綜合上述分析，本文算法通過與其他5 種算法對6個經典測試數據集進行數值實驗，驗證了FADMO 在解決支持向量機參數調優問題時擁有較強的優化能力，適用范圍較為廣泛。

4 結語

本文針對標準DMO 的不足，提出基于覓食能力分配搜索任務的侏儒貓鼬優化算法（FADMO）：使用tent 混沌自適應步長，利用tent 混沌映射的波動性，提升了種群搜索的多樣性；利用當前全局最優位置為指引，以alpha 組隨機個體為擾動，解決alpha 組個體覓食行為過于盲目的問題，增強了算法的全局尋優能力；優化偵查組搜索模型，進一步提升偵查組個體定向開發能力；提出讓保姆組承擔局部開發任務，增強了算法的局部搜索能力；提出一種新的種群內個體任務分配方法，提升算法整體收斂性能與收斂速度。通過基準測試函數數值實驗，驗證了本文算法的收斂性能與尋優能力。將本文算法應用于解決支持向量機參數調優問題，驗證了本文算法具有實際問題求解能力與實用性。在后續研究中，考慮將本文算法與機器學習、深度學習等進行結合應用。

［參考文獻］

[1] ABDEL-BASSET M， CHANG V， MOHAMED R. HS?MA_WOA： A hybrid novel Slime mould algorithm with whale optimization algorithm for tackling the image segmenta?tion problem of chest X-ray images[J]. Applied soft comput?ing， 2020， 95： 106642.

[2] 呂鑫，慕曉冬，張鈞，等. 混沌麻雀搜索優化算法[J]. 北京航空航天大學學報，2021，47（8）：1712-1720.

[3] DENG W， XU J， ZHAO H. An improved ant colony optimi?zation algorithm based on hybrid strategies for scheduling problem[J]. IEEE Access， 2019， 7： 20281-20292.

[4] 路雪剛，張雪花，張夢桃. 基于改進鯨魚優化算法的畜禽廢棄物運輸路徑優化問題[J]. 科學技術與工程， 2022， 22（25）：11120-11129.

[5] HEKIMO?LU B. Optimal tuning of fractional order PID con?troller for DC motor speed control via chaotic atom search op?timization algorithm[J]. IEEE Access， 2019， 7： 38100-38114.

[6] QI Z， SHI Q， ZHANG H. Tuning of digital PID controllers using particle swarm optimization algorithm for a CAN-based DC motor subject to stochastic delays[J]. IEEE Transactions on Industrial Electronics， 2019， 67（7）： 5637-5646.

[7] DHIMAN G， KUMAR V. Seagull optimization algorithm：Theory and its applications for large-scale industrial engineer?ing problems[J]. Knowledge-based systems， 2019， 165：169-196.

[8] XUE J， SHEN B. A novel swarm intelligence optimization approach： sparrow search algorithm[J]. Systems Science amp;Control Engineering， 2020， 8（1）： 22-34.

[9] DAS B， MUKHERJEE V， DAS D. Student psychology based optimization algorithm： A new population based optimi?zation algorithm for solving optimization problems[J]. Advanc?es in Engineering software， 2020， 146： 102804.

[10] HAYYOLALAM V， KAZEM A A P. Black widow optimi?zation algorithm： a novel meta-heuristic approach for solving engineering optimization problems[J]. Engineering Applica?tions of Artificial Intelligence， 2020， 87： 103249.

[11] ABUALIGAH L， DIABAT A， MIRJALILI S， et al. The arithmetic optimization algorithm[J]. Computer methods in applied mechanics and engineering， 2021， 376： 113609.

[12] ABUALIGAH L， YOUSRI D， ELAZIZ MABD， et al.Aquila optimizer： a novel meta-heuristic optimization algo?rithm[J]. Computers amp; Industrial Engineering， 2021， 157：107250.

[13] 張偉，王勇，張寧. 采用混合策略的改進學生心理優化算法[J]. 計算機應用研究，2022，39（6）：1718-1724.

[14] 張喆，張義民，張凱，等. 基于拉格朗日插值的教與學動態組自適應算法[J]. 計算機工程與設計， 2022， 43（10）： 2813-2821.

[15] 許樂，莫愿斌，盧彥越. 具有記憶功能的海鷗優化算法求解方程組[J]. 計算機工程與設計，2021，42（12）：3428-3437.

[16] AGUSHAKA J O， EZUGWU A E， ABUALIGAH L.Dwarf mongoose optimization algorithm[J]. Computer meth?ods in applied mechanics and engineering， 2022， 391：114570.

[17] ELAZIZ M A， EWEES A A， AL-QANESS M A A， et al. Feature Selection for High Dimensional Datasets Based on Quantum-Based Dwarf Mongoose Optimization[J]. Math?ematics， 2022， 10（23）： 4565.

[18] AKINOLA O A， EZUGWU A E， OYELADE O N， et al.A hybrid binary dwarf mongoose optimization algorithm with simulated annealing for feature selection on high dimensional multi-class datasets[J]. Scientific Reports， 2022， 12（1）：1-22.

[19] 賈鶴鳴，陳麗珍，力尚龍，等. 透鏡成像反向學習的精英池侏儒貓鼬優化算法[J/OL]. 計算機工程與應用：1-12[2023-04-14].http：∥kns.cnki.net/kcms/detail/11.2127.TP.20221019.1554.014.html.

[20] AGUSHAKA J O， AKINOLA O， EZUGWU A E， et al.Advanced dwarf mongoose optimization for solving CEC 2011 and CEC 2017 enchmark problems[J]. Plos one，2022， 17（11）： e0275346.

[21] 趙世杰，張紅易，馬世林. 領導者引導與支配解進化的多目標矮貓鼬算法[J/OL]. 計算機科學與探索：1-22[2023-04-14].http：∥kns.cnki.net/kcms/detail/11.5602.TP.20221213.1733.002.html.

［責任編輯 蘇琴］