一道高考多選題的深度教學與思考*

劉 娟

?合肥市第一中學合肥市劉娟教育名師工作室

自2020年起，全國高考數學新課標Ⅰ卷以《普通高中數學課程標準(2017年版)》和《中國高考評價體系》為依據，試卷不分文理科，由八道單項選擇題、四道多項選擇題、四道填空題和六道必做解答題組成.其中，多項選擇題是新的類型，每小題5分，部分選對得2分，有選錯得0分，即見錯歸零，減少單選題中通過盲選也可得滿分的可能性，有效提高了滿分的思維價值.多選題的構成要素較復雜，破解難度大，需要的能力點多，依托數學模型，強調對數學思想方法的考查，要求學生具有完備、細致、全面的思維品質[1].多選題四題中前兩題較為基礎，后兩題難度較大.

筆者以2021年新課標Ⅰ卷第12題為例，分析問題并從深度學習的不同角度給出教學建議.

1 問題呈現

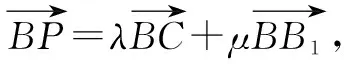
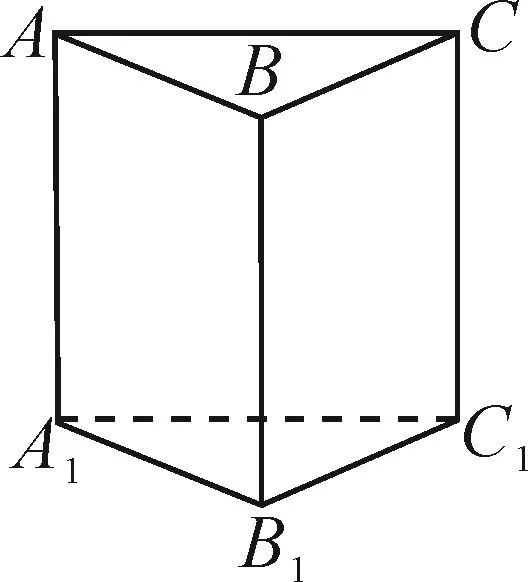
圖1

A.當λ=1時，△AB1P的周長為定值

B.當μ=1時，三棱錐P-A1BC的體積為定值

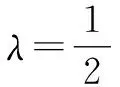
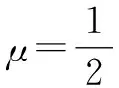
2 問題破解

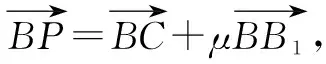
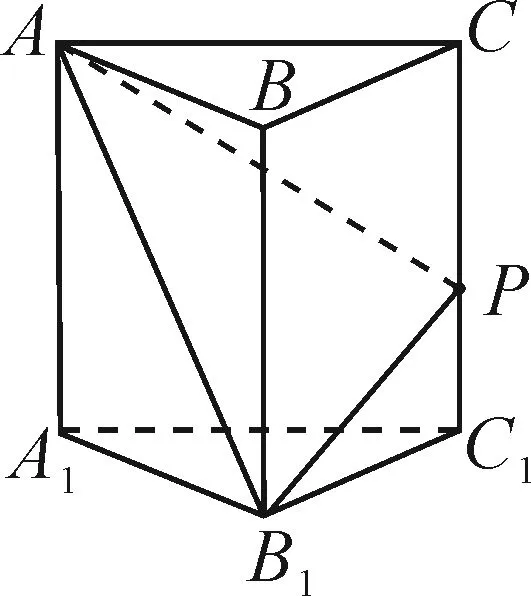
圖2

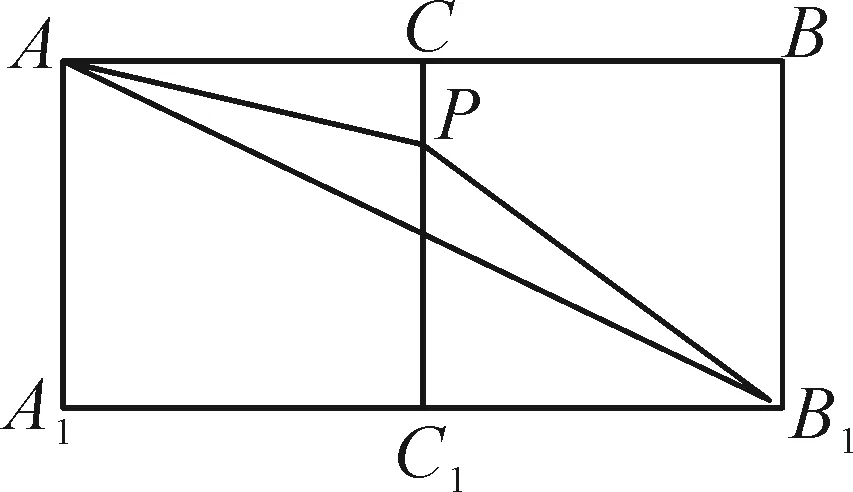
圖3

法1：計算點P分別在線段CC1的端點C，C1及在線段CC1中點處時△AB1P的周長，對應的△AB1P的周長不相等，從而△AB1P的周長不是定值，故排除A選項.

法2：如圖3，將面AA1C1C與面BCC1B1展開成長方形AA1B1B，連結AB1，由于點P在線段CC1上運動，顯然△AB1P的周長不是定值.

法3：要判斷△AB1P的周長是否為定值，只需判斷|B1P|+|PA|是否為定值.

設|PC1|=x，x∈[0，1]，則

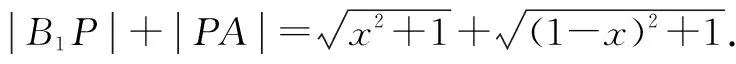
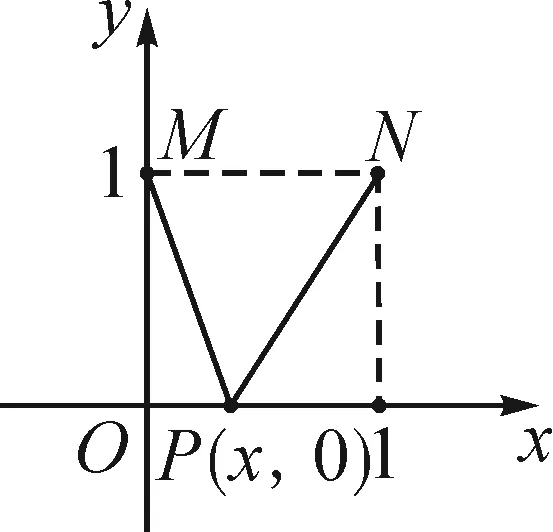
圖4

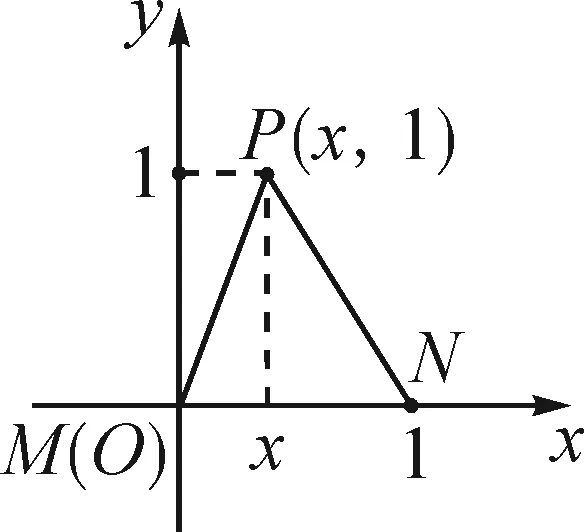
圖5

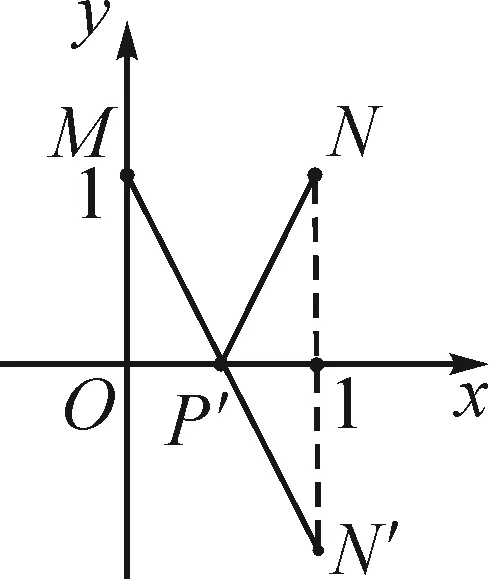
圖6

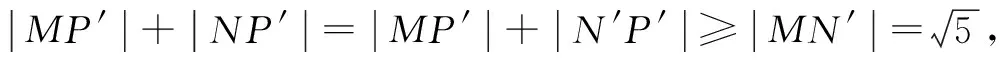
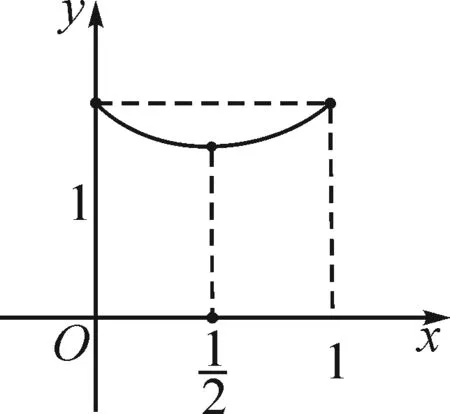
圖7

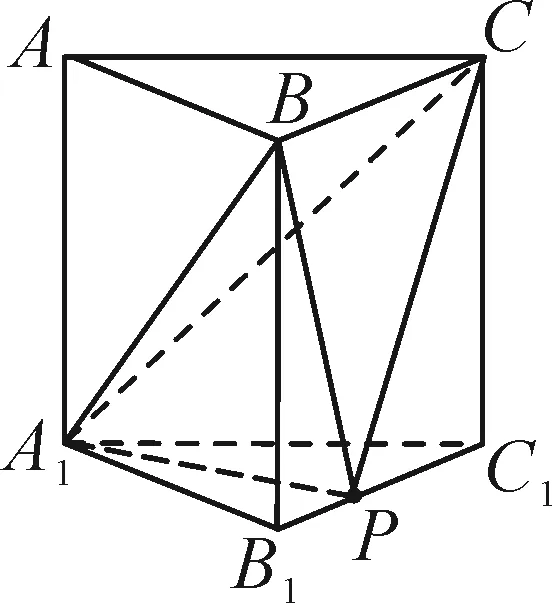
圖8

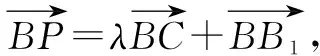
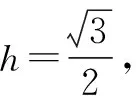
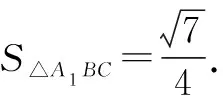
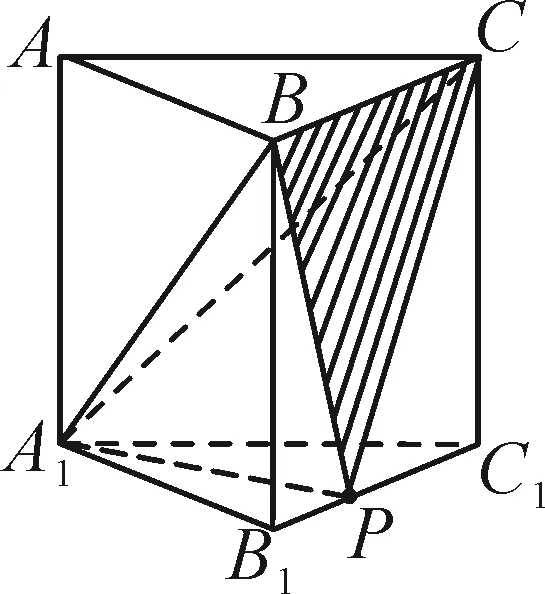
圖9

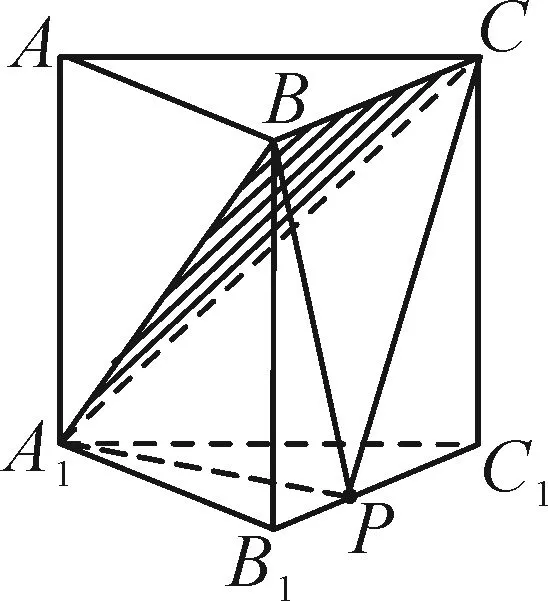
圖10

圖11

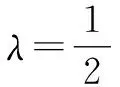
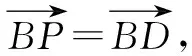
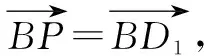
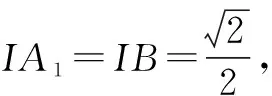
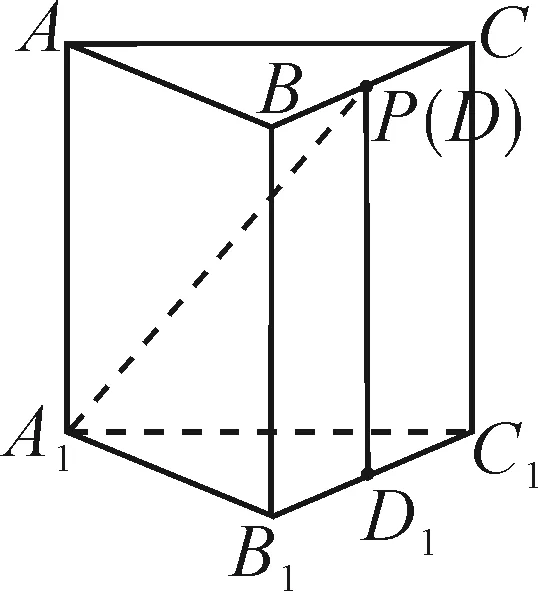
圖12

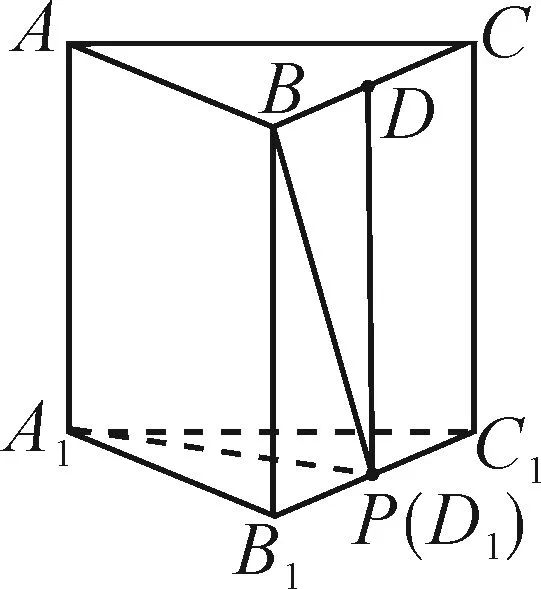
圖13

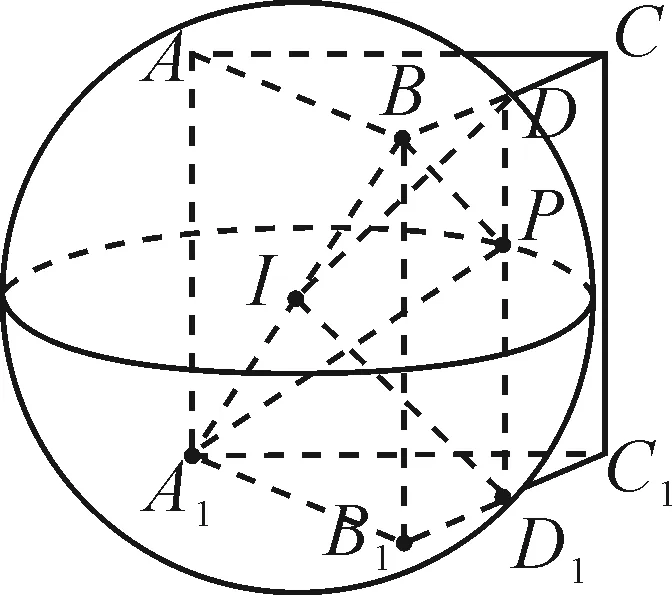
圖14

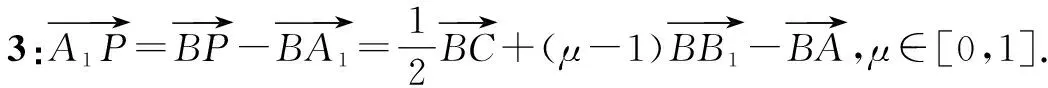
所以μ=0或μ=1.故點P不唯一.

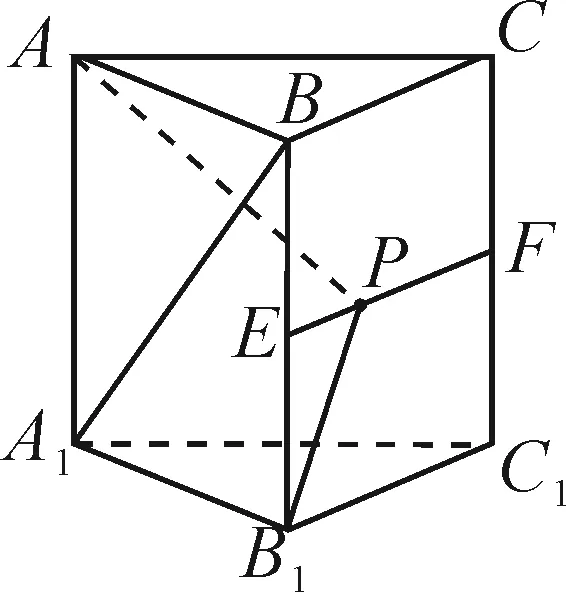
圖15

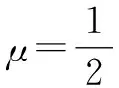
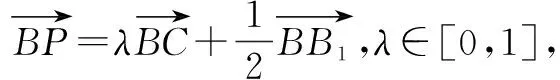
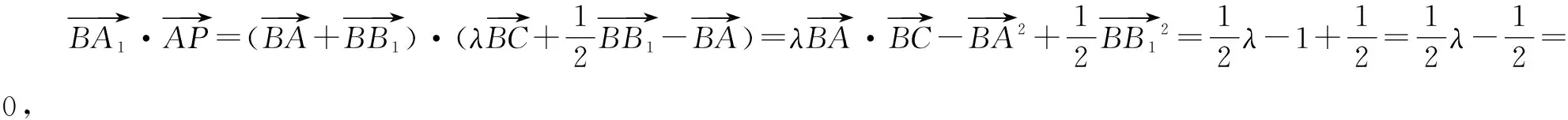
故有且只有一個點P滿足條件.

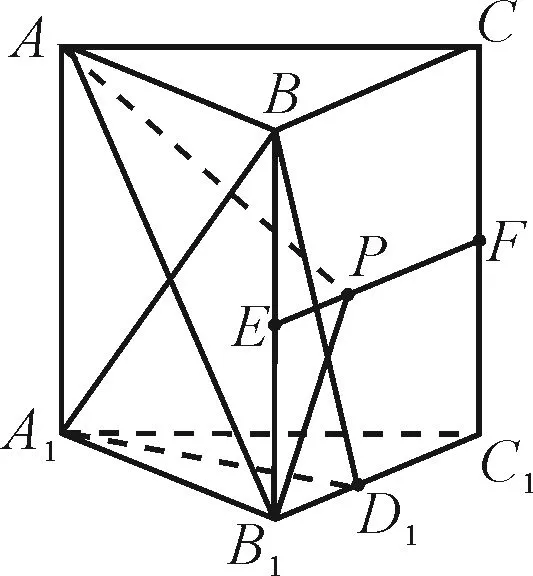
圖16

法2：要證A1B⊥平面AB1P，只需證明A1B垂直于平面AB1P內的兩條相交直線.由于ABC-A1B1C1是正三棱柱，顯然A1B⊥AB1.問題轉化為“判斷滿足A1B⊥B1P的點P是否唯一”.點A1在平面BCC1B1內的投影為B1C1的中點D1(如圖16)，要想得出A1B⊥B1P，只需證BD1⊥B1P成立即可.顯然只有當點P運動到點F時，△BB1D1≌△B1C1F，易得BD1⊥B1P，從而A1B⊥B1P.因此有且僅有一個點P，使得A1B⊥平面AB1P.故選項D正確.

研究圖形的基本思想方法有綜合幾何法、解析幾何法、向量幾何法和分析法.在上述討論中，顯然向量幾何法在位置關系的判斷上比較簡潔，后兩個選項直接利用平面向量的數量積便可做出判斷，但在度量關系上并不一定占據優勢，所以前兩個選項重點用綜合幾何法和分析法進行判斷.本題還可以通過建立空間直角坐標系，使用空間向量的坐標運算來研究圖形，具體解法交由讀者自行研究.

3 教學建議

3.1 關注研究內容的結構與聯想

本題對圖形的基本性質(如圖17所示)的考查全面且深入.題干運用平面向量基本定理表述點的位置，利用系數的變換，點動成線，用平面的表述方式實現空間位置的確定，體現了立體幾何教學中常用的將三維空間幾何問題轉化為二維平面中的問題來解決的基本思想.《普通高中數學課程標準(2017年版2020修訂)》對整體的課程架構歸納為整體→局部→整體，其中運動變化觀點是幾何課程的主線之一，而從變化中抓住不變的本質是教學的重難點.關注學生的思維過程，講解的思維進階要符合學生的認知規律.隨著內容的遞進，以立體幾何為主體，不斷聚合不同主題下的相關知識點，抽絲剝繭，再重新織成網，以此為觸發器帶動學生由被動學習到學會思考、學會遷移.

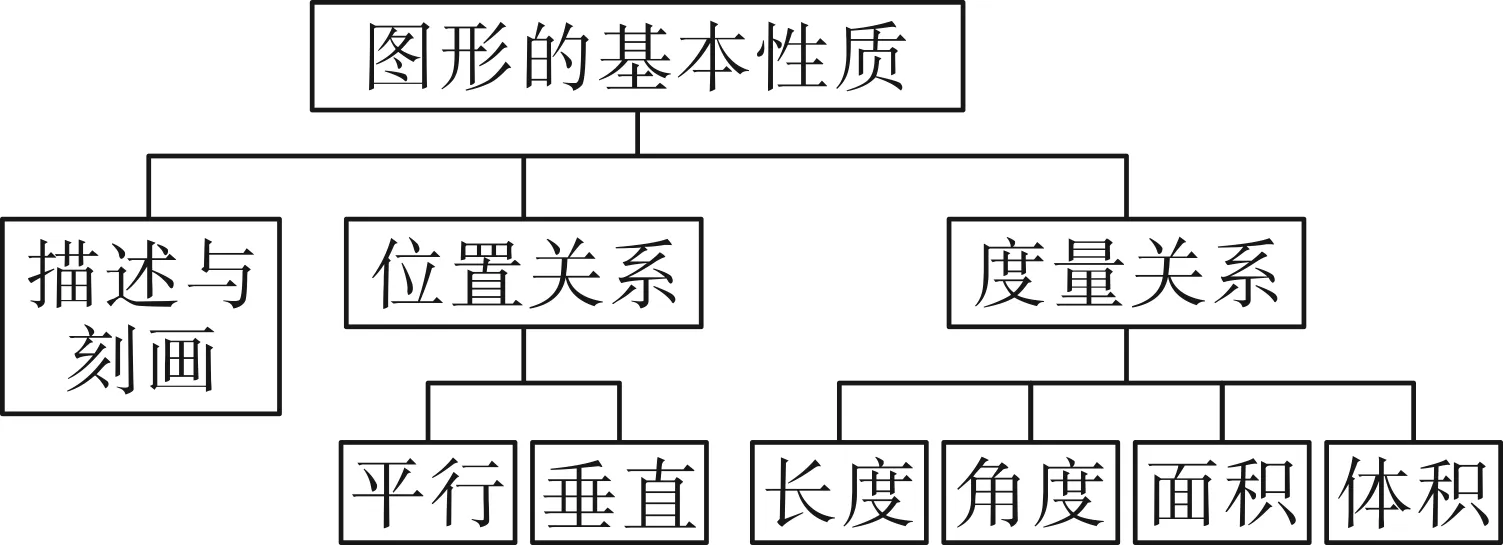
圖17

3.2 拓展軌跡形式，內化知識的本質

本題四個選項得出的點P的軌跡僅為與三棱柱的棱平行或垂直的線段，還可以作出以下變式，可不拘泥于題中λ，μ的范圍.本質與變式強調的是學生對教學內容的內化[2].

變式1點P的軌跡為在三棱柱側面或底面上的線段.

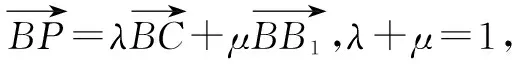
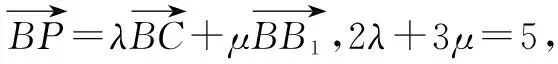
變式2點P的軌跡為在三棱柱側面或底面上的曲線.

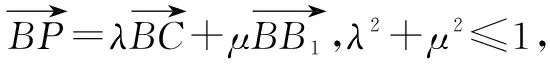
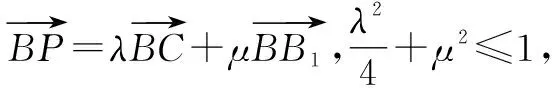
變式3點P的軌跡為在三棱柱內的平面或曲面.

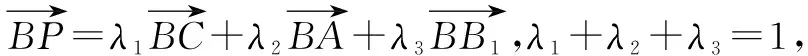
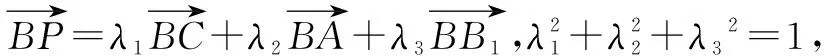
3.3 重要特征一般化，實現知識的遷移

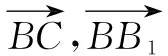
以正三棱柱為載體體現了新高考考查主干內容的基礎性，強調了利用模型解題的通性通法，也可以回歸到最基本的正方體中，還可以在夯實點線面位置關系的同時強化度量關系，尤其是本例中未強調的角度問題，也可以通過割補等方式，引入陌生幾何體，或者加強對生活實踐的考查，以現有建筑或生活用品呈現的幾何體為例抽象出空間圖形，以生考熟.

學會應用是遷移的重要表征，也是檢驗學習效果的最佳途徑.遷移與應用強調的是學生對學習成果的外化.如果把學習過程看作一個閉環結構，那么遷移發生在閉合處，從別處遷移來，又從這里遷移到別處[2].

4 深度學習的發生

深度學習具有在學習對象(內容)上關注聯想與結構、本質與變式，在學習機制中關注活動與體驗、在學習實踐中關注遷移與應用，以及關注學生核心素養發展的價值與評價等特征[3].

高考立足于立德樹人根本目標，目前是新課標、新課程、新教材與新高考的交匯時期，如何以核心知識的講授、核心素養的培養為不變，應命題方式、試卷結構及題目類型等的萬變，教師需要思考并嘗試，堅持結合學生的切身實際，持續改進教學.研究高中數學深度學習后發現，思維的深度很多時候體現在數學思想方法的運用上，當學生能夠結合數學思想方法建立起能遷移且具有批判精神的思維方式時，深度學習就能夠成為發生在課堂中的真實景象[4].