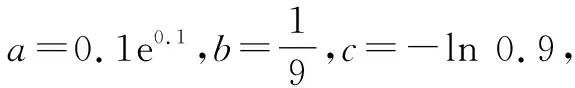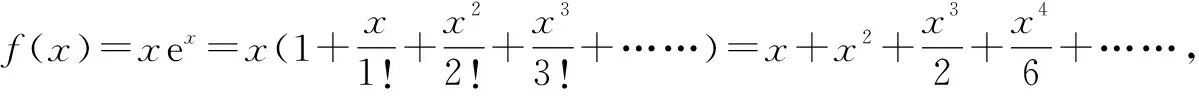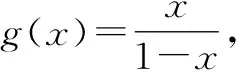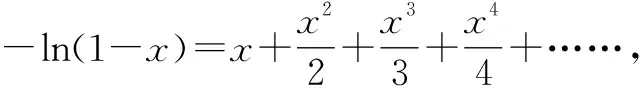結合2022年高考談高三數學復習
張永兵
?甘肅省白銀市第九中學
為高效地進行高三數學復習,實現有效教學,讓數學核心素養走進課堂,厘清深度學習邏輯的核心意蘊,筆者結合2022年高考數學試題從夯實基礎知識、滲透數學文化、加強綜合應用、巧用高觀點結論四個方面對高三數學復習進行探討.
1 夯實基礎知識
高三數學復習應該在深度理解概念的基礎上,發展數學抽象、邏輯推理等核心素養.對稱軸或對稱中心問題往往條件比較隱蔽,通常根據已知條件進行恰當地轉化,得到所需的一些數值或關系式進而解題.
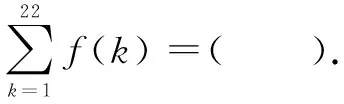
A.-21 B.-22 C.-23 D.-24
解:因為y=g(x)的圖象關于直線x=2對稱,所以g(2-x)=g(x+2).
因為g(x)-f(x-4)=7,所以g(x+2)-f(x-2)=7,即g(x+2)=7+f(x-2).
因為f(x)+g(2-x)=5,所以f(x)+g(x+2)=5,則f(x)+7+f(x-2)=5,即f(x)+f(x-2)=-2.
故f(3)+f(5)+……+f(21)=(-2)×5=-10,
f(4)+f(6)+……+f(22)=(-2)×5=-10.
因為f(x)+g(2-x)=5,所以f(0)+g(2)=5,即f(0)=1,故f(2)=-2-f(0)=-3.
因為g(x)-f(x-4)=7,所以g(x+4)-f(x)=7.又f(x)+g(2-x)=5,故g(2-x)+g(x+4)=12,則y=g(x)的圖象關于點(3,6)中心對稱.
因為函數g(x)的定義域為R,所以g(3)=6.又f(x)+g(x+2)=5,于是f(1)=5-g(3)=-1.
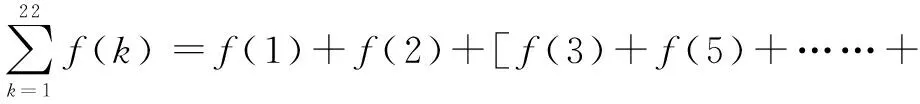
復習總結:函數奇偶性與對稱性之間的關系.
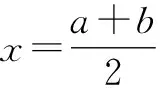
(2)若函數y=f(x+a)是奇函數,即f(-x+a)=-f(x+a)恒成立,則函數y=f(x)關于點(a,0)中心對稱;一般地,若對于R上的任意x都有f(a+x)+f(a-x)=2b恒成立,則y=f(x)的圖象關于點(a,b)對稱.
(3)若函數有多重對稱性,則該函數具有周期性且最小正周期為相鄰對稱軸距離的2倍,為相鄰對稱中心距離的2倍,為對稱軸與其相鄰對稱中心距離的4倍.(注:如果遇到抽象函數給出類似性質,可以聯想y=sinx,y=cosx的對稱軸、對稱中心和周期之間的關系.)
善于發現函數的對稱性(中心對稱、軸對稱),有時需將函數得對稱性與奇偶性相互轉化.
2 滲透數學文化
在高三復習中要特別注意數學文化的滲透.高考試題往往通過創設情境,改變設問方式,將數學史、數學美、數學精神與數學知識有機結合,改變以往單純的知識性考查,體現了數學文化本身對于數學教育與數學學習的重要意義,充分發揮高考命題的育人功能和積極的導向作用.
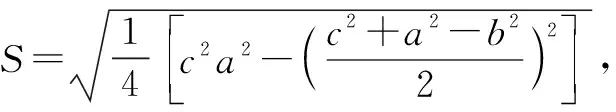
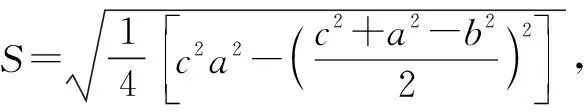
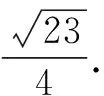
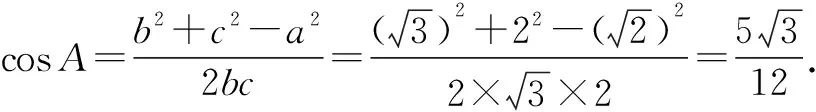
復習啟示:挖掘教材中的數學文化資源.如必修3中秦九韶算法,更相減損術;選修4-5中伯努利不等式,教材習題中的阿波羅尼圓、高斯函數,教材閱讀與思考中的祖暅原理、斐波那契數列.賞析歷年數學文化名題,通過創設新穎的文化背景,在新的背景中掌握并應用數學知識,發揮數學文化的育人價值,促進學生理性思維的發展.
3 加強綜合應用
數學知識的綜合應用是數學價值的體現.比如,比較大小是指數函數、對數函數、冪函數的重要考點.當底數相同,構造指數函數或對數函數,利用函數單調性或圖象來解決;當不同底數不同指數或指對混合比較時,可以找中間量-1,0,1等.
例3(2020年全國Ⅰ卷第12題)若2a+log2a=4b+2log4b,則( ).
A.a>2bB.a<2bC.a>b2D.a 解:設f(x)=2x+log2x,則f(x)為增函數. 所以f(a) f(a)-f(b2)=2a+log2a-(2b2+log2b2)=22b+log2b-(2b2+log2b2)=22b-2b2-log2b. 故當b=1時,f(a)-f(b2)=2>0,即f(a)>f(b2),則a>b2. 當b=2時,f(a)-f(b2)=-1<0,即f(a) 復習突破:高考數學復習在制高點上就是數學應用,是知識能力的遷移、思維品質的發展[1].數學知識只有深度應用,才能實現知識點之間的貫通和轉換,這樣學生才能深刻領會知識中所蘊含的數學思想和方法,使得新型題變成了“舊”問題、“舊”知識,減少了學生對陌生問題的恐懼感,達到“一把鑰匙開多把鎖”的目的,從而使復習更高效. 在高三復習中滲透高觀點的數學思想方法,有助于拓展解題思路,認清某些初等數學問題的實質.如以拉格朗日中值定理、泰勒展開式為背景設計的高考題,把初等函數與超越函數有機聯系起來,通過高考題展示高觀點對中學數學的意義. A.a C.c 顯然c 復習心得:開展“高觀點”下的中學數學研究能夠促進數學教師專業化成長,有助于提升校本教材的開發,有助于培養學生的探究性學習能力和創新精神.
4 巧用高觀點結論